Video Lecture
Theory For Making Notes
Thermal Expansion
When matter is heated without any change in it’s state, it usually expands (Except few . Solids can expand in one dimension (linear expansion), two dimension (superficial expansion) and three dimension (volume expansion) while liquids and gases usually suffers change in volume only.Hence there are three types of thermal expansion
1.
Linear expansion
2.
Superficial expansion
3.
Volumetric expansion
Linear expansion

Consider a linear object of length l at a temperature t1.Now it is heated through a small temperature dtas a result the fractional change in length (dl/l) is directly proportional to change in temperature `dt’
so \frac{{d\,l}}{l}\propto dt
in place of proportionality sign we put a constant a.wherea is known as the thermal coefficient of linear expansion and it depends on the material of the rod.
therefore \frac{{d\,l}}{l}=\alpha dt.
\frac{{d\,l}}{l}=\alpha dt
\Rightarrow dl=l\alpha dtFor a small change in temperature we can integrate dl to get final length after heating.
\Rightarrow \int\limits_{{{{l}_{{}}}}}^{L}{{dl}}=l\alpha \int\limits_{{{{t}_{1}}}}^{{{{t}_{2}}}}{{dt}}
\Rightarrow L-l=l\alpha ({{t}_{2}}-{{t}_{1}})
hence \Rightarrow L=l[1+\alpha ({{t}_{2}}-{{t}_{1}})] or L=l[1+\alpha \Delta t]
here we have assumed that change in length varies linearly with change in temperature and the change in length is also very small .But it happens only for a small change in temperature. The graph between the length `L’ and \Delta t is a straight line as shown below
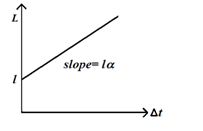
Similar expressions can be written for change in area for a two-dimensional object and change in volume for a three dimensional object.
S = S0 (1 + βΔt ) \Rightarrow \Delta S=\beta {{S}_{o}}\,\Delta t
& V = V0 (1 + γΔt) \Rightarrow \Delta V=\gamma {{V}_{o}}\,\Delta t
whereb and gare coefficients of superficial expansion and coefficient of cubical expansion respectively.
The relation between a, β and γ for an isotropic solid is a : β : γ = 1 : 2 : 3.
The three coefficients of expansion are not constant for a given solid. Their values depend on the temperature range in which they are measured. The values of a , β , γ are independent of the units of length, area and volume respectively.
For anisotropic solids \gamma ={{\alpha }_{x}}+{{\alpha }_{y}}+{{\alpha }_{z}} where ax, ay, and azrepresent the mean coefficients of linear expansion along three mutually perpendicular directions.
(For the derivation of relation between a, b and g please watch the video lectures)
Thermal Stress
When a rod is held between two fixed supports and its temperature is increased, the fixed supports do not allow the rod to expand, which results in a stress, which is called thermal stress.
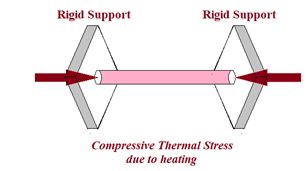
Let a rod of length l is held between two fixed supports and its temperature is increased by ΔT, then change in length of the rod
Δl = laΔT
where a is thermal coefficient of linear expansion for the material of the rod.
If Y is the Young’s modulus for the material of the rod and A is the area of cross-section of the rod then mechanical compression in the rod.
Δl’ = \left( {\frac{F}{A}} \right)\,\,\frac{l}{Y}
Since support is rigid Δ l + Δl’ = 0, which gives \frac{F}{A}\,=\,-\,\alpha \,Y\Delta T
This is thermal stress, – ve sign indicates that thermal stress is compressive in nature.
Some other examples of Thermal Expansion in Solids
(1) Bi-metallic strip
(2) Effect of temperature on the time period of a simple pendulum
(3) Error in scale reading due to expansion or contraction
(5) Expansion of cavity
(6) When rails are laid down on the ground, space is left between the ends of two rails.
(7) The transmission cable are not tightly fixed to the poles.
(8) Test tubes, beakers and crucibles are made of pyrex-glass or silica because they have very low value of coefficient of linear expansion.
(9) The iron rim to be put on a cart wheel is always of slightly smaller diameter than that of wheel.
For detailed explanation of first five examples, watch the video lectures
Expansion of liquids
Liquids like solids expand on heating. The liquids have no definite shape and they experience volume expansion only. As the liquid is contained in a vessel, the observed expansion of liquid is less than the real expansion, because the capacity of vessel containing liquid increases with temperature. If {{\gamma }_{r}} is the coefficient of real expansion of liquid and {{\gamma }_{a}} the coefficient of apparent expansion of liquid and {{\gamma }_{g}} coefficient of volume expansion of solid container then
{{\gamma }_{r}}={{\gamma }_{a}}+{{\gamma }_{g}}
Variation of Density with Temperature
Most substances (solid and liquid) expand when they are heated, i.e., volume of a given mass of a substance increases on heating, so the density should decrease \left( {\text{as }\rho =\frac{m}{V}} \right) ( where m is mass ).
Let the density be \rho at temperature t1 and \rho ‘ at temperature t2. Then \displaystyle \rho =\frac{m}{V} and \displaystyle \rho ‘=\frac{m}{{V’}}
Þ \frac{{{\rho }’}}{\rho }=\frac{V}{{{V}’}}=\frac{V}{{V+\Delta V}}=\frac{V}{{V+\gamma V\Delta t}}=\frac{1}{{1+\gamma \,\Delta t}}
Þ {\rho }’=\frac{\rho }{{1+\gamma \,\Delta t}}
If \gamma \,\Delta tis very small binomial approximation can be used
So \rho ‘=\rho \,{{(1+\gamma \,\Delta t)}^{{-1}}}
hence \rho ‘=\rho \,(1-\gamma \,\Delta t) so with increase in temperature the density decreases.
Illustration
The design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and copper rod laid side by side at all temperatures. Find their lengths.
(αFe = 11 × 10–6 C–1, αCu = 17 × 10–6 °C–1)
Solution
Since the αCU>αFe so, length of iron rod should be greater than the length of copper rod.
Let the initial lengths of iron and copper rods be l1 and l2 , then
l1 –l2 = 10 cm … (i)
also since the difference has to be constant at all the temperatures, so
Δl = l1αFeΔT = l2αCuΔT
\frac{{{{l}_{1}}}}{{{{l}_{2}}}}\,=\,\frac{{{{\alpha }_{{Cu}}}}}{{{{\alpha }_{{Fe}}}}} … (ii)
Solving (i) & (ii) we get l1 =28.3 cm and l2 = 18.3 cm
Illustration
The height of mercury column measured at t°C with a brass scale which gives correct reading H1 at 0°C. What height H0 will the mercury column have at 0°C? The coefficient of linear expansion of brass is α and the coefficient of volume expansion of mercury is g.
Solution
H1 at t°C = H1 (1 + αt) actually since pressure is same, so
ρ0gH0 = ρtgH1 (1 + αt)
H0 = H1 (1 + αt) \frac{{{{\rho }_{t}}}}{{{{\rho }_{0}}}} = H1 (1 + αt) (1 + gt)–1
H0 = H1 [1 + (α- g) t]
Illustration
A sphere of diameter 7.0 cm and mass 266.5 g floats in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of 35°C. If the density of the liquid is 1.527 g/cm3 at 0°C, find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere.
Solution
It is given that the expansion of the sphere is negligible as compared to the expansion of the liquid. At 0°C, the density of the liquid is ρ0 = 1.527 g/cm3. At 35°C, the density of the liquid equals the density of the sphere. Thus,
{{\rho }_{{35}}}\,=\,\frac{{266.5\,g}}{{\frac{4}{3}\,\pi \,{{{(3.5\,cm)}}^{3}}}} = 1.484 g/cm3
We have \frac{{{{\rho }_{\theta }}}}{{{{\rho }_{0}}}}\,=\,\frac{{{{V}_{0}}}}{{{{V}_{\theta }}}}\,=\,\frac{1}{{(1+\gamma \theta )}}
or, ρq = \frac{{{{\rho }_{0}}}}{{1+\gamma \theta }}
Thus, g = \frac{{{{\rho }_{0}}-{{\rho }_{{35}}}}}{{{{\rho }_{{35}}}\,(35{}^\circ C)}} = \frac{{(1.527\,-\,1.484)\,g\,/c{{m}^{3}}}}{{(1.484\,\,g/c{{m}^{3}})\,\,(35{}^\circ C)}} = 8.28 × 10–4 /°C.
Illustration
The lengths l1i = 100 m of iron wire and l1c = 100 m of copper wire are marked off at t1 = 20 oC. What is the difference in lengths of the wires at t2 = 60 oC? The coefficients of linear expansion for iron and copper are ái = 1.2 x 10-5K-1and ác = 1.7 x 10-5 K-1.
Solution
l1i = loi(1 + áit1) and l2i = loi(1 + áit2)
The elongation of the iron wires is
l2i – l1i =loiái(t2 – t1).
Substituting loi = l1i/(1 + áit1), we find the elongation of the iron and copper wires
l2i – l1i = l1iái(t2 – t1)/(1 + áit1) (1)
l2c – l1c = l1các(t2 – t1)/(1 + áct1) (2)
Subtracting (1) from (2) and considering that l1i = l1c = l1, we obtain
l2c – l2i = l1 \frac{{\left( {{{\alpha }_{c}}-{{\alpha }_{i}}} \right)\left( {{{t}_{2}}-{{t}_{1}}} \right)}}{{\left( {1+{{\alpha }_{c}}{{t}_{1}}} \right)\left( {1+{{\alpha }_{i}}{{t}_{1}}} \right)}} =19.9 mm
For low values of temperature t, when át < 1, it is not necessary to reduce l1 and l2 to lo1 and lo2 at t = 0 oC. To a sufficiently high degree of accuracy, we an assume that Äl = láÄt. Under this assumption, the problem can be solved in a simpler way:
li = l1iái(t2 – t1), lc = l1các(t2 – t1)
Consequently, since l1i = l1c = l1, we have
l = lc – li = l1(t2 – t1)(ác – ái) = 20 mm
It can been seen that the deviation from a more exact value of 19.9 mm amounts to 0.1 mm, i.e. the relative error Ä = 0.1/19.9 = 0.5%.
Illustration
A solid body floats in a liquid at a temperature t = 0o C and is completely submerged in it at 50o C. What fractiond of volume of the body is submerged in the liquid at 0o C if
gs = 0.3 x 10-5 K-2 and of the liquid, g1 = 8.0 x 10-5 K-1?
Solution
In both the cases the weight of the body will be balanced by the force of buoyancy on it.
At to= 0 oC, the buoyancy is
Fb= dVoñog (1)
whereVois the volume of the body and ño is the density of the liquid at to= 0oC. At t = 50 oC, the volume of the body becomes V = Vo(1 + gst) and the density of the liquid is ñ1 = ño/(1 + g1t). The buoyancy in this case is
Fb= Voñog(1 + gst)/(1 + g1t) (2)
Equating the right-hand sides of equation (1) and (2), we get
d = (1 + gst)/(1 + g1t) = 96%
Illustration
A metallic ball has spherical cavity at its centre. If the ball is heated, the ratio of volume of ball to that of volume of cavity will
(a) increase
(b) decrease
(c) remain same
(d) depends on the volume of cavity
Solution
\frac{{{{V}_{b}}(1+\gamma \Delta \theta )}}{{{{V}_{c}}(1+\gamma \Delta \theta )}}=\frac{{{{V}_{b}}}}{{{{V}_{c}}}}=const
(c)
Practice Questions (Basic Level)
1.
Two rods of lengths {{l}_{1}} and {{l}_{2}} are made of materials whose coefficients of linear expansion are {{\alpha }_{1}} and {{\alpha }_{2}} respectively. If the difference between the two lengths is independent of temperature, then
(a) \frac{{{{l}_{1}}}}{{{{l}_{2}}}}=\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}}}}
(b) \frac{{{{l}_{1}}}}{{{{l}_{2}}}}=\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{2}}}}
(c) l_{1}^{2}{{\alpha }_{2}}=l_{2}^{2}{{\alpha }_{1}}
(d) \alpha _{2}^{2}{{l}_{1}}=\alpha _{1}^{2}{{l}_{2}}
Ans (a)
2.
A bimetal made of copper and iron strips welded together is straight at room temperature. It is held vertically in the hand, such that iron strip is towards the left hand and copper strip is towards the right hand side. This bimetal is then heated by flame. The bimetal strip will
(a) remain straight
(b) bend towards right
(c) bend towards left
(d) no change
Ans (b)
Practice Questions (JEE Main Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
