Video Lecture
Theory For Making Notes
Lorentz force
The force experienced by a charged particle moving in space where both electric and magnetic fields exist is called Lorentz force.
Force due to electric field: When a charge particle carrying charge +q is subjected to an electric field of strength \vec{E}, it experiences a force given by {{\vec{F}}_{e}}=q\vec{E}. Whose direction is the same at that of \vec{E}.
Force due to magnetic field: IF the charged particle is moving in a magnetic field , with a velocity it experiences a force given by
{{\vec{F}}_{m}}=q(\vec{v}\times \vec{B})
The direction of this force is in the direction of (\vec{v}\times \vec{B}) i.e. perpendicular to the plane containing \vec{v} and \vec{B} and is directed as given by right hand screw rule.
Due to both the electric and magnetic fields, the total force experienced by the charged particle will be given by
\vec{F}={{\vec{F}}_{e}}+{{\vec{F}}_{m}}=q\vec{E}+q(\vec{v}\times \vec{B})
=q(\vec{E}+\vec{v}\times \vec{B})
This is called Lorentz force.
Special case:
(a) When \vec{v},\,\,\vec{E} and \vec{B}, all the three are collinear. In this situation the charged particle is moving parallel or antiparallel to the fields, the magnetic force on the charged particles is zero. The electric force on the charged particle will produce acceleration \vec{a}=\frac{{q\vec{E}}}{m}, Along the direction of electric field. As a result of which there will be change in the speed of charged particle along the direction of the field. In this situation there will be no change in the direction of motion of the charged particle but, the speed, velocity, momentum and kinetic energy all will change.
(b) When \vec{v},\vec{E} and \vec{B} are mutually perpendicular to each other. In this situation if \vec{E} and \vec{B} are such that \vec{F}={{\vec{F}}_{e}}+{{\vec{F}}_{m}}=0, It means the particle will pass through the fields without any change in its velocity. Here, \displaystyle {{\vec{F}}_{e}}=-{{\vec{F}}_{m}} so in magnitude the two forces are equal but opposite in direction.
Hence qE=qv\,B or v = E / B
Note that while passing through a region having magnetic and electric field both, with a condition that the velocity of the charge particle , magnetic field and electric field all are mutually perpendicular,then only those charge particles can move straight (or undeviated or unaccelerated) whose velocity is given by the above equation because the net force on it is zero
This concept has been used in velocity-selector to get a charged beam having a definite velocity.
(c) If the charge particle is moving through a region having only magnetic field with its velocity parallel to field, then the force acting on the particle is zero and it goes straight.
Motion of a charged particle in a Uniform Magnetic Field
Case-1
Consider the motion of a positively charged particle moving with an initial velocity \vec{v}perpendicular to a uniform magnetic field \vec{B} as shown in figure given below.
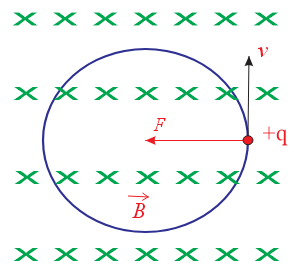
Since \vec{v} and \vec{B} are perpendicular, the particle experiences a force F = qvB of constant magnitude directed perpendicular to \vec{v}. Under the action of such a force the particle moves in a circular path with constant speed. The magnetic force provides the centripetal force. Applying Newton’s second law
qvB = \frac{{m{{v}^{2}}}}{r}
where r is the radius of the circular path.
r = \frac{{mv}}{{qB}}
The radius of the orbit is directly proportional to the linear momentum of the particle and inversely proportional to the magnetic field strength.
The time period is given by
T = \frac{{2\pi r}}{v}=\frac{{2\pi m}}{{qB}}
Note that time period is independent of velocity. All particles with same charge to mass ratio (q/m), have the same period.
Case-2
Suppose a particle of mass m and charge q, entering a uniform magnetic field induction \vec{B} at O, with velocity \vec{v}, making an angle \theta with the direction of magnetic field acting in the plane of paper as shown in figure.
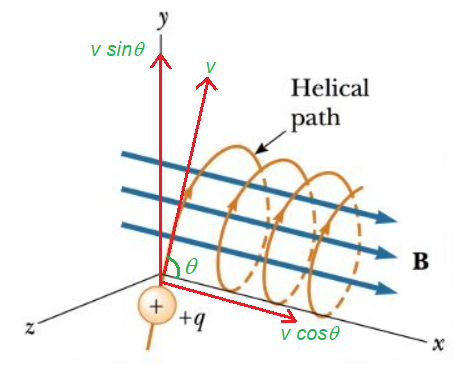
Resolving \vec{v} into two rectangular components we have:
v\cos \theta (={{v}_{1}}) acts in the direction of the magnetic field and v\sin \theta (={{v}_{2}}) acts perpendicular to the direction of magnetic field.
For component velocity {{\vec{v}}_{2}}, the force acting on the charged particle due to magnetic field is
\vec{F}=q({{\vec{v}}_{2}}\times \vec{B})
or F=q|{{\vec{v}}_{2}}\times \vec{B}|=q{{v}_{{2\,\,}}}B\,\sin 90{}^\circ
=q(v\sin \theta )\,B …(i)
The direction of this force \vec{F} is perpendicular to the plane containing \vec{B}and {{\vec{v}}_{2}} and hence acts perpendicular to the plane of the paper. As this force is to remain always perpendicular to {{\vec{v}}_{2}}, it can not change the magnitude of velocity {{\vec{v}}_{2}}. It changes only the direction of motion. Hence the charged particle is made to move on a circular path in the magnetic field, as shown in figure with dotted circle. The force F on the charged particle due to magnetic field provides the required centripetal force (=mv_{2}^{2}/r) necessary for motion along the circular path of radius.
\therefore B\,q\,{{v}_{2}}=mv_{2}^{2}/r
or {{v}_{2}}=B\,qr/m
or v\sin \theta =Bqr/m …(ii)
The angular velocity of rotation of the particle in magnetic field will be
\omega =\frac{{v\sin \theta }}{r}=\frac{{B\,qr}}{{mr}}=\frac{{B\,q}}{m}
The frequency of rotation of the particle in magnetic field will be
v=\frac{\omega }{{2\pi }}=\frac{{B\,q}}{{2\pi \,m}} …(iii)
The time period of revolution of the particle in the magnetic field will be
T=\frac{1}{v}=\frac{{2\pi \,m}}{{B\,q}} …(iv)
From (iii) and (iv) we note that and T do not depend upon velocity \vec{v} of the particle. It means, all the charged particles having the same specific charge (charge/mass) but moving with different velocities at a point, will complete their circular paths in the same time.
For component velocity {{v}_{1}}=(v\,\cos \,\theta ), there will be no force on the charged particle in the magnetic field, because, the angle between {{\vec{v}}_{1}} and \vec{B} is zero. Thus the charged particle covers the linear distance in direction of the magnetic field with a constant speed v\cos \theta .
Therefore, under the combined effect of the two component velocities, the charged particle in magnetic field will move on a circular pathe as well as it cover linear distance along the magnetic field so the resultant path of the charged particle will be helical in shape and is called Halix whose axis is parallel to the direction of magnetic field.
The linear distance covered by the charge particle in the magnetic field in time equal to one revolution of its circular path is known as pitch of helix.
Hence Pitch `d’ can be calculated as follows
d={{v}_{1}}T=v\,\,\cos \theta \,\,\frac{{2\pi m}}{{Bq}}.
Note:
(a) If a charged particle having charge is at rest on a magnetic field \vec{B}, it experiences no force, as v=0 and F=q\,v\,B\sin \theta
(b) If charged particle is moving parallel to the direction of \vec{B}, it also does not experience any force because angle \theta between \vec{v} and \vec{B} is \displaystyle {{0}^{o}}or{{180}^{o}}
because \sin 0{}^\circ =\sin 180{}^\circ =0. Therefore, the charged particle in this situation will continue moving along the same path with the same velocity.
(c) if charged particle is moving perpendicular to the direction of \vec{B}, it experiences a maximum force which acts perpendicular to the direction of \vec{B} as well as . Hence this force will provide the required centripetal force and the charged particle will describe a circular path in the magnetic field to radius , given by \frac{{m{{v}^{2}}}}{r}=Bq\,v
When a charged a particle is projected perpendicular to the magnetic field, (i) its path is circular in a plane perpendicular to the plane of magnetic field and direction of motion of the charged particle. (ii) the speed and kinetic energy of the particle remain constant. (iii) The velocity of the charged particle changes only in direction. The force acting on the charged particle is independent of the radius of circular path but depends upon the speed of the charged particle i.e., F\propto \,r{}^\circ (but F\propto \,v). (v) The time period of revolution of a charged particle in the magnetic field is independent of velocity of particle and radius of the circular path i.e., T\,\propto \,\,{{r}^{o}}\,{{v}^{o}}.
Work done by a Magnetic Force is zero.
Since \vec{F} is always perpendicular to \vec{v} there is no component of acceleration in the direction of velocity vector, therefore, magnitude of the velocity does not change, thus kinetic energy of the charge does not change, hence no work is done by the magnetic force.
Mathematically, it can be proved like this W=\int{{\vec{F}.\overrightarrow{{ds}}}} \displaystyle =\int{{q(\vec{v}\times \vec{B}).\overrightarrow{{ds}}}} Since \displaystyle \overrightarrow{{ds}}=\vec{v}dt Therefore \displaystyle W=q\int{{(\vec{v}\times \vec{B})\cdot }}\text{ }\vec{v}dt\text{ = 0} Illustration : An electron with a kinetic energy of 103 eV moves perpendicular to the direction of uniform field B = 10–4 T. (a) What is the period of its orbit ? (b) What is the radius of its orbit ? Solution(a) Using equation of Time period T = \frac{{2\pi m}}{{eB}}=\frac{{2\pi (9.1\times {{{10}}^{{-31}}}\ kg)}}{{(1.6\times {{{10}}^{{-19}}}C)\ ({{{10}}^{{-4}}}T)}} or T = 3.6 ´ 10-7s (b) Using equation of the radius of the orbit r = \frac{{mv}}{{eB}}=\frac{p}{{eB}} , where p is the momentum The momentum of the electron can be obtained from kinetic energy as mv = \sqrt{{2Km}}=\sqrt{{2(1.6\times {{{10}}^{{-16}}}J)\ (9.1\times {{{10}}^{{-31}}}kg)}}= 1.7 ´ 10–23 kg m/s Thus, radius of the orbit is given by r = \frac{{(1.7\times {{{10}}^{{-23}}}\ kg\ m/s)}}{{(1.6\ \times \ {{{10}}^{{-19}}}C)\ ({{{10}}^{{-4}}}T)}} = 1.07 m Illustration : A particle of mass m and charge q is projected into a region having a perpendicular uniform magnetic field B. Find the angle \theta of deviation of the particle as it comes out of the magnetic field if width d of the region is equal to (a) \frac{{mv}}{{2qB}} (b) \frac{{mv}}{{qB}} (c) \frac{{2mv}}{{qB}} |
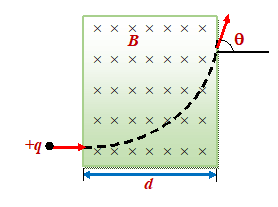
Solution
(a) The radius of the circular orbit is given by
r = \frac{{mv}}{{qB}}
The angle of deviation is given by sinq
= \frac{d}{r}= \frac{1}{2}\ \ \ \ \left( {\because d=\frac{{mv}}{{2qB}}=\frac{r}{2}} \right)
or
\displaystyle \theta ={{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)=\frac{\pi }{6}
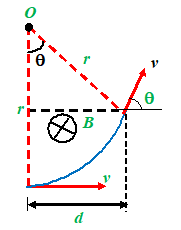
(b) When d = \frac{{mv}}{{qB}} = r, the charged particle deviates through an angle of \frac{\pi }{2} as shown
in the figure , hence \theta =\frac{\pi }{2}
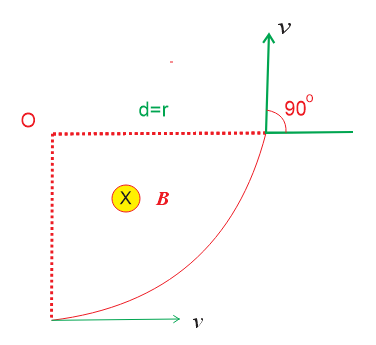
(c)When d = 2 \frac{{mv}}{{qB}}= 2r, the charged particle completes one semi-circle and deviates through \pi , as shown in the figure, hence \theta =\pi
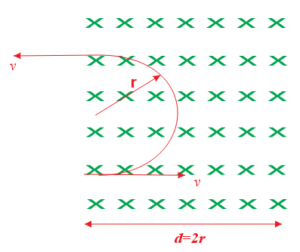
Illustration
An electron moving at 4 x 106 m/s enters a uniform field B = 0.04 T at \displaystyle {{30}^{o}} to the magnetic field lines. What is the pitch of the helical path.
Solution
\displaystyle {{v}_{\parallel }}=v.\cos \theta where v = 4 x 106 m/s ; \theta ={{30}^{o}}
\displaystyle \therefore {{v}_{{||}}}=\text{ }(4\times {{10}^{6}})\text{ }cos30{}^\circ \text{ }=\text{ }3.46\times {{10}^{6}}m/s Using equation
p = \frac{{2\pi m{{v}_{{||}}}}}{{qB}}
or p = 2 \pi \frac{{(9.1\ \times {{{10}}^{{-31}}})\ (3.46\times {{{10}}^{6}})}}{{(1.6\times {{{10}}^{{-19}}})\ (0.04)}} = 3.1 mm
Illustration:
Uniform electric \vec{E} and magnetic \vec{B} field are directed along the y – axis as shown in the figure . A particle with specific change (q/m) leaves the origin O along the x-axis with velocity vo.
(a) Find the coordinate yn of the particle when it crosses the y-axis for the nth time.
(b) Find the angle between the particle vector and the y-axis at that moment.
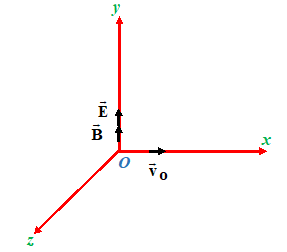
Solution
(a) Since magnetic field does not accelerate a particle in its own direction, therefore, the distance moved along the y-axis is only due to electric field.
ay = \frac{{qE}}{m}
The period T = \frac{{2\pi m}}{{qB}}
The time taken for n revolution is t = nT = \frac{{2\pi nm}}{{qB}}
The distance travelled along the y-axis is
yn = \frac{1}{2}ayt2 = \frac{1}{2} \left( {\frac{{qE}}{m}} \right)\ {{\left( {\frac{{2\pi nm}}{{qB}}} \right)}^{2}}
(b) The velocity parallel to the y-axis after time t
v|| = ayt = \frac{{qEt}}{m}=\frac{{2\pi nE}}{B}
Velocity \displaystyle {{v}_{\bot }} to the y-axis is
\displaystyle {{v}_{\bot }}={{v}_{o}}
Now, tan q = \frac{{{{v}_{\bot }}}}{{{{v}_{{||}}}}} = \frac{{{{v}_{o}}B}}{{2\pi nE}}
or q = tan–1 \left( {\frac{{{{v}_{o}}B}}{{2\pi nE}}} \right)
Illustration
A particle of charge +q and mass m moving under the influence of a uniform electric field E \overset{\to }{\mathop{i}}\, and a uniform magnetic field B \overset{\to }{\mathop{k}}\, follows a trajectory from P to Q as shown in Figure.
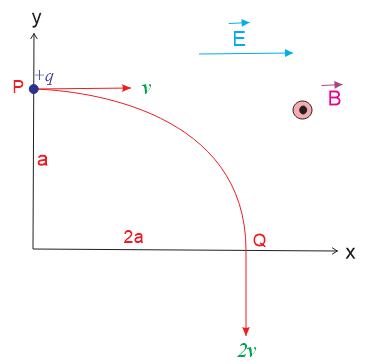
The velocity at P and Q are v \overset{\to }{\mathop{i}}\, and – 2v \overset{\to }{\mathop{j}}\,. Which of the following statement/s is/are correct?
(1) E\ =\ \frac{3}{4}\ \left( {\frac{{m{{v}^{2}}}}{{qa}}} \right)
(2) Rate of work done by the electric field at P is \frac{3}{4}\ \left( {\frac{{m{{v}^{3}}}}{a}} \right)
(3) Rate of work done by the electric field at P is zero.
(4) Rate of work done by both of the fields at Q is different.
Solution: Work done by electric filed = Gain in kinetic energy
Þ (qE) ´ (2a) = \frac{1}{2}m[{{(2v)}^{2}}-{{v}^{2}}]
Þ qE ´ 2a = \frac{1}{2}m\times 3{{v}^{2}}\Rightarrow E=\frac{3}{4}\left( {\frac{{m{{v}^{2}}}}{{qa}}} \right)\
hence option (1) is correct
Rate of work done by electric filed at P = \overset{\to }{\mathop{F}}\,\cdot \overset{\to }{\mathop{v}}\,= (qE) . v
= qv\times \frac{3}{4}\left( {\frac{{m{{v}^{2}}}}{{qa}}} \right) = \frac{\mathbf{3}}{\mathbf{4}}\left( {\frac{{\mathbf{m}{{\mathbf{v}}^{\mathbf{2}}}}}{\mathbf{a}}} \right)\
hence option (2) is correct
At P the electric field and velocity of charge are in the same direction so rate of work done by the electric field can not be zero.
hence option (3) is wrong
At Q the work done by both the fields is zero.
hence option (4) is wrong
Illustration
Starting with Lorentz force, show that motion of a charged particle in a magnetic field is circular.
Solution: Consider a charge q in a uniform magnetic field B. Let us take the direction of the field as z-axis. This does not mean loss in generality.
Lorentz force F =q(\vec{v}\times \vec{B})
hence F =q\left| \begin{array}{l}\overset{\wedge }{\mathop{i}}\,\text{ }\overset{\wedge }{\mathop{j}}\,\text{ }\overset{\wedge }{\mathop{k}}\,\\{{v}_{x}}\text{ }{{v}_{y}}\text{ }{{v}_{z}}\\0\text{ 0 B}\end{array} \right|
therefore
ma =q\left| \begin{array}{l}\overset{\wedge }{\mathop{i}}\,\text{ }\overset{\wedge }{\mathop{j}}\,\text{ }\overset{\wedge }{\mathop{k}}\,\\{{v}_{x}}\text{ }{{v}_{y}}\text{ }{{v}_{z}}\\0\text{ 0 B}\end{array} \right|
\displaystyle m\left( {\frac{{dV}}{{dt}}} \right)\, =q\left| \begin{array}{l}\overset{\wedge }{\mathop{i}}\,\text{ }\overset{\wedge }{\mathop{j}}\,\text{ }\overset{\wedge }{\mathop{k}}\,\\{{v}_{x}}\text{ }{{v}_{y}}\text{ }{{v}_{z}}\\0\text{ 0 B}\end{array} \right|
\displaystyle \Rightarrow \text{ }m\,\frac{d}{{dt}}({{v}_{x}}\hat{i}+{{v}_{y}}\hat{j}+{{v}_{z}}\hat{k}) =q\left| \begin{array}{l}\overset{\wedge }{\mathop{i}}\,\text{ }\overset{\wedge }{\mathop{j}}\,\text{ }\overset{\wedge }{\mathop{k}}\,\\{{v}_{x}}\text{ }{{v}_{y}}\text{ }{{v}_{z}}\\0\text{ 0 B}\end{array} \right|
hence \displaystyle m\frac{{d{{v}_{x}}}}{{dt}}\overset{\wedge }{\mathop{i}}\,+m\frac{{d{{v}_{y}}}}{{dt}}\overset{\wedge }{\mathop{j}}\,+m\frac{{d{{v}_{z}}}}{{dt}}\overset{\wedge }{\mathop{k}}\,=q{{v}_{y}}B\overset{\wedge }{\mathop{i}}\,-q{{v}_{x}}B\overset{\wedge }{\mathop{{j+}}}\,0\overset{\wedge }{\mathop{k}}\,
Equating coefficients of \hat{i}, \hat{j} and \hat{k} we have
q{{v}_{y}}B=m\frac{{d{{v}_{x}}}}{{dt}},\,\,-q{{v}_{x}}B=m\frac{{d{{v}_{y}}}}{{dt}}\,\,and\,\,m\frac{{d{{v}_{z}}}}{{dt}}=0
\frac{{d{{v}_{x}}}}{{dt}}=\frac{{qB}}{m}{{v}_{y}},\,\,\frac{{d{{v}_{y}}}}{{dt}}=-\frac{{qB}}{m}{{v}_{x}}\,\,and\,\,\frac{{d{{v}_{z}}}}{{dt}}=0 ……… (i)
The last equation shows that {{v}_{z}} is a constant.
Since the Lorentz force is perpendicular to the velocity no work is done by it and hence the kinetic energy of the charged particle remains constant in a magnetic field.
\frac{1}{2}m({{v}_{x}}^{2}+{{v}_{y}}^{2}+{{v}_{z}}^{2}) = a constant
{{v}_{x}}^{2}+{{v}_{y}}^{2} = a constant = {{v}_{0}}^{2} ( \because {{v}_{z}} is a constant) ………(ii)
This is equation of a circle of radius {{v}_{0}}. This means that velocity is rotating vector of fixed magnitude rotating in the x–y plane, that is, in the plane perpendicular to the magnetic field. Hence we can write {{v}_{x}}={{v}_{0}}\cos \theta and {{v}_{y}}={{v}_{0}}\sin \theta , where \theta is the angle made by with x–axis.
Now substituting in any one of the first two equation in (i)
\frac{{d\theta }}{{dt}}=-\frac{{qB}}{m}=-\omega (say), where \omega =\frac{{qB}}{m}
\theta =-\omega t+{{\theta }_{0}}, where {{\theta }_{0}} is the constant of integration
{{v}_{x}}=\frac{{dx}}{{dt}}={{v}_{0}}\cos (-\omega t+{{\theta }_{0}}) and {{v}_{y}}=\frac{{dy}}{{dt}}={{v}_{0}}\sin (\omega t+{{\theta }_{0}})
\frac{{dx}}{{dt}}={{v}_{0}}\cos (\omega t-{{\theta }_{0}}) and \frac{{dy}}{{dt}}=-{{v}_{0}}\sin (\omega t-{{\theta }_{0}})
Integrating we get
x=\frac{{{{\upsilon }_{0}}}}{\omega }\sin (\omega t-{{\theta }_{0}})+{{x}_{0}} (where {{x}_{0}} is the constant of integration)
and y=-\frac{{{{\upsilon }_{0}}}}{\omega }\cos (\omega t-{{\theta }_{0}})+{{y}_{0}} (where {{y}_{0}} is the constant of integration)
Eliminating t between these two equations of x and y coordinates we have
{{(x-{{x}_{0}})}^{2}}+{{(y-{{y}_{0}})}^{2}}={{\left( {\frac{{{{\upsilon }_{0}}}}{\omega }} \right)}^{2}}
This is equation of a circle with center at the point ({{x}_{0}},{{y}_{0}}) and with radius \left( {\frac{{{{\upsilon }_{0}}}}{\omega }} \right).
Illustration
A beam of charged particles of K.E. = 1 keV and q = 1.6 ´ 10–19 C and two
masses 8 ´ 10–22 kg and 16 ´ 10–27 kg come out of an accelerator tube.
And strike a plate at distance of 1 cm from the end of the tube, from where
the particles emerge perpendicularly. The value of the smallest magnetic
field which can prevent the beam from striking the plate is
(1) 1.414 T (2) 2.828 T (3) 4.242 T (4) 5.656 T
Solution:
\vec{B} should be out of the paper. Let F be the magnetic force acting on the particles, where F = (mv2/r) = qvB since v is perpendicular to B. This force does not change the velocity of the particles but it bends them into a circular arc of radius r, where r = \left( {\frac{{mv}}{{qB}}} \right). The beam will not strike the plate,if the radius of path of the beam is at the most 1cm. So minimum magnetic field required is given by the equation of the radius Hence {{r}_{{\max }}}=\ \left( {\frac{{mv}}{{q{{B}_{{\min }}}}}} \right).
Bmin = \frac{{mv}}{{q\ \times \ {{{10}}^{{-2}}}}}\ =\ \frac{{mv}}{{(1.6\ \times \ {{{10}}^{{-19}}}\ \times \ {{{10}}^{{-2}}})}}
Now \frac{1}{2}\ m{{v}^{2}} = K.E. = 1.0 keV = 103 eV = 103 ´ 1.6 ´10–19 J
or v = (2 ´ 103 ´ 1.6 ´ 10-19 J/m)1/2 .
Bmin = \frac{{m\ \times \ {{{\left( {\frac{{2\ \times \ {{{10}}^{3}}\ \times \ 1.6\ \times \ {{{10}}^{{-19}}}}}{m}} \right)}}^{{1/2}}}}}{{1.6\ \times \ {{{10}}^{{-19}}}\times \ {{{10}}^{{-2}}}}}
= \sqrt{m}\ \sqrt{{\frac{{2\ \times \ {{{10}}^{3}}\times \ 1.6\ \times \ {{{10}}^{{-19}}}}}{{{{{(1.6\ \times \ {{{10}}^{{-21}}})}}^{2}}}}}}\ =\ \sqrt{m}\ {{\left[ {\frac{{3.2\ \times \ {{{10}}^{{-16}}}}}{{2.56\ \times \ {{{10}}^{{-42}}}}}} \right]}^{{1/2}}}
= \sqrt{m}\ \times \ {{(1.25\ \times \ {{10}^{{26}}})}^{{1/2}}}=\ \sqrt{m}\ \times \ 1.1\ \times \ {{10}^{{13}}}
Hence, Bmin is more if m is more. The higher masses can be prevented from striking the plate, if
Bmin =\ \sqrt{{16\ \times \ {{{10}}^{{-27}}}}}\ \sqrt{{1.25}}\ \times \ {{10}^{{13}}}
= (\sqrt{{1.6\ \times \ 1.25)}}\ =\ (\sqrt{2}) T = 1.414 T
Hence option (1) is correct
Practice Questions (Basic Level)
Q.1
A charged particle moves through a magnetic field. The effect of the field is to change the particle’s
(a) speed (b) direction of motion (c) energy (d) acceleration
Ans : (b)
Q.2
A charged particle is moved along a magnetic field line. The force on the particle is
(a) along its velocity
(b) opposite to its velocity
(c) perpendicular to its velocity
(d) zero
Ans : (d)
Q.3
Electrons moving with a constant velocity enter a uniform magnetic field B in a direction perpendicular to B. The electron path in the field is
(a) a helix
(b) a straight line parallel to B
(c) a straight line perpendicular to B
(d) a circle
Ans : (d)
Q.4
A beam of ions with velocity 2 ´ 105 m/s enter normally into a uniform magnetic field of
4 ´ 10-2 T. If the specific charge of the ions is 5 ´ 107 C/kg, the radius of the circular path described will be
(a) 0.10 m (b) 0.16 m (c) 0.20 m (d) 0.25 m
Ans : (a)
Q.5
If electron velocity is \left( {2\hat{i}+3\hat{j}} \right) and it is subjected to a magnetic field , then:
(a) speed will change
(b) path will change
(c) both (a) and (b)
(d) none of the above
Ans : (b)
Q.6
Two particles x and y having equal charges after being accelerated through the same p.d. enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of x and y is
(a) (R1/R2)1/2 (b) (R2/R1) (c) (R1/R2)2 (d) (R1/R2)
Ans : (c)
Q.7
An electron is moving in a circle of radius r in a uniform magnetic field B. Suddenly the field is reduced to B/2. The radius of the circle now becomes.
(a) r/2 (b) r/4 (c) 2r (d) 4r
Ans : (c)
Q.8
A positively charged particle moving with velocity enters a region of space having a constant magnetic induction . The particle will experience the largest force when the angle between vectors and is :
(a) 0° (b) 45° (c) 90° (d) 180°
Ans : (c)
Q.9
An electron accelerated through a potential difference V passes through a uniform transverse magnetic field and experiences a force F. If the accelerating potential is increased to 2V, the electrons in the same magnetic field will experience a force
(a) \sqrt{2}F
(b) 2F
(c) 2\sqrt{2}F
(d) 4F
Ans. (a)
Q.10
A charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
(a) \displaystyle \sqrt{{\frac{{Vm}}{{q{{B}^{2}}}}}}
(b) \displaystyle \frac{{2Vm}}{{q{{B}^{2}}}}
(c) \displaystyle \sqrt{{\frac{{2Vm}}{q}}}\left( {\frac{1}{B}} \right)
(d) \displaystyle \sqrt{{\frac{{Vm}}{q}}}\left( {\frac{1}{B}} \right)
Ans. (c)
Q.11
The acceleration of an electron at a certain moment in a magnetic field B=2\hat{i}+3\hat{j}+4\hat{k} is a=x\,\,\hat{i}+\hat{j}-\hat{k}. The value of x is
(a) 0.5 (b) 1 (c) 2.5 (d) 1.5
Ans. (a)
Q.12
Two charged particles P and Q enter a uniform magnetic field normally with the same speed. Their paths in the field are as shown in the figure. It can be concluded that
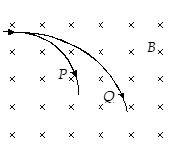
(a) the charge of P is greater than that of Q
(b) the specific charge of P is greater than that of Q
(c) both P and Q are positively charged
(d) both P and Q have same mass
Ans. (b)
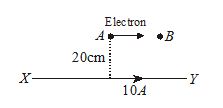
13.
A long straight wire carries a current of 20 A. An electron at a distance of 10 cm from it is moving with a velocity of {{10}^{6}}\,\,m{{s}^{{-1}}}. What is the force on the electron when
(i)
it is moving parallel to the wire
(a) 6.4\times {{10}^{{-18}}}\,\,N
(b) 6.4\times {{10}^{{18}}}\,\,N
(c) 6.4\times {{5}^{{18}}}\,\,N
(d) 6.4\times {{5}^{{-18}}}\,\,N
Ans (b)
(ii)
it is moving towards the wire and
(a) 6.4\times {{10}^{{-18}}}\,\,N
(b) 6.4\times {{10}^{{18}}}\,\,N
(c) 6.4\times {{5}^{{18}}}\,\,N
(d) 6.4\times {{5}^{{-18}}}\,\,N
Ans (a)
(iii)
it is moving perpendicular to the above two directions?
(a)zero
(b)5
(c)3
(d)2
Ans (a)
14.
A 10\,eVelectron is circulating in a plane at right angles to a uniform field of a magnetic induction of {{10}^{{-4}}}\,\,\mathbf{Tesla}. What is the radius of its orbit?
(a)0.1 m
(b)0.11 m
(c)0.21 m
(d)0.30 m
Ans (b)
15.
A rectangular lop of side a = 25 cm and b = 10 cm carrying a current I=15\,\,A is placed with its longer side parallel to a long conductor d = 2.0 cm apart carrying a current I’=25\,\,A. What is the net force on the loop?
(a) 7.8\times {{10}^{{-5}}}\,\,N
(b) 7.5\times {{10}^{{-5}}}\,\,N
(c) 7.0\times {{10}^{{-5}}}\,\,N
(d) 8.5\times {{10}^{{-5}}}\,\,N
Ans (a)
16.
A flat silver strip of width 2.0 cm and thickness 1.0 mm carries a current to 10 A. A magnetic field of 0.2 T is applied perpendicular to the flat face of the strip. The emf developed across the width of the strip is measured to be 2\mu V. Find the density of free electrons in the metal.
(a) 6.5\times {{10}^{{28}}}
(b) 6.25\times {{10}^{{28}}}
(c) 6.00\times {{10}^{{28}}}
(d) 6.25\times {{10}^{{-28}}}
Ans (b)
17.
An infinite long straight conductor XY is carrying a current of 10A. An electron is moving with a speed of parallel to the conductor in air from point A to B, as shown in figure. The perpendicular distance between the electron and the conductor XY is 20 cm. Calculate the magnitude of the force experienced by the electron. Write the direction of this force
(a) 1.6\times {{5}^{{19}}}\,N
(b) 1.6\times {{5}^{{-19}}}\,N
(c) 1.6\times {{10}^{{-19}}}\,N
(d) 1.6\times {{10}^{{19}}}\,N
Ans (c)
18.
A proton and an \alpha -particle enter a uniform magnetic field at right angles to it with same velocity. Find the ratio of time period of revolution \alpha -particle and the proton.
(a)2 : 5
(b)2 : 3
(c)2 : 1
(d)1 : 3
Ans (c)
19.
A beam of charged particles having kinetic energy and containing masses 8\times {{10}^{{-27}}}\,kgand 1.6\times {{10}^{{-26}}}\,kg, emerges from the end of an accelerated tube. There is a plate at a distance \displaystyle {{10}^{{-2}}}m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plane.
(a) \frac{{\sqrt{5}}}{q}\times 1.6\times {{10}^{{-19}}}T
(b) \frac{{\sqrt{2}}}{q}\times 2\times {{10}^{{-20}}}T
(c) \frac{{\sqrt{2}}}{q}\times 1.6\times {{10}^{{-19}}}T
(d) \frac{{\sqrt{2}}}{q}\times 1.6\times {{10}^{{19}}}T
Ans (c)
20.
An electron beam passes through a magnetic field of 2\times {{10}^{{-3}}}\mathbf{weber/}{{\mathbf{m}}^{\mathbf{2}}} and an electric field of 1.0\times {{10}^{4}}\,\,V{{m}^{{-1}}}both acting simultaneously. The path of electrons remaining undeviated, calculate the speed of the electrons. If the electric field is removed what will be the radius of the electron path?
(a) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(b) 3\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(c) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
(d) 5\times {{10}^{6}}\,m{{s}^{{-1}}};\,\,\,1.43\,\,cm
Ans (a)
Practice Questions (JEE Main Level)
Q.1
The path of a charged particle in a region with uniform electrostatic and a magnetic fields parallel to each other, with some initial velocity perpendicular to the common direction of the fields is
(a) A circle (b) An ellipse (c) A cycloid (d) Parabola
Ans: (a)
Q.2
The path of a charged particle in a region of crossed electric and magnetic fields is
(a) A circle (b) An ellipse (c) A cycloid (d) A parabola
Ans: (c)
Q.3
The path of a charged particle into a region of uniform magnetic field at an arbitrary and arbitrary velocity is
(a) A circle (b) An ellipse (c) A parabola (d) A helix
Ans: (d)
Q.4
{{H}^{+}}, H{{e}^{+}} and {{O}^{{++}}} all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity. The masses of {{H}^{+}}, H{{e}^{+}} and {{O}^{{++}}} are 1 amu, 4 amu and 16 amu respectively. Then
(a) {{H}^{+}}will be deflected most
(b) {{O}^{{++}}} will be deflected most
(c) H{{e}^{+}} and {{O}^{{++}}} will be deflected equally
(d) All will be deflected equally
Ans: (a)
Q.5
Two particles X and Y having equal charges, after being accelerated through the same potential difference, enters a region of uniform magnetic field and describe circular paths of radii \displaystyle {{R}_{1}} and {{R}_{2}} respectively. The ratio of the masses X to Y is
(a) {{\left( {\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right)}^{{\frac{1}{2}}}}
(b) \frac{{{{R}_{2}}}}{{{{R}_{1}}}}
(c) {{\left( {\frac{{{{R}_{1}}}}{{{{R}_{2}}}}} \right)}^{2}}
(d) \frac{{{{R}_{1}}}}{{{{R}_{2}}}}
Ans: (c)
Q.6
A charged particle moves through a magnetic field in a direction perpendicular to it, then
(a) The speed of the particle remains unchanged
(b) The direction of particle remains unchanged
(c) Acceleration remains unchanged
(d) Velocity remains unchanged
Ans. (a)
Q.7
A charged particle of mass m, carrying charge q enters a magnetic field B at right angle to it. The path traced out it is a circle. The time period of the particle will be
(a) \frac{{2\pi }}{{qmB}}
(b) \frac{{2\pi B}}{{mq}}
(c) \frac{{2\pi q}}{{mB}}
(d) \frac{{2\pi m}}{{Bq}}
Ans. (d)
Q.8
A particle of mass m=1.6\times {{10}^{{-27}}}kg and charge q=1.6\times {{10}^{{-19}}}C moves at a speed of 1.0\times {{10}^{7}}m{{s}^{{-1}}}. It enters a region of uniform magnetic field at a point E, as shown in figure. The field has a strength of 1.0 T. The magnetic field is directed into the plane of the paper. The particle leaves the region of the field at the point F. Find the distance EF.
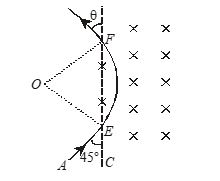
(a) 28 cm (b) 57 cm (c) 14 cm (d) 7 cm
Ans. (b)
Q.9
An unchanged particle enters a region of non–uniform field and eventually comes out of it. As it emerges, its
(a) Speed is greater as compared to the speed at entry point
(b) Velocity remains unchanged
(c) Velocity may change but speed remains unchanged
(d) Speed cannot be estimated as data is insufficient
Ans. (c)
Q.10
An electron is accelerated to a high speed down on the axis of a cathode ray tube by the application of a potential difference of V volts between the cathode and the anode. The particle then passes through a uniform transverse magnetic field in which it experiences a force F. If the potential difference between the anode and the cathode is increased to 2 V, the electron will now experience a force
(a) F/\sqrt{2}
(b) F/2
(c) \sqrt{2}F
(d) 2F
Ans. (c)
Q.11
The direction of the force experienced by a charged particle moving with a velocity v in a uniform magnetic field B is
(a) Parallel to v and perpendicular to B
(b) Parallel to B and perpendicular to v
(c) Parallel to both v and B
(d) Perpendicular to both v and B
Ans. (d)
Q.12
If protons are shot perpendicular to a magnetic field
(a) Magnetic field will have no influence on the motion of protons
(b) Protons will continue to move in the same direction but will gain momentum
(c) Protons will continue to move in the opposite directions but will gain momentum
(d) They will bend in an arc of a circle
Ans. (d)
Q.13
It a proton is projected in a direction perpendicular to a uniform magnetic field with velocity v and an electron is projected along the lines of force, what will happen to proton and electron?
(a) The electron will travel along a circle with constant speed and the proton will movealong a straight line
(b) Proton will move in a circle with constant speed and there will be no effect on the motion of electron
(c) There will not be any effect on the motion of electron and proton
(d) The electron and proton both will follow the path of a parabola
Ans. (b)
Q.14
An electron gun G emits electrons of energy 2 keV traveling in the positive X–direction. The electrons are required to hit the spot S, where GS = 0.1 m and line GS makes an angle of 60° with the X–axis as shown in figure. A uniform magnetic field \vec{B} parallel to G S exists in the region outside the electron gun. Find the minimum value of B needed to make the electron hit S.
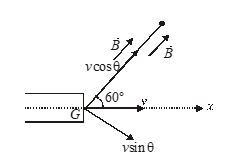
(a) 4.73\times {{10}^{{-3}}}T
(b) 4.73\times {{10}^{{-4}}}T
(c) 4.73\times {{10}^{{-5}}}T
(d) 4.73\times {{10}^{{-6}}}T
Ans. (a)
Q.15
A proton (mass m and charge +e) and \alpha –particle (mass 4 m and charge +2 e) are projected with the same kinetic energy at right angles to a uniform magnetic field. Which one of the following statements will be true?
(a) The \alpha –particle will be bent in a circular path with a smaller radius than proton
(b) The radius of the path of \alpha –particle will be greater than that of proton
(c) Radius of the paths of both the particles will be the same
(d) Both will go through the magnetic field in the straight
Ans. (c)
Practice Questions (JEE Advance Level)
Q.1
In a certain region uniform electric field E and magnetic field B are present in the opposite direction. At the instant t = 0 , a particle of mass m carrying a charge q is given velocity vo at an angle q, with the
y-axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to
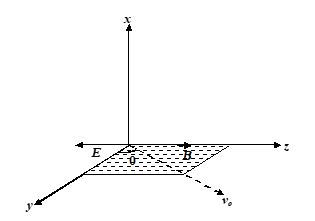
(a) \frac{{m{{v}_{o}}}}{{qE}}
(b) \frac{{m{{v}_{o}}\ \sin \theta }}{{qE}}
(c) \frac{{m{{v}_{o}}\ \cos \theta }}{{qE}}
(d) \frac{{2\pi m}}{{qB}}
Q.2
A particle of mass m, carrying a charge q, is lying at the origin in a uniform magnetic field directed along X axis. At the instant t = 0 it is given a velocity vo at an angle q with the y-axis, in the xy plane. The coordinates of the particle after one revolution will be
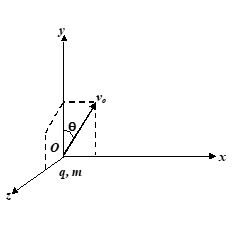
(a) \left( {0,\ 0\ \frac{{2\pi m{{v}_{o}}\ \sin \theta }}{{qB}}} \right)
(b) \left( {\frac{{2\pi m{{v}_{o}}\ \sin \theta }}{{qB}}\ ,\ 0\ ,\ 0} \right)
(c) \left( {\frac{{2\pi m{{v}_{o}}\ \sin \theta }}{{qB}},\ 0,\ 4} \right)
(d) (0, 0, 0)
Q.3
H+, He+ and O++ all having the same kinetic energy pass through a region in which there is a uniform magnetic field perpendicular to their velocity. The masses of H+, He+ and O++ are 1 amu, 4 amu and 16 amu respectively, then:
(a) H+ will be deflected most
(b) O++ will be deflected most
(c) He+ and O++ will be deflected equally
(d) All will be deflected equally
Q.4
Two long wires placed along x and y-axis carries equal currents in positive directions. An electron is projected with some initial velocity along the line x = y from the origin. The electron
(a) will be deflected towards x-axis
(b) will be deflected towards y-axis
(c) will describe a circle
(d) will not deflect at all
Ans : (d)
Q.5
A particle of specific charge q/m = p C/kg is projected from the origin towards positive
x-axis with a velocity of 10 m/s in a uniform magnetic field \vec{B}=-2\hat{k} T. The velocity \vec{V} of the particle after time t = \frac{1}{6} s will be
(a) \left( {5\hat{i}+5\sqrt{3}\,\hat{j}} \right) m/s
(b) 10\hat{j} m/s
(c) \left( {5\sqrt{3}\,\hat{i}-5\hat{j}} \right) m/s
(d) -10\hat{j} m/s
Ans : (a)
Q.6
A charged particle enters into a uniform magnetic field with velocity vo perpendicular to it, the length of magnetic field is x = \frac{{\sqrt{3}}}{2}R, where R is the radius of the circular path of the particle in the field. The magnitude of change in velocity of the particle when it comes out of the field is
(a) 2vo (b) vo/2 (c) \sqrt{3} vo/2 (d) vo
Ans : (d)
7.
A uniform electric field E is present horizontally along the paper throughout region but uniform magnetic field B0 is present horizontally (perpendicular to plane of paper in inward direction) right to the line AB as shown. A charge particle having charge q and mass m is projected vertically upward and crosses the line AB after time t0. Find the speed of projection if particle moves after t0 with constant velocity. (given qE = mg)
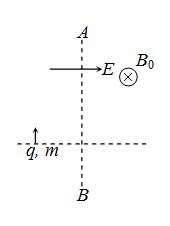
(a) gt0
(b) 2gt0
(c) \frac{{g{{t}_{0}}}}{2}
(d) particle can’t move with constant velocity after crossing AB
Ans (b)
