Video Lecture
Theory For Making Notes
CHARGE
Charge is a property of matter that causes it to produce and experience electrical and magnetic effects. The subject of the electrical effect of charges at rest is called electrostatics. When both electrical and magnetic effect are present, the interaction between charges is referred to as electromagnetic.
There exist two types of charges in nature: positive and negative. Like charges repel, and unlike charges attract.
The SI unit of charge is the coulomb (C). It is defined in terms of electric current. One coulomb is the charge transferred in one second across the section of wire carrying a current of one ampere.
q = It
⇒ 1C = (1A) (1s)
The reason is that one can make precise measurements of the current flowing in wire, whereas the charge on a body tends to leak away.
The coulomb is a very large amount of charge. A typical charge acquired by a rubbed body is 10–8C, whereas a lightning bolt may transfer as much as 20 C between the earth and a cloud.
Quantization of Charge
Electric charges appear only in discrete amounts, it is said to be quantized. The quantum of charge, first directly measured in 1909 by R. A. Millikan, is approximately
e = 1.602 x 10–19 C
A charge q must be an integer multiple of this basic unit. That is q = 0, ±e, ±2e, ±3eetcAlthough the mass of the proton is about 1800 times greater than that of the electron, their charges have the same magnitude.
qe = –e ; qp = + e
Note that the electron itself is not the charge: Charge is a property, like mass, of elementary particles, such as the electron.
Conservation of Charge
For an isolated system, the total charge remains constant, charge is neither created nor destroyed, it is transferred from one body to the other.
By ‘isolated’ we mean that there are no paths, such as wires or damp air, by which charges can leave or enter the system. To apply the law of conservation of charges, we add up the number of elementary charges before the interaction and then again after it. For example,
In a chemical reaction
Na+ + Cl– → NaCl
(+e) + (-e) = (0)
In a radioactive decay
n → p + e– + \bar{\nu } (antineutrino)
(0) = (+e) + (-e) + (0)
Invariance of Charge
The numerical value of an elementary charge is independent of velocity. It is provided by the fact that an atom is neutral. The difference in masses of an electron and a proton suggests that electrons move much faster in an atom than protons. If the charges were dependent on velocity, the neutrality of atoms would be violated.
Comparison of charge and mass
Charge | Mass |
(1) Electric charge can be positive, negative or zero | (1) Mass of a body is a positive quantity. |
(2) Charge carried by a body does not depend upon velocity of the body. | (2) Mass of a body increases with its velocity as m=\frac{{m{}_{0}}}{{\sqrt{{1-{{v}^{2}}/{{c}^{2}}}}}} where c is velocity of light in vacuum, m is the mass of the body moving with velocity v and m{}_{0} is rest mass of the body. |
(3) Charge is quantized. | (3) The quantization of mass is yet to be established. |
(4) Electric charge is always conserved. | (4) Mass is not conserved as it can be changed into energy and vice-versa. |
(5) Force between charges can be attractive or repulsive, accordingly as charges are unlike or like charges. | (5) The gravitational force between two masses is always attractive. |
Conductors and Insulators
In conductors charges are free to move throughout its volume whereas in insulators or dielectrics, the charges remain fixed at the places where they were initially distributed.
A body can be charged in the following ways:
- Charging by friction
When a glass rod is rubbed with silk, due to friction there is transfer of electrons from the rod to silk and hence rod becomes positively charged and silk negatively charged.
- Charging by Induction
There are following steps to charge a metal sphere by induction:
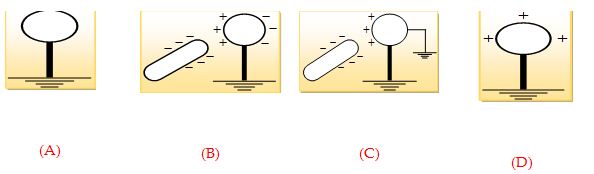
(A)
The metal sphere is supported on an insulated stand.
(B)
A negatively charged rod is brought near to it, without touching, then the free electrons in the metal sphere are repelled by the excess of electrons of the rod and the left surface accumulates positive charges.
(C)
The surface of the sphere is earthed using a wire and the negative charged flows to earth.
(D)
The wire is disconnected and the rod is removed.
Important Points
(i)
The rod (inducing body) neither gains nor loses charge.
(ii)
If the rod is negatively charged the sphere attains positive charge e. nature of induced charge is always opposite to that of inducing charge.
(iii)
Remember that induced charge can never be greater than the inducing charge.
- Charging by Conduction
When a charged body touches a neutral body, some charge is transferred from charged body to neutral body. Even on removing the charged body, the neutral body remains charged.
Note
The neutral body will have the same type of charge as charged body after conduction
COULOMB’S LAW
The force of interaction of two stationary point charges in vacuum is directly proportional to the product of these charges and inversely proportional to the square of their separation
F = \frac{{k{{q}_{1}}{{q}_{2}}}}{{{{r}^{2}}}} (1)
where k is a constant which depends on the system of units. Its value in SI unit is
k = 9 x 109 Nm2C-2
The constant is often written in the form
k = \frac{1}{{4\pi {{\varepsilon }_{0}}}}
wheree0 is called the permitivity constant which is numerically equal to
εo = 8.85 x 10-12 C2 /Nm2
The coulomb force acts along the straight line joining the points of location of the charges. This force is central and spherically symmetric.
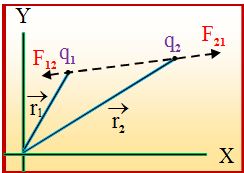
The vector form of Coulomb’s law is {{\vec{F}}_{{12}}}= \frac{{k{{q}_{1}}{{q}_{2}}}}{{{{r}^{2}}}}{{\hat{r}}_{{12}}} where {{\hat{r}}_{{12}}} is the unit vector, directed from q2 to q1and {{\vec{F}}_{{12}}} is the force on the charge q1due to q2. The same equation can be rewritten as
\displaystyle \overrightarrow{{{{F}_{{12}}}}}\,\,\,=\,\,\frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\,\frac{{{{q}_{1}}{{q}_{2}}}}{{|\overrightarrow{{{{r}_{1}}}}-\overrightarrow{{{{r}_{2}}}}{{|}^{3}}}}\,\,\,(\overrightarrow{{{{r}_{1}}}}-\overrightarrow{{{{r}_{2}}}})
Similarly force on charge q2due to q1is {{\vec{F}}_{{21}}}.
{{\vec{F}}_{{21}}} = \frac{{k{{q}_{1}}{{q}_{2}}}}{{{{r}^{2}}}}\left( {-{{{\hat{r}}}_{{12}}}} \right)
or \displaystyle \overrightarrow{{{{F}_{{21}}}}}\,\,\,=\,\,\frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\,\frac{{{{q}_{1}}{{q}_{2}}}}{{|\overrightarrow{{{{r}_{2}}}}-\overrightarrow{{{{r}_{1}}}}{{|}^{3}}}}\,\,\,(\overrightarrow{{{{r}_{2}}}}-\overrightarrow{{{{r}_{1}}}})
Important points regarding Coulomb’s law
1.
Charges are assumed to be at rest.
When charges are in motion they also produce and experience magnetic forces.
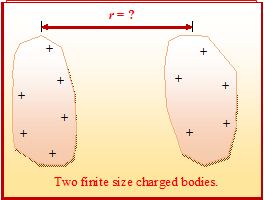
2.
Charges are assumed to be on point particles.
Coulomb’s law cannot be applied directly to a finite charge distribution.
There is an exception: when the charge is distributed uniformly over a spherical surface, the force on a point charge outside the surface may be computed from Coulomb’s law by treating the charge on the sphere as if it were concentrated at the centre. For charged body of finite size, there is no well-defined value of the separation r, integration is required.
Principle of Superposition
The coulomb’s law obeys the principle of superposition, which means that the force between two particles is not affected by the presence of other charges. This principle is used to find the net force exerted on a given particle by other charged particles.
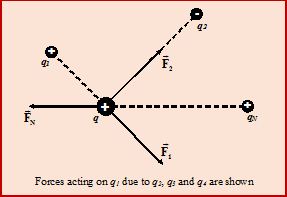
Consider N point charges 1, 2, ….., N with scalar magnitudes q1, q2,……..qN having position vectors \displaystyle \overrightarrow{{{{r}_{1}}}},\,\,\overrightarrow{{{{r}_{2}}}},\,\,\,\overrightarrow{{{{r}_{3}}}},……..\overrightarrow{{{{r}_{N}}}}, respectively, from some fixed origin O. The force exerted on the charge q located at \displaystyle \overrightarrow{r} by these charges is obtained by summing vectorially the forces by individual charges. So the net force on q is given by
{{\vec{F}}_{q}}={{\vec{F}}_{1}}+{{\vec{F}}_{2}}+….+{{\vec{F}}_{N}}
\displaystyle \overrightarrow{{{{F}_{q}}}}\,=\,q\,\,\sum\limits_{{i\,=\,1}}^{N}{{\frac{{{{q}_{i}}}}{{4\pi {{\varepsilon }_{0}}}}\,\,}}\,\frac{{(\overrightarrow{r}-\overrightarrow{{{{r}_{i}}}})}}{{|\overrightarrow{r}-\overrightarrow{{{{r}_{i}}}}{{|}^{3}}}}
Comparison with Gravitation Law
Coulomb’s law is analogous to Newton’s law of gravitation :
F = G \frac{{{{m}_{1}}{{m}_{2}}}}{{{{r}^{2}}}}
However, following are the important differences :
(a) Electric force between charged particles is much stronger than gravitational force,
i.e., FE>>FG. This is why when both FEand FG are present, we neglect FG
(e.g. between two electrons FG = 10–39FE).
(b) Electric force can be attractive or repulsive. But the gravitational force is always attractive.
(c) Electric force depends on the nature of medium between the charges, but gravitational force does not.
How to solve a problem using Coulomb’s law ?
1.
Decide whether the force due to a given charge is attractive or repulsive and express it by drawing vectors.
2.
Find the magnitude of the force using Coulomb’s law –ignoring the signs of the charges.
3.
Resolve the forces along the given co-ordinate axes and express them in vector form using \hat{i}, \hat{j} , \hat{k} unit vector notation unless otherwise specified.
4.
Use the principle of superposition to find the net force on a charge.
Illustration
Four point positive charges q are located at the corners of a square as shown in the figure. Find the net force acting on the charge at D.
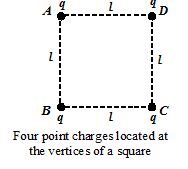
Solution
F={{\vec{F}}_{{DA}}}+{{\vec{F}}_{{DB}}}+{{\vec{F}}_{{DC}}}=\frac{{k{{q}^{2}}}}{{{{l}^{2}}}}\hat{i}+\frac{{k{{q}^{2}}}}{{{{l}^{2}}}}\hat{j}+\frac{{k{{q}^{2}}}}{{2{{l}^{2}}}}\left( {\cos {{{45}}^{o}}\,\hat{i}+\sin {{{45}}^{o}}\,\hat{j}} \right)
\vec{F}=\left( {1+\frac{1}{{2\sqrt{2}}}} \right)\frac{{k{{q}^{2}}}}{{\,{{l}^{2}}}}\hat{i}+\left( {1+\frac{1}{{2\sqrt{2}}}} \right)\frac{{k{{q}^{2}}}}{{\,{{l}^{2}}}}\hat{j}
|\vec{F}|=\sqrt{2}\left( {1+\frac{1}{{2\sqrt{2}}}} \right)\frac{{k{{q}^{2}}}}{{\,{{l}^{2}}}}
F=\left( {\frac{{2\sqrt{2}+1}}{2}} \right)\frac{{k{{q}^{2}}}}{{{{l}^{2}}}}
Illustration
A matter has a charge of +32 mC. How many electrons have been added or removed form it ?
Solution
Positive charge means electrons have been removed from the system and the number of removed electrons is
\displaystyle n=\frac{q}{e} \displaystyle =\frac{{32\times {{{10}}^{{-6}}}}}{{1.6\times {{{10}}^{{-19}}}}}=2\times {{10}^{{+14}}}
Illustration
Three point charges are placed at the following points on the x axis: q1 = + 2 µC atx = 0,q2 = –3µC atx = 40 cm, q3 = –5 µC atx = 120 cm. Find the force on the –3 µC charge.
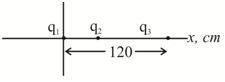
Solution
Figure is diagram of the setup with q1 = 2µC, q2 = –3µC, and q3 = –5µC. The force on q2 is the vector sum of two contributions, the attractive force due to q1 (toward q1), and the repulsive force due to q3 (also toward q1). The sum of these two forces, taken algebraically, since they are along the same line, is
\displaystyle F={{F}_{1}}-{{F}_{2}}=\frac{{-k|{{q}_{1}}{{q}_{2}}|}}{{{{{(0.40)}}^{2}}}}+\frac{{k|{{q}_{2}}{{q}_{3}}|}}{{{{{(0.80)}}^{2}}}}
\displaystyle =-9\times {{10}^{9}}\left[ {\frac{{(2\times {{{10}}^{{-6}}}C)\,\,(3\times {{{10}}^{{-6}}}C)}}{{{{{(0.40m)}}^{2}}}}+\frac{{(5\times {{{10}}^{{-6}}}C)\,\,(3\times {{{10}}^{{-6}}}C)}}{{{{{(0.80m)}}^{2}}}}} \right]=-0.55\text{N}
or 0.55 N to left.
Illustration
Two identical positive charges of magnitude Q are separated by a distance d. Another charge q is placed midway on the line joining the two. Identify the magnitude and nature of the charge q so that the system is in equilibrium
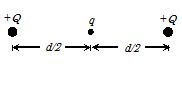
Solution
Since the charge q is placed symmetrically between the two Q charges, therefore, it is in equilibrium.
Let us check the equilibrium of any of the +Q charges.
Thus, \frac{{k{{Q}^{2}}}}{{{{d}^{2}}}}+\frac{{kQq}}{{{{{\left( {d/2} \right)}}^{2}}}}=0
or q=-\frac{Q}{4}
The charge q is a negative charge.
Note
The equilibrium of the system is unstable. If any of the three charges is slightly displaced along the line joining them, then the system does not restore the equilibrium.
Illustration
Four point charges are located at the corners of a rectangle, as shown in figure. Find the net force acting on the charge q1.
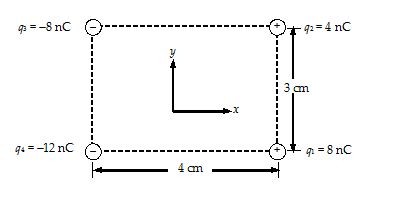
Solution
(1)
The force {{\vec{F}}_{{12}}} (between q1 and q2) is repulsive, while the forces {{\vec{F}}_{{13}}} (between q1 and q3) and {{\vec{F}}_{{14}}} (between q1 and q4) are attractive.
(2)
The magnitude of the forces {{\vec{F}}_{{12}}} , {{\vec{F}}_{{13}}} and {{\vec{F}}_{{14}}} are
\displaystyle {{\text{F}}_{{\text{12}}}}=\text{ }\frac{{k{{q}_{\text{1}}}{{q}_{2}}}}{{r_{{12}}^{2}}}\text{ }=\text{ }\frac{{\left( {\text{9 }\times \text{ 1}{{\text{0}}^{\text{9}}}} \right)\text{ }\left( {\text{8 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)\text{ }\left( {\text{4 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)}}{{\text{ }{{{\left( {\text{3 }\times \text{ 1}{{\text{0}}^{{\text{-2}}}}} \right)}}^{2}}}}\text{ }=\text{ 32 }\times \text{ 1}{{\text{0}}^{{\text{-5}}}}\text{N}
\displaystyle {{\text{F}}_{{\text{13}}}}\text{ }=\text{ }\frac{{k{{q}_{\text{1}}}{{q}_{3}}}}{{r_{{13}}^{2}}}\text{ }=\text{ }\frac{{\left( {\text{9 }\times \text{ 1}{{\text{0}}^{\text{9}}}} \right)\text{ }\left( {\text{8 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)\text{ }\left( {\text{8 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)}}{{\text{ }{{{\left( {\text{5 }\times \text{ 1}{{\text{0}}^{{\text{-2}}}}} \right)}}^{2}}}}\text{ }=\text{ 23 }\times \text{ 1}{{\text{0}}^{{\text{-5}}}}\text{N}
\displaystyle {{\text{F}}_{{\text{14}}}}\text{ }=\text{ }\frac{{k{{q}_{\text{1}}}{{q}_{4}}}}{{r_{{14}}^{2}}}\text{ }=\text{ }\frac{{\left( {\text{9 }\times \text{ 1}{{\text{0}}^{\text{9}}}} \right)\text{ }\left( {\text{8 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)\text{ }\left( {\text{12 }\times \text{ 1}{{\text{0}}^{{\text{-9}}}}} \right)}}{{\text{ }{{{\left( {\text{4 }\times \text{ 1}{{\text{0}}^{{\text{-2}}}}} \right)}}^{2}}}}\text{ }=\text{ 54 }\times \text{ 1}{{\text{0}}^{{\text{-5}}}}\text{N}
(3)
{{\vec{F}}_{{12}}} = (-32 x 10–5) \hat{j}
{{\vec{F}}_{{13}}} = (F13cos q) \hat{i} + (F13 sin q) \hat{j} = \displaystyle \left[ {-\text{(23) }\left( {\frac{\text{4}}{\text{5}}} \right)\text{ }\hat{i}\text{ }+\text{ (23) }\left( {\frac{\text{3}}{\text{5}}} \right)\text{ }\hat{j}} \right]\times \text{ 1}{{\text{0}}^{{\text{-5}}}}
= [-18.4 \hat{i} + 13.8 \hat{j}] x 10–5
{{\vec{F}}_{{14}}} = (–54 x 10–5) \hat{i}
(4)
The net force on q1 is \displaystyle {{\vec{F}}_{1}}={{\vec{F}}_{{12}}}+{{\vec{F}}_{{13}}}+{{\vec{F}}_{{14}}}
= [-72.4 \hat{i} -18.2 \hat{j}] x 10–5 N
Illustration
Two points charges + 8q and –2q are located at x = 0 and x = L respectively. The location of a point on the x-axis at which the net force on a third charge due to these two point charges is zero
(a) 2 L
(b) L/4
(c) 8L
(d) 4
Solution
Let the third charge is Q and placed at a distance x from 8q charge. Net force on it will be zero only if the forces due to +8q and -2q cancel each other.
\displaystyle \frac{{2qQ}}{{4\pi {{\varepsilon }_{0}}{{{(x-L)}}^{2}}}}=\frac{{8qQ}}{{4\pi {{\varepsilon }_{0}}{{x}^{2}}}} orx = 2L Ans. (a)
Illustration
When two charges are equal q each, force they exert on each other is F. When one of the charge is doubled, the 2q charge exerts a force 2F on charge q. The force exerted by q on 2q is
(a) F
(b) F/2
(c) F/4
(d) 2F
Solution
Force is mutual. Ans. (d)
Illustration
The two balls shown in figure have identical masses of 0.20g each. When suspended from 50 cm long strings, they make an angle of 37° to the vertical. If the charges on each are the same, how large is each charge?
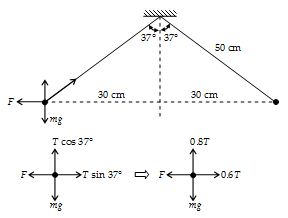
Solution
Since the system is at rest, we can apply the conditions for equilibrium to the ball on the left. Note that three forces act on the ball: its weight mg; the tension T in the string; and F, the repulsive force due to the charge on the other ball. Applying the condition for equilibrium ∑Fx = 0, we get
F – 0.6T = 0 … (1)
0.8 T – mg = 0 … (2)
From equation (1) and (2), we get
\displaystyle F=\frac{3}{4}mg=\frac{3}{4} (0.2 X 10–3 X 10) = 1.5 X 10–3N
From coulomb’s law. We have
\displaystyle F=\frac{{k{{q}^{2}}}}{{{{d}^{2}}}}=\frac{{(9\times {{{10}}^{9}}){{q}^{2}}}}{{{{{(0.60)}}^{2}}}}
Substituting the value of F in the above equation, we get
\displaystyle 1.5\times {{10}^{{-3}}}=(9\times {{10}^{9}})\frac{{{{q}^{2}}}}{{{{{(0.60)}}^{2}}}}
Solving for q, we find that \displaystyle q\approx 2.4\times {{10}^{{-7}}}C=0.24\mu C.
Illustration
A thin non-conducting ring of radius r has an electric charge +Q. A point charge +{{q}_{0}} is placed at the centre of the ring.
(a) Find the interaction force between the charged particle and the ring?
(b) Find the increase in tension of the wire ?
Solution
(a) At the center the field due to ring is zero. Hence, the force of interaction between the point charge +{{q}_{0}} and the ring is zero.
(b) The free body diagram of a small element of the ring is shown in fig.
It is clear from the equilibrium of the element
\displaystyle dF=2T\sin \frac{{d\,\theta }}{2}
= \frac{{k{{q}_{0}}(\lambda Rd\theta )}}{{{{R}^{2}}}}.
Since d\theta is very small \sin \frac{{d\,\theta }}{2} \frac{{d\,\theta }}{2}.
or \displaystyle 2T\frac{{d\theta }}{2}
=\frac{{k{{q}_{0}}(\lambda Rd\theta )}}{{{{R}^{2}}}}.
Hence T=\frac{{k{{q}_{0}}\lambda }}{R}.
Practice Questions (Basic Level)
Q.1
There are two charges +1 µC and +5µC. The ratio of the forces acting on them will be
(a) 1 : 5
(b) 1 : 1
(c) 5 : 1
(d) 1 : 25
Q.2
Two similar small spheres having +q and –q charge are kept at a certain distance. F force acts between the two. If in the middle of two spheres, another similar small sphere having +q charge is kept, then it will experience a force in magnitude and direction
(a) zero having no direction
(b) 8F towards +q charge
(c) 8F towards –q charge
(d) 4F towards +q charge
Q.3
The force between two charges 0.06m apart is 5N. If each charge is moved towards the other by 0.01m, then the force between them will become
(a) 7.20 N
(b) 11.25 N
(c) 22.50 N
(d) 45.00 N
Q.4
Two charged spheres separated at a distance d exert a force F on each other. If they are immersed in a liquid of dielectric constant 2, then what is the force (if all conditions are same)
(a) F/2
(b) F
(c) 2F
(d) 4F
Q.5
Two small conducting spheres of equal radius have charges +10 µC and –20 µC respectively and placed at a distance R from each other. They experience force F1. If they are brought in contact and separated to the same distance, they experience force F2. The ratio of F1 to F2 is
(a) 1 : 8
(b) –8 : 1
(c) 1 : 2
(d) –2 : 1
Q.6
Two equally charged, identical metal spheres A and B repel each other with a force F. The spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and then placed at the mid-point of the line joining A and B. The magnitude of the net electric force on C is
(a) F
(b) F/4
(c) F/2
(d) 4F
Q.7
A charge q is lying at mid-point of the line joining the two similar charges Q. The system will be in equilibrium if the value of q is
(a) Q/2
(b) -Q/2
(c) Q/4
(d) -Q/4
Q.8
A charge q1 exerts some force on a second charge q2. If a third charge q3 is brought near q2, the force exerted by q1 on q2
(a) decreases
(b) increases
(c) remains the same
(d) increases if q3 is of same sign as q1 and decreases if q3 is of opposite sign as q1
Q.9
Three equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
(a) 1/2
(b) 2
(c) 0.707
(d) 1.414
Q.10
A metallic sphere having no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the sphere will be
(a) towards the plate
(b) away from the plate
(c) parallel to the plate
(d) zero
Q.11
Two equally charged, identical metal spheres A and B repel each other with a force ‘F’. The spheres are kept fixed with a distance ‘r’ between them. A third identical, but uncharged sphere C is brought in contact with A and then placed at the mid-point of the line joining A and B. The magnitude of the net electric force on C is
(a) F/4
(b) 3F/4
(c) F/2
(d) F/4
Q.12
An infinite number of charges, each of charge 1 μC, are placed on the x-axis with co-ordinates x = 1, 2, 4, 8, ……… . If a charge of 1 C is kept at the origin, then what is the net force acting on 1 C charge
(a) 9000 N
(b) 12000
(c) 24000 N
(d) 36000 N
Q.13
Which of the following statement is correct?
(a) Charge is fundamental quantity.
(b) Charge can exist without mass
(c) Charge is independent of state of rest or motion.
(d) The whole charge on a body cannot be transferred to the other
Ans. (c)
Q.14
Two identical conductors, one of copper and the other of Aluminium are placed in an electric field. Assume copper is more conducting than aluminium.
(a) Induced charge is more in copper
(b) Induced charge is more in Aluminium
(c) Induced charge is equal in both the metals.
(d) Induced charge is zero in both the metals.
Ans. (c)
Q.15
Two points charge q1 and q2 are placed at a distance of 50 cm from each other in air, and interact with a certain force. Now the same charges are put in an oil whose relative permittivity is 5. If the interacting force between them is still the same, their separation now is
(a) 16. 6 cm
(b) 22.3 cm
(c) 28.4 cm
(d) 25.0 cm
Ans.(b)
Q.16
In Coulomb’s law, the force between two point charges is proportional to
1. the square of the distance between them
2. the product of the charges
3. the permittivity of the medium
(a) 1 and 2 only
(b) 1 and 3 only
(c) 2 and 3 only
(d) 2 only
Ans. (d)
Q.17
Force acting on a test charge between the plates of a parallel plate capacitor is F. If one of the plates is removed, then the force on the same test charge will be
(a) zero
(b) F
(c) 2F
(d) F/2
Ans. (d)
Q.18
A charge Q is fixed at each of two opposite corners of a square. A charge q is placed at each of the other two corners. If the resultant electrical force on Q is zero, then Q and q are related as
(a) Q = \sqrt{2}q
(b) Q = -2 \sqrt{2}q
(c) Q = \sqrt{2}{{q}^{2}}
(d) Q = -2 \sqrt{2}{{q}^{2}}
Ans. (b)
Q.19
A charge q1 exerts some force on a second charge q2. If a third charge q3 is brought near q2, the force exerted by q1 on q2
(a) decreases
(b) increases
(c) remains the same
(d) increases if q3 is of same sign as q1 and decreases if q3 is of opposite sign as q1
Ans. (c)
Q.20
A point charge Q is moved along a circular path around another fixed point charge. The work done is zero
(a) only if Q return to its starting point
(b) only if the two charges have the same magnitude
(c) only if the two charges have the same magnitude and opposite signs
(d) in all cases
Ans. (d)
Q.21
Two identical metal balls with charges +2Q and -Q are separated by some distance, and exert a force F on each other. They are joined by a conducting wire, which is then removed. The force between them will now be
(a) F
(b) F/2
(c) F/4
(d) F/8
Ans. (d)
Practice Questions (JEE Main Level)
Q.1
Three charged particles are in equilibrium under their electrostatic forces only.
(a) The particles must be collinear
(b) All the charges cannot have the same sign
(c) The equilibrium is unstable
(d) Both (b) and (c)
Ans. (d)
Q.2
A positively charged thin metal ring of radius r is fixed in the xy-plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0, 0, zo) where
zo > 0. Then the motion of P is
(a) periodic, for all values of zo satisfying 0 < zo < ¥
(b) simple harmonic, for all values of zo satisfying 0 < zo £ R
(c) approximately simple harmonic, provided zo =R
(d) such that P crosses O and continues to move along negative x-axis towards z = -¥.
Ans. (a)
Q.3
Two particles, each of mass m and carrying charge Q, are separated by some distance. If they are in equilibrium under mutual gravitational and electrostatic forces then Q/m (in C/kg)
(a) 10-5 (b) 10-10 (c) 10-15 (d) 10-20
Ans. (b)
Q.4
In the previous question, the equilibrium is
(a) stable
(b) unstable
(c) neutral
(d) may be any of the above depending on the separation of the particles.
Ans. (c)
Q.5
Three point charges are placed at the corners of an equilateral triangle. Assume that only electrostatic forces are acting.
(a) The system will be in equilibrium if the charges have the same magnitude but not all have the same sign.
(b) The system will be in equilibrium if the charges have different magnitudes and not all have the same sign.
(c) The system will be in equilibrium if the charges rotate about the centre of the triangle.
(d) The system can never be in equilibrium.
Ans. (d)
Q.6
Charge Q is divided into two parts which are then kept some distance apart. The force between them will be maximum it the two parts are
(a) Q/2 each
(b) Q/4 and 3Q/4
(c) Q/3 and 2Q/3
(d) e and (Q-e), where e=electronic charge
Ans. (a)
Q.7
Two identical pendulums, A and B, are suspended from the same point. The bobs are given positive charges, with A having more charge than B. They diverge and reach equilibrium, with A and B making angles q1 and 2 with the vertical respectively.
(a) q1>q2
(b) q1<q2
(c) q1=q2
(d) The tension in A is greater than that in B.
Ans. (c)
Q.8
A system consists of a thin charged wire ring of radius r and a very long uniformly charged wire oriented along the axis of the ring, with one of its ends coinciding with the center of the ring. The total charge on the ring is q, and the linear charge density on the straight wire is l. The interaction force between the ring and the wire is
(a) \displaystyle \frac{{\lambda q}}{{4\pi {{\varepsilon }_{0}}r}}
(b) \displaystyle \frac{{\lambda q}}{{2\sqrt{2}\pi {{\varepsilon }_{0}}r}}
(c) \displaystyle \frac{{2\sqrt{2}\lambda q}}{{\pi {{\varepsilon }_{0}}r}}
(d) \displaystyle \frac{{4\lambda q}}{{\pi {{\varepsilon }_{0}}r}}
Ans. (a)
Q.9
Two similar conducting balls of mass m are hung from silk threads of length L and carry similar charges q as shown in the figure. Assuming q to be small, the distance x between the balls is
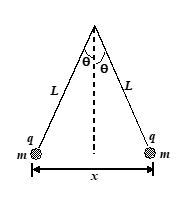
(a) {{\left[ {\frac{{{{q}^{2}}L}}{{4\pi {{\varepsilon }_{o}}mg}}} \right]}^{{1/3}}}
(b) {{\left[ {\frac{{{{q}^{2}}L}}{{2\pi {{\varepsilon }_{o}}mg}}} \right]}^{{1/3}}}
(c) {{\left[ {\frac{{{{q}^{2}}L}}{{4\pi {{\varepsilon }_{o}}mg}}} \right]}^{{3/2}}}
(d) {{\left[ {\frac{{{{q}^{2}}L}}{{2\pi {{\varepsilon }_{o}}mg}}} \right]}^{{1/2}}}
Ans. (b)
Q.10
An isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r >> l). When q1 is in equilibrium, tension in thread will be
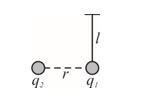
(a) \displaystyle mg
(b) \displaystyle >mg
(c) \displaystyle <mg
(d) None of these
Ans. (b)
10.
Two identical conducting spheres having unequal charges q1 and q2 separated by distance r. If they are made to touch each other and then separated again to the same distance. The electrostatic force between the spheres in this case will be (neglect induction of charges)
(a) less than before
(b) same as before
(c) more than before
(d) zero
Ans (c)
11.
A point charge + q is fixed at point B. Another point charge + q at A of mass m vertically above B at height h is dropped from rest. Choose the correct statement
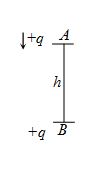
(a) It will collide with B
(b) It will execute S.H.M
(c) It will go down only if \frac{{{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}}}<mgh2
(d) go down up to a point and then come up
Ans (c)
12
Three point charges lie on a straight line, as shown in the figure. Find the resultant force exerted on 5 \displaystyle \mu C charge
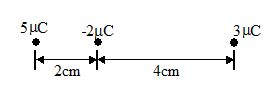
(a)-191 \hat{i} N;
(b) 188 \hat{i} N
(c)-156 \hat{i} N
(d) 135 \hat{i} N
Ans : (b)
13.
Three point charges are held on the corners of an equilateral triangle as shown in the figure. Take Q = 2 \displaystyle \mu C and
L = 3 cm. What is the resultant force exerted on the charge +3Q
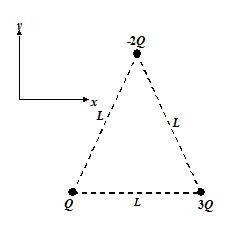
(a) 208 \hat{j}N
(b) (80 \hat{i}-27 \hat{j}) N
(c) 500 \hat{j}
(d) 300 \hat{j}
Ans (a)
14.
A point charge –Q is located at (0,-a) and charge +Q is at (0, a)Find At what point is the force on a charge q at (x, 0) be maximum
(a) \displaystyle x=\pm \frac{a}{{\sqrt{2}}}
(b) x = 0
(c) x = +9
(d) x = -9
ans : (b)
Practice Questions (JEE Advance Level)
Q.1
Two small identical balls lying on a horizontal plane are connected by a weightless-spring. One ball (ball 2) is fixed and the other (ball 1) is free. The balls are charged identically as a result of which the spring length increases 2 times. Determine the change in frequency.
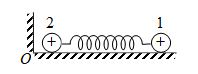
Ans. \Delta f=(\sqrt{2}-1) times
Q. 2
The force experienced by the semicircular rod charged with a charge q, placed as shown in figure will be (Radius of the wire is R and the line of charge with linear charge density l is passing through its centre and perpendicular to the plane of wire).
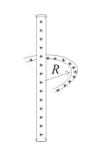
(a) \frac{{\lambda q}}{{2{{\pi }^{2}}{{\varepsilon }_{0}}R}}
(b) \frac{{\lambda q}}{{{{\pi }^{2}}{{\varepsilon }_{0}}R}}
(c) \frac{{\lambda q}}{{4{{\pi }^{2}}{{\varepsilon }_{0}}R}}
(d) \frac{{\lambda q}}{{4\pi {{\varepsilon }_{0}}R}}
Ans. (b)
Q.3
Two infinitely long wires having linear charge densities l1 and l2 are placed perpendicular to each other as shown in the figure. The force of interaction between them is proportional to
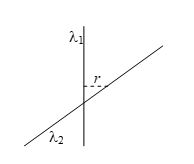
(a) r
(b) r2
(c) r3
(d) does not depend on r
Ans. (d)
Q.4
Four equal charges are kept fixed on the vertices of a square of side ‘a’. A charge is kept at the centre of the square as shown in the figure. Then
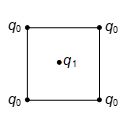
(a) charge is always in stable equilibrium
(b) charge cannot be in stable equilibrium
(c) charge is always in stable equilibrium only if and the charges on the vertices of the square have different signs
(d) charge is always in stable equilibrium only if and the charges on the vertices of the square have same signs
Ans. (b)
Q. 5
A charged particle having some mass is resting in equilibrium at a height H above the centre of a uniformly charged non‑conducting horizontal ring of radius R. The force of gravity acts downwards. The equilibrium of the particle will be stable
(a) for all values of H
(b) only if H > \frac{R}{{\sqrt{2}}}
(c) only if H < \frac{R}{{\sqrt{2}}}
(d) only if H = \frac{R}{{\sqrt{2}}}
Ans. (b)
Q.6
Three point charges, each with charge q and mass ‘m’, are connected by three strings of equal length ‘l’ whose other end is connected to a fixed point P. They form an equilateral triangle of side ‘a’ in a horizontal plane. The tension in each string will be
(a) \sqrt{{{{{(mg)}}^{2}}-{{{\left( {\frac{{{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{a}^{2}}}}\sqrt{3}} \right)}}^{2}}}}
(b) \frac{{mgl}}{{\sqrt{{{{l}^{2}}-{{a}^{2}}/3}}}}
(c) \frac{{3{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{a}^{2}}}}
(d) None of these
Ans. (b)
Q.7
Two positive point charges of magnitude Q each are separated by a distance “2a”. A test charge ‘{{q}_{0}}’ is located in a plane which is normal to the line joining these charges and midway between them. The locus of the points in this plane for which the force on the test charge has a maximum value is
(a) a circle of radius r=a/\sqrt{2}
(b) a circle of radius r=a
(c) a straight line
(d) an ellipse
Ans. (a)
Q.8
Three point charges, each with charge q and mass ‘m’, are connected by three strings of equal length ‘l’ whose other end is connected to a fixed point P. They form an equilateral triangle of side ‘a’ in a horizontal plane. The tension in each string will be
(a) \sqrt{{{{{(mg)}}^{2}}-{{{\left( {\frac{{{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{a}^{2}}}}\sqrt{3}} \right)}}^{2}}}}
(b) \frac{{mgl}}{{\sqrt{{{{l}^{2}}-{{a}^{2}}/3}}}}
(c) \frac{{3{{q}^{2}}}}{{4\pi {{\varepsilon }_{0}}{{a}^{2}}}}
(d) None of these
Ans. (b)
Q.9
Four equal charges are kept fixed on the vertices of a square of side ‘a’. A charge {{q}_{1}} is kept at the centre of the square as shown in the figure. Then
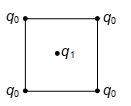
(a) charge {{q}_{1}} is always in stable equilibrium
(b) charge {{q}_{1}} cannot be in stable equilibrium
(c) charge {{q}_{1}} is always in stable equilibrium only if {{q}_{1}} and the charges on the vertices of the square have different signs
(d) charge {{q}_{1}} is always in stable equilibrium only if {{q}_{1}} and the charges on the vertices of the square have same signs
Ans. (b)
10.
Figure shows five point charges along a straight line. The separation between the charges is 1 cm. Find for what values of q1and q2would the net force on each of the other three charges be zero ?
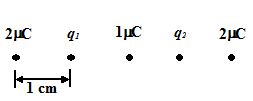
(a) – \frac{{32}}{{80}} µC
(b) – \frac{{27}}{{80}}µC
(c) – \frac{{50}}{{80}} µC
(d) – \frac{{32}}{{50}} µC
Ans (b)
11.
A thin fixed ring of radius 1 m has a positive charge 1´10–5 C uniformly distributed over it. A particle of mass 0.9 g and having a negative charge of 1´10–6 C is placed on the axis at a distance of 1 cm from the centre of the ring. Show that the motion of the negatively charged particle is approximately simple harmonic. Calculate the time period of oscillations.
(a) \displaystyle \pi /8 second
(b) \displaystyle \pi /5 second
(c) \displaystyle \pi /4 second
(d) \displaystyle \pi /2 second
Ans (b)
