Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-2)
1.
In the Young’s double slit experiment apparatus shown in figure, the ratio of maximum to minimum intensity on the screen is 9. The wavelength of light used is \displaystyle \lambda , then the value of y is :
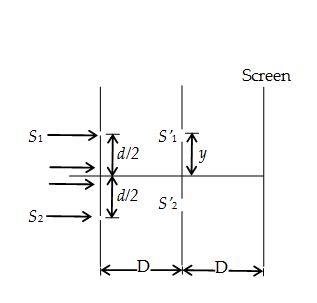
(a) \displaystyle \frac{{\lambda D}}{d}
(b) \displaystyle \frac{{\lambda D}}{{2d}}
(c) \displaystyle \frac{{\lambda D}}{{3d}}
(d) \displaystyle \frac{{\lambda D}}{{4d}}
Ans (c)
2.
The maximum intensity in Young’s double slit experiment is Io. Distance between the silts is d = 5 \displaystyle \lambda , where \displaystyle \lambda is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance D = 10 d?
(a) \displaystyle \frac{{{{I}_{o}}}}{2}
(b) \displaystyle \frac{3}{4}{{I}_{o}}
(c) \displaystyle {{I}_{o}}
(d) \displaystyle \frac{{{{I}_{o}}}}{4}
Ans (a)
3.
When one of the slits of Young’s experiment is covered with a transparent sheet of thickness 4.8 mm, the central fringe shifts to a position originally occupied by the 30th bright fringe. What should be the thickness of the sheet if the central fringe has to shift to the position occupied by 20th bright fringe?
(a) 3.8 mm
(b) 1.6 mm
(c) 7.6 mm
(d) 3.2 mm
Ans (d)
4.
In the ideal double-slit experiment, when a glass plate ( \displaystyle \mu = 1.5) of thickness t is introduced in the path of one of the intersecting beams (wavelength \displaystyle \lambda ) the intensity at the position where the central maximumoccurred previously remains unchanged. The minimum thickness of the glass plate is?
(a) 2 \displaystyle \lambda
(b) 2 \displaystyle \lambda /3
(c) \displaystyle \lambda /3
(d) \displaystyle \lambda
Ans (a)
5.
In the Young’s double slit experiment a point P on the central bright fringe is such that intensity of point P is 1/4 times the maximum intensity, distance between the slits is d and wavelength \displaystyle \lambda . Then angular separation of point P is
(a) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{d}} \right)
(b) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{2d}}} \right)
(c) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{3d}}} \right)
(d) \displaystyle {{\sin }^{{-1}}}\left( {\frac{\lambda }{{4d}}} \right)
Ans (c)
6.
In an interference arrangement similar to Young’s double-slit experiment, the slits and are illuminated with coherent microwave sources, each of frequency Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0m. The intensity I\left( \theta \right) is measured as a function of \theta , where \theta is defined as shown. If {{I}_{0}} is the maximum intensity, then I\left( \theta \right) for 0\le \theta \le 90{}^\circ is given by
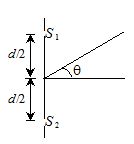
(a) I\left( \theta \right)={{I}_{0}}/2for \theta =30{}^\circ
(b) I\left( \theta \right)={{I}_{0}}/4for \theta =90{}^\circ
(c) I\left( \theta \right)={{I}_{0}}for \theta =0{}^\circ
(d) I\left( \theta \right)is constant for all values of \theta
Ans (b)
7.
In a double slit experiment instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
(a) the intensities of both the maxima and the minima increase
(b) the intensity of the maxima increases and the minima has zero intensity
(c) the intensity of the maxima decreases and that of the minima increases
(d) the intensity of the maxima decrease and the minima has zero intensity
Ans (d)
8.
Two beams of light having intensities I and \displaystyle 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is \pi /2 at point and \pi at point . Then the difference between the resultant intensities at and is
(a) \displaystyle 4I
(b) \displaystyle 4I
(c) \displaystyle 5I
(d) \displaystyle 7I
Ans (c)
9.
In a Young’s double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600 nm is used. If the wavelength of light is changed to 400 nm, number of fringes observed in the same segment of the screen is given by
(a) 12
(b) 18
(c) 24
(d) 30
Ans (d)
10.
White light is used to illuminate the two slits in Young’s Double Slit experiment. The separation between the slits is b and the screen is at a distance d(>> b) from the slits. At a point on the screen directly in front of any of the slits, certain wavelength are missing. Some of these missing wavelength are
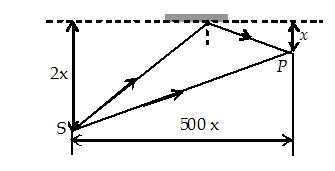
(a) \displaystyle \lambda \,=\,\frac{{{{b}^{2}}}}{d}
(b) \displaystyle \lambda \,=\,\frac{{{{b}^{2}}}}{{3d}}
(c) Both (a) and (b)
(d) \displaystyle \lambda \,=\,\frac{{2{{b}^{2}}}}{{3d}}
Ans (c)
11.
A thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown. The observed interference fringes from this combination shall be
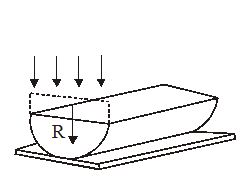
(a) straight
(b) circular
(c) equally spaced
(d) having fringe spacing which increases as we go outwards
Ans (d)
12.
In Young’s experiment, let P and Q be the two slits. A thin film of thickness t and refractive index n is placed in front of P. If \displaystyle \beta be the fringe width and \displaystyle \lambda be the wavelength of light then the central maxima will shift
(a) towards \displaystyle P\,\,\,by\,\,\,t(n1)\frac{\beta }{\lambda }
(b) towards \displaystyle Q\,\,by\,\,t(n1)\frac{\beta }{\lambda }
(c) towards \displaystyle P\,\,by\,\,nt\frac{\beta }{\lambda }
(d) towards \displaystyle Q\,\,by\,\,nt\frac{\beta }{\lambda }
Ans (a)
13.
Light of wavelength \displaystyle {{\lambda }_{0}}in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference \displaystyle {{\varnothing }_{0}} between these two points is
(a) \displaystyle {{\phi }_{0}}\,=\,\frac{1}{n}\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(b) \displaystyle {{\phi }_{0}}\,=\,n\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(c) \displaystyle {{\phi }_{0}}\,=\,(n1)\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
(d) \displaystyle {{\phi }_{0}}\,=\,\frac{1}{{(n1)}}\,\left( {\frac{{2\pi }}{{{{\lambda }_{0}}}}} \right)\,x
Ans (b)
14.
In Young’s double slit experiment, the slits are 2 mm apart and are illuminated with a mixture of two wavelengths \displaystyle {{\lambda }_{o}}\,=\,750\,nm\,\,\,and\,\,\lambda \,=\,900\,nm. The minimum distance from the common central bright fringe on a screen 2 m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
(a) 1.5 mm
(b) 3 mm
(c) 4.5 mm
(d) 6 mm
Ans (c)
15.
In the ideal double slit experiment, when a glass plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength \displaystyle \lambda ) the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass plate is
(a) 2 \displaystyle \lambda
(b) \displaystyle \frac{{2\lambda }}{3}
(c) \displaystyle \frac{\lambda }{3}
(d) \displaystyle \lambda
Ans (a)
16.
Two wavelengths of light \displaystyle {{\lambda }_{1}} and \displaystyle {{\lambda }_{2}} are sent through a Young’s double slit apparatus simultaneously. If the third order l1 bright fringe coincides with the fourth order \displaystyle {{\lambda }_{2}}bright fringe then
(a) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{4}{3}
(b) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{3}{4}
(c) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{5}{4}
(d) \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,=\,\frac{4}{5}
Ans (a)
17.
Two identical sources each of intensity Iohave a separation \displaystyle d\,=\,\frac{\lambda }{8}, where \displaystyle \lambda is the wavelength of the waves emitted by either source. The phase difference of the sources is \displaystyle \frac{\pi }{4}. The intensity distribution I(q) in the radiation filed as a function of[ \displaystyle \theta ], which specifies the direction from the sources to the distant observation point P is given by
(a) \displaystyle I\,(\theta )\,=\,{{I}_{o}}\,{{\cos }^{2}}\,\theta
(b) \displaystyle I\,(\theta )\,=\,\frac{{{{I}_{o}}}}{4}\,{{\cos }^{2}}\,\left( {\frac{{\pi \theta }}{8}} \right)
(c) \displaystyle I\,(\theta )\,=\,4{{I}_{o}}{{\cos }^{2}}\,\left( {\frac{\pi }{8}\,(\sin \theta \,+\,1)} \right)
(d) \displaystyle I\,(\theta )\,=\,{{I}_{o}}{{\sin }^{2}}\,\theta
Ans (c)
18.
In a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other. Then in the interference pattern
(a) the intensities of both the maxima and the minima increase
(b) the intensity of the maxima increases and minima has zero intensity
(c) the intensity of the maxima decreases and that of minima increases
(d) the intensity of the maxima decreases and the minima has zero intensity
Ans (a)
19.
In a Fresnel biprism set-up, l is the distance of the prism from the source slit, A is the angle of the prism and \displaystyle \mu is the refractive index of the material of the prism. Then the separation between the two virtual sources will be equal to
(a) lA ( \displaystyle \mu – 1)/2
(b) 2lA ( \displaystyle \mu – 1)
(c) 3lA ( \displaystyle \mu – 1)
(d) 4lA( \displaystyle \mu – 1)
Ans (c)
20.
Consider a usual set up of Young’s double slit experiment with slits of equal intensity as shown in the figure. Take ‘O’ as origin and the Y axis as indicated. If average intensity between y1 = – \displaystyle \frac{{\lambda D}}{{4d}} and y2 = + \displaystyle \frac{{\lambda D}}{{4d}} equals ‘n’ times the intensity of maxima, then ‘n’ equals
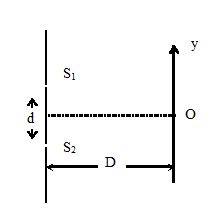
(a) \displaystyle \frac{1}{2}\left( {1+\frac{2}{\pi }} \right)
(b) \displaystyle 2\left( {1+\frac{2}{\pi }} \right)
(c) \displaystyle \left( {1+\frac{2}{\pi }} \right)
(d) \displaystyle \frac{1}{2}\left( {1-\frac{2}{\pi }} \right)
Ans (a)
21.
In a Young’s double slit experiment, the fringes are displaced by a distance ‘x’ when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
(a) 1.75
(b) 1.50
(c) 1.25
(d) 1.00
Ans (c)
22.
Which of the following is not an essential condition for interference
(a) The two interfering waves must be propagated in almost the same direction or the two interfering waves must intersect at very small angle
(b) The waves must have the same period and wavelength
(c) The amplitude of the two waves must be equal
(d) The two interfering beams of light must originate from the same source
Ans (c)
23.
To demonstrate the phenomenon of interference we require
(a) two sources which emit radiation’s of the same frequency
(b) two sources which emit radiations of nearly the same frequency
(c) two sources which emit radiations of the same frequency and have a definite phase relationship
(d) two sources which emit radiations of different frequencies
Ans (c)
24.
A bright fringe in Young’s double-slit experiment is 1.5 cm from the center of the pattern. The light has a wave length of 612 nm and falls on a screen 1.4 m from the slits, whose separation is 0.4 mm. How many dark fringes are there between the center and the bright fringe at 1.5 cm?
(a)5 fringes
(b)7 fringes
(c)10 fringes
(d)2 fringes
Ans (b)
25.
Light of wavelength 627 nm illuminates two slits. What is the minimum path difference between the waves from the slits for the resultant intensity to fall to 25% of the central maximum?
(a)200nm
(b)205 nm
(c)209 nm
(d)215 nm
Ans (c)
26.
In a Young’s double slit experiment, two wavelengths of 500 nm and 700 nm were used. What is the minimum distance from the central maximum where their maximas coincide again? Take D/d = 103. Symbols have their usual meanings.
(a)5.0 mm
(b)3.5 mm
(c)2.0 mm
(d)3.0 mm
Ans (b)
