Video Lecture
Theory For Making Notes
Energy
Energy of a body is its capacity of doing work. In mechanics a body is capable of doing work under two circumstances: (i) when it has motion and (ii) when it is situated in a field or when it is strained. When a bullet strikes a target it penetrates through the target and work is done against the resisting force offered by the target.
This energy is called kinetic energy of the body and is measured by the work it can do in being brought to rest.
Definition of kinetic energy:The capacity of doing work by virtue of motion is called kinetic energy and is measured by the total work that the body particle can do before coming to rest.
When a body is placed in a field, it can do work due to its position in the field. Such energy is called potential energy and is equal to the work done by an agent in placing it in the present position after bringing it from a position of zero field i.e., from infinity.
Due to position in earth’s gravitational field a body possesses energy called gravitational potential energy. Similarly, we have magnetic potential energy, electric potential energy. A compressed spring is capable of doing work due to strain produced in it. This is called elastic potential energy. The unit of energy is obviously the same as work.
Definition of potential energy:The capacity of doing work by virtue of position in a field or configuration is called potential energy and is measured by the work done by an agent in placing it in the present position after bringing it from infinity or the work done by the agent in producing the present configuration.
Units of Energy: The basic unit of energy is ‘joule’. In atomic and nuclear physics this is a too big unit. Here the convenient unit is ‘electron-volt’ (eV). This is defined as the energy gained by an electron when it falls through a potential difference of 1 volt. 1 eV = 1.6 × 10–19 J.
1 million electron volt (1 MeV) = 106 eV = 1.6 × 10–13 joule.
When energy to be expressed is very large, joule is found inconvenient. There we use bigger units, viz. watt-hour and kilowatt-hour.
1 watt-hour = 3600 joule and 1 killowatt-hour (kWH) = 3600 × 1000 joule = 3.6 megajoule (MJ).
Kinetic Energy and the Work-Energy theorem
Let a particle of mass m move with velocity v. To calculate its kinetic energy we have to see what amount work it can do in being brought to rest by an external opposing force. Let F be a constant opposing force applied on the particle and let it be brought to rest within s.
from third equation vf2– vi2= 2as where a = retardation produced by F, Put vf= 0 , vi = v
we get \displaystyle s=\frac{{{{v}^{2}}}}{{2a}}
Now KEf– KEi = Work done = F.s.cos(180) ( but KEf = 0 and let KEi = K)
-K = – ma\times \frac{{{{v}^{2}}}}{{2a}} (QF = ma)
K= \frac{1}{2}m{{v}^{2}}.
Kinetic energy (K) of a particle of mass having velocity v=\frac{1}{2}m{{v}^{2}}.
In terms of momentum, K=\frac{{{{p}^{2}}}}{{2m}} (Qp = mv)
Now we will show that the change in the kinetic energy of a particle is always equal to the work done on the particle by the force whether the force is constant or variable.
We have in general,
W=\int_{{{{x}_{1}}}}^{{{{x}_{2}}}}{{Fdx=}}\int_{{{{x}_{1}}}}^{{{{x}_{2}}}}{{m\frac{{dv}}{{dt}}}}\ dx
\left( {\because \ \ \ \ \ \ F=m\frac{{dv}}{{dt}}\text{ by Newton }\!\!’\!\!\text{ s law}} \right)
or W=\int_{{{{x}_{1}}}}^{{{{x}_{2}}}}{{m\frac{{dv}}{{dx}}.\frac{{dx}}{{dt}}}}\,dx
or W=m\int_{{{{x}_{1}}}}^{{{{x}_{2}}}}{{\frac{{dv}}{{dx}}.v}}\,dx
\left( {\because \ \ \ \ \ v=\frac{{dx}}{{dt}}} \right)
=\int_{{{{v}_{1}}}}^{{{{v}_{2}}}}{{mv\ dv}}=\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}
or W = K2 – K1 = ΔK.
Thus the work done on a particle by a force (constant or variable) is always equal to the change in the kinetic energy of the particle. This is known as the work-energy theorem.
Illustration
A block weighing 5 kg slides on a horizontal frictionless table with a speed of 1.2 ms–1. It is brought to rest in compressing a spring in its path. By how much is the spring compressed if its force constant is 3.5 Newton per metre?
Solution
By the ‘work energy’ theorem, Work done = change in kinetic energy.
Here work done =\frac{1}{2}k{{x}^{2}}
\frac{1}{2}k{{x}^{2}}=\frac{1}{2}m{{v}^{2}}, or x=\sqrt{{\frac{m}{k}}}.\ v=\sqrt{{\frac{5}{{3.5}}}}.1.2
or, x = 1.43 metre. Ans.
Potential Energy
Potential energy is energy due to position. If a body is in a position such that if it were released it would begin to move, it has potential energy.
There are two common forms of potential energy, gravitational and elastic.
(a) Gravitational Potential Energy, it is a property of height.
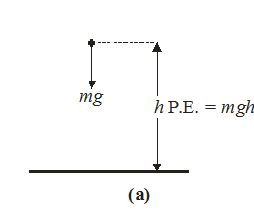
When an object is allowed to fall from one level to a lower level it gains speed due to gravitational pull, i.e., it gains kinetic energy. Therefore, in possessing height, a body has the ability to convert its height into kinetic energy, i.e., it possessed potential energy.
The magnitude of its gravitational potential energy is equivalent to the amount of work done by the weight of the body in causing the descent.
If a mass m is at a height h above a lower level the P.E. possessed by the mass is (mg) (h).
Since h is the height of an object above a specified level, an object below the specified level has negative potential energy.
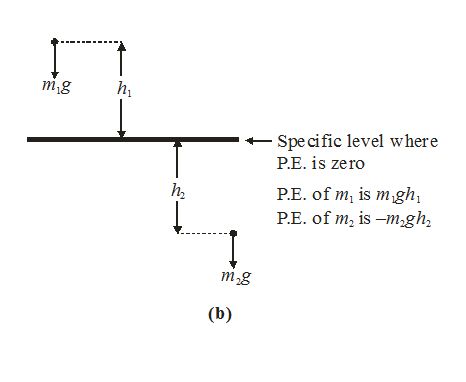
Therefore PE=+mgh
Important
The chosen level from which height is measured has no absolute position. It is important therefore to indicate clearly the zero P.E. level in any problem in which P.E. is to be calculated.
(b) Elastic Potential Energy, it is a property of stretched or compressed springs.
The end of a stretched elastic spring will begin to move if it is released. The spring therefore possesses potential energy due to its elasticity. (i.e., due to change in its configuration)
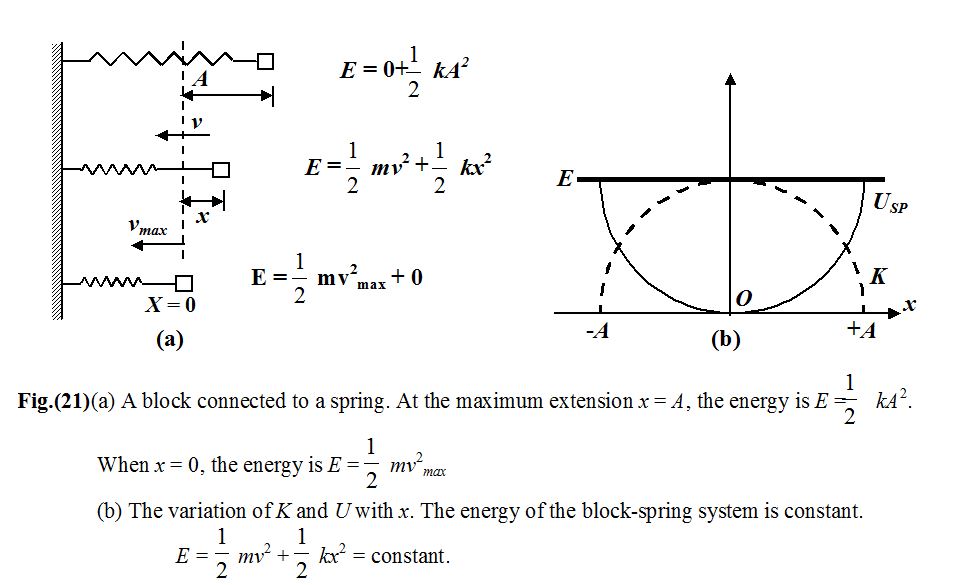
The amount of elastic potential energy stored in a spring of natural length a and spring constant k when it is extending by a length x is equivalent to the amount of work necessary to produce the extension.
we will see later that this work done will be \frac{1}{2}k{{x}^{2}} so \text{E}\text{.P}\text{.E}\text{.}=\frac{1}{2}k{{x}^{2}}
Important
E.P.E. is never negative whether due to extension or to compression.
CONSERVATION OF MECHANICAL ENERGY
From the previous section we know that the work done by a conservative force in terms of the change in potential energy is given by
ΔU = –WC …(5)
where U is the potential energy and WCis the work done by a conservative force.
From the work-energy theorem, we know that
Wnet= ΔK
Where Wnetrepresents the sum of work done by all the forces acting on the mass.
If a particle is subject to only conservative forces, then
WC= Wnet= ΔK
Thus, the equation (5) becomes,
ΔU = -ΔK
or ΔU + ΔK = 0 …(6)
The equation (5) tells us that the total change in potential energy plus the total change in kinetic energy is zero if only conservative forces are acting on the system.
That is, there is no change in the sum of K plus U.
Δ(K + U) = 0 …(7)
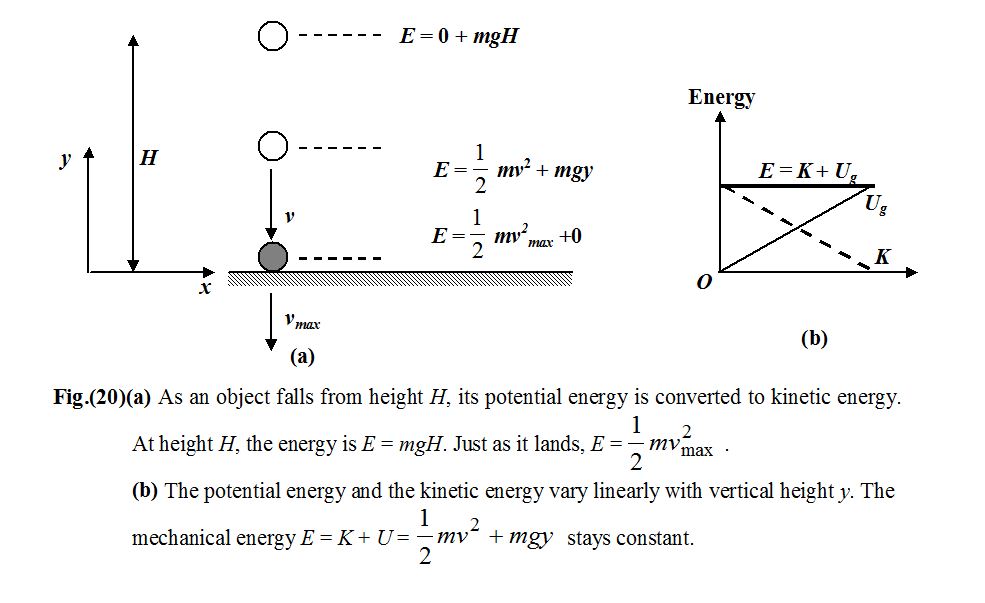
or ΔE = 0 where E = K + U
The quantity E = K + U is called the total mechanical energy.
According to equation (7), when only conservative forces act, the change in total mechanical energy of a system is zero, in otherwords,
If only conservative forces perform work on and within a system of masses, the total mechanical energy of the system is conserved.
Alternatively, the equation (7) may be written as
(Kf+ Uf) – (Ki+ Ui) = 0
or Kf+ Uf= Ki+ Ui
Since ΔE = 0, integrating both sides,
we get E = constant.
Illustration
A 1 kg block collides with a horizontal weightless spring of k = 2 Nm–1. The block compresses the spring 4m from the initial position. The coefficient of friction is 0.25. What was the speed of the block at the instant of collision?
Solution
Work done by the frictional force = –μmgx
(minus because displacement takes place opposite to the direction of force)
= –0.25 × 1 × g × 4 = –9.8 J.
Work done by the elastic force = -\frac{1}{2}k{{x}^{2}} = -\frac{1}{2}\times 2\times {{4}^{2}}=-16\text{J}.
Change in kinetic energy = \frac{1}{2}m({{v}^{2}}-v_{0}^{2}) = \frac{1}{2}\times 1\times ({{0}^{2}}-v_{0}^{2})=-\frac{{v_{0}^{2}}}{2}.
By the ‘work-energy’ theorem,
-\frac{{v_{0}^{2}}}{2}=-16-9.8,or v_{0}^{2}=2\times 25.8
or,
{{v}_{0}}=\sqrt{{51.6}}\ =7.2\text{m}{{\text{s}}^{{-\text{1}}}}.Ans.
Illustration
A small block of mass 100 g is pressed against a horizontal spring fixed at one end and compression is 5 cm. The spring constant is 100 N/m. When the block moves horizontally it leaves the spring. Where will it hit the ground 2 m below the spring?
(1) Horizontal distance of 1 m from end of spring.
(2) Horizontal distance of 2 m from end of spring.
(3) 0.5 m from free end of spring.
(4) 1.5 m from free end of spring.
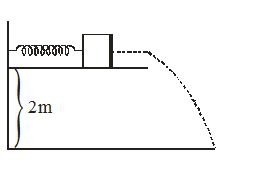
Solution
Let v be the velocity when it leaves the spring.
Then \frac{1}{2}m{{v}^{2}}=\frac{1}{2}k{{x}^{2}}
{{v}^{2}}=\frac{{k{{x}^{2}}}}{m}=\frac{{100\times {{{(0.05)}}^{2}}}}{{100\times {{{10}}^{{-3}}}}}
v=10\times 0.05\sqrt{{10}}m/ second
Time to fall vertical distance of 2 metre from the spring
=\sqrt{{\frac{{2s}}{g}}}=\sqrt{{\frac{{2\times 2}}{{10}}}}=\frac{2}{{\sqrt{{10}}}}
Horizontal distance =\frac{2}{{\sqrt{{10}}}}\times v=\frac{2}{{\sqrt{{10}}}}\times 10\times 0.05\times \sqrt{{10}}=1\text{m}.
∴ Option (1) Is The Correct Answer.
Practice Questions (Level-1)
1.
The temperature at the bottom of a high waterfall is higher than that at the top because
(a) by itself heat flows from higher to lower temperature
(b) the difference in height causes a difference in pressure
(c) thermal energy is transformed into mechanical energy
(d) mechanical energy is transformed into thermal energy
Ans (d)
2.
A bead X resting on a smooth horizontal surface, is connected to two identical springs and is made to oscillate to and fro along the line of the spring. When the bead passes through the central position, its energy is
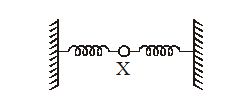
(a) zero
(b) mostly potential energy
(c) all potential energy
(d) all kinetic energy
Ans (d)
3.
The work done in stretching a spring of force constant k from length l1 to 12 is
(a) k(l_{2}^{2}-l_{1}^{2})
(b) \frac{1}{2}k(l_{2}^{2}-l_{1}^{2})
(c) k({{l}_{2}}-{{l}_{1}})
(d) k/2({{l}_{2}}+{{l}_{1}})
Ans (b)
4.
Figure shows force-distance graph of a particle moving along a straight line due north. The kinetic energy of the particle at a distance of 3 m from the starting point is
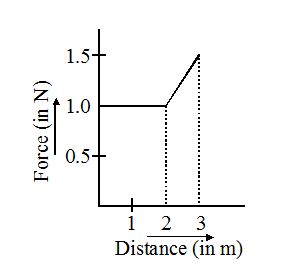
(a) 3.25 J
(b) 5.75 J
(c) 8.0 J
(d) 9.0 J
Ans (a)
5.
If the force acting on a body is inversely proportional to its velocity, then the kinetic energy acquired by the body in time ‘t’ is proportional to
(a) t0
(b) t1
(c) t2
(d) t4
Ans (d)
6.
If two electrons are forced to come closer to each other, then the potential energy of the electrons
(a) become zero
(b) increase
(c) decrease
(d) become infinite
Ans (d)
7.
Two springs A and B (kA = 2 kB) are stretched by applying forces of equal magnitude at the free ends. If the energy stored in A is E, that in B is
(a) E/2
(b) 2E
(c) E
(d) E/4
Ans (b)
8.
A body of mass 2 kg slides down a curved track which is quadrant of a circle of radius 1m. All the surface are frictionless. If the body starts from rest, its speed at the bottom of the track is
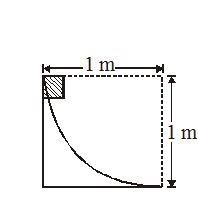
(a) 4.43 ms–1
(b) 2 ms–1
(c) 0.5 ms–1
(d) 19.6 ms–1
Ans (a)
Q.9
A car accelerates from rest to a speed of 10 m/s. Let energy spent be E. If we accelerate the car from 10 m/s to 20 m/s, the energy spent will be
(a) E (b) 2 E (c) 3 E (d) 4E
Ans. (c)
Q.10
There is a hemispherical bowl of radius R. A block of mass m slides without friction from the rim of the bowl to the bottom. The velocity of the block at the bottom will be
(a) \sqrt{{Rg}}
(b) \sqrt{{2Rg}}
(c) \sqrt{{2\pi Rg}}
(d) \sqrt{{\pi Rg}}
Ans. (b)
Q.11
The total work done on a particle is equal to the change in its kinetic energy
(a) always
(b) only if the forces acting on the body are conservative
(c) only if the forces acting on the body are gravitational
(d) only if the forces acting on the body are elastic
Ans. (a)
Q.12
A person pulls a bucket of water from a well of depth h. If the mass of uniform rope is m and that of the bucket full of water M, the work done by the person is
(a) \left( {M+\frac{m}{2}} \right)gh
(b) \frac{1}{2}\left( {M+m} \right)gh
(c) \left( {M+m} \right)gh
(d) \left( {\frac{M}{2}+m} \right)gh
Ans. (a)
Q.13
A mass of 2 kg falls from a height of 40 cm on a spring of force constant 1960 N/m. The spring is compressed by
(a) 10 cm (b) 0.4 cm (c) 0.01 cm (d) 0.04 cm
Ans. (a)
Q.14
In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle q with the vertical.
(a) q = cos-1(1/3)
(b) q = 60o
(c) q = cos-1(2/3)
(d) q = 0
Ans. (a)
Q.15
Which of the following can be negative
(a) Kinetic energy
(b) Potential energy
(c) Mechanical energy
(d) b & c both
Ans. (d)
Practice Questions (Level-2)
1.
A stone is falling freely in free space. Its velocity is x when it has lost y units of potential energy in the gravitational field of earth. Then the mass of the stone is
(a) xy
(b) \frac{{2y}}{{{{x}^{2}}}}
(c) x + y
(d) \frac{{2y}}{x}+9.8
Ans (b)
2.
A 20 Newton stone falls accidentally from a height of 4 m on to a spring of spring constant 1960 Nm–1. The maximum distance to which the spring shall suffer compression is
(a) \frac{2}{7}\text{m}
(b) \frac{3}{7}\text{m}
(c) \frac{4}{6}\text{m}
(d) 0.3295 m
Ans (a)
3.
A block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface. The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 m above the horizontal surface, then it would move a distance S on the rough surface. The value of S is [g = 10 ms–2]

(a) 1m
(b) 2m
(c) 3m
(d) 5m
Ans (d)
4.
The work done by the all-external forces on a system equals the change in
(a) total energy
(b) kinetic energy
(c) potential energy
(d) none of these
Ans (a)
5.
A block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. The speed of the block as it passes through the mean position shown is
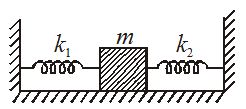
(a) \sqrt{{\frac{{{{k}_{1}}}}{m}}}\ x
(b) \sqrt{{\frac{{{{k}_{2}}}}{m}}}\ x
(c) \sqrt{{\frac{{{{k}_{1}}+{{k}_{2}}}}{m}}}\ x
(d) \sqrt{{\frac{{{{k}_{1}}-{{k}_{2}}}}{m}}}\ x
Ans (c)
6.
A small body of mass m slides down from the top A of a smooth hill of height H with initial velocity zero. The hill becomes horizontal at the edge B whose height is h from the ground. Assume that the body falls at maximum distance away from the foot of the hill. Then the value of h is
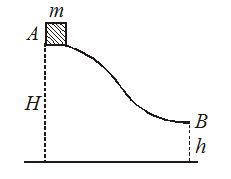
(a) H
(b) \frac{H}{2}
(c) \frac{H}{3}
(d) \frac{H}{4}
Ans (b)
7.
An unloaded bus can be stopped by applying brakes on straight road after covering a distance x. Suppose the passengers add 50% of its weight as the load and the braking force remains unchanged. How long will the bus go after the application of the brakes? [The velocity of the bus is same in both the cases]
(a) x
(b) 1.5 x
(c) 2 x
(d) 2.5 x
Ans (b)
8.
Consider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, the maximum elongation of the spring is
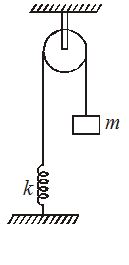
(a) \frac{{mg}}{k}
(b) \frac{{2mg}}{k}
(c) \frac{{3mg}}{k}
(d) \frac{{4mg}}{k}
Ans (b)
9.
A body of mass 1kg accelerates uniformly from rest to a velocity of 1 ms–1 in 15 second. The kinetic energy of the body will be \frac{2}{9}Jwhen ‘t’ is equal
(a) 4 s
(b) 8 s
(c) 10 s
(d) 12 s
Ans (c)
10.
A weight W suspended from a spring is raised through a height h so that the spring becomes just slack. If E was the energy of the stretched spring, then the gain in gravitational potential energy is
(a) Wh
(b) Wh + E
(c) Wh – E
(d) E
Ans (b)
11.
The pointer reading vs load graph from a spring balance is given in the figure. The spring constant is
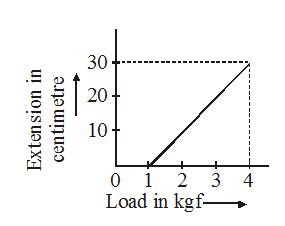
(a) 0.1 kgf/cm
(b) 5 kgf/cm
(c) 0.3 kgf/cm
(d) 1 kgf/cm
Ans (a)
12.
The velocity of the bob of an oscillating simple pendulum of length 1 m is 2ms–1 at the lowest position. When the bob is at the extreme position, the angle made by the string of the pendulum with the vertical is [g = 10 ms–2]
(a) cos–1 (0.4)
(b) cos–1 (0.6)
(c) cos–1 (0.8)
(d) 30°
Ans (c)
13.
A pendulum bob has been pulled aside from its equilibrium position through an angle a and then released. If l is the length of the pendulum, then the bob will reach the equilibrium position with speed of
(a) \sqrt{{2gl}}
(b) \sqrt{{2gl\cos \alpha }}
(c) \sqrt{{2gl(1-\cos \alpha )}}
(d) \sqrt{{2gl(1-\sin \alpha )}}
Ans (c)
14.
A spring with a force constant K obeys Hooke’s Law. It requires 4J of work to stretch it through 10 cm beyond its unstretched length. Calculate K and the extra work required to stretch it through additional 10 cm.
(a) 800 N/m; 5J
(b) 800 N/m; 7J
(c) 800 N/m; 12J
(d) 800 N/m; 10J
Ans (c)
15.
A running man has half the kinetic energy of a boy whose mass is half the mass of the man. The man speeds up by 1ms–1 and then has the same kinetic energy as the boy. What were the original speeds of mass and boy?
(a) 2.41 ms–1, 4.828 ms–1
(b) 2.41 ms–1, 3.004 ms–1
(c) 2.41 ms–1, 4.503 ms–1
(d) 2.41 ms–1, 5.664 ms–1
Ans (a)
Q.16
A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement ‘x’ is proportional to
(a) x (b) x2 (c) ln x (d) ex
Ans. (b)
Q.17
It requires twenty turns of the stem of a watch to wind the main spring and this stored sufficient energy to keep the watch running for 30.0 hours. If ten turns are given to the stem, it will run for
(a) 20 hrs (b) 15 hrs (c) 7.5 hrs (d) 3.75 hrs
Ans. (c)
Q.18
A chain is held on a frictionless table with one third of its length hanging over the edge. If the chain has a length L and mass M, how much work is required to pull the hanging part back on the table
(a) mgL
(b) \frac{{MgL}}{3}
(c) \frac{{MgL}}{9}
(d) \frac{{MgL}}{{18}}
Ans. (d)
Q.19
A particle falls from rest under gravity. Its potential energy with respect to ground (PE) and its kinetic energy (KE) are plotted against time (t). Choose the correct graph
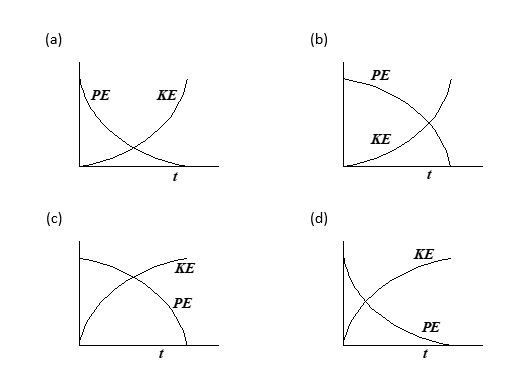
Ans. (c)
Q.20
For the system shown in the figure, initially the spring is compressed by a distance a from its natural length and when released, it moves to a distance b from its equilibrium position. The decrease in amplitude for one half-cycle (-a to b ) is
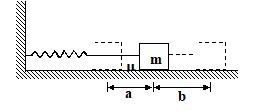
(a) \frac{{\mu mg}}{K}
(b) \frac{{2\mu mg}}{K}
(c) \frac{{\mu g}}{K}
(d) \frac{K}{{\mu mg}}
Ans. (b)
Q.21
Two identical cylindrical vessels with their bases at the same level, each contains a liquid of density r. The height of the liquid in one vessel is h1 and that in the other is h2. The area of either base is A. The work done by gravity in equalizing the levels when the vessels are interconnected is
(a) A\rho g\left( {\frac{{{{h}_{1}}-{{h}_{2}}}}{2}} \right)
(b) A\rho g{{\left( {\frac{{{{h}_{1}}-{{h}_{2}}}}{2}} \right)}^{2}}
(c) A\rho g\left( {\frac{{{{h}_{1}}-{{h}_{2}}}}{4}} \right)
(d) A\rho g{{\left( {\frac{{{{h}_{1}}-{{h}_{2}}}}{4}} \right)}^{2}}
Ans. (b)
Q.22
If the kinetic energy of a body is increased by 300%, its momentum will increase by
(a) 100% (b) 150% (c) 200% (d) 400%
Ans. (a)
Q.23
The force acting on a particle of mass 1 kg, starting from rest from the origin, is shown in the figure. The velocity of the particle at x = 2 m is
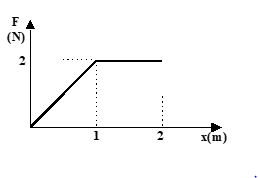
(a) 2\sqrt{2} m/s
(b) \sqrt{6} m/s
(c) m/s
d) \sqrt{3} m/s
Ans. (b)
Comprehension ( Q- 24 to Q-26 )
A spring lies along an x axis attached to a wall at one end and a block at the other end. The block rests on a frictionless surface at x = 0. A force of constant magnitude F is applied to the block that begins to compress the spring, until the block comes to a maximum displacement xmax.
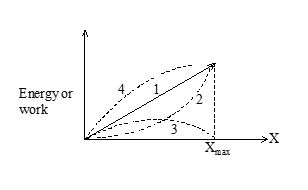
Questions:
Q.24
During the displacement, which of the curves shown in the graph best represents the kinetic energy of the block.
(a) 1 (b) 2 (c) 3 (d) 4
Ans. (c)
Q.25
During the displacement, which of the curves shown in the graph best represents the work done on the spring block system by the applied force.
(a) 1 (b) 2 (c) 3 (d) 4
Ans. (a)
Q.26
During the first half of the motion, applied force transfers more energy to the
(a) kinetic energy
(b) potential energy
(c) equal to both
(d) depends upon mass of the block
Ans. (a)

