Video Lecture
Theory For Notes Making
Rate of Flow
The rate of flow of a liquid is expressed in terms of its volume that flows out from an orifice of known cross-sectional area in unit time. All liquids are practically incompressible and the rate of flow through any section is the same. The rate of flow of a liquid hence is defined as the volume of it that flows across any section in unit time. For example, if the velocity of flow of a liquid is v in a direction perpendicular to two sections A and B of area A and distant l apart and if t be the time taken by the liquid to flow from A to B, we have vt = l. Obviously the volume of liquid flowing through section AB is equal to cylindrical column AB = lA or vtA.
Rate of flow of liquid = \frac{{vtA}}{t} = vA
Sometimes the rate of flow of liquid is expressed in terms of mass of liquid flowing across any section in unit time vA \displaystyle \rho where \displaystyle \rho is the density of liquid.
Streamlines
In steady flow the velocity v at a given point does not change with time. Consider the path ABC of a fluid particle in a steady flow and let the velocities be \displaystyle {{\overrightarrow{V}}_{1}}, \displaystyle {{\overrightarrow{V}}_{2}} , \displaystyle {{\overrightarrow{V}}_{3}} at A, B and C respectively as shown in the figures..
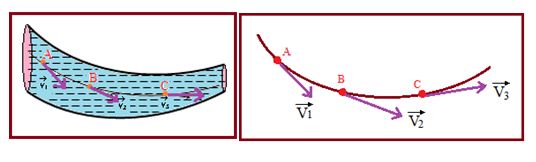
Because \displaystyle {{\overrightarrow{V}}_{1}} does not change with time any particle passing through A will have the same velocity \displaystyle {{\overrightarrow{V}}_{1}} and follow the same path ABC. This curve is called a streamline. A streamline is parallel to the velocity of fluid particle at every point. No two streamlines will ever cross each other. Otherwise any particle at the point of intersection will have two paths to go so that the flow will no more be steady. In non-steady flows the pattern of streamline changes with time. In steady flow if we draw a family of streamlines the tangent to the streamline at any point gives the direction of instantaneous velocity of the fluid at that path of motion. Thus as long as the velocity pattern does not change with time, the streamlines are also the paths along which the particles of the fluid move. In this type of flow the fluid between two surfaces formed by sets of adjacent streamlines is confined to the region between these two surfaces. This is so since the velocity vector has no component perpendicular to any streamline. The flow may be considered to occur in sheets or layers. Hence it is also sometimes called laminar flow. This type of flow is possible only if the velocity is below a certain limiting value called critical velocity. Above this velocity the motion is said to be unsteady or turbulent. The streamlines may be straight or curved depending on to the lateral pressure as it is the same throughout or different.
Tube of Flow
In a fluid in steady flow, if we select a finite number of streamlines to form a bundle like the streamline pattern shown in figure below the tubular region is called a tube of flow.
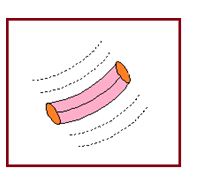
The tube of flow is bounded by streamlines so that no fluid can flow across the boundaries of the tube of flow and any fluid that enters at one end must leave at the other end.
Turbulent flow : When a liquid moves with a velocity greater than its critical velocity, the motion of the particles of liquid becomes disordered or irregular. Such a flow is called a turbulent flow.
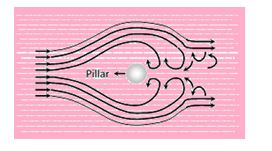
In a turbulent flow, the path and the velocity of the particles of the liquid change continuously and haphazardly with time from point to point. In a turbulent flow, most of the external energy maintaining the flow is spent in producing eddies in the liquid and only a small fraction of energy is available for forward flow. For example, eddies are seen by the sides of the pillars of a river bridge.
Critical Velocity and Reynold’s Number
The critical velocity is that velocity of liquid flow upto which its flow is streamlined and above which its flow becomes turbulent.
Reynold’s number is a pure number which determines the nature of flow of liquid through a pipe.
It is defined as the ratio of the inertial force per unit area to the viscous force per unit area for a flowing fluid.
{{N}_{R}}=\frac{{\text{Inertial force per unit area}}}{{\text{Viscous }\,\text{force per unit area}}}
If a liquid of density \rho is flowing through a tube of radius r and cross section A then mass of liquid flowing through the tube per second \frac{{dm}}{{dt}}= volume flowing per second × density = Av\times \rho
Inertial force per unit area = P+\rho gh+\frac{1}{2}\rho {{v}^{2}}= = \frac{1}{2}\rho {{v}^{2}} = {{v}^{2}}\rho
Viscous force per unit area F/A=\frac{{\eta v}}{r}
So by the definition of Reynolds number
{{N}_{R}}=\frac{{\text{Inertial force per unit area}}}{{\text{Viscous force per unit area}}} =\frac{{{{v}^{2}}\rho }}{{\eta v/r}}=\frac{{v\rho r}}{\eta }
If the value of Reynold’s number
(i)
Lies between 0 to 2000, the flow of liquid is streamline or laminar.
(ii)
Lies between 2000 to 3000, the flow of liquid is unstable and changing from streamline to turbulent flow.
(iii)
Above 3000, the flow of liquid is definitely turbulent.
Equation of Continuity
Consider a thin tube of flow as in the figure. Let A1 and A2 be the area of cross-section of the tube perpendicular to the streamlines at P and Q respectively. If v1 is the velocity of fluid particle at P and v2 the velocity at Q, then the mass of liquid entering A1 in a small interval of time \displaystyle \Delta t is given by \displaystyle \Delta m1 = \displaystyle \rho 1A1v1 \displaystyle \Delta t.
The mass flux i.e., the mass of fluid flowing per unit time is \frac{{\Delta {{m}_{1}}}}{{\Delta t}}\ =\ {{\rho }_{1}}{{A}_{1}}{{v}_{1}}
Let \displaystyle \Delta t” 0 so that v and A does not vary appreciably. The mass flux at P is given by \displaystyle \rho 1A1v1. Similarly the mass flux at
Q = \displaystyle \rho 2A2v2 where \displaystyle \rho 1and \displaystyle \rho 2 are the densities of the fluid at P and Q respectively. Since no fluid crosses the wall of the tube of flow, the mass of fluid crossing each cross-section of the tube per unit time must be the same
\displaystyle \rho 1A1v1 = \displaystyle \rho 2A2v2
or \displaystyle \rho Av = constant
This equation expresses the law of conservation of mass in fluid dynamics and is called the Equation of Continuity. If the fluid is incompressible as in most liquids \displaystyle \rho = constant
A1v1 = A2v2 or Av = constant.
The product Av represents the rate of flow of fluid. Hence, v is inversely proportional to the area of cross-section along a tube of flow. Therefore, widely spaced streamlines indicate regions of low speed and closely spaced streamlines indicate regions of high speed.

Bernoulli’s Equation
It is a fundamental equation in fluid mechanics and can be derived from the work-energy theorem. The theorem states that the work done by the resultant force acting on a system is equal to the change in kinetic energy of the system.
Consider a steady, irrotational, non-viscous, incompressible flow of a fluid through a pipe or tube of flow as shown in the figure. A portion of the fluid flowing through a section of pipe line from the position ABCD TO PQRS as shown in the figure.
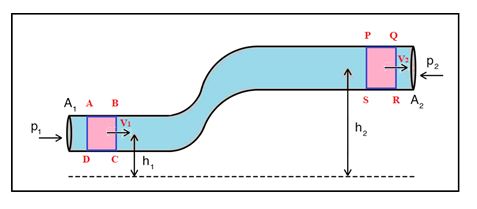
The pipeline is horizontal at A and P and are at heights h1 and h2 respectively from a reference plane. The pipeline gradually widens from left to right. Let P1, A1, v1 and P2, A2, v2 be the pressures, areas of cross-section and velocities at A and P respectively.
Suppose the fluid which escapes the volume ABCD = A1 \displaystyle \Delta l1 flows out at P after some time and occupies PQRS which is equal to A2 \displaystyle \Delta l2 as indicated in (a) and figure(b) respectively. The forces acting on the fluid are the pressure forces P1A1 and P2A2, the force of gravity at A and P. The work done on the system by the resultant force is as follows:
(i)
The work done on the system by pressure force P1A1 which is P1A1 \displaystyle \Delta l1
(ii)
The work done on the system by pressure force P2A2 that is –P2A2 \displaystyle \Delta l2, the negative sign implying that positive work is done by the system.
(iii)
The gravitational work done by the system in lifting the mass m inside from the height h1 to height h2is given by mg (h2–h1) or the work done on the system will be –mg(h2–h1)
Hence the work done by the resultant force on the system is the sum of all the above terms.
W = P1A1 \displaystyle \Delta l1–P2A2 \displaystyle \Delta l2–mg (h2–h1)
Since A1 \displaystyle \Delta l1 = A2 \displaystyle \Delta l2 we can put {{A}_{1}}\Delta {{l}_{1}}=\ {{A}_{2}}{{l}_{2}}\ =\ \frac{m}{\rho } where \displaystyle \rho is the density of the fluid
W = (P1–P2) \frac{m}{\rho }–mg (h2–h1)
The change in kinetic energy of the fluid is \Delta K\,=\,\frac{1}{2}\,mv_{2}^{2}-\frac{1}{2}\,mv_{1}^{2}
From the work-energy theorem we can put the work done on the system is equal to the change in kinetic energy of the system.
({{P}_{1}}-\ {{P}_{2}})\ \frac{m}{\rho }\,\,-\ \,\,mg({{h}_{2}}-\ {{h}_{1}})\ \,=\ \,\frac{1}{2}\ mv_{2}^{2}\ \,-\ \,\frac{1}{2}\ mv_{1}^{2}
On multiplying both sides of equation by \displaystyle \rho /m and rearranging we get
{{P}_{1}}\,+\,\ \frac{1}{2}\ \rho v_{1}^{2}\ \,+\,\ \rho g{{h}_{1}}=\ {{P}_{2}}+\,\ \frac{1}{2}\ \rho v_{2}^{2}\ +\ \rho g{{h}_{2}}
Since the subscripts 1 and 2 refer to any two locations on the pipeline, we can write in general
P\,\ +\,\ \frac{1}{2}\ \rho {{v}^{2}}+\ \rho gh= constant.
The above is called Bernoulli’s equation for steady non-viscous incompressible flow. Dividing the above equation by \displaystyle \rho g we can rewrite the above as
h\ +\ \frac{{{{v}^{2}}}}{{2g}}\ \,+\ \,\frac{P}{{\rho g}}= constant, which is called total head.
Out of the three components of the total head on the left hand side of the above equation the first term ‘h’ is called elevation head or gravitational head, the second term \frac{{‘{{v}^{2}}’}}{{2g}} is called velocity head and the third term \frac{{‘P’}}{{\rho g}} is called pressure head.
Now if the liquid flows horizontally its potential energy remains constant so that the Bernoulli’s equation becomes P\ \,+\ \,\frac{1}{2}\ \rho {{v}^{2}} = constant. Further if the fluid is at rest or v = 0, P + \displaystyle \rho gh = constant.
The pressure (P + \displaystyle \rho gh) which would be present also when there is flow is called the static pressure while the term \frac{1}{2}\ \rho {{v}^{2}} is called the dynamic pressure. The equation shows that for an ideal liquid the velocity increases when pressure decreases and vice-versa.
Applications of Bernoulli’s Theorem
We shall consider a few examples wherein Bernoulli’s principle is employed.
Filter pump:
In a filter pump water flows suddenly from a wide tube into a narrow one. The velocity is increased and pressure reduced far below the atmospheric pressure. The receiver to be exhausted is connected by a side tube with this region of low pressure. Air is carried along with water and in a short time air in the receiver is reduced to a pressure, which is slightly greater than the vapour pressure of water.
Atomizer or sprayer:
In flowing out of a narrow tube into the atmosphere or a wider tube, air produces a suction effect. In a sprayer a strong jet of air on issuing from a nozzle of a tube lowers the pressure over another tube, which dips in a liquid. The liquid is sucked up and mixed with air stream and thus a fine mist is produced.
Pitot tube:
This device is used to measure the flow speed of liquids and gases in pipes. It consists of a manometer tube connected into pipeline as shown in figure. One of the ends of the manometer tube A is connected with its plane of aperture parallel to the direction of flow of fluid while the other end B is perpendicular to it.
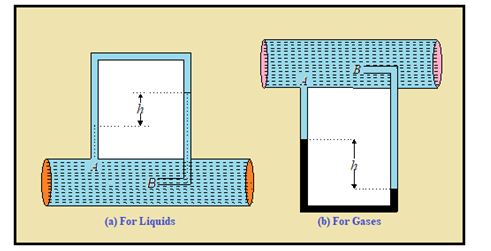
The pressure and velocity on the left arm of the manometer opening A remains the same as they are elsewhere and is equal to static pressure Pa. Since the velocity of fluid at B is reduced to zero the pressure is the full arm pressure. Applying Bernoulli’s principle, {{P}_{a}}+\,\ \frac{1}{2}\ \rho {{v}^{2}}=\ {{P}_{b}}which shows Pb>Pa. If h is the difference in height of liquid in the manometer and \displaystyle \rho ¢ the density of manometric liquid,
Pa + \displaystyle \rho ‘gh = Pb
\frac{1}{2}\ \rho {{v}^{2}}=\ {\rho }’gh
In case of Pitot tube \displaystyle \rho = \displaystyle \rho ¢
v2 = 2gh
In case of gas Pitot tube v\ =\ \sqrt{{\frac{{2gh{\rho }’}}{\rho }}}
Venturimeter:
This is a device based on Bernoulli’s principle used for measuring the flow of a liquid in pipes. A liquid of density \displaystyle \rho flows through a pipe of cross sectional area A. At the constricted part the cross sectional area is a. A manometer tube with a liquid say mercury having a density \displaystyle \rho ‘ is attached to the tube as shown in figure.
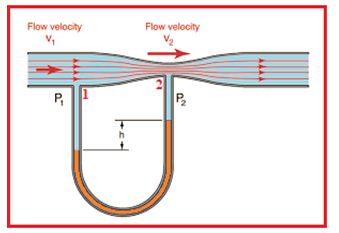
If P1 is the pressure at point 1 and P2 the pressure at point 2 we have
\frac{{{{P}_{1}}}}{\rho }\,\ +\,\ \frac{1}{2}v_{1}^{2}\,\ =\,\ \frac{{{{P}_{2}}}}{\rho }\,\ +\ \,\frac{1}{2}v_{2}^{2} where v1 and v2 are the velocities at these points respectively.
We have Av1 = av2
{{v}_{1}}=\,\ \frac{{a{{v}_{2}}}}{A}
\frac{1}{2}v_{1}^{2}\ \,-\,\frac{1}{2}\ v_{2}^{2}\ \,=\ \,\frac{{{{P}_{2}}}}{\rho }\ -\ \frac{{{{P}_{1}}}}{\rho }
=\ \frac{{{{P}_{2}}-\ {{P}_{1}}}}{\rho }
v_{1}^{2}\ -\ \frac{{{{A}^{2}}v_{1}^{2}}}{{{{a}^{2}}}}\ =\ \frac{{2({{P}_{2}}-{{P}_{1}})}}{\rho }’
v_{1}^{2}\ \left( {1\ -\ \frac{{{{A}^{2}}}}{{{{a}^{2}}}}} \right)\ \,=\ \,\frac{{2({{P}_{2}}-{{P}_{1}})}}{\rho }
v_{1}^{2}\ =\ \frac{{2({{P}_{2}}-\ {{P}_{1}})}}{{\left( {1\ -\ \frac{{{{A}^{2}}}}{{{{a}^{2}}}}} \right)\ \rho }}\ \,=\ \,\frac{{2{{a}^{2}}({{P}_{2}}-\ {{P}_{1}})}}{{({{a}^{2}}-\ {{A}^{2}})\ \rho }}
If a<A, v_{1}^{2}\,\ =\ \,\frac{{2{{a}^{2}}({{P}_{1}}-\ {{P}_{2}})}}{{({{A}^{2}}-\ {{a}^{2}})\ \rho }}, {{v}_{1}}=\ \sqrt{{\frac{{2({{P}_{1}}-\ {{P}_{2}})\ {{a}^{2}}}}{{({{A}^{2}}-\ {{a}^{2}})\ \rho }}}}
Volume of liquid flowing through the pipe per sec. = Av1 = Q
Q\ \,=\,\ Aa\ \sqrt{{\frac{{2({{P}_{1}}-\ {{P}_{2}})}}{{({{A}^{2}}-\ {{a}^{2}})\ \rho }}}}
Speed of Efflux
As shown in figure represents a tank of cross-sectional area A1, filled to a depth h with a liquid of density \displaystyle \rho . There is a hole of cross-sectional area A2 at the bottom and the liquid flows out of the tank through the hole A2<<A1
Let v1 and v2 be the speeds of the liquid at A1 and A2.
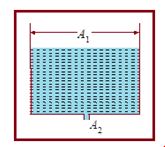
As both the cross-sections are open to the atmosphere, the pressures there equals the atmospheric pressure P0. If the height of the free surface above the hole is h,
Bernoulli’s equation gives {{P}_{0}}+\ \,\frac{1}{2}\ \rho v_{1}^{2}\ +\ \rho gh\ =\ {{P}_{0}}+\ \frac{1}{2}\ \rho v_{2}^{2}
By the equation of continuity, A2v1 = A2v2
{{P}_{0}}+\,\ \frac{1}{2}\ \rho \ {{\left[ {\frac{{{{A}_{2}}}}{{{{A}_{1}}}}} \right]}^{2}}v_{2}^{2}\ +\ \rho gh\,\ =\,\ {{P}_{0}}+\ \frac{1}{2}\rho v_{2}^{2}
\left[ {1\ -\ {{{\left( {\frac{{{{A}_{2}}}}{{{{A}_{1}}}}} \right)}}^{2}}} \right]\ v_{2}^{2}\ =\ 2ghÞv2 = \sqrt{{\frac{{2gh}}{{1-{{{\left( {\frac{{{{A}_{2}}}}{{{{A}_{1}}}}} \right)}}^{2}}}}}}
If A2<<<A1, the equation reduces to {{v}_{2}}=\ \sqrt{{2gh}}
The speed of efflux is the same as the speed a body would acquire in falling freely through a height h. This is known as Torricelli’s theorem.
Illustration
A tube having its two limbs bent at right angles to each other is held with one end dipping in a stream and opposite to the direction of the flow. If the speed of stream is 2.68 m/see, find the height to which the water rises in the vertical limb of the tube.
Solution:
Clearly the flow of water will be stopped by the tube dipping in the stream and facing the flow so that the loss of kinetic energy per unit mass of water is \frac{{{{v}^{2}}}}{2}. This will therefore be the gain in pressure energy i.e., \frac{P}{\rho }.
\frac{P}{\rho }\,\ =\ \,\frac{{{{v}^{2}}}}{2} or \ \ P\,\ =\ \,\frac{{{{v}^{2}}\rho }}{2}
If h is the height to which water rises in the tube P = h \displaystyle \rho g or h \displaystyle \rho g = \frac{{{{v}^{2}}\rho }}{2}
h = \ \frac{{{{v}^{2}}}}{{2g}}\ =\ \frac{{{{{(2.68)}}^{2}}}}{{2\ \times \ 9.8}} = 0.3664 metre or 36.64 cm
Illustration
If the diameters of a pipe are 10 cm and 6 cm at points where a venturimeter is connected and the pressures at these points are found to differ by 5 cm of water column, find the volume of water flowing through the pipe per second.
Solution:
We know A{{v}_{1}}=\ Aa\ \sqrt{{\frac{{2({{P}_{1}}-\ {{P}_{2}})}}{{({{A}^{2}}-\ {{a}^{2}})\ \rho }}}}
A\ =\ \pi r_{1}^{2}\ =\ \pi \ {{\left( {\frac{{10}}{2}} \right)}^{2}}=\ 25\ \pi \ c{{m}^{2}}= 25p´ 10–4 m2
a\ =\ \pi r_{2}^{2}\ =\ \pi \ {{\left( {\frac{6}{2}} \right)}^{2}}\ =\ 9\pi \ c{{m}^{2}}\ =\ 9\pi \ \times \ {{10}^{{-4}}}{{m}^{2}}
P1–P2 = 5 cm of water column = 5 x 10–2 x103 x 9.8 = 5 x 98 N/m2
Av1 = 25\pi \ \times \ 9\pi \ \times \ {{10}^{{-4}}}\sqrt{{\frac{{2\ \times \ 5\ \times \ 98\ \times \ {{{10}}^{{-3}}}}}{{{{{(25\pi )}}^{2}}\ -\ {{{(9\pi )}}^{2}}}}}}
= 225π 2 \sqrt{{\frac{{0.98}}{{34\pi \ \times \ 16\pi }}}}\ \times \ {{10}^{{-4}}}
= 30.00 x 10–4 m3/sec
= 3 litres/sec
Illustration
A Pitot tube is fixed in a main of diameter 15 cm and the difference in pressure indicated by gauge is 4 cm of water column. Find the volume of water passing through the main in one minute.
Solution:
Radius of main = 7.5 cm
Area of cross-section = π (7.5)2 cm2
Loss of kinetic energy = \frac{1}{2}\ {{v}^{2}}\ ergs
Gain of pressure energy = \frac{P}{\rho }\ =\ p\ =\ hg = 4 x 981 ergs
\frac{1}{2}{{v}^{2}} = 4 x 981
v = \sqrt{{7848}} = 88.59 cm/sec
Illustration
Water stands at a depth H in a tank whose side walls are vertical. A hole is made at one of the walls at a depth h below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor. What is the maximum possible range?
Solution:
Applying Bernoulli’s theorem at points A and B,
{{P}_{A}}+\ \frac{1}{2}\ \rho v_{A}^{2}\ +\ \rho g{{H}_{A}}=\ {{P}_{B}}+\ \frac{1}{2}\ \rho v_{B}^{2}\ +\ \rho g{{H}_{B}}
P\ +\ 0\ +\ \rho gH\ \,=\,\,\ P\ +\ \frac{1}{2}\ \rho {{v}^{2}}+\ \rho g(H\ -\ h)
v2 = 2gh
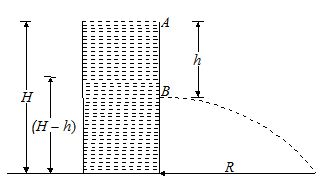
The vertical component of velocity of water emerging from hole B is zero. Therefore time taken (t) by the water to fall through a distance (H – h) is given by
H – h = \frac{1}{2}\ g{{t}^{2}}\ or\ t\ =\ \sqrt{{\frac{{2(H\ -\ h)}}{g}}}
Required horizontal range R = vt
= \sqrt{{2gh}}\ \sqrt{{\frac{{2(H\ -\ h)}}{g}}} = \text{2}\sqrt{{\text{h}\ \text{(H}\ -\ \text{h)}}}
The range R is maximum when \frac{{dR}}{{dh}} = 0 2\ \times \ \frac{1}{2}\ {{(Hh\ -\ {{h}^{2}})}^{{-\ \frac{1}{2}}}}(H\ -\ 2h)\ = 0
This gives h = \frac{H}{2}s
Maximum possible range = 2 \sqrt{{\frac{H}{2}\ \times \ \left( {H\ -\ \frac{H}{2}} \right)}} = H
VISCOSITY
If water in a tub is whirled and then left to itself, the motion of the water stops after some time. This is a very common observation. What stops the motion? There is no external force to stop it. A natural conclusion is, therefore, that whenever there is relative motion between parts of a fluid, internal forces are set up in the fluid, which oppose the relative motion between the parts in the same way as forces of friction operate when a block of wood is dragged along the ground. This is why to maintain relative motion between layers of a fluid an external force is needed as shown in the figure given below
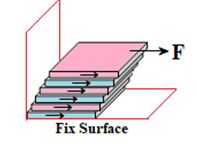
“This property of a fluid by virtue of which it oppose the relative motion between its different layers is known as viscosity and the force that is into play is called the viscous force”.
Consider the slow and steady flow of a fluid over a fixed horizontal surface. Let v be the velocity of a thin layer of the fluid at a distance x from the fixed solid surface.
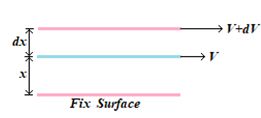
Then according to Newton, the viscous force acting tangentially to the layer is proportional to the area of the layer and the velocity gradient at the layer. If F is the viscous force on the layer, then
FµA where A is the area of the layer µ – \frac{{dv}}{{dx}}
The negative sign is put to account for the fact that the viscous force is opposite to the direction of motion.
F=-\eta A\frac{{dv}}{{dx}}
whereh is a constant depending upon the nature of the liquid and is called the coefficient of viscosity and Velocity gradient = \frac{{dv}}{{dx}}
If A = 1 and \frac{{dv}}{{dx}} = 1, we have F = -h
Thus the coefficient of viscosity of a liquid may be defined as the viscous force per unit area of the layer where velocity gradient is unity.
The coefficient of viscosity has the dimension [ML–1T–1] and its unit is Newton second per square metre (Nsm–2) or kilograme per metre per second (kgm–1s–1). In CGS the unit of viscosity is Poise
Remember these points regarding viscosity
(1)
Difference between viscosity and solid friction : Viscosity differs from the solid friction in the respect that the viscous force acting between two layers of the liquid depends upon the area of the layers, the relative velocity of two layers and distance between two layers, but the friction between two solid surfaces is independent of the area of surfaces in contact and the relative velocity between them.
(2)
From kinetic theory point of view viscosity represents transport of momentum, while diffusion and conduction represents transport of mass and energy respectively.
(3)
The viscosity of thick liquids like honey, glycerin, coaltaretc. is more than that of thin liquids like water.
(4)
The cause of viscosity in liquids is cohesive forces among molecules where as in gases, it is due to diffusion.
(5)
The viscosity of gases increases with increase of temperature, because on increasing temperature the rate of diffusion increases.
(6)
The viscosity of liquid decreases with increase of temperature, because the cohesive force between the liquid molecules decreases with increase of temperature
Relation between coefficient of viscosity and temperature; Andrade formula h = \frac{{A\,{{e}^{{C\rho /T}}}}}{{{{\rho }^{{-1/3}}}}}
Where T= Absolute temperature of liquid, \displaystyle \rho = density of liquid, A and C are constants.
Stoke’s Law
When a solid moves through a viscous medium, its motion is opposed by a viscous force depending on the velocity and shape and size of the body. The energy of the body is continually decreases in overcoming the viscous resistance of the medium. This is why cars, aeroplanes etc. are shaped streamline to minimize the viscous resistance on them.
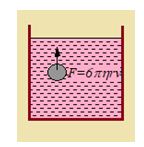
The viscous drag on a spherical body of radius r, moving with velocity v, in a viscous medium of viscosity h is given by
Fviscous= 6 \displaystyle \pi hrv.
This relation is called Stokes’ law
This law can be deduced by the method of dimensions. By experience we guess that the viscous force on a moving spherical body may depend on its velocity, radius and coefficient of viscosity of the medium. We may then write F = k varbhc
where k is a constant (dimensionless) and a, b and c are the constants to be determined.
By taking dimensions of both sides, we have MLT–2 = (LT–1)aLb(ML–1T–1)c
or, MLT–2 = McLa+b–cT–a–c
Equating powers of M, L and T we have c = 1
a + b–c = 1 and –a–c = -2
Solving we have a = 1, b = 1 and c = 1
F = khrv
Experimentally k is found to be 6 \displaystyle \pi ;
F = 6 \displaystyle \pi hrv.
Terminal Velocity
Let the body be driven by a constant force. In the beginning the viscous drag on the body is small. Velocity is small and so the body is accelerated through the medium by the driving force. With the increase of velocity of the body the viscous drag on it will also increase and eventually when it becomes equal to the driving force, the body will acquire a constant velocity. This velocity is called the terminal velocity of the body.
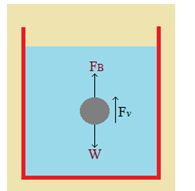
Consider the downward motion of a spherical body through a viscous medium such as a ball falling through liquid. If r is the radius of the body, \displaystyle \rho the density of the material of the body and s is the density of the liquid then,
the weight of the body W= \frac{{4\pi }}{3}{{r}^{3}}\rho g,downwards
and the buoyancy of the body FB = \frac{{4\pi }}{3}{{r}^{3}}\sigma g,upwards
The net downward driving force = \frac{{4\pi }}{3}{{r}^{3}}(\rho -\sigma )\,g
If v is the terminal velocity of the body, then the viscous force on the body is Fv = 6 \displaystyle \pi hrv
For no acceleration of the body we have
6 \displaystyle \pi hrv = \frac{{4\pi }}{3}{{r}^{3}}(\rho -\sigma )\,g or, v=\frac{2}{9}.\frac{{{{r}^{2}}g\,(\rho -\sigma )}}{\eta }
Illustration
Eight spherical drops of equal size fall vertically through air with a terminal velocity of 0.1 ms–1. What would be the velocity if these eight drops were to combine to form one large spherical drop?
Solution:
Let r1 be the radius of each small drop, and r2 that of the bigger drop. As the volume remains constant,
\frac{4}{3}\pi r_{2}^{3}=\frac{4}{3}\pi r_{1}^{3}\times 8 or, \frac{{{{r}_{1}}}}{{{{r}_{2}}}}=\frac{1}{2}
Since the terminal velocity is proportional to the square of the radius of the drop,
\frac{{{{v}_{1}}}}{{{{v}_{2}}}}={{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}^{2}}=\frac{1}{4}
v2 = 4 x 0.1 = 0.40 ms–1
Thus the terminal velocity of the bigger drop is 0.4 m/s.
Illustration
A gas bubble of diameter 2 cm rises steadily through a solution of density 1750 kgm–3 at the rate of 0.35 cm/s. Calculate the coefficient of viscosity of the solution.
Solution:
We have, v=\frac{2}{9}.\frac{{{{r}^{2}}g\ (\rho -\sigma )}}{\eta }
Here, \displaystyle \rho = density of air is negligible
v=-\frac{2}{9}.\frac{{{{r}^{2}}g\sigma }}{\eta }
The negative sign shows that the velocity is upward
\eta =\frac{2}{9}.\frac{{{{r}^{2}}g\sigma }}{v}=\frac{2}{9}.\frac{{{{{0.01}}^{2}}\times 9.8\times 1750}}{{0.0035}}
= 109 kgm–1 s–1 or Nsm–2
Illustration
A vertical tube of 4 mm diameter at the bottom has water passing through it. If the pressure be atmospheric at the bottom where the water emerges at the rate of 800 gm per minute, what is the pressure at a point in the tube 25 cm above the bottom where the diameter is 3 mm?
Solution:
Rate of emergence of water = 800 gm/minute = \frac{{40}}{3} gm/sec = \frac{{40}}{3} cm3/sec
Q density of water, \displaystyle \rho = 1 g/cm3
This will be the same across any section of the tube.
Diameter at bottom = 4 mm = 0.4 cm
Area of cross-section = \displaystyle \pi (0.2)2 = 0.04 \displaystyle \pi cm2
Volume of water passing through the bottom = cross-sectional area ´ velocity
Velocity of water passing through the bottom = \frac{{40}}{{3\ \,\times \,0.04\ \pi }} say (v1) cm/sec.
Kinetic energy per unit mass of water at the bottom = \frac{1}{2}\ v_{1}^{2}\ =\ \frac{1}{2}\ {{\left( {\frac{{40}}{{3\ \times \ 0.04\ \pi }}} \right)}^{2}} ergs
Pressure energy at the bottom = \frac{{{{P}_{1}}}}{\rho } = 76 x 13.6 x 981 ergs
Total energy = kinetic energy + pressure energy =\ \frac{1}{2}\ {{\left( {\frac{{40}}{{3\ \times \ 0.04\ \pi }}} \right)}^{2}} + (76 x 13.6 x 981)
Again diameter of tube above 25 cm = 3 mm = 0.3 cm
Area of cross-section = \displaystyle \pi (0.15)2 cm2
Velocity of flow of water = \frac{{40}}{{3\ \times \ \pi {{{(0.15)}}^{2}}}}
Kinetic energy per unit mass = \frac{1}{2}\ {{\left( {\frac{{40}}{{3\ \times \ \pi \ {{{(0.15)}}^{2}}}}} \right)}^{2}} ergs
Let the pressure be P2.
pressure energy per unit mass = P2 x 13.6 x 981
Also potential energy per unit mass of water = hg = 25 x 981 ergs
total energy = kinetic energy + pressure energy + potential energy
=\ \frac{1}{2}\ {{\left( {\frac{{40}}{{3\ \times \ \pi \ {{{(0.15)}}^{2}}}}} \right)}^{2}}+\ {{P}_{2}}(13.6\ \times \ 981)\ +\ (25\ \times \ 981)
Using Bernoulli’s theorem,
\frac{1}{2}\ {{\left( {\frac{{40}}{{3\ \times \ 0.04\pi }}} \right)}^{2}}+ (76 + 13.6 x 981) = \frac{1}{2}\ {{\left( {\frac{{40}}{{3\pi \ \times \ 0.0225}}} \right)}^{2}}+ (P2 x 13.6 x 981) + (25 x 981)
\frac{{800}}{{{{{(0.12\ \pi )}}^{2}}}}\ +\ (76\ \times \ 13.6\ \times \ 981)\ =\ \frac{{800}}{{{{{(0.0675\pi )}}^{2}}}}+ (P2 13.6 x 981) + (25 x 981)
5629 + 1013962 = 17790 + 13342P2 + 24525
13342P2 = 5629 + 1013962 – 17790 – 24525 = 977276
P2= 73.25 cm of Hg
Objective Assignment
Q.1
An incompressible non-viscous fluid flows steadily though a cylindrical pipe which has radius 2R at point A and radius R at point B farther along the flow direction. If the velocity at point A is V, its velocity at point B will be:
(a) 2V (b) V (c) V/2 (d) 4V
Ans. (d)
Q.2
Water is flowing through a pipe of uniform cross-section under constant pressure. At some place the pipe becomes narrow, the pressure of water at this place:
(a) increases
(b) decreases
(c) remains unchanged
(d) depends on several factors
Ans. (b)
Q.3
There is a hole at the bottom of a large open vessel. If water is filled up to a height h, its flow rate is v. If water is filled to a height 4h, its flow rate will be
(a) 4v (b) 3v (c) 2v (d) v
Ans. (c)
Q.4
A garden hose having an internal diameter 2.0 cm is connected to a lawn sprinkle that consists of an enclosure with 24 holes, each of 0.125 cm in diameter. If water in the hose has a speed of 90.0 cm/s, find the speed of the water having the sprinkler hole.
(a) 960 cm/s
(b) 256 cm/s
(c) 157 cm/s
(d) 595 cm/s
Ans (a)
Q.5
Water flows along the horizontal pipe of which the cross-section is not uniform. The pressure is 30 mm of Hg where the velocity is 0.20 m/s. Find the pressure at a point where the velocity is 1.20 m/s.
(a) 0.0075 m of Hg
(b) 0.165453 m of Hg
(c) 0.0864 m of Hg
(d) 0.02475 m of Hg
Ans (d)
Q.6
A small hole is made at a height of (1/ \sqrt{2}) m from the bottom of a cylindrical water tank and at a depth of h = \sqrt{2} m from the upper level of water in the tank. Find the distance, where the water emerging from the hole strikes the ground.
(a) 1 m
(b) 5 m
(c) 2 m
(d) 4 m
Ans (c)
Q.7
Air is streaming past a horizontal aeroplane wing such that its speed is 120 m/s over the upper surface and 90 m/s at the lower surface. If the density of air is 1.3 kg/m3, find the difference in pressure between the top and bottom of the wing. If the wing is 10 m long and has an average width 2 m, calculate the gross lift of the wing.
(a) 0.3 ´ 104 N
(b) 1.5 ´ 104 N
(c) 8.2 ´ 104 N
(d) 10.5 ´ 104 N
Ans (c)
Q.8
Three tubes A, B and C are connected to a horizontal pipe in which ideal liquid is flowing. The radii of the tubes A, B and C at the junction are respectively 2 cm, 1 cm and 2 cm. It can be said:
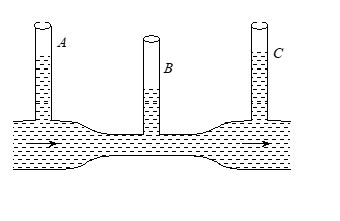
(a) The height of the liquid in the tube A is maximum
(b) Height of the liquid in the tubes A and B is same
(c) Height of the liquid in the tubes A, B and C is same
(d) Height of the liquid in the tubes A and C is same
Ans. (d)
Q.9
Water flows through a frictionless duct with a cross-section varying as shown in figure. Pressure p at point along the axis is represented by:
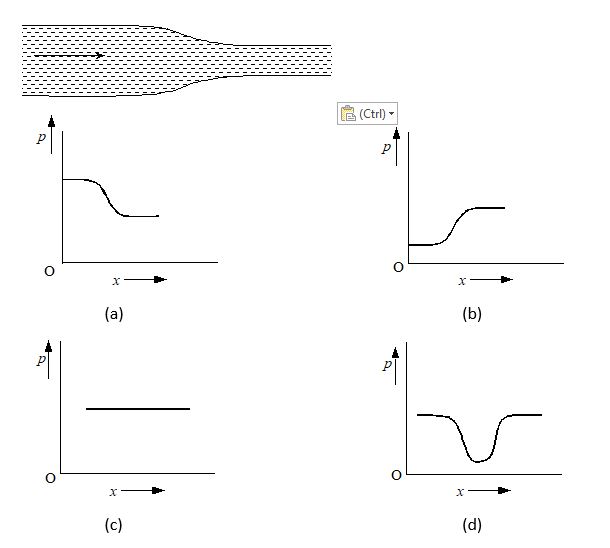
Ans. (a)
Q.10
Two drops of same radius are falling through air with steady velocity of v cm/s. If the two drops coalesce, what would be the terminal velocity?
(a) 4v (b) (4)1/3v (c) 2v (d) 64v
Ans. (b)
Q.11
When a tangential force of 0.02 N is applied on a large wooden plate of area 10 m2 floating on the surface of the river, plate moves with the speed 2 m/s on the river surface. IF the river is 1 m deep and the water in contact with the bed is stationary, then coefficient of viscosity of water is
(a) 2 ´ 10-2 poise
(b) 10-3 poise
(c) 10-4 poise
(d) 2 ´ 10-1 poise
Ans. (b)
Q.12
From amongst the following curves, which one shows the v ariation of the velocity v with time t for a small sized spherical body falling vertically in a long column of viscous liquid.
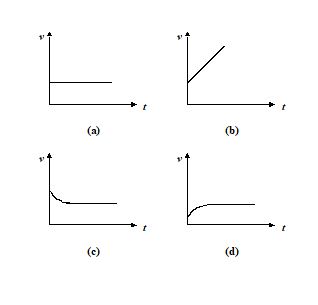
Ans. (d)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
