Video Lecture
Theory For Making Notes
SURFACE TENSION
Introduction
The surface of a liquid behaves somewhat like a stretched elastic membrane. Just as a stretched elastic membrane has a natural tendency to contract and occupy a minimum area, so also the surface of a liquid has got the natural tendency to contract and occupy a minimum possible area as permitted by the circumstances of the liquid mass. We have many evidences in support of this fact, which we discuss now
(i)
We very often find that a small quantity of a liquid spontaneously takes a spherical shape, e.g., rain drops, small quantities of mercury placed on a clean glass plate etc. Now, for a given volume, a sphere has the least surface area. Thus, this fact shows that a liquid always tends to have the least surface area.
(ii)
If we immerse a camel-hair brush in water, its hairs spread out, but the moment it is taken out of water, they all cling together as though bound by some sort of elastic thread.
Experimental demonstration: Make a circular loop of wire and dip it in a soap solution. Take it out of the solution and find a thin film of soap solution across the loop. Place a moistened cotton loop gently on the film. The thread will lie on the film in an irregular manner as shown in figure (a).
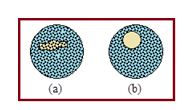
Now prick the film inside the cotton thread loop by a pin. At once the thread will spontaneously take the shape of a circle as shown in figure (b). The thread has a fixed perimeter. For a given perimeter a circle has got the maximum area. Hence the remaining portion of the film occupies the minimum area.
Definition of Surface Tension
The above evidences and experiment prove beyond doubt that the surface of a liquid behaves like a stretched elastic membrane having a natural tendency to contract and occupy a minimum possible area as permitted by the circumstances of the liquid mass. It is defined as “the property of the surface of a liquid by virtue of which it tends to contract and occupy the minimum possible area is called surface tension andis measured by the force per unit length of a line drawn on the liquid surface, acting perpendicular to it and tangentially to the surface of the liquid”.
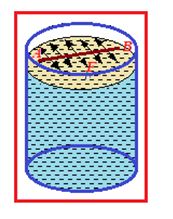
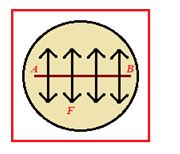
Let an imaginary line AB on the surface of liquid of length L as shown in figure and force on this line is F, So surface tension
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellu
T=\frac{F}{L}
Surface tension has dimensions [MT–2] and Its unit is Newton per metre (Nm–1).
It depends on temperature. The surface tension of all liquids decreases linearly with temperature
It is a scalar quantity and become zero at a critical temperature.
Factors Affecting Surface Tension
(1) Temperature :
The surface tension of liquid decreases with rise of temperature. The surface tension of liquid is zero at its boiling point and it vanishes at critical temperature. At critical temperature, intermolecular forces for liquid and gases becomes equal and liquid can expand without any restriction.
(2) Impurities :
The presence of impurities either on the liquid surface or dissolved in it, considerably affect the surface tension, depending upon the degree of contamination. A highly soluble substance like sodium chloride when dissolved in water, increases the surface tension of water. But the sparingly soluble substances like phenol when dissolved in water, decreases the surface tension of water.
Illustration
Calculate the force required to take away a flat circular plate of radius 4 cm from the surface of water, surface tension of water being 75 dyne cm–1.
Solution:
Length of the surface = circumference of the circular plate
= 2 \displaystyle \pi r = (8 \displaystyle \pi ) cm
Required force 72 x 8 \displaystyle \pi = 1810 dyne
Molecular theory of surface tension
The surface tension of a liquid arises out of the attraction of its molecules. Molecules of a fluid (liquid and gas) attract one another with a force. It depends on the distance between molecules. The distance up to which the force of attraction between two molecules is appreciable is called the molecular range, and is generally of the order of 10–9 metre. A sphere of radius equal to the molecular range drawn around a molecule is called sphere of influence of the molecules lying within the sphere of influence.
Consider three molecules A, B and C having their spheres of influence as shown in the figure. The sphere of influence of A is well inside the liquid, that of B partly outside and that of C exactly half of total
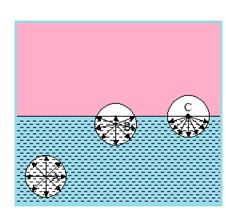
Molecules like A do not experience any resultant force, as they are attracted equally in all directions. Molecules like B or C will experience a resultant force directed inward. Thus the molecules well inside the liquid will have only kinetic energy but the molecules near the surface will have kinetic energy as well as potential energy which is equal to the work done in placing them near the surface against the force of attraction directed inward.
Surface energy
Any strained body possesses potential energy, which is equal to the work done in bringing it to the present state from its initial unstrained state. The surface of a liquid is also a strained system and hence the surface of a liquid also has potential energy, which is equal to the work done in creating the surface. This energy per unit area of the surface is called surface energy.
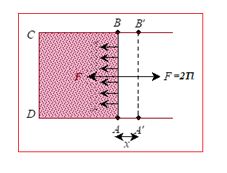
To derive an expression for surface energy consider a wire frame equipped with a sliding wire AB as shown in figure. A film of soap solution is formed across ABCD of the frame. The side AB is pulled to the left due to surface tension. To keep the wire in position a force F, has to be applied to the right. If T is the surface tension and l is the length of AB, then the force due to surface tension over AB is 2lT to the left because the film has two surfaces (upper and lower).
Since the film is in equilibrium, F = 2lT
Now, if the wire AB is pulled to the right, energy will flow from the agent to the film and this energy is stored as potential energy of the surface created just now. Let the wire be pulled slowly through x.
Then the work done = energy added to the film from the agent = F.x = 2lTx
Potential energy per unit area (Surface energy) of the film = \frac{{2lTx}}{{2lx}}=T
Thus surface energy of the film is numerically equal to its surface tension.
Its unit is joule per square metre (Jm-2).
Illustration
Calculate the work done in blowing a soap bubble of radius 10 cm, surface tension being 0.06 Nm–1. What additional work will be done in further blowing it so that its radius is doubled?
Solution:
In case of a soap bubble, there are two free surfaces.
Work done in blowing a soap bubble of radius R is given by,
W = 2 X 4 \displaystyle \pi R2xT, where T is the surface tension of the soap solution.
where R = 0.1 m, T = 0.06 Nm–1
W’ = 8 \displaystyle \pi (0.1)2´ 0.06 J = 1.51 J
Similarly, work done in forming a bubble of radius 0.2 m is,
W = 8 \displaystyle \pi (0.2)2X 0.06 J = 6.03 J
Additional work done in doubling the radius of the bubble is given by,
W’– W = 6.03 J – 1.51 J = 4.52 J
Illustration
A film of soap is formed on a rectangular frame of length 10 cm dipping into a soap solution. The frame hangs from the arm of a balance. An extra weight of 0.42 g must be placed in the opposite pan to balance the pull of the frame. Calculate the surface tension of the soap solution.
Solution:
Since the film has two surface, the force of surface tension will be given by
F = 2 x 10 xT = 20 T,
where T is surface tension of soap solution.
The force is balanced by 0.42 g wt.
0.42 x 980 = 20 T or T=\frac{{0.42\times 980}}{{20}} = 20.6 dyne/cm
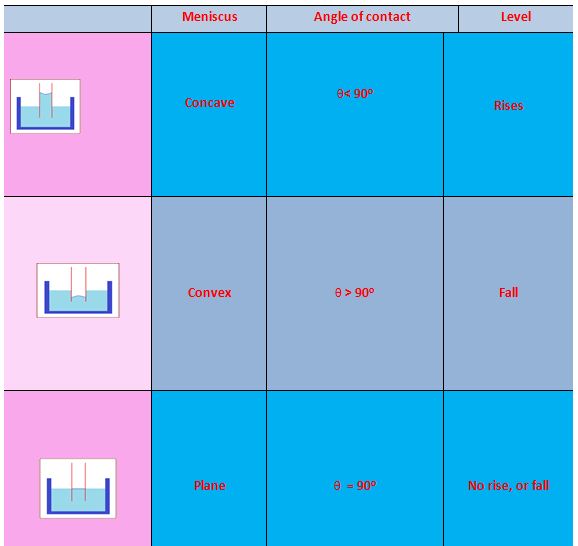
Angle of Contact
When a solid body in the form of a tube or plate is immersed in a liquid, the surface of the liquid near the solid is, in general, curved. It is defined as the angle between the tangents to the liquid surface and the solid surface at the point of contact, for that pair of solid and liquid is called angle of contact.
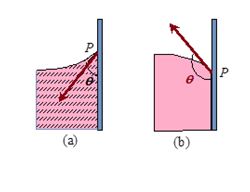
For example when glass strip is dipped in water and mercury as shown in figure (a) and (b) respectively, the angle \displaystyle \theta is angle of contact, which is acute in case of water and obtuse in case of mercury.
Excess Pressure
The pressure inside a liquid drop or a soap bubble must be in excess of the pressure outside the bubble drop because without such pressure difference a drop or a bubble cannot be in stable equilibrium. Due to surface tension the drop or bubble has got the tendency to contract and disappear altogether. To balance this, there must be an excess of pressure inside the bubble.
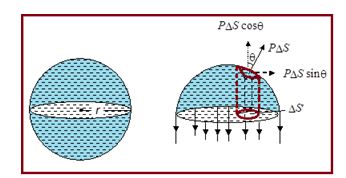
To obtain a relation between the excess of pressure and the surface tension, consider a water drop of radius r and surface tension T. Divide the drop into two halves by a horizontal plane passing through its center as shown in figure and consider the equilibrium of one-half, say, the upper half. The forces acting on it are:
(i)
forces due to surface tension distributed along the circumference of the section.
(ii)
outward thrusts on elementary areas of it due to excess pressure.
Obviously, both the types of forces are distributed. The first type of distributed forces combine into a force of magnitude 2 \displaystyle \pi r´T. To find the resultant of the other type of distributed forces, consider an elementary area \displaystyle \Delta S of the surface. The outward thrust on \displaystyle \Delta S = p \displaystyle \Delta S where p is the excess of the pressure inside the bubble. If this thrust makes an angle \displaystyle \theta with the vertical, then it is equivalent to \displaystyle \Delta Sp cos \displaystyle \theta along the vertical and \displaystyle \Delta Sp sin \displaystyle \theta along the horizontal. The resolved component \displaystyle \Delta Sp sin \displaystyle \theta is ineffective as it is perpendicular to the resultant force due to surface tension. The resolved component \displaystyle \Delta Sp cos \displaystyle \theta contributes to balancing the force due to surface tension.
The resultant outward thrust = S \displaystyle \Delta Sp cos \displaystyle \theta
= pS \displaystyle \Delta S cos \displaystyle \theta
= pS \displaystyle \Delta S’ where \displaystyle \Delta S’ = \displaystyle \Delta S cos \displaystyle \theta
= area of the projection of \displaystyle \Delta S on the horizontal dividing plane
= p´ \displaystyle \pi r2 (QS \displaystyle \Delta S¢ = \displaystyle \pi r2)
For equilibrium of the bubble we have
\displaystyle \pi r2p = 2 \displaystyle \pi r.T
or, p=\frac{{2T}}{r}
If it is a soap bubble, the resultant force due to surface tension is 2 \displaystyle \pi r.2T, because a bubble has two surfaces. Hence for the equilibrium of a bubble we have
\displaystyle \pi r2p = 4 \displaystyle \pi rT
or, p=\frac{{4T}}{r}
Illustration
Find the difference in the air pressure between the inside and outside of a soap bubble, 5 mm in diameter. Assume surface tension to be 1.6 Nm–1.
Solution:
Excess pressure = \frac{{4\,T}}{r}, where r is radius of curvature of the surface.
Required pressure difference = \frac{{4\times 1.6}}{{2.5\times {{{10}}^{{-3}}}}} = 2560 Nm-2
Illustration
If a number of little droplets of water, all of the same radius r coalesce to form a single drop of radius R, Show that the rise in temperature of the water is given by, \frac{{3\sigma }}{J}\,\left( {\frac{1}{r}\,-\,\frac{1}{R}} \right)where J is the mechanical equivalent of heat, and s is the surface tension of water.
Solution:
Let n be the number of droplets, each of radius r cm that coalesce to form a single drop of radius R cm.
Decrease in the surface area = 4 \displaystyle \pi r2n– 4 \displaystyle \pi R2
Decrease in the surface energy = (4 \displaystyle \pi r2n– 4 \displaystyle \pi R2) s
Heat energy produced in the drop = \frac{{4\pi \sigma }}{J}\ (n{{r}^{2}}-{{R}^{2}})
Suppose the whole of heat energy is used to raise the temperature of the resultant drop by \displaystyle \theta , therefore, mS \displaystyle \theta = \frac{{4\pi \sigma }}{J}\ (n{{r}^{2}}-{{R}^{2}}),
where m is the mass of the drop having specific heat S.
m=\frac{4}{3}\pi {{R}^{3}}\times 1 (density = 1 gm/cc)
S = 1 cal/g°C for water
\theta =\frac{{4\pi \sigma }}{J}\ (n{{r}^{2}}-{{R}^{2}})\times \frac{3}{{4\pi {{R}^{3}}}}=\frac{{3\sigma }}{J}\,\left( {\frac{{n{{r}^{2}}}}{{{{R}^{3}}}}-\frac{1}{R}} \right) …(i)
Since volume remains the same, n\frac{4}{3}\ \pi {{r}^{3}}=\frac{4}{3}\ \pi {{R}^{3}} or n={{\left( {\frac{R}{r}} \right)}^{3}}
Putting this value in (i), we have \theta =\frac{{3\sigma }}{J}\ \left( {\frac{{{{R}^{3}}}}{{{{r}^{3}}}}\times \frac{{{{r}^{2}}}}{{{{R}^{3}}}}-\frac{1}{R}} \right)=\frac{{3\sigma }}{J}\ \left( {\frac{1}{r}-\frac{1}{R}} \right)
Thus the rise in temperature is given by, \text{ }\!\!\theta\!\!\text{ }=\frac{{\text{3 }\!\!\sigma\!\!\text{ }}}{\text{J}}\ \left( {\frac{\text{1}}{\text{r}}-\frac{\text{1}}{\text{R}}} \right)
Capillary action
When a glass tube of very fine bore called a capillary tube is dipped in a liquid (like water,) the liquid immediately rises up into it due to the surface tension. This phenomenon of rise of a liquid in a narrow tube is known as capillarity.
Suppose that a capillary tube of radius r is dipped vertically in a liquid. The liquid surface meets the wall of the tube at some inclination \displaystyle \theta called the angle of contact. Due to surface tension a force, \displaystyle \Delta lT acts on an element \displaystyle \Delta l of the circle of contact along which the liquid surface meets the solid surface and it is tangential to the liquid surface at inclination \displaystyle \theta to the wall of the tube. (The liquid on the wall of the tube exerts this force. By the third law of motion, the tube exerts the same force on the liquid in the opposite direction.) Resolving this latter force along and perpendicular to the wall of the tube, we have \displaystyle \Delta lTcos \displaystyle \theta along the tube vertically upward and \displaystyle \Delta lTsin \displaystyle \theta perpendicular to the wall. The latter component is ineffective. It simply compresses the liquid against the wall of the tube. The vertical component \displaystyle \Delta lTcos \displaystyle \theta pulls the liquid up the tube.
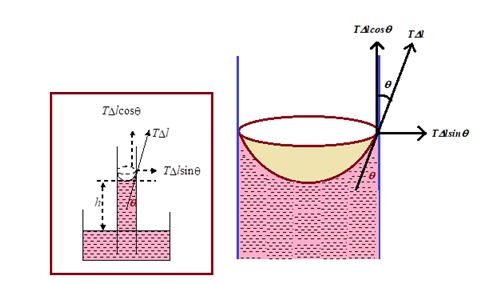
The total vertical upward force = S \displaystyle \Delta lTcos \displaystyle \theta = T cos \displaystyle \theta S \displaystyle \Delta l = T cos \displaystyle \theta 2 \displaystyle \pi r
(∑ \displaystyle \Delta [/katex = 2 \displaystyle \pi r).
Due to this upward pull liquid rises up in the capillary tube till it is balanced by the downward gravitational pull. If h is the height of the liquid column in the tube up to the bottom of the meniscus and v is the volume of the liquid above the horizontal plane touching the meniscus at the bottom, the gravitational pull, i.e., weight of the liquid inside the tube is ( \displaystyle \pi r2h + v) rg.
For equilibrium of the liquid column in the tube 2 \displaystyle \pi rT cos \displaystyle \theta = ( \displaystyle \pi r2h + v) rg.
If volume of the liquid in meniscus is negligible then, 2 \displaystyle \pi rT cos \displaystyle \theta = ( \displaystyle \pi r2h) rg.
h=\frac{{2T\cos \theta }}{{r\rho g}}
The small volume of the liquid above the horizontal plane through the lowest point of the meniscus can be calculated if \displaystyle \theta is given or known. For pure water and glass \displaystyle \theta = 0° and hence the meniscus is hemispherical.
v = volume of the cylinder of height r– volume of hemisphere.
= \pi {{r}^{3}}-\frac{1}{2}\frac{{4\pi }}{3}{{r}^{3}} = \pi {{r}^{3}}-\frac{2}{3}\ \pi {{r}^{3}}=\frac{1}{3}\pi {{r}^{3}}
For water and glass
2\pi rT=\left( {\pi {{r}^{2}}h\,+\,\frac{{\pi {{r}^{3}}}}{3}} \right)\,\,\rho g
2T = r \left( {h\,+\,\frac{r}{3}} \right)\,\rho \,g
h\,=\,\frac{{\text{2}T}}{{r\,\text{ }\!\!\rho\!\!\text{ }\,g}}\,\,-\,\frac{r}{\text{3}}
For a given liquid and solid at a given place as r, T, \displaystyle \theta and g are constant,
hr = constant
i.e., lesser the radius of capillary greater will be the rise and vice-versa.
Illustration
Water rises to a height of 10 cm in a certain capillary tube. The level of mercury in the same tube is depressed by 3.42 cm. Compare the surface tensions of water and mercury. Specific gravity of mercury is 13.6 g/cc and angle of contact for water and mercury are zero and 135° respectively.
Solution:
Using the capillarity relation, T = \frac{{r\,h\,\rho \,g}}{{2\cos \theta }}
T1 (for water) = \frac{{r\times 1\times g\times 10}}{{2\cos \theta }} = 5rg
T2 (for mercury) = \frac{{r\times 13.6\times g\times \,\,(-3.42)}}{{2\cos 135{}^\circ }} = \frac{{r\times 13.6\times g\times \ (-3.42)}}{{2\times \left( {\frac{{-1}}{{\sqrt{2}}}} \right)}} = 32.9 rg
\frac{{{{T}_{1}}}}{{{{T}_{2}}}}=\frac{{5\ rg}}{{32.9\ rg}}=\frac{1}{{6.5}}= 0.15
Illustration
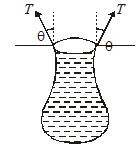
A vessel, whose bottom has round holes with diameter of 1 mm is filled with water. Assuming that surface tension acts only at holes, find the maximum height to which the water can be filled in the vessel without leakage. Given that surface tension of water is 75 × 10–3 N/m and g = 10 m/s2.
Solution:
As shown in figure here the vertical force due to surface tension at the hole T cos q × L = T cos q × 2 \displaystyle \pi r will balance the weight mg, i.e. \displaystyle \pi r2h \displaystyle \rho g, i.e.,
T\cos \theta =2\pi r=\pi {{r}^{2}}h\rho g
or, h=(2T\cos \theta /\rho rg)
This h will be max when \cos \theta =\max =1
So, {{(h)}_{{\max }}}=\frac{{2\times 75\times {{{10}}^{{-3}}}}}{{{{{10}}^{3}}\times 5\times {{{10}}^{{-4}}}\times 10}}=0.03\text{m}=3\,\text{cm}
Illustration
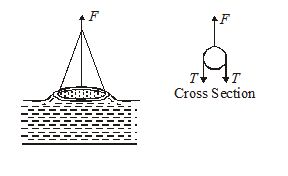
A ring is cut from a platinum tube of 8.5 cm internal and 8.7 cm external diameter. It is supported horizontally from a pan of a balance so that it comes in contact with the water in a glass vessel. What is the surface tension of water if an extra 3.97 g weight is required to pull it away from water? (g = 980 cm/s2).
Solution:
The ring is in contact with water along its inner and outer circumference; so when pulled out the total force on it due to surface tension will be
F=T(2\pi {{r}_{1}}+2\pi {{r}_{2}})
so T=\frac{{mg}}{{2\pi ({{r}_{1}}+{{r}_{2}})}} [as F = mg]
i.e., T=\frac{{3.97\times 980}}{{3.14\times (8.5\times 8.7)}}=72.13\ \text{dyne/cm}
Illustration
The lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube to blow a bubble at its end in water? Also calculate the excess pressure. [Surface tension of water = 73 × 10–3 N/m, density of water = 103 kg/m3, 1 atmosphere = 1.01 × 105 Pa and g = 9.8 m/s2].
Solution:
As the bubble is in water, it has only one surface.
So p={{p}_{{in}}}-{{p}_{{out}}}=\frac{{2T}}{r}=\frac{{2\times 7.3\times {{{10}}^{{-2}}}}}{{{{{10}}^{{-3}}}}}=146\text{Pa}
Now as bubble is at a depth of 8 cm in water,
{{p}_{{out}}}={{p}_{{at}}}+h\rho g
So that {{p}_{{in}}}=p+{{p}_{{out}}}=p+{{p}_{{at}}}+h\rho g
i.e., {{p}_{{in}}}=146+1.01\times {{10}^{5}}+8\times {{10}^{{-2}}}\times {{10}^{3}}\times 9.8=1.02\times {{10}^{5}}\text{Pa}
Illustration
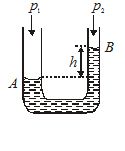
The limbs of a manometer consist of uniform capillary tubes of radii 1.4 × 10–3 m and 7.2 × 10–4 m. Find out the correct pressure difference if the level of the liquid (density 103 kg/m3, surface tension 72 × 10–3 N/m) in narrower tube stands 0.2 m above that in the broader tube.
Solution:
If p1 and p2 are the pressures in the broader and narrower tubes of radii r1 and r2 respectively, the pressure just below the meniscus in respective tubes will be
{{p}_{1}}-\frac{{2T}}{{{{r}_{1}}}} and {{p}_{2}}-\frac{{2T}}{{{{r}_{2}}}}
So, that \left[ {{{p}_{1}}-\frac{{2T}}{{{{r}_{1}}}}} \right]-\left[ {{{p}_{2}}-\frac{{2T}}{{{{r}_{2}}}}} \right]=h\rho g
or {{p}_{1}}-{{p}_{2}}=h\rho g-2T\left[ {\frac{1}{{{{r}_{2}}}}-\frac{1}{{{{r}_{1}}}}} \right]
Assuming the angle of contact to be zero, i.e., radius of meniscus equal to that of capillary,
{{p}_{1}}-{{p}_{2}}=0.2\times {{10}^{3}}\times 9.3-2\times 72\times {{10}^{{-3}}}\left[ {\frac{1}{{7.2\times {{{10}}^{{-4}}}}}-\frac{1}{{14\times {{{10}}^{{-4}}}}}} \right]
or {{p}_{1}}-{{p}_{2}}=1960-97=1863\ \text{Pa}\text{.}
Illustration
Two separate air bubbles (radii 0.002 m and 0.004 m) formed of the same liquid (surface tension 0.07 N/m) come together to form a double bubble. Find the radius and the sense of curvature of the internal film surface common to both the bubbles.
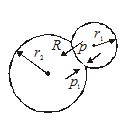
Solution
If r1 and r2 are the radii of smaller and larger bubble and p0 is the atmospheric pressure, the pressure inside them will be
{{p}_{1}}={{p}_{0}}+\frac{{4T}}{{{{r}_{1}}}} and {{p}_{2}}={{p}_{0}}+\frac{{4T}}{{{{r}_{2}}}} …(i)
Now as the pressure inside the smaller bubble will be more than inside the larger bubble, so for interface,
p={{p}_{1}}-{{p}_{2}} …(ii)
Now as excess pressure acts from concave to convex side, the interface will be concave towards smaller bubble and convex towards larger bubble. (as shown in figure) and if R is the radius of interface,
p=(4T/R) …(iii)
So substituting equation (i) and (iii) in (ii), we get
\frac{{4T}}{R}=4T\left[ {\frac{1}{{{{r}_{1}}}}-\frac{1}{{{{r}_{2}}}}} \right], i.e., R=\frac{{{{r}_{1}}{{r}_{2}}}}{{({{r}_{2}}-{{r}_{1}})}}
So here R=\frac{{0.002\times 0.004}}{{0.004-0.002}}=0.004\,\text{m}.
Illustration
A drop of water of volume V is pressed between two glass plates so that it spreads to an area A. If T is surface tension, then the normal force required to separate the glass plates is
(a) \frac{{T{{A}^{2}}}}{V}
(b) \frac{{T{{A}^{2}}}}{{2V}}
(c) \frac{{2T{{A}^{2}}}}{V}
(d) \frac{{4T{{A}^{2}}}}{V}
Solution
Excess pressure P=\frac{T}{R}
R=\frac{d}{2}
P=\frac{{2T}}{d}
P=\frac{{2TA}}{V} \left[ {\therefore \,\,\,d=\frac{V}{A}} \right]
Force = Pressure ´ Area =\frac{{2T{{A}^{2}}}}{V}
(c)
Practice Questions (Basic Level)
Q.1
n drops of a liquid, each with surface energy E, join to form a single drop.
(a) Some energy will be released in the process.
(b) Some energy will be absorbed in the process.
(c) The energy released or absorbed will be E\left( {n-{{n}^{{2/3}}}} \right)
(d) The energy released or absorbed will be nE\left( {{{2}^{{2/3}}}-1} \right)
Ans. (a,c)
Q.2
A number of water droplets each of radius r coalesce to form a bigger drop of radius R. The rise in temperature is
(a) 3T/RJ
(b) 3T/rJ
(c) \frac{{3T}}{J}\left( {\frac{1}{r}+\frac{1}{R}} \right)
(d) \frac{{3T}}{J}\left( {\frac{1}{r}-\frac{1}{R}} \right)
Ans. (c)
Q.3
Water rises in a vertical capillary tube upto a length of 10 cm. If the tube is inclined at 45o, the length of water risen in the tube will be
(a) 10 cm
(b) 10 \sqrt{2} cm
(c) 10/\sqrt{2} cm
(d) none of these
Ans. (b)
Q.4
A U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of 1.5 ´ 10-2N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
(a) 2.5 ´ 10-2 Nm-1
(b) 0.46 ´ 10-2 Nm-1
(c) 1.78 ´ 10-2 Nm-1
(d) 2.70 ´ 10-2 Nm-1
Ans (a)
Q.5
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20o C) is 2.50 ´ 10-2 Nm-1? If an air bubble of the same dimensions were formed at a depth of 40.0 cm inside a container containing soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atm. is 1.01 ´ 105 Pa).
(a) 20 Pa, 0.466 ´ 105 Pa
(b) 20 Pa, 1.06 ´ 105 Pa
(c) 50 Pa, 1.06 ´ 105 Pa
(d) 10 Pa, 0.12 ´ 105 Pa
Ans (b)
Q.6
In the figure, three soap bubbles A, B and C prepared by blowing the capillary tube with stop clocks S, S1, S2 and S3. With stop cocks S closed and S1, S2 and S3 open
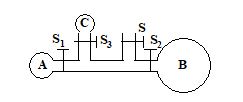
(a) C and A will both start collapsing with volume of B increasing
(b) B will start collapsing with volumes of A and C increasing
(c) C will start collapsing with volumes of A and B increasing
(d) volumes of A, B and C will become equal at equilibrium
Ans. (a)
Q.7
Which of the following graphs may represent the relation between the capillary rise h and the radius r of the capillary?
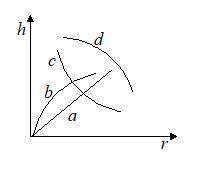
Ans. (c)
Q.8
Figure shows a capillary tube of radius r dipped into water. If the atmospheric pressure is Po, the pressure at point A is (S is surface tension of liquid)
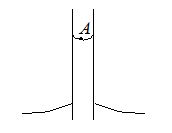
(a) {{P}_{o}}
(b) {{P}_{o}}+\frac{{2S}}{r}
(c) {{P}_{o}}-\frac{{2S}}{r}
(d) {{P}_{o}}-\frac{{4S}}{r}
Ans. (c)
Practice Questions (JEE Main Level)
Q.1
A drop of water of volume V is pressed between two glass plates so that it spreads to an area A. If T is surface tension, then the normal force required to separate the glass plates is
(a) \frac{{T{{A}^{2}}}}{V}
(b) \frac{{T{{A}^{2}}}}{{2V}}
(c) \frac{{2T{{A}^{2}}}}{V}
(d) \frac{{4T{{A}^{2}}}}{V}
Ans. (c)
Q.2
Two soap bubbles of radius 3 cm and 4 cm coalesce to form a simple bubble under isothermal conditions. Then the radius of bigger bubble is
(a) 7 cm (b) 1 cm (c) 12 cm (d) 5 cm
Ans. (d)
Q.3
The limbs of a manometer consists of uniform capillary tubes of radii 1.4 ´ 10-3 m and
7.2 ´ 10-4 m. Find out the correct pressure difference if the level of the liquid (density 103 kg/m3, surface tension 72 ´ 10-3 N/m) in narrower tube stands 0.2 m above that in the broader tube.
(a) 1863 Pa
(b) 1890 Pa
(c) 1900 Pa
(d) 2000 Pa
Ans (a)
Q.4
A water film is made between two parallel wires of length 10 cm and at a distance of 0.5 cm from each other. If the distance between the wires is increased by 1mm, how much work will be done? (Surface tension of water = 72 dyne/cm).
(a) 144 erg
(b) 150 erg
(c) 160 erg
(d) 200 erg
Ans (a)
Q.5
A container of width 2a is filled with a liquid. A thin wire of weight per unit length l is gently placed over the liquid surface in the middle of the surface as shown in the figure. As a result, the liquid surface is depressed by a distance y (y<<a). Determine the surface tension of the liquid.
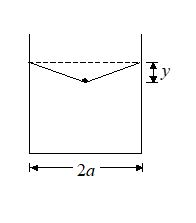
(a) \frac{{\lambda a}}{{2y}}
(b) \frac{{\lambda a}}{{3y}}
(c) \frac{{\lambda a}}{{y}}
(d) \frac{{\lambda a}}{{5y}}
Ans (a)
Practice Questions (JEE Advance Level)
Q.1
The end of a capillary tube with a radius r is immersed in water. Is mechanical energy conserved when the water rises in the tube? The tube is sufficiently long. If not, calculate the energy change.
(a) Energy loss = 2pT5/rg
(b) Energy loss = 2pT2/rg
(c) Energy loss = 2pT2/2rg
(d) Energy loss = 2pT2/3rg
Ans (b)
Q.2
A soap bubble is being blown at the end of a very narrow tube of radius b. Air (density r) moves with a velocity v inside the tube and comes to rest inside the bubble. The surface tension of the soap solution is T. After some time the bubble, having grown to a radius r, separates from the tube. Find the value of r. Assume that r >>b so that your can consider the air to be falling normally on the bubble’s surface.
(a) \frac{{T}}{{\rho {{v}^{2}}}}
(b) \frac{{4T}}{{\rho {{v}^{3}}}}
(c) \frac{{4T}}{{\rho {{v}^{2}}}}
(d) \frac{{12T}}{{\rho {{v}^{7}}}}
Ans (c)
Q.3
When a vertically capillary of length l with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is r, the inside diameter of the capillary is d, the contact angle is q, the atmospheric pressure is po. Find the surface tension of liquid.
(a) \left( {\rho gh+\frac{{{{P}_{o}}l}}{{l-h}}} \right)\frac{d}{5}\cos \theta
(b) \left( {\rho gh+\frac{{{{P}_{o}}l}}{{l-h}}} \right)\frac{d}{4}\cos \theta
(c) \left( {2\rho gh+\frac{{{{P}_{o}}l}}{{l-h}}} \right)\frac{d}{4}\cos \theta
(d) \left( {2\rho gh+\frac{{{{P}_{o}}l}}{{l+h}}} \right)\frac{{2d}}{4}\cos \theta
Ans (b)
Q.4
Find the lifetime of a soap bubble of radius R connected with the atmosphere through a capillary of length l and inside radius r. The surface tension is T, the viscosity coefficient of the gas is h.
(a) t=\frac{{5\eta l{{R}^{4}}}}{{T{{r}^{4}}}}
(b) t=\frac{{2\eta l{{R}^{3}}}}{{T{{r}^{4}}}}
(c) t=\frac{{5\eta l{{R}^{4}}}}{{T{{r}^{3}}}}
(d) t=\frac{{2\eta l{{R}^{4}}}}{{T{{r}^{4}}}}
Ans (d)
