Video Lecture
Theory For Making Notes
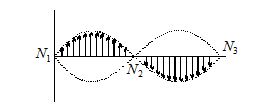
Stationary waves
When two waves of same frequency and same amplitude travel in an opposite directions at same speed, their superposition gives rise to a new type of waves called stationary wave or standing wave. Let the two waves of same amplitude, frequency traveling in opposite direction at same speed are
{{y}_{1}}=a\sin (\omega t-kx) and {{y}_{2}}=a\sin (\omega t+kx)
They by the principle of superposition,
y={{y}_{1}}+{{y}_{2}}=(2a\,\cos \,\,kx).\,\sin \omega t{See the video lecture for detailed solution}
{{y}_{1}}=A\,\sin \omega t [where A\,=2\,a\cos kx]
As this equation satisfies the wave equation \frac{{{{d}^{2}}y}}{{d{{x}^{2}}}}=\frac{{-1}}{{{{v}^{2}}}}\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}}, so it represents a wave. However as it is not of the form of f(ax\pm bt). The wave is not traveling and so it is called standing wave.
The amplitude of the wave =A=2\,a\cos kxis NOT constant but varies periodically with position.
The points for which amplitude is minimum are called nodes and for these \cos \,kx=0
kx=\pm \frac{\pi }{2},\,\,\pm \frac{{3\pi }}{2},\,\,\pm \frac{{5\pi }}{2},\,\,\pm \frac{{7\pi }}{2}……
or x=\pm \frac{\lambda }{4},\,\,\pm \frac{{3\lambda }}{4},\,\,\pm \frac{{5\lambda }}{4},\,……
This shows that all the nodes are equally spaced and the spacing between two adjacent nodes is \lambda /2 with {{A}_{{\min }}}=0. Nodes are permanently at rest.
The points for which amplitude is maximum are called antinodes. For these \cos \,kx=\pm 1 i.e., kx=0,\,\,\,\,\pm \pi ,\,\,\,\,\mp 2\pi ,\,\,\,\,\pm 3\pi …..
x=0,\,\,\pm \frac{\lambda }{2},\,\,\frac{{2\lambda }}{2},\,\,\frac{{3\lambda }}{2}…..
Like nodes anitinodes are also equispaced with space (\lambda /2) and {{(A)}_{{\max }}}=\pm \,\,2A. Further node and antinode are separated with spacing \lambda /4.
Certain features
1.
The standing wave is confined to a particular region between the staring point and reflecting point of the wave.
2.
There is no onward motion of the wave from one particle to the adjoining particle and so on beyond this particular region.
3.
The total energy associated with a stationary wave is twice the energy of each of incident and reflected wave.
4.
There are certain points in the medium in a standing wave, which are permanently at rest called node.
5.
In a standing wave, the medium splits up into a number of segments. Each segment is vibrating up and down as a whole.
6.
All the particles in one particular segment vibrate in the same phase and particles in two consecutive segments are differ in phase by 180°.
7.
All the particles except those at nodes execute SHM about their mean positions with same time period.
8.
The amplitude of vibration of particles varies from zero at nodes to maximum at antinodes.
9.
Velocity of particles while crossing mean position varies from maximum at antinodes to zero at nodes.
Reflection and Refraction/Transmission of Wave
Effect on different variables : In case of reflection, because medium is same and hence, speed, frequency (w) and wavelength l (or k) do not changes.
On the other hand in case of transmitted wave since medium changes and hence speed, wavelength (or k) changes but frequency (w) remains the same.
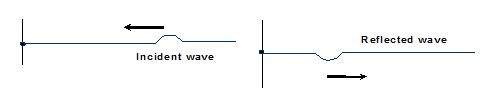
Boundary conditions : Reflection of a wave pulse from some boundary depends on the nature of the boundary.
(a)
Waves on reflection from a fixed end undergo a phase change of 180°
(b)
A wave reflected from a free end returns without a change in phase.

(c)
In case of a pressure wave, there is no phase change when reflected from a denser medium or fixed end and there is phase change by p when reflected from rarer medium.
(d)
Wave in a combination of string
(i) Wave goes from rarer to denser medium
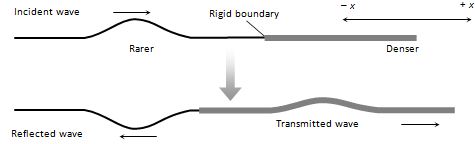
Incident wave {{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)
Reflected wave {{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+\pi ] =-\,a\sin \,(\omega \,t+{{k}_{1}}x)
Transmitted wave {{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)
(ii) Wave goes from denser to rarer medium
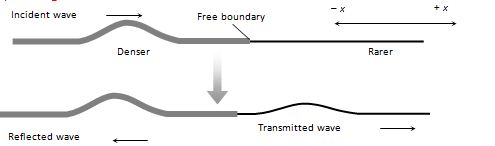
Incident wave {{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)
Reflected wave {{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+0] =\,a\sin \,(\omega \,t+{{k}_{1}}x)
Transmitted wave {{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)
(iii) Ratio of amplitudes : It is given as follows
\frac{{{{a}_{r}}}}{{{{a}_{i}}}}=\frac{{{{k}_{1}}-{{k}_{2}}}}{{{{k}_{1}}+{{k}_{2}}}}=\frac{{{{v}_{2}}-{{v}_{1}}}}{{{{v}_{2}}+{{v}_{1}}}} and \frac{{{{a}_{t}}}}{{{{a}_{i}}}}=\frac{{2{{k}_{1}}}}{{{{k}_{1}}+{{k}_{2}}}}=\frac{{2{{v}_{2}}}}{{{{v}_{1}}+{{v}_{2}}}}
Harmonics in a Stretched string
When a string under tension is set into vibrations, then transverse harmonic wave propagate along its length. When the length is finite, then reflected waves also exist. The incident and reflected waves will superimpose to produce transverse stationary waves in the string.
First Harmonic Or Fundamental note
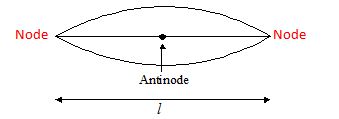
Let length of string be l and N to AN=\lambda /4 and AN to N=\lambda /4
N to N=\frac{\lambda }{4}+\frac{\lambda }{4}=\frac{{2\lambda }}{4}=\frac{\lambda }{2}
Equating \frac{\lambda }{2}=l,\,\,\,\,\lambda =2l
Now, V=f\lambda ,\,\,\,\,f=\frac{V}{\lambda }=\frac{V}{{2l}}
But velocity in case of stretched string is given by V=\sqrt{{\frac{T}{m}}}
Where T= tension in string.
m=mass per unit length.
= linear mass density.
f=\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}
This is the minimum possible frequency that we can have. This frequency is called as fundamental frequency.
Second Harmonic Or First overtone
At the fixed end, node is always formed because that ends cannot vibrate at all.
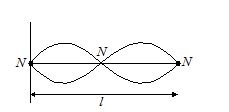
Distance in terms of wavelength =4\cdot \,\frac{\lambda }{4}=\lambda and geometrical length =l. Therefore
\lambda =l,\,\,V=f\lambda ,\,\,\,\,\,\,{{f}_{1}}=\frac{V}{l}=\frac{{2V}}{{2l}}=2\cdot \left[ {\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}} \right]=2 [Fundamental frequency]
Since it is twice of times the fundamental frequency, so this frequency is called as 2nd (second) harmonic.
Third Harmonic Or Second overtone
Distance in term of wavelength =\frac{{6\lambda }}{4}=\frac{{3\lambda }}{2}
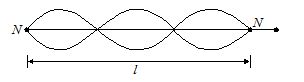
Geometrical length =l
\frac{{3\lambda }}{2}=l\,\,\,\,\,\,\,\,\,\,\,\lambda =\frac{{2l}}{3} {{f}_{2}}=\frac{V}{\lambda }=\frac{V}{{\frac{{2\lambda }}{3}}}=\frac{{3V}}{{2l}}=3.\frac{1}{{2l}}\sqrt{{\frac{T}{m}}} =3 [Fundamental frequency]
Since this frequency {{f}_{2}} is 3 times the fundamental frequency. Therefore this is called as 3rd [third] harmonic.
If we continue in the same way, we get the series of frequencies which is
\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}→ fundamental frequency → zero overtone.
\frac{2}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,2ndHarmonic \xrightarrow{{}}\,\,1st\,\,overtone
\frac{3}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,3rd Harmonic \xrightarrow{{}}\,\,2nd\,\, overtone
\frac{4}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,4th Harmonic \xrightarrow{{}}\,\,3rd\, overtone
\frac{5}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,5th Harmonic \xrightarrow{{}}\,\,4th\, overtone
All odd and even harmonics are present.
If it vibrates in p loops f=\frac{p}{{2l}}\sqrt{{\frac{T}{m}}}
Law’s of vibration of stretched string f=\frac{p}{{2l}}\sqrt{{\frac{T}{{(Al)d/l}}}}=\frac{p}{{2l}}\sqrt{{\frac{{Tl}}{{\frac{{\pi {{D}^{2}}}}{4}.l.d}}}}=\frac{p}{{2l}}\sqrt{{\frac{{4Tl}}{{\pi {{D}^{2}}\,l.d}}}}
1.
law of length f\propto \,\,\frac{1}{l}
2.
law of tension f\propto \,\,\sqrt{T}
3.
law of diameter f\propto \,\,\frac{1}{D}
4.
law of density f\propto \,\,\frac{1}{{\sqrt{d}}}
Illustration
A sonometer wire has a length of 114 cm between two fixed ends. Where should two bridge be placed so as to divide the wire into three segments whose fundamental frequencies are in the ratio 1 : 3: 4 ?
Solution:
For a specific tension, the fundamental frequency of vibration, f\,\alpha \,\frac{1}{L}
So, for having fundamental frequencies in the ratio of 1 : 3 : 4, the vibrating lengths should be in the ratio 1 : (1/3) : (1/4). That is,
If x is the common factor, we have
12x + 4 x + 3 x = 114 = length of the string
or 19 x = 114 or x = 6
L1 = 12 × 6 = 72 cm
L2 = 4 × 6 = 24 cm
L3 = 3 × 6 = 18 cm
Illustration
The fundamental frequency of a sonometer wire increases by 6 Hz if its tensions is increased by 44% keeping the length constant. Find the change in the fundamental frequency of the sonometer wire, when the length of the wire is increased by 20% keeping the original tension in the wire.
Solution:
The fundamental frequency is given by f\,=\,\frac{1}{{2L}}\,\sqrt{{\frac{T}{m}}}
Keeping the length of given wire constant, we have \frac{{f\prime }}{f}\,=\,{{\left( {\frac{T}{T}} \right)}^{{1/2}}}
here f’ = f + 6 and T’ = T = 0.44 T = 1.44 T,
\frac{{(f\,+\,6)}}{f}\,=\,\sqrt{{\frac{{1.44T}}{T}}}
or f = 30 Hz
Now, keeping the original tension same the length of given wire is changed to
L” = L + 0.020 L = 1.20 L
\frac{{f”}}{f}\,=\,\frac{L}{{L”}}\,=\,\frac{1}{{1.20}} or f “ = \frac{{30}}{{1.2}} = 25 Hz
Δf” – f = 25 – 30 = – 5 Hz
Thus, the fundamental frequency will decrease by 5 Hz.
Standing waves in closed organ pipe
Organ pipes are the numerical instruments, which are used for producing numerical sound by blowing air into the pipe.
Longitudinal standing waves are formed in account of superposition of incident and reflected longitudinal waves.
Organ pipe are of two types:
(i)
Closed organ pipe
(ii)
Open organ pipe
Harmonics in a Closed organ pipe
First Harmonic Or Fundamental note
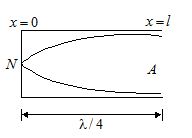
\mathbf{V}=f\lambda ,\,\,\,f=\frac{V}{{4l}}
f=\frac{V}{{4l}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\because \,\,\,\,\,\left( {\frac{\lambda }{4}=l} \right)
This is the minimum possible frequency that we would arrange and it is called as fundamental frequency.
Third Harmonic Or First overtone
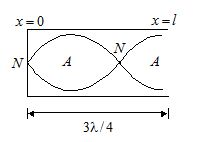
\frac{{3\lambda }}{4}=l), \lambda =\frac{{4l}}{3}
{{f}_{1}}=\frac{{3V}}{{4l}} , {{f}_{2}}=\frac{V}{{4l/3}}
This frequency {{f}_{1}} is 3 times the fundamental frequency. Hence called as 3rd Harmonic
Fifth Harmonic Or Second overtone
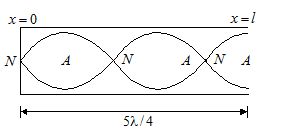
\frac{{5\lambda }}{4}=l
\lambda =\frac{{4l}}{5} {{f}_{2}}=\frac{\mathbf{V}}{{4l/5}}=\left( {\frac{{5\mathbf{V}}}{{4l}}} \right)
This frequency {{f}_{2}} is 5 times the fundamental frequency. Hence called as 5th Harmonic.
In Similar way
We can arrange the further frequencies.
1.
\frac{V}{{4l}} fundamental frequency/zero overtone
2.
\frac{{3V}}{{4l}} 3rd Harmonic/1st overtone
3.
\frac{{5V}}{{4l}} 5th Harmonic/2nd overtone
4.
\frac{{7V}}{{4l}} 7th Harmonic/3rd overtone
5.
\frac{{9V}}{{4l}} 9th Harmonic/4th overtone
6.
\frac{{11V}}{{4l}} 10th Harmonic/5th overtone
7.
\frac{{13V}}{{4l}} 13th Harmonic/6th overtone … and so on.
(Only odd harmonic are present)
Harmonics in an Open organ pipe
First Harmonic Or Fundamental note
An open organ pipe is open at both ends. Therefore an antinode is formed at each end. Proceeding as in the case of closed organ pipe, we get
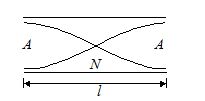
This frequency is called fundamental frequency.
Second Harmonic Or First overtone
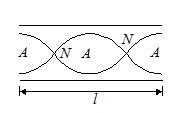
\displaystyle {{f}_{1}}=\frac{V}{\lambda }=\frac{V}{l}
{{f}_{1}}=2f=2 times fundamental frequency =2nd Harmonic.
Third Harmonic Or Second overtone
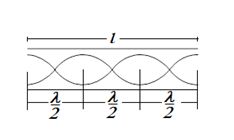
or l=\frac{{6\lambda }}{4}=\frac{{3\lambda }}{2}
\lambda =\frac{{2l}}{3}
{{f}_{2}}=\frac{V}{\lambda }=\frac{V}{{2l/3}}=\frac{{3V}}{{2l}}
=3 times fundamental frequency
Other possible frequencies
1.
\frac{V}{{2l}}\to fundamental frequencies/zero overtone
2.
\frac{{2V}}{{2l}}\to 2nd Harmonic/1st overtone
3.
\frac{{3V}}{{2l}}\to 3rd Harmonic/2nd overtone
4.
\frac{{4V}}{{2l}}\to 4th Harmonic/3rd overtone
5.
\frac{{5V}}{{2l}}\to 5th Harmonic/4th overtone
6.
\frac{{6V}}{{2l}}\to 6th Harmonic/5th overtone
7.
\frac{{7V}}{{2l}}\to 7th Harmonic/6th overtone
8.
\frac{{8V}}{{2l}}\to 8th Harmonic/7th overtone
… and so on.
(All Harmonic (odd & even) are present)
That’s why an open organ pipe is richer over a closed pipe.
=3rd Harmonic
End correction
Actually the antinodes are formed at a distance nearly 0.6 r from the fore end of pipe. This is called end correction, which increases the effective length of the pipe and there increase the wavelength.
Hence, the frequency decreases. As a result of this, wider open pipe has frequency less than a narrow pipe of same length. This effect of diameter is more prominent in an open pipe than in a closed pipe.
Illustration
A tuning fork having frequency of 340 Hz is vibrated just above a cylindrical tube. The height of the tube is 120 cm. Water is slowly poured in. What is the minimum height of water required for resonance? (v = 340 m/s)
Solution:
As the turning fork is in resonance with air column in the pipe closed at one end.
f\,=\,n\frac{v}{{4L}} with n = 1, 3, 5, …
Therefore, the length of air column in the pipe,
L\,=\,\frac{{nv}}{{4f}}\,=\,n\,\frac{{340\times \,100}}{{4\,\times \,340}} = 25n cm with n = 1, 3, 5, …
or L = 25 cm, 75 cm, 125 cm, …
Now, as the tube is 120 cm, the length of air column must be lesser than 120 cm. It can be only 25 cm or 75 cm. Further if h is the height of water filled in the tube.
L + h = 120 cm or h = 10 – L
So h will be minimum when L is maximum, i.e., L = 75 cm
Illustration
Wavelength of two notes in air is (90/175) m and (90/173) m respectively. Each of these notes produce 4 beats per second with a third note of a fixed frequency. Calculate the velocity of sound in air.
Solution:
Given : {{\lambda }_{1}}\,=\,\frac{{90}}{{175}}\,m and {{\lambda }_{2}}\,=\,\frac{{90}}{{173}}
If f1 and f2 are the corresponding frequencies and v is the velocity of sound in air, we have
v=f1l1andv=f2l2
{{f}_{1}}=\,\frac{v}{{{{\lambda }_{1}}}} and f2 = \frac{v}{{{{\lambda }_{2}}}}
Since l1<l2 , we must have f1<f2. If f is the frequency of the third note, then
f1 – f = 4
f1 – f2 = 8
or v\,\left[ {\frac{{175}}{{90}}\,-\,\frac{{173}}{{90}}} \right]= 8
v = 360 m/s
Illustration
A standing wave is maintained in a homogeneous string of cross-sectional areas and density r. It is formed by the superposition of two wave travelling in opposite directions given by the equation
y1 = a sin (wt – kx) and y2 = 2a sin (wt + kx)
Find the total mechanical energy confined between the sections corresponding to the adjacent antinodes.
Solution:
Distance between two adjacent antinodes is l/2 or p/k,
Volume of string between twp adjacent antinodes V = ps/k
E = (V) (u1 + u2)
E = \displaystyle \left( {\frac{\pi }{k}} \right)(s)\left[ {\frac{1}{2}\rho {{a}^{2}}{{\omega }^{2}}+\frac{1}{2}\rho {{{(2a)}}^{2}}{{\omega }^{2}}} \right]=\frac{{5\pi s\rho {{a}^{2}}{{\omega }^{2}}}}{{2k}}
Illustration
The vibrations of a string of length 60 cm fixed at both ends are represented by the equation y = 4 sin \displaystyle \left( {\frac{{\pi x}}{{15}}} \right)\,\cos \left( {96\,\pi \,t} \right)where x and y are in cm and t is in seconds.
(i) What is the maximum displacement of a point at x = 5 cm?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at x = 7.5 cm and at t = 0.25 s?
(iv) Write down the equations of the component waves whose superposition gives the above wave.
Solution:
y = 4 sin(px/15) cos(96pt) can be broken up into
\displaystyle y=2\left[ {\sin \left( {\frac{{\pi \,x\,}}{{15}}+\,96\,\pi \,t} \right)\,+\,\sin \left( {\frac{{\pi \,x}}{{15}}\,-\,96\,\pi \,t} \right)} \right]
Thus, the waves are of the same amplitude and frequency but travelling in opposite directions which, therefore, superimpose to give a standing wave.
(i) At x = 5 cm, the standing wave equation gives
y = 4 sin(5π/15) cos(96πt)
= 4 sin π/3 cos(96πt) = 4 √3/2 cos(96πt)
Maximum displacement = 2√3 cm.
(ii) The nodes are the points permanently at rest. Thus, they are those points for which sin(πx/15) = 0.
i.e. πx/15 = nπ, n = 0, 1, 2, 3, 4, …
or x = 0, 15, 30, 45 and 60 cm
(iii) The particle velocity is equal to
\displaystyle \left( {\frac{{\partial \,y}}{{\partial \,t}}} \right)=4\sin \left( {\frac{{\,\pi \,x}}{{15}}} \right)\,\,(96\,\pi \,)\,(-\sin \,96\pi t)\,
\displaystyle =\,-\,384\,\pi \sin \,\left( {\frac{{\pi \,x}}{{15}}} \right)\,\sin \,(96\,\pi \,t)
At x = 7.5 and t = 0.25 we get
\displaystyle \left( {\frac{{\partial \,y}}{{\partial \,t}}} \right)\,=-\,384\pi \,\sin \,\left( {\frac{{\pi \,x}}{{15}}} \right)\,\sin \,\left( {96\pi t} \right)=-384\pi \,\sin \left( {\frac{\pi }{2}} \right)\sin \left( {24\pi } \right)=0
(iv) The equations of the component waves are
\displaystyle \begin{array}{l}{{y}_{1}}=2\,\sin \,\left( {\frac{{\pi \,x}}{{15}}\,+\,96\,\pi \,t} \right)\\and\,{{y}_{2}}=2\,\sin \,\left( {\frac{{\pi \,x}}{{15}}\,-\,96\,\pi \,t} \right)\end{array}
RESONANCE
Driving an oscillator at a characteristic or natural frequency that gives maximum energy transfer from the driving source to the oscillator.
Resonance Column Method:
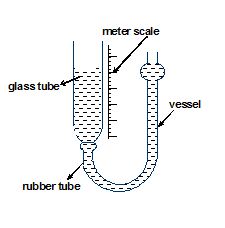
The figure shows schematically the diagram of a simple apparatus used in laboratories to measure the speed of sound in air. The vessel contains water which also goes in the resonance tube through the rubber tube. The level of water in the resonance tube is same as that in the vessel. Thus, by sliding the vessel up and down, one can change the water level in the resonance tube.
The water level in the tube is initially kept high. The tuning fork is vibrated and kept close to the open end, and the loudness of sound coming from the tube is estimated. The vessel is broad down a little to decrease the water level in the resonance tube. The tuning fork is again vibrated, kept close to the open end and the loudness of the sound coming from the tube is estimated.
The length of the air column is read on the scale attached. In this case, the air column vibrates in resonance with the tuning fork. The minimum length of the air column for which the resonance takes place corresponds to the fundamental mode of vibration. A pressure antinode is formed at the water surface (which is the closed end of the air column) and a pressure node is formed near the open end. In fact the node is formed slightly above the open end (end correction) because of the air-pressure from outside.
Thus, for the first resonance the length l1 of the air column in the resonance tube is given by
l1 + d = \frac{\lambda }{4} ….(i)
where d is the end correction.
The length of the air column is increased to a little less than three times of l. The water level is adjusted so that the loudness of the sound coming from the tube becomes maximum again. The length of the air column is noted on the scale. In this second resonance the air column vibrates in the first overtone. There is one node and one antinode in between the ends of the column. The length l2 of the column is given by
l2 + d = 3λ/4 …(ii)
By (i) and (ii),
(l2-l1) = λ/2 or, l = 2(l2-l1).
The frequency of the wave is same as the frequency of the tuning fork. Thus, the speed of sound in the air of the laboratory is
v = vλ = 2(l2-l1)v
Illustration
A resonance air column resonates with a turning fork of frequency 512 Hz at column lengths 16.0 cm, and 49.2 cm. Find the end correction, and the velocity of sound wave in air
Solution:
The resonance air column has one closed end, which is adjustable. Thus, if e is the end correction we have
L1 + e = \frac{\lambda }{4} and L2 + e = \frac{{3\lambda }}{4}
or l = 4(L1 + e) = (L2 + e)
or e = \frac{{{{L}_{2}}-3{{L}_{1}}}}{2}\,=\,\frac{{0.492\,-\,3\,\times \,0.16}}{2}= 0.006 m
Now, v = f l = f × 4 (L1 + e)
= 512 × 4 × (0.16 + 0.006)
= 340 m/s
Illustration
A tuning fork vibrating at frequency 800 Hz produces resonance in a resonance column tube. The upper end is open and the lower end is closed by the water surface which can be varied. Successive resonances are observed at lengths 9.75 cm, 31.25 cm and 52.75 cm. Calculate the speed of sound in air from these data.
Solution:
For the tube open at one end, the resonance frequencies are \frac{{nv}}{{4\ell }}, where n is a positive odd integer. If the tuning fork has a frequency n and l1, l2, l3 are the successive lengths of the tube in resonance with it, we have
\frac{{nv}}{{4{{\ell }_{1}}}}=\nu
\frac{{(n+2)v}}{{4{{\ell }_{2}}}}=\nu
\frac{{(n+4)v}}{{4{{\ell }_{2}}}}=\nu
giving l3-l2 = l2-l1 = \frac{{2v}}{{4\nu }}=\frac{v}{{2\nu }}
By the question, l3-l2 = (52.75 – 31.25)cm = 21.50 cm
and l2-l1 = (31.25 – 9.57) cm = 21.50 cm
Thus, \frac{v}{{2\nu }}=21.50cm
or v = 2n x 21.50 cm = 2 x 800 s-1´ 21.50 cm = 344 m/s
Illustration
The length of a sonometer wire between its fixed ends is 100 cm. Where should two bridges be placed in between the ends so as to divide the wire into 3 segments whose fundamental frequencies are in the ratio 1 : 2 : 3?
Solution:
If L1, L2, L3 be the lengths of the three segments then
L1 + L2 + L3 = 100
If f1, f2 and f3 be the fundamental frequencies of the three segments then
F1 = f
f2 = 2f
f3 = 3f,
since f1 : f2 : f3 = 1 : 2 : 3
The tension remains the same throughout the wire. Hence
f1L1 = f1L2 = f3L3 or, fL1 = 2fL2= 3fL3
or, L1 = 2L2 = 3L3
If L3 = x, L2= \frac{3}{2}\ x, L1 = 3x
L1 + L2 + L3 = 3x + \frac{3}{2}\ x + x = 100 cm or, 11x = 200
L3 = x = \frac{{200}}{{11}} = 18.18 cm
L2 = \frac{3}{2}x\,\,=\frac{{54.54}}{2}=27.27\,\,\mathbf{cm}
L1 = 3x = 54.54 cm
The bridges should be placed in the positions of 54.54 cm from the zero end and 18.18 cm from the other end.
Illustration
A column of air at 51°C and a tuning fork produce 4 beats per second when sounded together. As the temperature of the air column is decreased the number of beats per second tends to decrease and when the temperature is 16°C, the two produce one beat per second. Find the frequency of the tuning fork.
Solution:
Let the velocity of sound in air at 51°C be v1.
Let the corresponding wavelength and frequencies be l1 and f1 in the air column.
When the temperature decreases to 16°C, the corresponding quantities be v2, l2 and n2 respectively.
But the length of the tube remains the same and hence l of stationary waves in both the cases will be the same. Hence
V1 = f1l and V2 = f2l
or \frac{{{{V}_{1}}}}{{{{V}_{2}}}}\ \,\,=\,\ \frac{{{{f}_{1}}}}{{{{f}_{2}}}}
Since Vt = {{V}_{0}}\sqrt{{1\ \,\,+\,\ \frac{{{{t}_{1}}}}{{273}}}}
V1 = {{V}_{0}}\sqrt{{\frac{{273\ +\,\ {{t}_{1}}}}{{273}}}}\ \,\,\,=\,\ {{V}_{0}}\sqrt{{\frac{{273\ +\,\ 51}}{{273}}}} = {{V}_{0}}\sqrt{{\frac{{324}}{{273}}}}
V2 = {{V}_{0}}\sqrt{{\frac{{273\ +\ 16}}{{273}}}}\ \,\,\,\,=\ \,{{V}_{0}}\sqrt{{\frac{{289}}{{273}}}} or, \frac{{{{v}_{1}}}}{{{{v}_{2}}}}\ \,=\,\ \sqrt{{\frac{{324}}{{289}}}}\ =\ \frac{{18}}{{17}}
or \frac{{{{f}_{1}}}}{{{{f}_{2}}}}\ \,=\,\,\ \frac{{18}}{{17}}
If f be the frequency of the tuning fork f1 = f± 4
f2 = f± 1
Since f1>f2, f1 = f + 4
f2 = f + 1
18(f + 1) = 17(f + 4)
18f + 18 = 17f + 68
f = 68 – 18 = 50 Hz
It is also possible n2 = n – 1
18(f – 1) = 17(f + 4)
18 f – 18 = 17 f + 68
f = 68 + 18 = 86 Hz
frequency of the fork = 50 Hz or 86 Hz
Illustration
A wire of length 2 m is kept just taut horizontally between two walls. A mass hanging from its midpoint depresses it by 10 mm. The frequency of transverse vibrations of each segment of the wire is found to be the same as the fundamental frequency of air column in a closed tube of length 5 m. (Velocity of sound in air = 360 m/s). Find the Young’s modulus of the material of the wire if the density of the material of the wire is
7800 kg/m3.
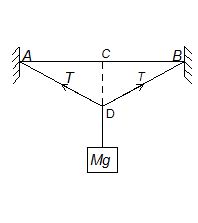
Solution:
AB = 2 m; AC = CB = 1 m = 100 cm; CD = 10 mm = 1 cm
The extension produced in the segment AC of the wire due to the load Mg is given by
DL = AD – AC = \sqrt{{{{{100}}^{2}}\ +\ {{1}^{2}}}}\ -\ 100
= 100\,\ {{\left( {1\,\ +\,\ \frac{1}{{{{{100}}^{2}}}}} \right)}^{{1/2}}}-\ \,100\,\,\,\,\,\,\,\ =\ \,\,100\,\ \left( {1\ \,+\,\ \frac{1}{{2\ \,\times \,\,{{{10}}^{4}}}}} \right)\ -\ 100 = 0.005 cm.
The tension T in the wire is therefore given by T = \frac{{Ya\Delta L}}{L}.
Frequency of the fundamental, f = \frac{1}{{2L}}\,\sqrt{{\frac{T}{m}}}
{{f}^{2}}\,\ =\,\,\ \frac{1}{{4{{L}^{2}}}}\ \cdot \ \frac{T}{m}\ \,\,\,\,\,=\,\ \frac{1}{{4{{L}^{2}}}}\ \cdot \ \frac{{Ya\Delta L}}{L}\ \cdot \ \frac{1}{{a\ \cdot \ D}} (D = density)
or, Y = \frac{{4{{L}^{3}}{{f}^{2}}D}}{{\Delta L}}\ \,=\ \,\frac{{4{{{(1)}}^{3}}({{f}^{2}})\,\,\ (7800)}}{{5\ \,\times \ \,{{{10}}^{{-5}}}}}
The frequency of the wire is the same as the fundamental of a closed tube of 5 m length.
f = \frac{V}{{4L}}\ \,=\,\ \frac{{360}}{{4\ \times \ 5}} = 18 Hz
the Young’s modulus of the material of the wire
Y = \frac{{4\ \times \,\,\ {{{(1)}}^{3}}\ \,\times \,\,\ {{{(18)}}^{2}}\ \times \,\,\ (7800)}}{{5\ \,\times \,\ {{{10}}^{{-5}}}}} = 20.22 x 1010N/m2
Illustration
Two wires of radii r and 2r respectively are welded together end to end. The combination is used as a sonometer wire and is kept under tension T. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the wires such that the joint is a node when stationary vibrations are set up in the wires?
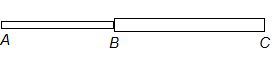
Solution:
ABC is the wire where B is the midpoint of AC. AB is the part with radius r and BC is the part with radius 2r. They are of the same material and hence their volume density is the same. The welded point B will be a node for the stationary wave system formed. Let there be n1 loops of wavelength l1 in AB and n2 loops of wavelength l2 in BC.
Since AB = BC
{{n}_{1}}\frac{{{{\lambda }_{1}}}}{2}\,\,=\,\,{{n}_{2}}\frac{{{{\lambda }_{2}}}}{2}\,\,\,\,\,or,\,\,\,\,\,\,\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,\,=\,\,\frac{{{{n}_{2}}}}{{{{n}_{1}}}} … (i)
Velocity of transverse wave in wire AB:
V1 = \sqrt{{\frac{T}{{\pi {{r}^{2}}D}}}} where T = tension
D = volume density
Velocity of transverse wave in wire BC:
V2 = \sqrt{{\frac{T}{{\pi {{{(2r)}}^{2}}D}}}}
\frac{{{{V}_{1}}}}{{{{V}_{2}}}}= 2 … (ii)
Now \frac{{{{V}_{1}}}}{{{{V}_{2}}}}, where f1 and f2 are frequencies
Since f1 = f2, \frac{{{{V}_{1}}}}{{{{V}_{2}}}}\,\,\,\,=\,\,\,\,\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,\,\,\,=\,\,\,\,\frac{{{{n}_{2}}}}{{{{n}_{1}}}}= 2, using (i) and (ii).
required ratio n1 : n2 = 1 : 2
Illustration
The second overtone of an open pipe has the same frequency as the first overtone of a closed pipe 2 m long. What is the length of the open pipe?
Solution:
Let L0 be the length of the open pipe. The fundamental frequency of the pipe is given by
{{f}_{o}}\ \,\,=\,\,\ \frac{V}{{{{\lambda }_{f}}}}\,\,\ =\,\,\ \frac{V}{{2{{L}_{o}}}}, V = velocity of sound in air
The second overtone of the open pipe has a frequency 3{{f}_{o}}\ \,\,=\,\,\ \frac{{3\,\ \cdot V}}{{2{{L}_{o}}}} Hz
The length of the closed pipe LC = 2 m
The frequency of the fundamental emitted by the closed pipe
{{f}_{c}}\ \,\,=\,\,\ \frac{V}{\lambda }\,\,\ =\,\,\ \frac{V}{{4{{L}_{c}}}}
The first overtone of the closed pipe has a frequency
3{{f}_{c}}\ \,=\ \,\frac{{3V}}{{4{{L}_{c}}}}\,\ =\,\ \frac{{3V}}{{4\ \,\times \,\ 2}}\,\ =\,\ \frac{{3V}}{8}Hz
Now 3f0 = 3fc or, \frac{{3V}}{{4{{L}_{o}}}}\,=\,\ \frac{{3V}}{8}
or 2L0 = 8 or L0 = 4m
Illustration
Two identical steel wires are under tension and are in unison. When the tension in one of the wires is increased by 1 percent 4 beats per second is heard. Find the original frequency of the wires.
Solution:
By unison of the wires, we mean that they have the same frequency of vibration. Since they are identical in linear density and length they must be under the same tension to be in unison.
Let the tension in one wire be increased to {{T}_{1}}\ =\ \,\frac{{101\ T}}{{100}}
where T is the original tension. Let f1 be the new fundamental frequency.
Now \frac{{{{f}_{1}}}}{f}\,\ =\,\ \sqrt{{\frac{{{{T}_{1}}}}{T}}}\,\ =\ \,\sqrt{{\frac{{101}}{{100}}}}
But f1>f and f1 – f = 4
\frac{{f\ \,+\ 4}}{f}\ \,=\ \sqrt{{\frac{{101}}{{100}}}}, 1\ \,+\,\ \frac{4}{f}\,\,=\,\,\ {{\left( {1\ \,+\ \,\,\frac{1}{{100}}} \right)}^{{1/2}}}\,\,\,\,\ \approx \,\,\,\ 1\ \,+\,\,\ \frac{1}{{200}}
\frac{4}{f}\ \,=\,\ \frac{1}{{200}};
f = 800 Hz.
Kundt’s Tube
The apparatus consists of a long glass tube about 5 cm in diameter, fixed horizontally. A metal rod R clamped firmly at the centre is mounted so that its one end carrying a light disc P1 (of cork or card board) projects some distance into the glass tube. The other end of the glass tube is closed with a moveable piston P2. Any desired length of the air or gas can be enclosed in between the two discs P1 and P2. A small amount of dry lycopodium powder or cork dust is spread along base of the entire length of the tube.
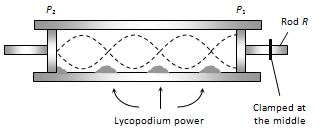
The free end of the metal rod R is rubbed (stroked) along the length with resined cloth. The rod begins to vibrate longitudinally and emits a very high pitched shrill note. These vibrations are impressed upon the air column in the tube through disc P1. Let disc P2 is so adjusted, that the stationary waves are formed in the air (gas) column in the tube. At antinodes powder is set into oscillations vigorously while it remains uneffected at nodes. Heaps of power are formed at nodes.
Let n is the frequency of vibration of the rod then, this is also the frequency of sound wave in the air column in the tube.
For rod : \frac{{{{\lambda }_{{rod}}}}}{2}={{l}_{{rod}}}, For air : \frac{{{{\lambda }_{{air}}}}}{2}={{l}_{{air}}}
where lair is the distance between two heaps of power in the tube (i.e. distance between two nodes). If vair and vrod are velocity of sound waves in the air and rod respectively, then
n=\frac{{{{v}_{{air}}}}}{{{{\lambda }_{{air}}}}}=\frac{{{{v}_{{rod}}}}}{{{{\lambda }_{{rod}}}}}. Therefore \frac{{{{v}_{{air}}}}}{{{{v}_{{rod}}}}}=\frac{{{{\lambda }_{{air}}}}}{{{{\lambda }_{{rod}}}}} =\frac{{{{\lambda }_{{air}}}}}{{{{\lambda }_{{rod}}}}}
Thus knowledge of {{v}_{{rod}}}, determiens {{v}_{{air}}}
Kundt’s tube may be used for
(i) Comparison of velocities of sound in different gases.
(ii) Comparison of velocities of sound in different solids
(iii) Comparison of velocities of sound in a solid and in a gas.
(iv) Comparison of density of two gases.
(v) Determination of g of a gas.
(vi) Determination of velocity of sound in a liquid.
Practice Questions (Basic Level)
Q.1
The standing waves set upon a string are given by
y=4\sin \left( {\frac{{\pi x}}{{12}}} \right)\cos (52\,\pi t)
If x and y are in centimeters and tis in seconds, what is the amplitude of the particle at x=2\,\mathbf{cm}?
(a) 12 cm (b) 4 cm (c) 2 cm (d) 1 cm
Ans. (c)
Q.2
The phase difference between the particles vibrating between two consecutive nodes is
(a) zero
(b) \pi /2
(c) \pi
(d) 2\pi
Ans. (c)
Q.3
A cylindrical tube open at both ends has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air-column is now.
(a) f /2 (b) 3f /4 (c) f (d) 2 f
Ans. (c)
Q.4
The first overtone of an open pipe has the same frequency as the first overtone of a closed pipe of 30 cm long. The length of the open pipe is
(a) 0.3 m (b) 0.4 m (c) 0.5 m (d) 0.6 m
Ans. (b)
Q.5
If fundamental frequency of an closed pipe is {{f}_{o}}. Its fundamental frequency when it is half-filled with water is
(a) {{f}_{o}}
(b) {{f}_{o}}/2
(c) 2{{f}_{o}}
(d) none of these
Ans. (c)
Q.6
The wave produced in a sonometer is
(a) longitudinal
(b) timesavers
(c) transverse stationary
(d) longitudinal stationary
Ans. (c)
Q.7
A tuning fork is vibrating in the 3rd harmonic. Number of antinodes produced in it are
(a) 3 (b) 5 (c) 7 (d) 6
Ans. (a)
Q.8
The third harmonic in an open organ pipe is know as
(a) fundamental frequency
(b) second overtone
(c) third overtone
(d) first overtone
Ans. (b)
Q.9
Two organ pipes are of same size. Hydrogen and oxygen gases are filled in them. Taking the elasticity of two gases to be same. The ratio of their fundamental frequencies will be
(a) 1 : 4 (b) 4 : 1 (c) 8 : 1 (d) 16 : 1
Ans. (b)
Q.10
In an open pipe the harmonics that are missing are
(a) depends upon length of the pipe
(b) none
(c) even
(d) odd
Ans. (b)
Q.11
The separation between a node and an antinodes in the stationery wave y=20\sin (2x)\cos 400\pi t is
(a) \frac{\pi }{2}
(b) \frac{\pi }{4}
(c) \frac{\pi }{6}
(d) \frac{\pi }{8}
Ans. (a)
Practice Questions (JEE Main Level)
Q.1
The equation y=0.15\sin 5x\,\,\cos 300trepresents a stationary wave. The wavelength of this stationary wave will be
(a) 0.628 m (b) 2.512 m (c) 1.256 m (d) zero
Ans. (c)
Q.2
Two harmonic waves are described by
- y1 = 3 sin p (x + 0.6 t) cm
- y2 = 3 sin p (x -6 t) cm
- The three smallest values of x corresponding to antinodes are
(a) \frac{1}{4},\ \,\frac{1}{3},\ \,\frac{1}{2}
(b) \frac{1}{2},\ \,\frac{3}{2},\ \,\frac{5}{2}
(c) \frac{1}{3},\ \,\frac{1}{6},\ \,\frac{1}{9}
(d) 0, \frac{1}{2},\ \,1
Ans. (b)
Q.3
Two wires of same material and radius have the same fundamental frequency. If the ratio of their lengths is 1: 2, the ratio of tension in the two wires is
(a) 1 : 2 (b) 2 : 1 (c) 1 : 4 (d) 4 : 1
Ans. (c)
Q.4
Two wires are kept tight between the same pair of supports. The tensions in the wires are in the ratio 2 : 1. The radii are in the ratio 3 : 1 and the densities are in the ratio 1 : 2. The ratio of their fundamental frequencies are
(a) 1/2 (b) 2/3 (c) 3/4 (d) 4.9
Ans. (b)
Q.5
A tuning fork produces four beats per second with 49 cm and 50 cm lengths of a stretched wire of a sonometer. The frequency of the fork is
(a) 196 Hz (b) 296 Hz (c) 396 Hz (d) 693 Hz
Ans. (c)
Q.6
The tension in a wire is decreased by 19%. The percentage decrease in frequency will be
(a) 10% (b) 19% (c) 0.19% (d) none of these
Ans. (a)
Q.7
An air column in a pipe which is closed at one end will be in resonance with a vibrating tuning fork of frequency 264 Hz if the length of the column in cm is (velocity of sound in air = 330 m/s).
(a) 31.25 (b) 62.50 (c) 90.75 (d) 125
Ans. (a)
Q.8
A tube closed at one end and containing air produces, when excited, the fundamental note of frequency 512 Hz. If the tube is open at both ends, the fundamental frequency that can be excited is (in Hz)
(a) 1024 (b) 512 (c) 256 (d) 128
Ans. (a)
Q.9
An organ pipe P1 closed at one end vibrating in its first overtone and another pipe P2 open at both ends vibrating in its third overtone are in resonance with a given tuning fork. The ratio of the length of P1 to that of P2 is
(a) \frac{8}{3}
(b) \frac{3}{8}
(c) \frac{1}{2}
(d) \frac{1}{3}
Ans. (b)
Q.10
Two organ pipes each closed at one end, give 5 beats per second when emitting their fundamental notes. If their lengths are in the ratio 50 : 51, their fundamental frequencies
(in Hz) are
(a) 250, 255 (b) 255, 260 (c) 260, 265 (d) 265, 270
Ans. (a)
Q.11
A standard tuning fork of frequency f is used to find velocity of sound in air by resonance air column apparatus. The difference between two resonating lengths is 0.5 m. Then the velocity of sound in air is (in m/s)
(a) f
(b) 2 f
(c) \frac{f}{2}
(d) 3 f
Ans. (a)
Q.12
The second overtone of a closed organ pipe {{P}_{1}} and the third overtone of an open pipe {{P}_{2}} are in unison with a tuning fork. The ratio of the length of {{P}_{1}} and {{P}_{2}} will be
(a) 3 : 8 (b) 1 : 3 (c) 8 : 3 (d) 3 : 1
Ans. (a)
Q.13
An open pipe is suddenly closed at one end. As a result the frequency of third harmonic of the closed pipe is found to be higher by 100 Hz. The fundamental frequency of open pipe is
(a) 200 Hz (b) 30 Hz (c) 240 Hz (d) 480 Hz
Ans. (a)
Q.14
A tuning fork of frequency f resonates with a closed organ pipe when the length of the shortest air columns are a and b respectively. The speed of sound in air is
(a) 2f(b+a)
(b) \frac{{f(b-a)}}{2}
(c) 2f(b-a)
(d) \frac{{f(b+a)}}{2}
Ans. (c)
Q.15
Two open pipes of length L are vibrated simultaneously. If length of one of the pipes is reduced by y, then the number of beats heard per second will nearly be (if the velocity of sound is V and y<L)
(a) \frac{{Vy}}{{2L}}
(b) \frac{{2{{L}^{2}}}}{{Vy}}
(c) \frac{{Vy}}{{2{{L}^{2}}}}
(d) \frac{{Vy}}{{{{L}^{2}}}}
Ans. (c)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
