Video Lecture
Theory For Notes Making
Stationary waves
When two waves of same frequency and same amplitude travel in an opposite directions at same speed, their superposition gives rise to a new type of waves called stationary wave or standing wave. Let the two waves of same amplitude, frequency traveling in opposite direction at same speed are
{{y}_{1}}=a\sin (\omega t-kx) and {{y}_{2}}=a\sin (\omega t+kx)
They by the principle of superposition,
y={{y}_{1}}+{{y}_{2}}=(2a\,\cos \,\,kx).\,\sin \omega t{See the video lecture for detailed solution}
{{y}_{1}}=A\,\sin \omega t [where A\,=2\,a\cos kx]
As this equation satisfies the wave equation \frac{{{{d}^{2}}y}}{{d{{x}^{2}}}}=\frac{{-1}}{{{{v}^{2}}}}\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}}, so it represents a wave. However as it is not of the form of f(ax\pm bt). The wave is not traveling and so it is called standing wave.
The amplitude of the wave =A=2\,a\cos kxis NOT constant but varies periodically with position.
The points for which amplitude is minimum are called nodes and for these \cos \,kx=0
kx=\pm \frac{\pi }{2},\,\,\pm \frac{{3\pi }}{2},\,\,\pm \frac{{5\pi }}{2},\,\,\pm \frac{{7\pi }}{2}……
or x=\pm \frac{\lambda }{4},\,\,\pm \frac{{3\lambda }}{4},\,\,\pm \frac{{5\lambda }}{4},\,……
This shows that all the nodes are equally spaced and the spacing between two adjacent nodes is \lambda /2 with {{A}_{{\min }}}=0. Nodes are permanently at rest.
The points for which amplitude is maximum are called antinodes. For these \cos \,kx=\pm 1 i.e., kx=0,\,\,\,\,\pm \pi ,\,\,\,\,\mp 2\pi ,\,\,\,\,\pm 3\pi …..
x=0,\,\,\pm \frac{\lambda }{2},\,\,\frac{{2\lambda }}{2},\,\,\frac{{3\lambda }}{2}…..
Like nodes anitinodes are also equispaced with space (\lambda /2) and {{(A)}_{{\max }}}=\pm \,\,2A. Further node and antinode are separated with spacing \lambda /4.
Reflection and Refraction/Transmission of Wave
Effect on different variables : In case of reflection, because medium is same and hence, speed, frequency (w) and wavelength l (or k) do not changes.
On the other hand in case of transmitted wave since medium changes and hence speed, wavelength (or k) changes but frequency (w) remains the same.
Boundary conditions : Reflection of a wave pulse from some boundary depends on the nature of the boundary.
(a)
Waves on reflection from a fixed end undergo a phase change of 180°
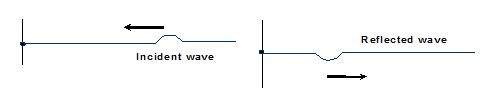
(b)
A wave reflected from a free end returns without a change in phase.

(c)
In case of a pressure wave, there is no phase change when reflected from a denser medium or fixed end and there is phase change by p when reflected from rarer medium.
(d)
Wave in a combination of string
(i) Wave goes from rarer to denser medium
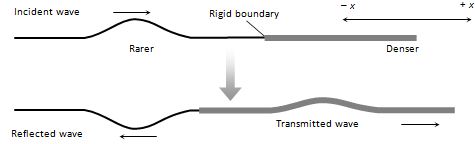
Incident wave {{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)
Reflected wave {{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+\pi ] =-\,a\sin \,(\omega \,t+{{k}_{1}}x)
Transmitted wave {{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)
(ii) Wave goes from denser to rarer medium
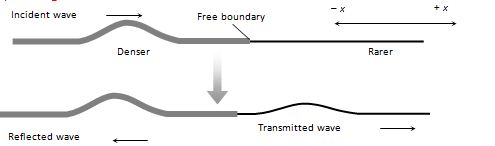
Incident wave {{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)
Reflected wave {{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+0] =\,a\sin \,(\omega \,t+{{k}_{1}}x)
Transmitted wave {{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)
(iii) Ratio of amplitudes : It is given as follows
\frac{{{{a}_{r}}}}{{{{a}_{i}}}}=\frac{{{{k}_{1}}-{{k}_{2}}}}{{{{k}_{1}}+{{k}_{2}}}}=\frac{{{{v}_{2}}-{{v}_{1}}}}{{{{v}_{2}}+{{v}_{1}}}} and \frac{{{{a}_{t}}}}{{{{a}_{i}}}}=\frac{{2{{k}_{1}}}}{{{{k}_{1}}+{{k}_{2}}}}=\frac{{2{{v}_{2}}}}{{{{v}_{1}}+{{v}_{2}}}}
Harmonics in a Stretched string
When a string under tension is set into vibrations, then transverse harmonic wave propagate along its length. When the length is finite, then reflected waves also exist. The incident and reflected waves will superimpose to produce transverse stationary waves in the string.
First Harmonic Or Fundamental note
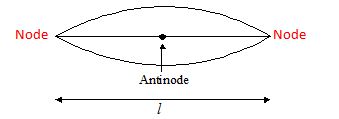
Let length of string be l and N to AN=\lambda /4 and AN to N=\lambda /4
N to N=\frac{\lambda }{4}+\frac{\lambda }{4}=\frac{{2\lambda }}{4}=\frac{\lambda }{2}
Equating \frac{\lambda }{2}=l,\,\,\,\,\lambda =2l
Now, V=f\lambda ,\,\,\,\,f=\frac{V}{\lambda }=\frac{V}{{2l}}
But velocity in case of stretched string is given by V=\sqrt{{\frac{T}{m}}}
Where T= tension in string.
m=mass per unit length.
= linear mass density.
f=\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}
This is the minimum possible frequency that we can have. This frequency is called as fundamental frequency.
Second Harmonic Or First overtone
At the fixed end, node is always formed because that ends cannot vibrate at all.
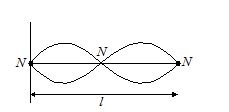
Distance in terms of wavelength =4\cdot \,\frac{\lambda }{4}=\lambda and geometrical length =l. Therefore
\lambda =l,\,\,V=f\lambda ,\,\,\,\,\,\,{{f}_{1}}=\frac{V}{l}=\frac{{2V}}{{2l}}=2\cdot \left[ {\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}} \right]=2 [Fundamental frequency]
Since it is twice of times the fundamental frequency, so this frequency is called as 2nd (second) harmonic.
Third Harmonic Or Second overtone
Distance in term of wavelength =\frac{{6\lambda }}{4}=\frac{{3\lambda }}{2}
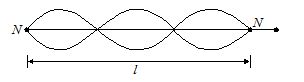
Geometrical length =l
\frac{{3\lambda }}{2}=l\,\,\,\,\,\,\,\,\,\,\,\lambda =\frac{{2l}}{3} {{f}_{2}}=\frac{V}{\lambda }=\frac{V}{{\frac{{2\lambda }}{3}}}=\frac{{3V}}{{2l}}=3.\frac{1}{{2l}}\sqrt{{\frac{T}{m}}} =3 [Fundamental frequency]
Since this frequency {{f}_{2}} is 3 times the fundamental frequency. Therefore this is called as 3rd [third] harmonic.
If we continue in the same way, we get the series of frequencies which is
\frac{1}{{2l}}\sqrt{{\frac{T}{m}}}→ fundamental frequency → zero overtone.
\frac{2}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,2ndHarmonic \xrightarrow{{}}\,\,1st\,\,overtone
\frac{3}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,3rd Harmonic \xrightarrow{{}}\,\,2nd\,\, overtone
\frac{4}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,4th Harmonic \xrightarrow{{}}\,\,3rd\, overtone
\frac{5}{{2l}}\sqrt{{\frac{T}{m}}}\,\,\xrightarrow{{}}\,\,5th Harmonic \xrightarrow{{}}\,\,4th\, overtone
All odd and even harmonics are present.
If it vibrates in p loops f=\frac{p}{{2l}}\sqrt{{\frac{T}{m}}}
Law’s of vibration of stretched string f=\frac{p}{{2l}}\sqrt{{\frac{T}{{(Al)d/l}}}}=\frac{p}{{2l}}\sqrt{{\frac{{Tl}}{{\frac{{\pi {{D}^{2}}}}{4}.l.d}}}}=\frac{p}{{2l}}\sqrt{{\frac{{4Tl}}{{\pi {{D}^{2}}\,l.d}}}}
1.
law of length f\propto \,\,\frac{1}{l}
2.
law of tension f\propto \,\,\sqrt{T}
3.
law of diameter f\propto \,\,\frac{1}{D}
4.
law of density f\propto \,\,\frac{1}{{\sqrt{d}}}
Standing waves in closed organ pipe
Organ pipes are the numerical instruments, which are used for producing numerical sound by blowing air into the pipe.
Longitudinal standing waves are formed in account of superposition of incident and reflected longitudinal waves.
Organ pipe are of two types:
(i)
Closed organ pipe
(ii)
Open organ pipe
Harmonics in a Closed organ pipe
First Harmonic Or Fundamental note
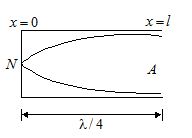
\mathbf{V}=f\lambda ,\,\,\,f=\frac{V}{{4l}}
f=\frac{V}{{4l}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\because \,\,\,\,\,\left( {\frac{\lambda }{4}=l} \right)
This is the minimum possible frequency that we would arrange and it is called as fundamental frequency.
Third Harmonic Or First overtone
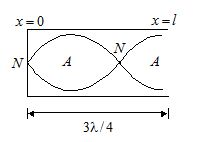
\frac{{3\lambda }}{4}=l), \lambda =\frac{{4l}}{3}
{{f}_{1}}=\frac{{3V}}{{4l}} , {{f}_{2}}=\frac{V}{{4l/3}}
This frequency {{f}_{1}} is 3 times the fundamental frequency. Hence called as 3rd Harmonic
Fifth Harmonic Or Second overtone
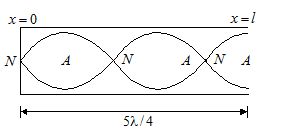
\frac{{5\lambda }}{4}=l
\lambda =\frac{{4l}}{5} {{f}_{2}}=\frac{\mathbf{V}}{{4l/5}}=\left( {\frac{{5\mathbf{V}}}{{4l}}} \right)
This frequency {{f}_{2}} is 5 times the fundamental frequency. Hence called as 5th Harmonic.
In Similar way
We can arrange the further frequencies.
1.
\frac{V}{{4l}} fundamental frequency/zero overtone
2.
\frac{{3V}}{{4l}} 3rd Harmonic/1st overtone
3.
\frac{{5V}}{{4l}} 5th Harmonic/2nd overtone
4.
\frac{{7V}}{{4l}} 7th Harmonic/3rd overtone
5.
\frac{{9V}}{{4l}} 9th Harmonic/4th overtone
6.
\frac{{11V}}{{4l}} 10th Harmonic/5th overtone
7.
\frac{{13V}}{{4l}} 13th Harmonic/6th overtone … and so on.
(Only odd harmonic are present)
Harmonics in an Open organ pipe
First Harmonic Or Fundamental note
An open organ pipe is open at both ends. Therefore an antinode is formed at each end. Proceeding as in the case of closed organ pipe, we get
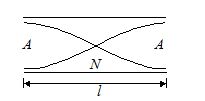
This frequency is called fundamental frequency.
Second Harmonic Or First overtone
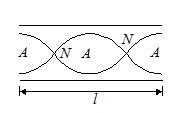
\displaystyle {{f}_{1}}=\frac{V}{\lambda }=\frac{V}{l}
{{f}_{1}}=2f=2 times fundamental frequency =2nd Harmonic.
Third Harmonic Or Second overtone
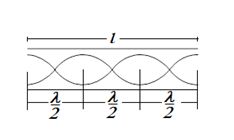
or l=\frac{{6\lambda }}{4}=\frac{{3\lambda }}{2}
\lambda =\frac{{2l}}{3}
{{f}_{2}}=\frac{V}{\lambda }=\frac{V}{{2l/3}}=\frac{{3V}}{{2l}}
=3 times fundamental frequency
Other possible frequencies
1.
\frac{V}{{2l}}\to fundamental frequencies/zero overtone
2.
\frac{{2V}}{{2l}}\to 2nd Harmonic/1st overtone
3.
\frac{{3V}}{{2l}}\to 3rd Harmonic/2nd overtone
4.
\frac{{4V}}{{2l}}\to 4th Harmonic/3rd overtone
5.
\frac{{5V}}{{2l}}\to 5th Harmonic/4th overtone
6.
\frac{{6V}}{{2l}}\to 6th Harmonic/5th overtone
7.
\frac{{7V}}{{2l}}\to 7th Harmonic/6th overtone
8.
\frac{{8V}}{{2l}}\to 8th Harmonic/7th overtone
… and so on.
(All Harmonic (odd & even) are present)
That’s why an open organ pipe is richer over a closed pipe.
=3rd Harmonic
End correction
Actually the antinodes are formed at a distance nearly 0.6 r from the fore end of pipe. This is called end correction, which increases the effective length of the pipe and there increase the wavelength.
Hence, the frequency decreases. As a result of this, wider open pipe has frequency less than a narrow pipe of same length. This effect of diameter is more prominent in an open pipe than in a closed pipe.
Illustration
A tuning fork having frequency of 340 Hz is vibrated just above a cylindrical tube. The height of the tube is 120 cm. Water is slowly poured in. What is the minimum height of water required for resonance? (v = 340 m/s)
Solution:
As the turning fork is in resonance with air column in the pipe closed at one end.
f\,=\,n\frac{v}{{4L}} with n = 1, 3, 5, …
Therefore, the length of air column in the pipe,
L\,=\,\frac{{nv}}{{4f}}\,=\,n\,\frac{{340\times \,100}}{{4\,\times \,340}} = 25n cm with n = 1, 3, 5, …
or L = 25 cm, 75 cm, 125 cm, …
Now, as the tube is 120 cm, the length of air column must be lesser than 120 cm. It can be only 25 cm or 75 cm. Further if h is the height of water filled in the tube.
L + h = 120 cm or h = 10 – L
So h will be minimum when L is maximum, i.e., L = 75 cm
Illustration
The vibrations of a string of length 60 cm fixed at both ends are represented by the equation y = 4 sin \displaystyle \left( {\frac{{\pi x}}{{15}}} \right)\,\cos \left( {96\,\pi \,t} \right)where x and y are in cm and t is in seconds.
(i) What is the maximum displacement of a point at x = 5 cm?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at x = 7.5 cm and at t = 0.25 s?
(iv) Write down the equations of the component waves whose superposition gives the above wave.
Solution:
y = 4 sin(px/15) cos(96pt) can be broken up into
\displaystyle y=2\left[ {\sin \left( {\frac{{\pi \,x\,}}{{15}}+\,96\,\pi \,t} \right)\,+\,\sin \left( {\frac{{\pi \,x}}{{15}}\,-\,96\,\pi \,t} \right)} \right]
Thus, the waves are of the same amplitude and frequency but travelling in opposite directions which, therefore, superimpose to give a standing wave.
(i) At x = 5 cm, the standing wave equation gives
y = 4 sin(5π/15) cos(96πt)
= 4 sin π/3 cos(96πt) = 4 √3/2 cos(96πt)
Maximum displacement = 2√3 cm.
(ii) The nodes are the points permanently at rest. Thus, they are those points for which sin(πx/15) = 0.
i.e. πx/15 = nπ, n = 0, 1, 2, 3, 4, …
or x = 0, 15, 30, 45 and 60 cm
(iii) The particle velocity is equal to
\displaystyle \left( {\frac{{\partial \,y}}{{\partial \,t}}} \right)=4\sin \left( {\frac{{\,\pi \,x}}{{15}}} \right)\,\,(96\,\pi \,)\,(-\sin \,96\pi t)\,
\displaystyle =\,-\,384\,\pi \sin \,\left( {\frac{{\pi \,x}}{{15}}} \right)\,\sin \,(96\,\pi \,t)
At x = 7.5 and t = 0.25 we get
\displaystyle \left( {\frac{{\partial \,y}}{{\partial \,t}}} \right)\,=-\,384\pi \,\sin \,\left( {\frac{{\pi \,x}}{{15}}} \right)\,\sin \,\left( {96\pi t} \right)=-384\pi \,\sin \left( {\frac{\pi }{2}} \right)\sin \left( {24\pi } \right)=0
(iv) The equations of the component waves are
\displaystyle \begin{array}{l}{{y}_{1}}=2\,\sin \,\left( {\frac{{\pi \,x}}{{15}}\,+\,96\,\pi \,t} \right)\\and\,{{y}_{2}}=2\,\sin \,\left( {\frac{{\pi \,x}}{{15}}\,-\,96\,\pi \,t} \right)\end{array}
Illustration
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of sound in steel?
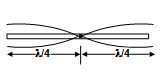
Solution:
Here, \displaystyle \frac{\lambda }{4}+\frac{\lambda }{4}=100\,\,cm=1\,\,m
\displaystyle \frac{\lambda }{2}=1\,\,m
λ = 2 m
Here, n = 2.53 kHz = 2530 Hz.
Speed of sound in steel, v = nl = 2530 Hz x 2 m
= 5060 m/s
Illustration
Two wires of radii r and 2r respectively are welded together end to end. The combination is used as a sonometer wire and is kept under tension T. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the wires such that the joint is a node when stationary vibrations are set up in the wires?
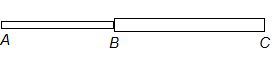
Solution:
ABC is the wire where B is the midpoint of AC. AB is the part with radius r and BC is the part with radius 2r. They are of the same material and hence their volume density is the same. The welded point B will be a node for the stationary wave system formed. Let there be n1 loops of wavelength l1 in AB and n2 loops of wavelength l2 in BC.
Since AB = BC
{{n}_{1}}\frac{{{{\lambda }_{1}}}}{2}\,\,=\,\,{{n}_{2}}\frac{{{{\lambda }_{2}}}}{2}\,\,\,\,\,or,\,\,\,\,\,\,\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,\,=\,\,\frac{{{{n}_{2}}}}{{{{n}_{1}}}} … (i)
Velocity of transverse wave in wire AB:
V1 = \sqrt{{\frac{T}{{\pi {{r}^{2}}D}}}} where T = tension
D = volume density
Velocity of transverse wave in wire BC:
V2 = \sqrt{{\frac{T}{{\pi {{{(2r)}}^{2}}D}}}}
\frac{{{{V}_{1}}}}{{{{V}_{2}}}}= 2 … (ii)
Now \frac{{{{V}_{1}}}}{{{{V}_{2}}}}, where f1 and f2 are frequencies
Since f1 = f2, \frac{{{{V}_{1}}}}{{{{V}_{2}}}}\,\,\,\,=\,\,\,\,\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}}\,\,\,\,=\,\,\,\,\frac{{{{n}_{2}}}}{{{{n}_{1}}}}= 2, using (i) and (ii).
required ratio n1 : n2 = 1 : 2
Illustration
The second overtone of an open pipe has the same frequency as the first overtone of a closed pipe 2 m long. What is the length of the open pipe?
Solution:
Let L0 be the length of the open pipe. The fundamental frequency of the pipe is given by
{{f}_{o}}\ \,\,=\,\,\ \frac{V}{{{{\lambda }_{f}}}}\,\,\ =\,\,\ \frac{V}{{2{{L}_{o}}}}, V = velocity of sound in air
The second overtone of the open pipe has a frequency 3{{f}_{o}}\ \,\,=\,\,\ \frac{{3\,\ \cdot V}}{{2{{L}_{o}}}} Hz
The length of the closed pipe LC = 2 m
The frequency of the fundamental emitted by the closed pipe
{{f}_{c}}\ \,\,=\,\,\ \frac{V}{\lambda }\,\,\ =\,\,\ \frac{V}{{4{{L}_{c}}}}
The first overtone of the closed pipe has a frequency
3{{f}_{c}}\ \,=\ \,\frac{{3V}}{{4{{L}_{c}}}}\,\ =\,\ \frac{{3V}}{{4\ \,\times \,\ 2}}\,\ =\,\ \frac{{3V}}{8}Hz
Now 3f0 = 3fc or, \frac{{3V}}{{4{{L}_{o}}}}\,=\,\ \frac{{3V}}{8}
or 2L0 = 8 or L0 = 4m
Illustration
Two identical steel wires are under tension and are in unison. When the tension in one of the wires is increased by 1 percent 4 beats per second is heard. Find the original frequency of the wires.
Solution:
By unison of the wires, we mean that they have the same frequency of vibration. Since they are identical in linear density and length they must be under the same tension to be in unison.
Let the tension in one wire be increased to {{T}_{1}}\ =\ \,\frac{{101\ T}}{{100}}
where T is the original tension. Let f1 be the new fundamental frequency.
Now \frac{{{{f}_{1}}}}{f}\,\ =\,\ \sqrt{{\frac{{{{T}_{1}}}}{T}}}\,\ =\ \,\sqrt{{\frac{{101}}{{100}}}}
But f1>f and f1 – f = 4
\frac{{f\ \,+\ 4}}{f}\ \,=\ \sqrt{{\frac{{101}}{{100}}}}, 1\ \,+\,\ \frac{4}{f}\,\,=\,\,\ {{\left( {1\ \,+\ \,\,\frac{1}{{100}}} \right)}^{{1/2}}}\,\,\,\,\ \approx \,\,\,\ 1\ \,+\,\,\ \frac{1}{{200}}
\frac{4}{f}\ \,=\,\ \frac{1}{{200}};
f = 800 Hz.
Objective Assignment
Q.1
The standing waves set upon a string are given by
y=4\sin \left( {\frac{{\pi x}}{{12}}} \right)\cos (52\,\pi t)
If x and y are in centimeters and tis in seconds, what is the amplitude of the particle at x=2\,\mathbf{cm}?
(a) 12 cm (b) 4 cm (c) 2 cm (d) 1 cm
Ans. (c)
Q.2
The phase difference between the particles vibrating between two consecutive nodes is
(a) zero
(b) \pi /2
(c) \pi
(d) 2\pi
Ans. (c)
Q.3
A cylindrical tube open at both ends has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air-column is now.
(a) f /2 (b) 3f /4 (c) f (d) 2 f
Ans. (c)
Q.4
The first overtone of an open pipe has the same frequency as the first overtone of a closed pipe of 30 cm long. The length of the open pipe is
(a) 0.3 m (b) 0.4 m (c) 0.5 m (d) 0.6 m
Ans. (b)
Q.5
If fundamental frequency of an closed pipe is {{f}_{o}}. Its fundamental frequency when it is half-filled with water is
(a) {{f}_{o}}
(b) {{f}_{o}}/2
(c) 2{{f}_{o}}
(d) none of these
Ans. (c)
Q.6
The wave produced in a sonometer is
(a) longitudinal
(b) timesavers
(c) transverse stationary
(d) longitudinal stationary
Ans. (c)
Q.7
A tuning fork is vibrating in the 3rd harmonic. Number of antinodes produced in it are
(a) 3 (b) 5 (c) 7 (d) 6
Ans. (a)
Q.8
The third harmonic in an open organ pipe is know as
(a) fundamental frequency
(b) second overtone
(c) third overtone
(d) first overtone
Ans. (b)
Q.9
Two organ pipes are of same size. Hydrogen and oxygen gases are filled in them. Taking the elasticity of two gases to be same. The ratio of their fundamental frequencies will be
(a) 1 : 4 (b) 4 : 1 (c) 8 : 1 (d) 16 : 1
Ans. (b)
Q.10
In an open pipe the harmonics that are missing are
(a) depends upon length of the pipe
(b) none
(c) even
(d) odd
Ans. (b)
Q.11
The separation between a node and an antinodes in the stationery wave y=20\sin (2x)\cos 400\pi t is
(a) \frac{\pi }{2}
(b) \frac{\pi }{4}
(c) \frac{\pi }{6}
(d) \frac{\pi }{8}
Ans. (a)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
