Video Lecture
Theory For Making Notes
Rigid body rotation about a Moving axis board
Here we analysis the dynamics of rotational motion to some cases in which the axis of rotation a moves. When the happens, the motion of the body is combined translation and rotation. In such situation we always consider that “Every possible motion of a rigid body can be represented as a combination of translational motion of the centre of mass and rotation about an axis through the centre of mass”. This is true even when the centre of mass accelerates, so that it is not at rest in any inertial frame. From example when a bowler throws a ball with spin, in air ball follows a parabolic trajectory as it were a point mass and during this motion the ball is also rotating about its centre of mass. The translation of the centre of mass and the rotation about the centre of mass can eb treated independently.
Energy of a body in simultaneous translation and rotational motion
When a body has both translational rotational motion, its total energy can be written as the sum of the two respective kinetic energies. For example, if a body of mass M is rotating about a given axis with an angular speed ω and its moment of inertia about the axis is I and simultaneously the axis moves with a linear velocity v, its total energy can be written as
\displaystyle K=K{{E}_{{\text{tran}}}}+K{{E}_{{\text{rot}}}}
\displaystyle K=\frac{1}{2}M{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}}
An important case of combined translation and rotation is rolling motion, such as the motion of the wheel shown in figure. The wheel is symmetrical so its centre of mass is at its geometric centre. The rolling motion of this wheel can be analyzed by taking translational and rotational motion separately.
When centre of mass of a wheel moves translationally with a speed vcm along with the body in same direction and when it rotates with an angular speed w about its centre, all points on it revolve in different circular paths with the same angular speed w and the points will have linear tangential speed rw if the point is at a distance r from the axis of rotation. If the angular speed of rotation is such that the linear tangential speed of the points on the periphery of the wheel is equal to the translational speed of wheel, then on combining the two motions, the resultant motion is known as pure rolling motion or rolling motion without slipping. This is shown in figure.
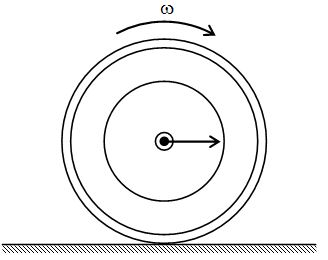
In this situation the point on the wheel that contact the surface must be instantaneously at rest so that it does not slip. Hence the velocity rw of the point of contact relative to the centre of mass must have same magnitude but opposite direction as the centre of mass velocity vcm. Thus for pure rolling.
Vcm = rω
The above relation is the condition of pure rolling. Figure shows the velocity of a point on the wheel is the vector sum of the velocity of the centre of mass and the velocity of the point relative to the centre of mass. Thus while point O, the point of contact, is instantaneously at rest, point 2 at the top of the wheel is moving forward twice as fast as the centre of mass, and point 1 and 3 at the sides have velocities at 45° to the horizontal moving at speed √2 times the centre of mass.
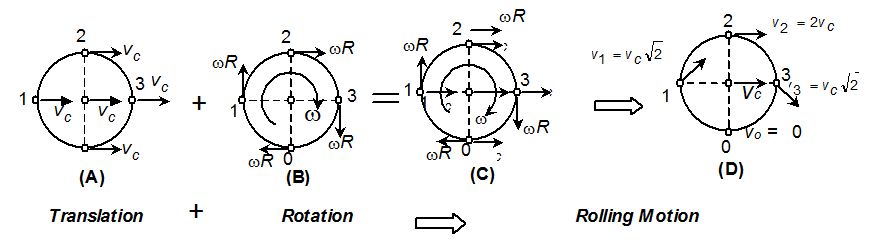
At any instant we can think of the wheel as rotating about an instantaneous axis of rotation that passes through the point of contact with the ground. The angular velocity w is the same for the axis as for an axis through the centre of mass, an observer at the rim watching the centre of mass spin around him. If we think of motion of rolling wheel in this way, the kinetic energy of the wheel is \displaystyle \frac{1}{2}{{I}_{0}}{{\omega }^{2}} where I0 is the moment of inertia of the wheel about an axis through point O. Using parallel axis theorem I0 = Icm + MR2, where Icm is the moment of inertia of the wheel with respect to an axis through the centre of mass. Thus the kinetic energy in this reference is
\displaystyle K=\frac{1}{2}{{I}_{0}}{{\omega }^{2}}=\frac{1}{2}{{I}_{{cm}}}{{\omega }^{2}}+\frac{1}{2}M{{R}^{2}}{{\omega }^{2}}
or = \displaystyle \frac{1}{2}{{I}_{{cm}}}{{\omega }^{2}}+\frac{1}{2}Mv_{{cm}}^{2} \displaystyle \because {{v}_{{cm}}}=R\omega
It is same as that given by equation \displaystyle K=\frac{1}{2}M{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}}. It shows that while solving problems of rolling motion we can solve using both the methods i.e. one by considering the axis of rotation at the centre or in a reference frame attached to the centre of mass of the rolling body and the same problem can also be solved by taking reference frame attached to the instantaneous axis of rotation.
The ratio of rotational kinetic energy and translational kinetic energy
\frac{{\text{Rotational kinetic energy}}}{{\text{Translational kinetic energy}}}=\frac{{\frac{1}{2}I{{\omega }^{2}}}}{{\frac{1}{2}M{{v}^{2}}}} =\frac{{M{{K}^{2}}{{\omega }^{2}}}}{{M{{R}^{2}}{{\omega }^{2}}}}=\frac{{{{K}^{2}}}}{{{{R}^{2}}}}
The ratio of rotation kinetic energy and total energy
\frac{{\text{Rotational kinetic energy}}}{{\text{Total energy}}}=\frac{{\frac{1}{2}I{{\omega }^{2}}}}{{\frac{1}{2}M{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}}}} =\frac{{M{{K}^{2}}{{\omega }^{2}}}}{{M{{R}^{2}}{{\omega }^{2}}+M{{K}^{2}}{{\omega }^{2}}}}= {\frac{{{{K}^{2}}}}{{{{R}^{2}}+{{K}^{2}}}}}
The ratio of translational kinetic energy and total energy
\frac{{\text{Translational kinetic energy}}}{{\text{Total energy}}}=\frac{{\frac{1}{2}M{{v}^{2}}}}{{\frac{1}{2}M{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}}}} =\frac{{M{{v}^{2}}}}{{M{{v}^{2}}+M{{K}^{2}}\frac{{{{v}^{2}}}}{{{{R}^{2}}}}}}=\frac{1}{{1+\frac{{{{K}^{2}}}}{{{{R}^{2}}}}}}={\frac{{{{R}^{2}}}}{{{{R}^{2}}+{{K}^{2}}}}}
When the pure rolling takes place on a rough surface the static friction acts between the body and the surface. where as in case of rolling with slipping the kinetic friction acts.
Rolling | Rolling with Slipping | ||
(i) | Value of friction force (f) | 0 ≤fstatic≤fmax | fkinetic = fmax |
(ii) | W.D. by friction force(f) | Wf = 0 | Wf ≠ 0 |
Acceleration and the frictional force acting on a rigid body of radius of gyration k and radius R rolls (without slipping) down a plane inclined at an angle with horizontal :
When the body is placed on the inclined plane, it tries to slip down and hence a static friction f acts upwards. This friction provides a torque which causes the body to rotate. Let a be the linear acceleration of centre of mass and be the angular acceleration of the body.
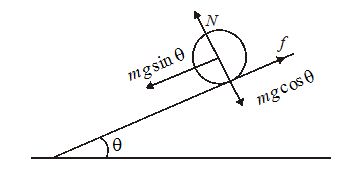
From free body diagram :
for linear motion parallel to the plane apply Fnet = m.a
\displaystyle mg\sin \theta -f=ma———-(i)
for rotation around the axis through centre of mass apply \displaystyle \tau =I\alpha
\displaystyle \Rightarrow fR={{I}_{{cm}}}\alpha —–(ii) here Icm is moment of inertia about the center of mass and can be written as mk2.
wherek is radius of gyration
note that mg is acting at the center therefore its torque about the center is zero
As there is no slipping, the point of contact of the body with plane is instantaneously at rest.
hence \displaystyle v=R\omega
and \displaystyle a=R\alpha ———(iii)
Solving the three equations for a and f :
we get
\displaystyle a=\frac{{g\sin \theta }}{{1+\frac{{{{I}_{{cm}}}^{2}}}{{m{{R}^{2}}}}}} Or \displaystyle a=\frac{{g\sin \theta }}{{1+\frac{{{{k}^{2}}}}{{{{R}^{2}}}}}} and \displaystyle f=\frac{{mg\sin \theta }}{{1+\frac{{{{R}^{2}}}}{{{{k}^{2}}}}}}
Condition for pure rolling (rolling without slipping)
To avoid slipping, the friction must be static in nature, whose maximum value is
\displaystyle f\le {{\mu }_{s}}N
\displaystyle \frac{{g\sin \theta }}{{1+{{R}^{2}}/{{K}^{2}}}}\le {{\mu }_{s}}mg\cos \theta
\displaystyle {{\mu }_{s}}\ge \frac{{\tan \theta }}{{1+\frac{{{{R}^{2}}}}{{{{k}^{2}}}}}}
Time taken by the rolling body to reach the bottom of the inclined plane
Using S=ut+\frac{1}{2}a{{t}^{2}}, we get
l=\frac{1}{2}a{{t}^{2}}or t=\sqrt{{\frac{{2l}}{a}}}or t=\sqrt{{\frac{{2l\left[ {1+\frac{{{{K}^{2}}}}{{{{R}^{2}}}}} \right]}}{{g\sin \theta }}}}
This is the condition of μsfor rolling without slipping.
Important Points To Remember
1.
For solid sphere, \displaystyle {{I}_{{cm}}}=\frac{2}{5}m{{R}^{2}}, \displaystyle a=\frac{5}{7}g\sin \theta
2.
For hollow sphere, \displaystyle {{I}_{{cm}}}=\frac{2}{3}m{{R}^{2}}, \displaystyle a=\frac{3}{5}g\sin \theta
3.
For disc or solid cylinder, \displaystyle {{I}_{{cm}}}=\frac{1}{2}m{{R}^{2}}, \displaystyle a=\frac{2}{3}g\sin \theta
4.
For ring or hollow cylinder, \displaystyle {{I}_{{cm}}}=m{{R}^{2}}, \displaystyle a=\frac{1}{2}g\sin \theta
Note: We can see that acceleration is independent of mass and radius of the body but it depends on the geometrical shape of the body and inclination of plane.
5.
Body | k | ETranslation | ERotation | ETotal | Ratio of ETranslation& ETotal | Ratio of ERotation& ETotal |
Ring or Hollow Cylinder | R | \displaystyle \frac{1}{2}Mv2 | \displaystyle \frac{1}{2}Mv2 | Mv2 | \displaystyle \frac{1}{2} | \displaystyle \frac{1}{2} |
Disc or Solid Cylinder | \displaystyle \frac{R}{{\sqrt{2}}} | \displaystyle \frac{1}{2}Mv2 | \displaystyle \frac{1}{4}Mv2 | \displaystyle \frac{3}{4}Mv2 | \displaystyle \frac{2}{3} | \displaystyle \frac{1}{3} |
Solid Sphere | \displaystyle \sqrt{{\frac{2}{5}}}R | \displaystyle \frac{1}{2}Mv2 | \displaystyle \frac{1}{5}Mv2 | \displaystyle \frac{7}{10}Mv2 | \displaystyle \frac{5}{7} | \displaystyle \frac{2}{7} |
Spherical Shell | \displaystyle \sqrt{{\frac{2}{3}}}R | \displaystyle \frac{1}{2}Mv2 | \displaystyle \frac{1}{3}Mv2 | \displaystyle \frac{5}{6}Mv2 | \displaystyle \frac{3}{5} | \displaystyle \frac{2}{5} |
Illustration
A circular disc rolls down an inclined plane with a height ‘h’ from horizontal surface. Find
(a) Direction of friction force on disc
(b) What will be the fraction of the total energy associated with its translational energy?
(c) Is there any work done by friction force (yes/no)?
Answers
(a) Upward along inclined surface.
(b) \displaystyle \frac{{{{E}_{{Translational}}}}}{{{{E}_{{Total}}}}}=\frac{{\frac{1}{2}m{{v}^{2}}}}{{\frac{1}{2}m{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}}}}=\frac{2}{3}.
(c) In case of rolling, there is no slipping so work done by the friction force is zero.
Illustration
A sphere of radius r and mass m is released from rest from the top of an inclined plane from a height h. Find its velocity at the bottom of the plane. If (a) plane is smooth, (b) plane is sufficiently rough
(a) In the case of switch plane the sphere slides down without rolling and hence applying conservation of energy we get
\displaystyle mgh\,\,=\,\,\frac{1}{2}\,\,m{{v}^{2}}\,\,\Rightarrow \,\,\,\,\,v\,\,=\,\,\sqrt{{2gh}}
(b) In case of rough plane the sphere rolls down hence applying conservation of energy we get
\displaystyle mgh\,\,=\,\,\frac{1}{2}\,\,m{{v}^{2}}\,\,\,+\,\,\frac{1}{2}\,\,I{{\omega }^{2}}\,\,\,\,\,\,\,\,\,\,[Where\,\,I\,\,=\,\,\frac{2}{5}\,\,m{{r}^{2}}]
\displaystyle \Rightarrow \,\,\,\,\,mgh\,\,=\,\frac{1}{2}\,\,m{{v}^{2}}\,\,+\,\,\frac{1}{2}\,\,\,\,\left[ {\frac{2}{5}\,\,m{{r}^{2}}} \right]\,\,\,\,{{\left[ {\frac{v}{r}} \right]}^{2}}
\displaystyle \Rightarrow \,\,\,\,\,mgh\,\,=\,\frac{1}{2}\,\,m{{v}^{2}}\,\,+\,\,\frac{1}{5}\,\,m{{v}^{2}}
Hence \displaystyle v\,\,=\,\,\sqrt{{\frac{{10}}{7}\,\,gh}}
Illustration
A spherical ball is given a translation velocity equal to v0 and pushed along a horizontal surface where the coefficient of friction is μ. Calculate when it begins to roll without slipping.
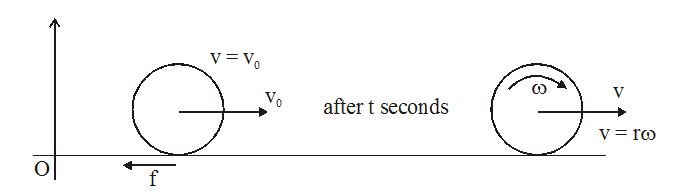
(i) Velocity of centre of mass
(ii) The time taken.
Solution
The point of contact has a forward velocity when the ball starts moving. This causes slipping and hence a kinetic friction equal to µmg acts in backward direction. This frictional force provides a clock-wise torque and hence the angular velocity increases from zero to ω in time t. The same frictional force reduces the linear velocity of centre of mass from v0 to v in time t.
If the ball begins to roll without slipping after time t,
v = rω
Using v = u + at for linear motion of centre of mass,
v = v0 – \displaystyle \left( {\frac{{\mu mg}}{m}} \right)\ t
v = v0 – μ gt … (i)
Using ωf = ωi + at andt = Ia for rotation:
w = 0 + \displaystyle \left( {\frac{{\mu mgr}}{I}} \right)\ t … (ii)
We also have v = rω for pure rolling (iii)
t = \displaystyle \left( {\frac{{{{v}_{0}}{{k}^{2}}}}{{{{k}^{2}}+{{r}^{2}}}}} \right)\ \frac{1}{{\mu g}} (where I = mk2)
and v = \displaystyle \frac{{{{v}_{0}}{{r}^{2}}}}{{{{k}^{2}}+{{r}^{2}}}}
For a solid sphere k2 = 2/5 r2
time (t) = \displaystyle \frac{{2{{v}_{0}}}}{{7\mu g}} and v = 5/7 v0
Hence after \displaystyle \frac{{2{{v}_{0}}}}{{7\mu g}} seconds, the translational speed of ball reduces to 5/7 v0 and it begins to roll without slipping.
Illustration
A solid cylinder of mass M and radius R rolls down an inclined plane with height h without slipping. Find the speed of its centre of mass when it reaches its bottom.
Solution
From COE, mgh = \displaystyle \frac{1}{2}mv2 + \displaystyle \frac{1}{2}Iω2
mgh = \displaystyle \frac{1}{2}mv2 + \displaystyle \frac{1}{2}. ( \displaystyle \frac{1}{2}mR2) ´ \displaystyle \frac{{{{v}^{2}}}}{{{{R}^{2}}}} = \displaystyle \frac{3}{4}mv2
v = \displaystyle \sqrt{{\frac{{4gh}}{3}}}
Illustration
A solid cylinder of radius 4 cm and mass 250 g rolls down an inclined plane (1 in 10). Find the acceleration and the total energy of the cylinder after 5 sec.
Solution: Given that:R=4cm= 0.04m, M=250g = 0.25kg
\sin \alpha =\frac{1}{{10}},
The acceleration of a body rolling down an inclined plane is given by a=\frac{{g\sin \alpha }}{{1+\frac{{{{K}^{2}}}}{{{{r}^{2}}}}}}.
But the M.I. of the solid cylinder about its own axis =I=\frac{1}{2}M{{R}^{2}}=M{{K}^{2}}
Where K = radius of gyration
K=\frac{{{{K}^{2}}}}{{{{R}^{2}}}}=\frac{1}{2}
a=\frac{{g\sin \alpha }}{{1+\frac{1}{2}}} =\frac{2}{3}g\sin \alpha =\frac{2}{3}\times 9.8\times \frac{1}{{10}}\text{m/}{{\text{s}}^{2}}=0.653\ \text{m/}{{\text{s}}^{2}}
Now by 1st equation of motion
v=u+at=0+0.653\times 5\ \text{m/s}=\text{3}\text{.26}\,\text{m/s}
As the cylinder is rolling, the total K.E. of the cylinder is the sum of both K.E. of translation and rotation.
Total K.E. =\frac{1}{2}M{{v}^{2}}+\frac{1}{2}I{{\omega }^{2}} =\frac{1}{2}M{{v}^{2}}+\frac{1}{2}\frac{1}{2}M{{R}^{2}}.\frac{{{{v}^{2}}}}{{{{R}^{2}}}} \left( {\because \ \ \ \ \omega =\frac{v}{R}} \right)
=\frac{3}{4}M{{v}^{2}}=\frac{3}{4}\times 0.25\times {{(3.26)}^{2}}\text{J}=\text{2}\text{.0J}
Illustration
A ring, a disc and a sphere all of the same radius and mass roll down an inclined plane the same height h. Which of the three reaches the bottom (i) earliest, (ii) lastest?
Solution: The acceleration of a body rolling down an inclined plane is given by,
a=g\sin \alpha \left( {\frac{{M{{R}^{2}}}}{{I+M{{R}^{2}}}}} \right)
For a ring, I=M{{R}^{2}}
a=g\sin \alpha \left( {\frac{{M{{R}^{2}}}}{{M{{R}^{2}}+M{{R}^{2}}}}} \right)=\frac{1}{2}g\sin \alpha =0.5g\sin \alpha
For a disc, I=\frac{1}{2}M{{R}^{2}}
a=g\sin \alpha \left( {\frac{{M{{R}^{2}}}}{{\frac{1}{2}M{{R}^{2}}+M{{R}^{2}}}}} \right)=\frac{2}{3}g\sin \alpha =0.67g\sin \alpha
For a sphere, I=\frac{2}{5}M{{R}^{2}}
a=g\sin \alpha \left( {\frac{{M{{R}^{2}}}}{{\frac{2}{5}M{{R}^{2}}+M{{R}^{2}}}}} \right)=\frac{5}{7}g\sin \alpha =0.71\ g\sin \alpha .
Practice Questions (Level-1)
1.
A wheel is in pure rolling condition on a level road. If velocity of centre of mass is then velocity of topmost point is
(a) \overrightarrow{{v\,}}
(b) 2\overrightarrow{{v\,}}
(c) zero
(d) \sqrt{{2\overrightarrow{v}}}
Ans (b)
2.
A sphere rolls down an inclined plane. What fraction of its energy is rotational?
(a) \frac{2}{7}
(b) \frac{3}{7}
(c) \frac{4}{7}
(d) \frac{5}{7}
Ans (a)
3.
A circular disc is rolling down on inclined plane without slipping. If the angle of inclination is 30°, the acceleration of the disc down the inclined plane is
(a) g
(b) \frac{g}{2}
(c) \frac{g}{3}
(d) \frac{{\sqrt{2}}}{3}g
Ans (c)
4.
A body is in pure rolling on horizontal ground and its goes from rough region AB to perfectly smooth region BC. Then in region BC
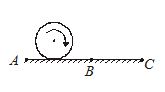
(a) body will stop rolling after some time
(b) body will stop rotating after some time
(c) body will continue rolling
(d) body will start rolling with forward slipping
Ans (c)
5.
The speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height h, from rest without sliding is:
(a) \sqrt{{gh}}
(b) \sqrt{{\left( {\frac{1}{5}} \right)}}gh
(c) \sqrt{{\left( {\frac{4}{3}} \right)}}gh
(d) \sqrt{{\left( {\frac{{10}}{7}} \right)}}gh
Ans (d)
6.
Work done by friction in case of pure rolling:
(a) is always zero
(b) is always positive
(c) is always negative
(d) may be positive and negative
Ans (b)
7.
A Sphere is rolling down a plane of inclination q to the horizontal. The acceleration of its centre, down the plane is:
(a) g sin q
(b) less than g sin q
(c) greater than g sin q
(d) greater than \frac{{g\,\sin \,\theta }}{2}
Ans (b)
8.
A sphere of mass M rolls without slipping on an inclined plane of inclination q. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping?
(a) \frac{2}{5}\tan \theta
(b) \frac{2}{7}\tan \theta
(c) \frac{5}{7}\tan \theta
(d) \tan \theta
Ans (b)
9.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30o. The coefficient of static friction is µs = 0.25.
(a)
How much is the force of friction acting on the cylinder?
(a)12.4 N
(b) 15.3 N
(c)16.4 N
(d) 16.0 N
Ans(c)
(b)
What is the work done against friction during rolling?
(a)0
(b)1
(c)5
(d)9
Ans(a)
(c)
Used, at what value of q does the cylinder begin to skid and not roll perfectly?
(a)40o
(b)30o
(c)25o
(d)37o
Ans(d)
Comprehension Based Question (10 to 12)
Consider a uniform disc of mass m, radius r, rolling without slipping on a rough surface with linear acceleration a and angular acceleration due to an external force F as shown in the figure. Coefficient of friction is µ.
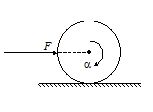
10.
The work done by the frictional force at the instant of pure rolling is
(a) \frac{{\mu mga{{t}^{2}}}}{2}
(b) \mu mga{{t}^{2}}
(c) \mu mg\frac{{a{{t}^{2}}}}{\alpha }
(d) zero
Ans (d)
11.
The magnitude of frictional force acting on the disc is
(a) ma
(b) mmg
(c) \frac{{ma}}{2}
(d) zero
Ans (c)
12.
Angular momentum of the disc will conserved about
(a) center of mass
(b) point of contact
(c) at point at a distance 3R/2 vertical above the point of contact
(d) about a point at a distance 4R/3 vertically above the point of contact
Ans (c)
13.
A disc of mass M and radius R is rolling with angular speed w on a horizontal plane as shown in figure. The magnitude of angular momentum of the disc about O is
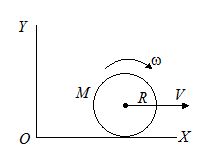
(a) \displaystyle \frac{{M{{R}^{2}}}}{2}\omega
(b) \displaystyle M{{R}^{2}}\omega
(c) \displaystyle \frac{3}{2}M{{R}^{2}}\omega
(d) \displaystyle 2M{{R}^{2}}\omega
Ans (c)
Practice Questions (Level-2)
1.
Find the least coefficient of friction between surfaces of inclined plane (inclination angle = a) and solid cylinder such that cylinder will roll down without slipping
(a) \frac{2}{3}\tan \alpha
(b) \frac{2}{7}\tan \alpha
(c) \frac{1}{3}\tan \alpha
(d) \frac{5}{7}\tan \alpha
Ans (c)
2.
A constant horizontal force F is applied on the top of a solid sphere and a hollow sphere of same mass and radius both kept on a sufficiently rough surface. Let a1 and a2 be their liner accelerations then:
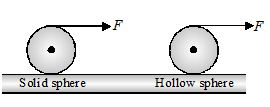
(a) a1 = a2
(b) a1>a2
(c) a1<a2
(d) data insufficient
Ans (b)
3.
A force F acts tangentially at the highest point of the sphere of mass M kept on a rough horizontal plane. If the sphere rolls without slipping, the acceleration of the centre of sphere is:
(a) \frac{{10F}}{{7M}}
(b) \frac{{10F}}{{7M}}
(c) \frac{{10M}}{{7F}}
(d) \frac{{10}}{7}MF
Ans (a)
4.
A ring is kept on a rough surface. But the coefficient of friction is less than the minimum value required for pure rolling. At any instant of time let KT and KR be the translational and rotational kinetic energies of the ring, then
(a) KR = KT
(b) KR> KT
(c) KT> KR
(d) KR = 0
Ans (c)
Comprehension Based Question (5 to 7)
A solid sphere is projected on a rough horizontal ground with initial velocity v and angular velocity w as shown in figure. It is seen that the angular velocity and velocity of center of mass become zero simultaneously after the sphere move a distance d.
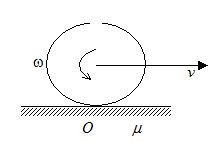
5.
What is the angular momentum of sphere about O?
(a) -\frac{3}{5}m{{r}^{2}}\omega
(b) \frac{3}{5}m{{r}^{2}}\omega
(c) \frac{8}{5}m{{r}^{2}}\omega
(d) zero
Ans (d)
6.
What is relation between v and w?
(a) v=\frac{2}{5}r\omega
(b) v=\frac{{r\omega }}{5}
(c) v=\frac{3}{5}\omega r
(d) v=\frac{{r\omega }}{2}
Ans (a)
7.
What is the work done by friction during motion.
(a) µmgd
(b) \frac{2}{5}\mu mgd
(c) \frac{8}{5}\mu mgd
(d) \frac{7}{2}\mu mgd
Ans (d)
8.
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration a as shown in figure. The magnitude of acceleration of point P at an instant, when its linear velocity is V and angular velocity is w, will be
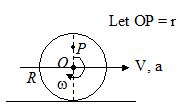
(a) \displaystyle \sqrt{{{{{(a+ra)}}^{2}}+{{{(r{{w}^{2}})}}^{2}}}}
(b) \displaystyle \frac{{ar}}{R}
(c) \displaystyle \sqrt{{{{r}^{2}}{{a}^{2}}+{{r}^{2}}{{w}^{4}}}}
(d) \displaystyle ra
Ans (a)
9.
A solid sphere and a disc of the same mass and radius roll up an incline. Find the ratio of the heights, hs/hd, (Where hsandhd are heights attained by the sphere and the disc respectively) to which they rise if, at the bottom, they have the same
(a)
kinetic energy
(a) 0
(b) 1
(c)3
(d) 5
Ans (b)
(b)
speed
(a)12/17
(b)12/11
(c)14/15
(d)20/7
Ans (c)
10.
The free end of the string wound on the surface of a solid cylinder of mass M and radius R is pulled by a force F applied vertically as shown. If the cylinder rolls on the horizontal surface without slipping, find the maximum angular acceleration that the cylinder can have without losing contact with the surface.
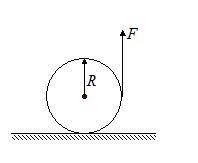
(a) \frac{{2g}}{{5R}}
(b) \frac{{2g}}{{3R}}
(c) \frac{{3g}}{{2R}}
(d) \frac{{5g}}{{3R}}
Ans (b)
11.
A solid sphere of radius R is given a linear velocity voand an angular velocity \frac{{4{{v}_{o}}}}{R} as shown and released on a horizontal rough surface where coefficient of friction is m.
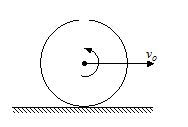
(a)
Find time after which pure rolling starts.
(a) \frac{{5{{v}_{o}}}}{{3\mu g}}
(b) \frac{{10{{v}_{o}}}}{{3\mu g}}
(c) \frac{{3{{v}_{o}}}}{{7\mu g}}
(d) \frac{{10{{v}_{o}}}}{{7\mu g}}
Ans (d)
(b)
How much distance the sphere travels before the start of pure rolling?
(a) \frac{{38v_{o}^{2}}}{{28\mu g}}
(b) \frac{{22v_{o}^{2}}}{{30\mu g}}
(c) \frac{{58v_{o}^{2}}}{{98\mu g}}
(d) \frac{{v_{o}^{2}}}{{\mu g}}
Ans (c)
(c)
What is the position of the sphere from the initial position at which pure rolling starts?
(a) \frac{{40v_{o}^{2}}}{{98\mu g}} [towards right]
(b) \frac{{22v_{o}^{3}}}{{98\mu g}} [towards right]
(c) \frac{{3v_{o}^{-2}}}{{23\mu g}} [towards right]
(d) \frac{{v_{o}^{2}}}{{\mu g}} [towards right]
Ans (a)
(d)
What is the linear velocity of the body at the time of pure rolling?
(a) \frac{2}{5}{{v}_{o}}
(b) \frac{-7}{3}{{v}_{o}}
(c) \frac{-3}{7}{{v}_{o}}
(d) \frac{3}{7}{{v}_{o}}
Ans (d)
(e)
Whether the sphere comes back to its initial position? And if so, after how much time?
(a) yes, after \frac{{30{{v}_{o}}}}{{2\mu g}}
(b) yes, after \frac{{50{{v}_{o}}}}{{21\mu g}}
(c) yes, after \frac{{60{{v}_{o}}}}{{37\mu g}}
(d) yes, after \frac{{48{{v}_{o}}}}{{30\mu g}}
Ans (b)
