Video Lecture
Theory For Making Notes
Relative Velocity In One Dimension
Every motion is relative as it has to be observed with respect to an observer. Relative velocity is a measurement of velocity of an object with respect to other observer. It is defined as the rate of change of relative position of one object w.r.t. to another with time
If an object A is moving with velocity vector \displaystyle \overrightarrow{{{{v}_{{A,G}}}}} ( velocity Of A with respect to ground ) and an object B with velocity \displaystyle \overrightarrow{{{{v}_{{B,G}}}}} ( velocity Of B with respect to ground ), then the velocity of object A relative to object B is given as
\displaystyle \overrightarrow{{{{v}_{{BA}}}}}\,=\,\overrightarrow{{{{v}_{{BG}}}}}\,-\,\overrightarrow{{{{v}_{{AG}}}}}
This can also be written simply as \displaystyle \overrightarrow{{{{v}_{{AB}}}}}\,=\,\overrightarrow{{{{v}_{A}}}}\,-\,\overrightarrow{{{{v}_{B}}}}
The relative velocity of object B relative to object A is
\displaystyle \overrightarrow{{{{v}_{{BA}}}}}\,=\,\overrightarrow{{{{v}_{{BG}}}}}\,-\,\overrightarrow{{{{v}_{{AG}}}}}
Where,
\displaystyle {{v}_{{Ag}}}\,=relative velocity of A with respect to ground.
\displaystyle {{v}_{{Bg}}}\,=relative velocity of B with respect to ground.
\displaystyle {{v}_{{Ag}}}\, and \displaystyle {{v}_{{Bg}}}\, could be written as \displaystyle {{v}_{A}}\, and \displaystyle {{v}_{B}}\, respectively.
Now, we will discuss different cases of relative velocity.
Case I :
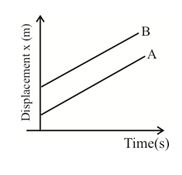
If \displaystyle {{v}_{B}}={{v}_{A}},\,\,{{v}_{B}}-{{v}_{A}}=0, then the two objects A and B stay at a constant distance and their position-time graphs are parallel to each other. Thus, the relative velocity \displaystyle {{v}_{{AB}}} or \displaystyle {{v}_{{BA}}} is zero.
Case –II :
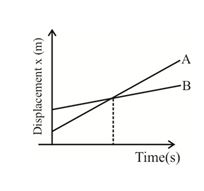
If \displaystyle {{v}_{A}}>{{v}_{B}},\,\,{{v}_{B}}-{{v}_{A}} is negative, then one graph is steeper than the other and they meet at a common point.
Case-III :
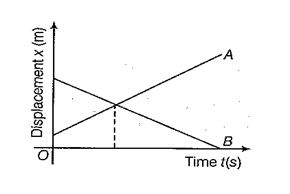
If \displaystyle {{v}_{A}} and \displaystyle {{v}_{B}} are of opposite signs, then the two objects meet at point. e.g., If the objects under consideration are two trains, then for a person sitting on either side, the other trans seem to go very fast.
Case IV :
If both objects A and B move along parallel straight lines in the opposite direction, then relative velocity of B w.r.t. A is given as
\displaystyle {{v}_{{BA}}}={{v}_{B}}-\left( {-{{v}_{A}}} \right)
\displaystyle ={{v}_{B}}+{{v}_{A}}
and the relative velocity of A w.r.t. B is given by
\displaystyle {{v}_{{AB}}}\,=\,\left( {-{{v}_{B}}-{{v}_{A}}} \right)
Illustration
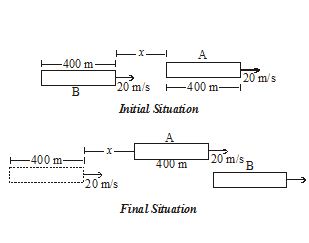
Two trains A and B of length 400m each are moving on two parallel tracks with a uniform speed of 72 \displaystyle km\,{{h}^{{-1}}} in the same direction with A ahead of B. The driver of B decides to overtake A and accelerates by 1 \displaystyle m{{s}^{{-2}}}. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them ?
Solution
Let x = initial distance b/w A & B
w.r.t. A, B travels a distance = \displaystyle x+800\,
\displaystyle \therefore \,\,\,\,\,{{S}_{{B,A}}}\,\,=\,\,x+800
\displaystyle {{u}_{{B,\,A}}}\,\,=\,0
\displaystyle {{a}_{{B,A}}}\,\,=\,\,1\,\,m/{{s}^{2}}
\displaystyle t\,=\,50\,\,\sec
Hence applying \displaystyle {{S}_{{B,\,\,A}}}\,=\,{{u}_{{BA}}}t\,+\,\frac{1}{2}{{a}_{{B,A}}}{{t}^{2}}
\displaystyle x\,+\,800\,=\,0+\frac{1}{2}\times \,1\,\,\times \,\,{{50}^{2}}
\displaystyle \therefore \,\,\,x\,=\,450\,\,m
Illustration
Two towns A and B are connected by a regular bus service with a bus leaving in either direction energy t min. A man cycling with a speed of 20 km/h in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the busses ply on the road l?
Solution
Let v km/h be the constant speed with which the busses plying between the towns A and B. The relative velocity of the bus (for the motion A to B) with respect to the cyclist (i.e., in the direction in which the cyclist is going = ( \displaystyle v-20) \displaystyle km{{h}^{{-1}}}. The relative velocity of the bus from B to A with respect to the cyclist ( \displaystyle v+20) km/h.
The distance travelled by the bus in time T (minutes) = vT
As per question,
\displaystyle \frac{{vT}}{{v-20}}\,=\,18\,\,or\,\,vT\,\,=\,\,18v\,\,-\,18\,\times \,20 …(i)
and \displaystyle \frac{{vT}}{{v-20}}\,=\,6\,\,or\,\,vT\,\,=\,\,6v\,\,+\,20\,\times \,6 ….(ii)
By Eqs. (i) and (ii), we get
\displaystyle 18v\,-\,18\,\times \,20\,\,=\,6v\,\,+\,20\,\,\times \,\,6
Or \displaystyle 12v\,=20\,\times \,6\,\,+\,18\,\,\times \,\,20\,=\,480
Or \displaystyle v\,=\,40\,\,km/h
Putting this value of v in Eq. (i), we get
\displaystyle 40T\,\,=\,\,18\,\,\times \,\,40-18\times \,\,20
= \displaystyle 18\,\,\times \,\,20
Or \displaystyle T\,=\,18\,\times \,\,20/40\,\,=\,9\,\,\min
Illustration
From a lift moving upward with a uniform acceleration ‘a’, a man throws a ball vertically upwards with a velocity v relative to the lift. The ball comes back to the man after a time t. Show that a + g = 2 v/t.
Solution:
Let us consider all the motion from lift frame. Then, the acceleration, displacement and velocity everything will be considered from the lift frame itself.
As the ball comes again to the man, therefore displacement from the lift frame is zero.
Again, the velocity with respect to the lift frame is v.
Similarly, the acceleration with respect the lift frame is
g – (–a) = a + g (downwards)
Now, s = ut + \displaystyle \frac{1}{2}at2
0 = vt – \displaystyle \frac{1}{2} (a+g)t2
or a + g = 2 \displaystyle \frac{v}{t}.
RELATIVE VELOCITY IN TWO DIMENSIONAL MOTION
All the motion study till now is defined with respect to a reference point of a coordinate system i.e. origin O, which is assumed to be at rest. The motion of any object, say A, w.r.t. any other moving object, say B, is termed as relative motion of object A with respect to object B.
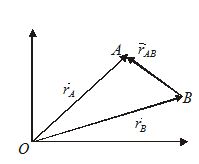
In figure the position vector of A with respect to B can be given as {{\vec{r}}_{{AB}}}={{\vec{r}}_{A}}-{{\vec{r}}_{B}}
Differentiating this equation, we get
\frac{{d{{{\vec{r}}}_{{AB}}}}}{{dt}}=\frac{{d{{{\vec{r}}}_{A}}}}{{dt}}-\frac{{d{{{\vec{r}}}_{B}}}}{{dt}}
or {{\vec{v}}_{{AB}}}={{\vec{v}}_{A}}-{{\vec{v}}_{B}}
Here {{\vec{v}}_{A}} and {{\vec{v}}_{B}} are the velocities of A and B, respectively, with respect to O and {{\vec{v}}_{{AB}}} is the velocity of A w.r.t. B
Differentiating again, we get
\frac{{d{{{\vec{v}}}_{{AB}}}}}{{dt}}=\frac{{d{{{\vec{v}}}_{A}}}}{{dt}}-\frac{{{{{\vec{v}}}_{B}}}}{{dt}}
or \displaystyle \overset{\to }{\mathop{{{{a}_{{AB}}}}}}\,=\overset{\to }{\mathop{{{{a}_{A}}}}}\,-\overset{\to }{\mathop{{{{a}_{B}}}}}\,
(i)
If an object move with uniform relative acceleration, then equations of motions are modified as
\overset{\to }{\mathop{{{{v}_{{rel}}}}}}\,=\overset{\to }{\mathop{{{{u}_{{rel}}}}}}\,+\overset{\to }{\mathop{{{{a}_{{rel}}}}}}\,t
\overset{\to }{\mathop{{{{s}_{{rel}}}}}}\,=\overset{\to }{\mathop{{{{u}_{{rel}}}}}}\,+\frac{1}{2}\overset{\to }{\mathop{{{{a}_{{rel}}}}}}\,{{t}^{2}}
{{v}_{{rel}}}^{2}-{{u}_{{rel}}}^{2}=2\overset{\to }{\mathop{{{{a}_{{rel}}}}}}\,.\overset{\to }{\mathop{{{{s}_{{rel}}}}}}\,
Rain–Man problem
If the rain is falling down with a velocity {{\vec{v}}_{{rain}}} and the man is moving on ground with velocity {{\vec{v}}_{{man}}}, the relative velocity of rain w.r.t. man {{\vec{v}}_{{rel}}} appear different than that it appears to a stationary observer.
Case-I: When rain is falling vertically down
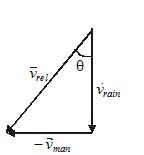
As explain above, the relative velocity of rain with respect to man is given as
{{\vec{v}}_{{rel}}}={{\vec{v}}_{{rain}}}-{{\vec{v}}_{{man}}} ={{\vec{v}}_{{rain}}}+(-{{\vec{v}}_{{man}}})
This equation is represented in figure and it suggest that
{{\vec{v}}_{{rel}}}=\sqrt{{{{v}_{{rain}}}^{2}+{{v}_{{man}}}^{2}}}
The rain appear to man falling down from the front making an angle with vertical given as
\theta ={{\tan }^{{-1}}}\left( {\frac{{{{v}_{{man}}}}}{{{{v}_{{rain}}}}}} \right)
Illustration
During a rainstorm the raindrops are observed to striking ground at an angle of 37° with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed?
Let v= velocity of raindrops relative to earth and {{v}_{w}} wind velocity.
Then {{v}_{x}}={{v}_{w}}. = 4.5 m/s
From figure
{{v}_{y}}=\frac{{{{v}_{w}}}}{{\tan 37{}^\circ }}=6.0\,\,\mathbf{m/s} and v=\sqrt{{{{v}_{x}}^{2}+{{v}_{y}}^{2}}}=7.5\,\,\mathbf{m/s}
Illustration
A man standing on a road has to hold his umbrella at 30° with the vertical to keep the rain away. He throws the umbrella and starts running at 10 km/h. He finds that raindrops are hitting his head vertically. Find the speed of raindrops with respect to (a) the road, (b) the moving man runs is shown in the figure (b)
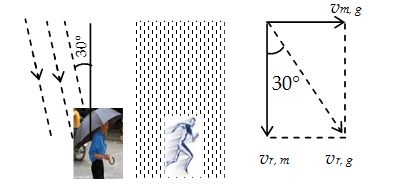
Here \displaystyle {{\overrightarrow{{v\,}}}_{{r,g}}}=velocity of the rain with respect to the ground
\displaystyle {{\overrightarrow{{v\,}}}_{{m,g}}}=velocity of the man with respect to the ground and
\displaystyle {{\overrightarrow{{v\,}}}_{{r,m}}}= velocity of the rain with respect to the man.
We have, \displaystyle {{\overrightarrow{{v\,}}}_{{r,g}}}={{\overrightarrow{{v\,}}}_{{r,m}}}+{{\overrightarrow{{v\,}}}_{{m,g}}} … (1)
Taking horizontal components, equation (1) gives
\displaystyle {{v}_{{r,g}}}\sin 30{}^\circ ={{v}_{{m,g}}}=10km/h
or \displaystyle {{v}_{{r,g}}}=\frac{{10\,\text{km/h}}}{{\sin 30{}^\circ }}=20\text{km/h}
Taking vertical components, equation (1) gives
\displaystyle {{v}_{{r,g}}}\cos 30{}^\circ ={{v}_{{r,\,\,m}}}
or \displaystyle {{v}_{{r,m}}}=(20\text{km/h})\frac{{\sqrt{3}}}{2}
= \displaystyle 10\sqrt{3} km/h
RIVER- BOAT PROBLEM
In a river of width d and flowing with stream of velocity {{\vec{v}}_{{stream}}}, a boat that can move in still water with speed {{\vec{u}}_{{boat}}} is flowing. if its relative speed w.r.t. stream is {{\vec{u}}_{{boat}}} and w.r.t. ground is , then
{{\vec{v}}_{{boat}}}={{\vec{v}}_{{stream}}}+{{\vec{u}}_{{boat}}}
Case-I: Motion up stream
When boat move against stream, its speed w.r.t. ground decreases i.e., {{v}_{{boat}}}={{u}_{{boat}}}-{{v}_{{stream}}}
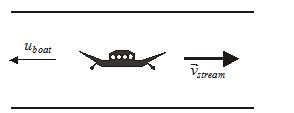
Thus boat will reach its destination if {{u}_{{boat}}}>{{v}_{{stream}}} and it will take time more than required in still water.
Case-II: Motion down stream
In this case, stream add its velocity to the boat and hence w.r.t. ground, the speed of boat increases.
{{v}_{{boat}}}={{u}_{{boat}}}+{{v}_{{stream}}}
Thus, boat reaches its destination point in lesser time.
Case-III: Motion perpendicular to stream
When boat move perpendicular to stream, then its actual direction of motion make some angle with stream and it never reaches a point vertically opposite on other bank of river as shown in figure
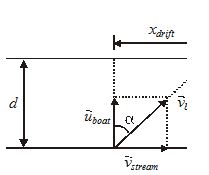
The speed of boat w.r.t. ground is {{v}_{{boat}}}=\sqrt{{{{v}_{{stream}}}^{2}+{{u}_{{boat}}}^{2}}}
and it move in a direction making an angle with stream
\varphi =\frac{\pi }{2}-\alpha =\frac{\pi }{2}-{{\tan }^{{-1}}}\left( {\frac{{{{v}_{{stream}}}}}{{{{u}_{{boat}}}}}} \right)
Time required for crossing the river t=\frac{d}{{{{u}_{{boat}}}}} and drift along the stream {{x}_{{drift}}}={{v}_{{stream}}}t=\frac{{{{v}_{{stream}}}}}{{{{u}_{{boat}}}}}d
Note that this is the minimum time taken by boat to cross-river
Case-IV For minimum drift, i.e. to reach vertically opposite point on the other bank the boat has to move at angle \frac{\pi }{2}+\theta with stream shown in figure
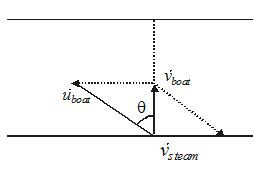
The speed of boat w.r.t. ground is {{v}_{{boat}}}=\sqrt{{{{u}_{{boat}}}^{2}-{{v}_{{stream}}}^{2}}}and it move in a direction making an angle with stream given as \varphi =\frac{\pi }{2}+{{\sin }^{{-1}}}\left( {\frac{{{{v}_{{stream}}}}}{{{{u}_{{boat}}}}}} \right)
Time required for crossing river t=\frac{d}{{{{v}_{{boat}}}}}=\frac{d}{{\sqrt{{{{u}_{{boat}}}^{2}-{{v}_{{stream}}}^{2}}}}}\,\,\,=\,\frac{d}{{u\cos \theta }}
Note that the time required for crossing river is minimum, when, \theta =0{}^\circ i.e. the boat moves perpendicular to stream
Practice Questions (Level-1)
1.
Two cars get closer by 8 m every second while traveling in the opposite directions. They get closer by 0.8 m while traveling in the same directions. What are the speeds of the two cars?
(a) 4 m/s and 4.4 m/s (b) 4.4 m/s and 3.6 m/s
(c) 4 m/s and 3.6 m/s (d) 4 m/s and 3 m/s
Ans (b)
2.
A river is flowing from east to west at a speed of 5 m/min. A man on south bank of river, capable of swimming 10 m/min in still water, wants to swim across the river in shortest time, then he should swim
(a) due north
(b) due north-east
(c) due north-east with double the speed of river
(d) due north-west
Ans (a)
3.
The speed of a boat is 5 km/h in still water. It crosses is river of width 1.0 km along the shortest path in 15 minutes, the velocity of the river water (in km/h)
(a) 5 (b) 1 (c) 3 (d) 4
Ans(c)
4.
In previous question, the angle by which the boat should be rowed with the stream is
(a) 37° (b) 53° (c) 90° (d) 127°
Ans (d)
Practice Questions (Level-2)
1.
A large number of particles are moving towards each other with velocity of magnitude having directions of motion randomly distributed. What is the magnitude of average relative velocity between any two particles averaged over all the pairs?
(a) \frac{{4v}}{\pi } (b) 4\pi v (c) v (d) \pi v/4
Ans (a)
2.
The velocity of a swimmer with respect to the ground is u. In what direction w.r.t. the stream should the swimmer swim in order to reach a point just in front of the starting point, if is the speed of river flow
(a) \frac{\pi }{2}+{{\sin }^{{-1}}}\left( {\frac{u}{{\sqrt{{{{u}^{2}}+{{v}^{2}}}}}}} \right) (b) \frac{\pi }{2}+{{\sin }^{{-1}}}\left( {\frac{v}{{\sqrt{{{{u}^{2}}+{{v}^{2}}}}}}} \right)
(c) \frac{\pi }{2}+{{\sin }^{{-1}}}\left( {\frac{v}{u}} \right) (d) \frac{\pi }{2}+{{\sin }^{{-1}}}\left( {\frac{u}{v}} \right)
Ans (c)
3.
Two particles A and B connected by a rigid rod AB. The rod slides along two perpendicular rails as shown. The velocity of A to the left is 10 m/s. What is the velocity of B, when angle\alpha =37{}^\circ ?
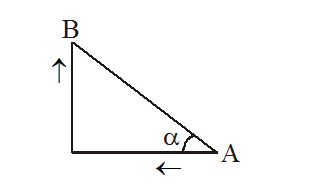
(a) 5.8 m/s (b) 9.8 m/s (c) 11.2 m/s (d) 13.3 m/s
Ans (d)
4.
A monkey is climbing up a tree at a speed of 3 m/s. A dog runs towards the tree with a speed of 4 m/s. What is the relative speed of the dog as seen by the monkey?
(a) >7 m/s (b) between 5 m/s and 7 m/s
(c) 5 m/s (d)< 5 m/s
Ans (c)
5.
An elevator, in which a man is standing, is moving upward with a speed of 10 m/s. If the man drops a coin from a height of 2.45 metre, it reaches the floor of the elevator after a time (g=9.8\,\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}}).
(a) \sqrt{2}\,\mathbf{s} (b) \sqrt{2}\,\mathbf{s} (c) 2 s (d) \frac{1}{2}\,\mathbf{s}
Ans (b)
6.
Four persons K, L, M and N are initially at the four corners of a square of side . Each person now move with a uniform speed in such a way that K always headed toward L, L toward M, M toward N and N always headed toward K. After how much time will the four persons meet?
(a) d/v (b) d/\sqrt{2}v
(c) \sqrt{2}d/v (d)d/2v
Ans (d)
7.
A glass windscreen whose inclination with the vertical can be changed is mounted on a car. The car moves horizontally with a speed of 2 m/s. At what angle with the vertical should the windscreen be placed so that the raindrops, which are falling vertically downwards with speed 6m/s, strike the windscreen perpendicularly?
(a) {{\tan }^{{-1}}}\frac{1}{3} (b) {{\tan }^{{-1}}}(3) (c) {{\cos }^{{-1}}}(3) (d) {{\cos }^{{-1}}}\frac{1}{3}
Ans (b)
8.
A motorboat covers the distance between two stations on the river t1 = 8h and t2 =12h downstream and upstream respectively. What is the time required for the boat to cover this distance in still water ?
(a) 5.0 h
(b) 2.5 h
(c) 9.6 h
(d) 10 h
Ans (C)
9.
A passenger sitting by the window of a train moving with a velocity v1 = 72 km/h observes for 10 s a train moving with a velocity v2 = 32.4 km/h in the opposite direction. Find the length of the second train.
(a) 290 m
(b) 220 m
(c) 200 m
(d) 250 m
Ans (a)
10.
Raindrops fall vertically at a speed of 20 m/s. At what angle do they fall on the windscreen of a bus moving with a velocity of 54 km/h if the windscreen of the bus is vertical ?
(a) 35°
(b) 33°
(c) 37°
(d) 40°
Ans (c)
11.
Two cyclists move towards each other. The first cyclist, whose initial velocity vo1 = 5.4 km/h, descends the hill, gathering speed with an acceleration a1= 0.2 m/s2. The second cyclist, whose initial velocity vo2= 18 km/h. climbs the hill with an acceleration a2= -0.2 m/s2. How long does it take for the cyclist to meet if the distance x0separating them at the initial instant of time is 195 m ?
(a) 15 s
(b) 30 s
(c) 50 s
(d) 55 s
Ans (b)
12.
A motorboat going downstream overcame a raft at point A; to = 60 minutes later it turned back and after sometime passed the raft at a distance l = 6.0 km from the point A. Find the velocity of the river.
(a) 3 km/h
(b) 8 km/h
(c) 16 km/h
(d) 20 km/h
Ans (a)



