Video Lecture
Theory For Making Notes
Reflection and Refraction
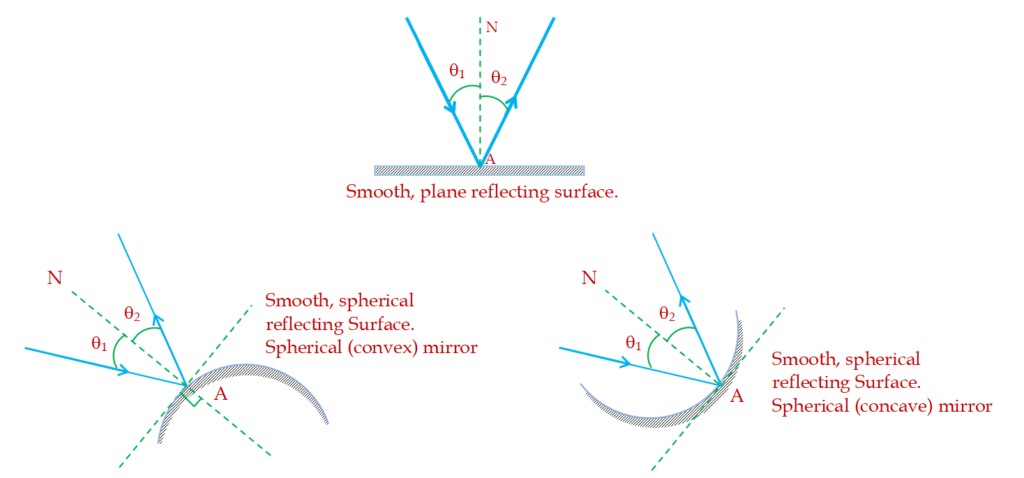
When a light ray traveling in a medium encounters a perfectly reflecting boundary, all the incident ray is reflected back in to the same medium. It is found experimentally that the incident ray, the reflected ray and the normal to the reflecting surface lie in the same plane.
Consider a light ray traveling in air and incident at an angle \displaystyle {{\theta }_{1}} with the normal (AN) and reflected at an angle \displaystyle {{\theta }_{2}} with the normal.
Experiments shows that angle of reflection ( \displaystyle {{\theta }_{2}}) equals the angle of incidence ( \displaystyle {{\theta }_{1}}) irrespective of the type of mirror
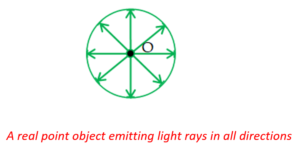
Object and Image
A point source of light is a real object in general. A real object is suppose to emit infinite number of light rays.
A point is called image where the reflected or refracted light rays intersect (real image) or appear to intersect (virtual image).
Note that for image formation at least two rays should be drawn from the real object and are allowed to fall on the reflecting or refracting surface. The rays are traced after reflection or refraction and analyzed. There may be two possibilities
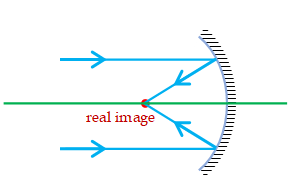
- After reflection or refraction the rays will intersect on their own as shown in the figure, Then the point of their intersection is called a real image
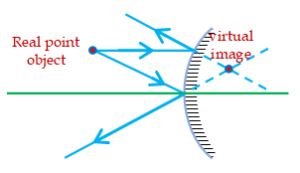
- After reflection or refraction the rays will diverge and will never meet in space as shown in the diagram. In this case the rays are produced back till they intersect at a point. This point of intersection is called a virtual image.
Concept Of Virtual Point Object
In some optical systems which contains two or more mirrors or lenses ( like telescopes , microscopes etc) the intermediate images (other than the first object and the last final image) may be considered as a virtual object.A virtual object is formed when the reflected or refracted rays are intercepted by a lens or mirror and shift the position of the image as shown in the diagram.
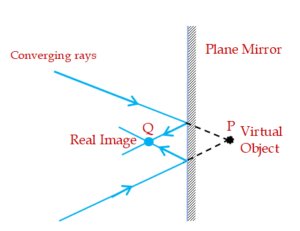
In the diagram the converging rays are coming from a converging lens or mirror that is not shown in the diagram. A plane mirror is intercepting the converging rays and reflect them toward point Q at which a real image is formed. Now for this real image what is the object? So answer is that the object is P where the converging rays would meet without placing plane mirror. But due to plane mirror,since this object is not actually there, therefore it is considered as a virtual object.Take care that we can’t start fresh light rays from a virtual object.
Reflection From A Plane Mirror
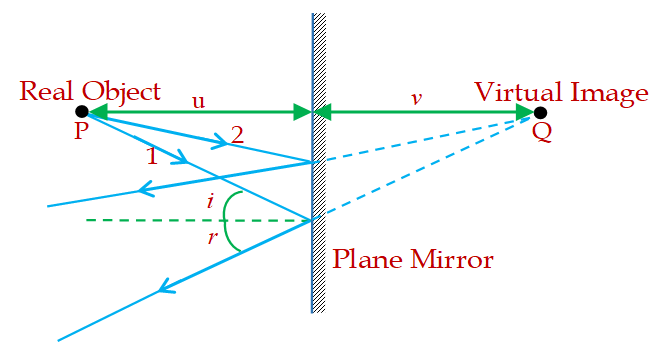
Consider a point object P in front of a plane mirror. As discussed earlier for its image we start two rays 1 and 2 which fall on the mirror and reflected back following the law of reflection i.e. \displaystyle \angle i=\angle r. The reflected rays become diverging after reflection from the mirror, hence they never meet in front of the mirror.
Therefore we produce them backward to meet at Q behind the mirror. So Q is the virtual image of the point object P. Hence we conclude that a plane mirror always form virtual image of a real object.
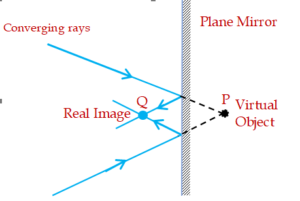
But at the same time it can also produce a real image if the object is virtual as shown in the diagram given below.
Important points for a plane mirror
- Image is as far behind the mirror as the object in front. Hence u = v (From geometry)
Image is un-magnified, virtual for a real object and upright (erect)
Deviation produced by plane mirror
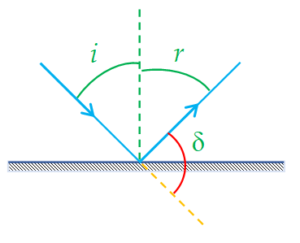
(a) Single reflection: A mirror can produce a change in the path of a light ray. Therefore the ray is said to be deviated from its path. The angle of deviation is defined as the angle between the reflected ray (also called deviated ray) and the extension of the actual ray (shown by dotted line in the diagram.
The deviation suffered by incident ray due to reflection can be found from the diagram as
\displaystyle \delta =\pi -(i+r), since i=r
therefore \displaystyle \delta =\pi -2i
The relation between \displaystyle \delta and i is a linear equation. Hence graph between them is a straight line of negative slop.
The graph shows that as the angle of incidence varies from zero to \displaystyle \pi /2 the deviation angle varies from zero to \displaystyle \pi .
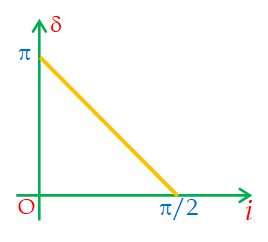
special case I: When i = 0 (normal incidence)
\displaystyle {{\delta }_{{\max }}}=\pi
special case II: When i = \displaystyle \frac{\pi }{2} (Grazing incidence)
\displaystyle {{\delta }_{{\min }}}=0
(b) Multiple reflection: In this case net deviation suffered by incident ray is algebraic sum of deviation due to individual reflection.
\displaystyle {{\delta }_{{net}}}=\Sigma {{\delta }_{i}}
Where \displaystyle {{\delta }_{i}}= Deviation due to single reflection
Note that while summing up, sense of rotation is taken into account.
Rotation of mirror
Let’s consider a case when we rotate a plane mirror without changing the incident ray `I’. Let i be angle of incidence in first position of mirror \displaystyle {{M}_{1}}{{M}_{2}} as shown in the figure.
Further, let mirror is rotated through angle \displaystyle \theta , as shown by red dotted position. As a result the normal will also rotate by same angle in same sense from \displaystyle {{N}_{1}} to \displaystyle {{N}_{2}}. Due to rotation of mirror the reflected light is rotated from position \displaystyle {{R}_{1}} to \displaystyle {{R}_{2}} through an angle \displaystyle \phi .
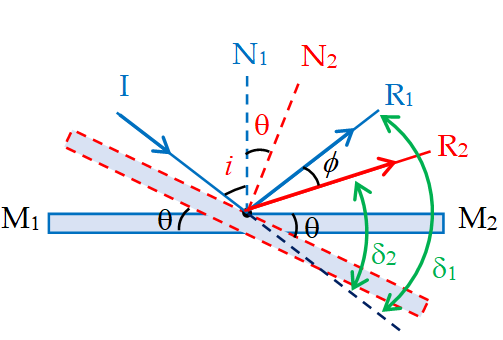
Further, let mirror is rotated through angle \displaystyle \theta , as shown by red dotted position. As a result the normal will also rotate by same angle in same sense from \displaystyle {{N}_{1}} to \displaystyle {{N}_{2}}. Due to rotation of mirror the reflected light is rotated from position \displaystyle {{R}_{1}} to \displaystyle {{R}_{2}} through an angle \displaystyle \phi .
Where \displaystyle \phi ={{\delta}_{1}}-{{\delta }_{2}}
\displaystyle {{\delta}_{1}}= Deviation of light in first position of mirror
\displaystyle {{\delta}_{1}}= \displaystyle \pi -2i
\displaystyle {{\delta }_{2}}= Deviation of light in second position of mirror
\displaystyle {{\delta }_{2}}= \displaystyle \pi -2(\theta +i)
hence
\displaystyle \phi ={{\delta }_{1}}-{{\delta }_{2}}
\displaystyle \phi =\pi -2i-[\pi -2(\theta +i)]
\displaystyle \phi =2\theta .
Thus, the angle turned by the reflected ray is twice the angle turned by the mirror. So, if a mirror turns through a certain angle, keeping incident ray fixed the reflected ray turns through double that angle in same sense i.e., if mirror rotates clockwise then reflected ray will also rotate clockwise.
Note:
(i) The above statement is valid for rotation of mirror about any point.
(ii) If mirror is kept fixed and incident rays are rotated then reflected ray will rotate in opposite sense by same angle.
(iii) If mirror and incident ray both are rotated then net rotation suffered by reflected ray will be algebraic sum of rotation suffered by reflected ray due to mirror rotation and incident ray rotation separately keeping sense of rotation in mind.
Velocity of image
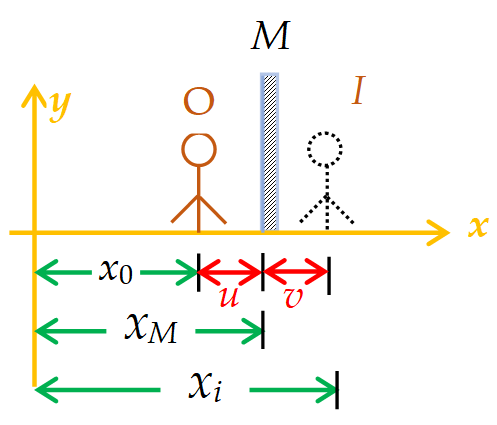
\displaystyle {{x}_{o}} = x co-ordinate of object
\displaystyle {{x}_{M}} = x co-ordinate of mirror
\displaystyle {{x}_{i}} = x co-ordinate of image
Consider an object O standing in front of a plane mirror. Then image is formed behind mirror, such that \displaystyle u={{x}_{M}}-{{x}_{o}} and \displaystyle v={{x}_{i}}-{{x}_{M}} ( from the figure)
but \displaystyle u=v
hence
\displaystyle {{x}_{M}}-{{x}_{o}}={{x}_{i}}-{{x}_{M}}
or
\displaystyle {{x}_{i}}=2{{x}_{M}}-{{x}_{o}}
for velocity of image differentiate the above equation of \displaystyle {{x}_{i}} w.r.t. time `t’. Hence
Velocity of image = \displaystyle {{v}_{i}}=\frac{{d{{x}_{i}}}}{{dt}}
or
\displaystyle {{v}_{i}} = \displaystyle 2\frac{d{{x}_{M}}}{{dt}}-\frac{{d{{x}_{0}}}}{{dt}}
here \displaystyle \frac{d{{x}_{M}}}{{dt}} is the velocity of the mirror i.e. \displaystyle {{v}_{M}} and \displaystyle \frac{d{{x}_{o}}}{{dt}} is the velocity of the object i.e. \displaystyle {{v}_{o}} .
therefore
\displaystyle {{v}_{i}}=2{{v}_{M}}-{{v}_{o}}
So, this is the relation among velocities of image, mirror and object respectively.
All velocities are w.r.t. a fixed point that is origin. But the velocities do not depend on the location of origin.
Note that velocities are vectors hence give a proper sign to the known velocities according to the +ve and –ve x axis that is towards right are taken positive and towards left are taken negative.
If the object starts moving parallel to mirror, then
\displaystyle {{y}_{i}}={{y}_{o}}
or \displaystyle \frac{{d{{y}_{i}}}}{{dt}}=\frac{{d{{y}_{o}}}}{{dt}}
hence \displaystyle {{v}_{i}}={{v}_{o}}
Velocity of image with respect to observer is then calculated using basic equation of relative motion,
\displaystyle \overrightarrow{{{{V}_{{A/B}}}}} = velocity of A w.r.t. B = \displaystyle \overrightarrow{{{{V}_{A}}}}-\overrightarrow{{{{V}_{B}}}}.
Note:
(i) The minimum height of mirror to see full image of a person of height (h) is \displaystyle {{h}_{m}}=\frac{h}{2}.
(ii) When two mirrors are inclined at an angle ‘ \displaystyle \theta ’ the number of images formed is
(1) \displaystyle n=\frac{{360}}{\theta }-1 when \displaystyle \frac{{360}}{\theta } is an even integer
(2) n = \displaystyle \frac{{360}}{\theta } is an odd integer and if \displaystyle \frac{{360}}{\theta } is in fraction then n is equal to integral part of \displaystyle \frac{{360}}{\theta }.
Illustration
Find the velocity of image in the following situation.
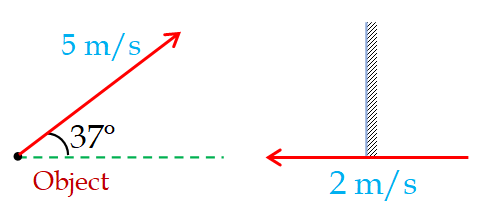
Solution
For velocity of image perpendicular to mirror,
\displaystyle {{({{V}_{I}})}_{x}}=2{{V}_{A}}-{{V}_{0}}
or \displaystyle {{({{V}_{I}})}_{x}} = 2 (– 2) – ( 5 cos \displaystyle {{37}^{o}})
hence \displaystyle {{({{V}_{I}})}_{x}} = – 8 m/s
(–) sign indicates image is moving towards left.
For velocity of image parallel to mirror,
\displaystyle {{({{V}_{I}})}_{y}}= \displaystyle{{({{V}_{0}})}_{y}}
= \displaystyle5\sin 37{}^\circ =+3\text{m/s}
or Velocity of image = \displaystyle \sqrt{{-{{8}^{2}}+{{3}^{2}}}},
hence Velocity of image = \displaystyle \sqrt{{73}}\,\,m/s
and \displaystyle \theta ={{\tan }^{{-1}}}\left( {\frac{3}{8}} \right)
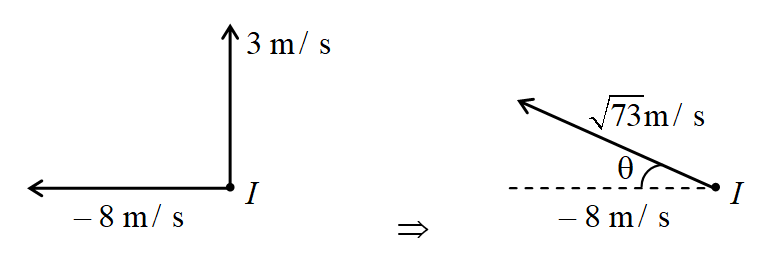
Illustration
Find the smallest size of looking glass, a person with a face 24 cm × 16 cm should purchase, to enable him to see his whole face at a time assuming
(a) man is one eyed
(b) man is two eyed
Given : the separation between his eyes is 8 cm.
Solution
(a) For one eyed man, the required size is 12 cm × 8 cm
(b) For two eyed man : Smallest length of mirror = Half the length of face= ½ × 24 = 12 cm
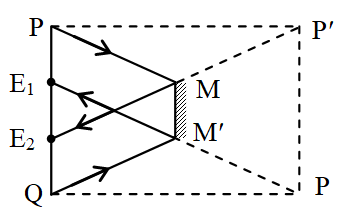
Smallest breadth of the mirror is calculated using the fact the rays from extreme part of face should reach one of the eye after reflection from mirror. The common overlapping portion is required size. The ray diagram is shown in figure.
From figure
MM’ = ½ PQ – ½ E1 E2
= ½ (16 – 8) = 4 cm.
Hence, the shortest size of mirror is 12 cm \displaystyle \times 4 cm.
Illustration
Two plane mirrors are inclined to each other at an angle q. A ray of light is reflected first at one mirror and then at the other. Find the total deviation of the ray.
Solution
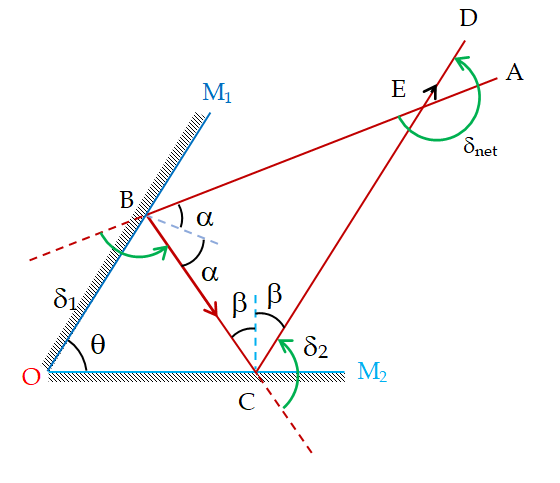
Let
\displaystyle \alpha = Angle of incidence for \displaystyle {{M}_{1}}
\displaystyle \beta = Angle of incidence for \displaystyle {{M}_{2}}
\displaystyle {{\delta }_{1}} = Deviation due to \displaystyle {{M}_{1}}
\displaystyle {{\delta }_{2}} = Deviation due to \displaystyle {{M}_{2}}
From figure ,
\displaystyle {{\delta }_{1}}=\pi -2\alpha ,
\displaystyle {{\delta }_{2}}=\pi -2\beta
Also ray is rotated in same sense i.e., anticlockwise
\displaystyle {{\delta }_{{net}}} = Total deviation = \displaystyle {{\delta }_{1}}+{{\delta }_{2}}
= \displaystyle 2\pi -2(\alpha +\beta )
Now in \displaystyle \Delta OBC, \displaystyle \angle OBC + \displaystyle \angle BCO + \displaystyle \angle COB = \displaystyle {{180}^{o}}
\displaystyle 90{}^\text{o}\,-\,\alpha \,+\,90{}^\text{o}-\beta \,+\,\theta =180{}^\text{o}
\displaystyle \theta =\alpha \,+\,\beta \,\,
\displaystyle \therefore \,\,{{\delta }_{{net}}}\,=\,2\pi -2\theta \,=\,2\left( {\pi -\theta } \right)
Illustration
A ray of light is incident on a plane mirror along a vector \displaystyle \hat{i}+\hat{j}-\hat{k}. The normal on incidence point is along \displaystyle \hat{i}+\hat{j}. Find a unit vector along the reflected ray.
Solution
Reflection of a ray of light is just like an elastic collision of a ball with a horizontal ground component of incident ray along the inside normal gets reversed while the component perpendicular to it remains unchanged. Thus the component of incident ray vector \displaystyle \overrightarrow{A}\,=\hat{i}+\hat{j}-\hat{k} parallel to normal, i.e. \displaystyle \hat{i}+\hat{j} gets reversed while perpendicular to it, i.e., \displaystyle -\hat{k} remains unchanged. Thus, the reflected ray can be written as,
\displaystyle \overrightarrow{R}=-\hat{i}-\hat{j}-\hat{k}
or A unit vector along the reflected ray will be,
\displaystyle \hat{r}=\frac{{\overrightarrow{R}}}{R}=\frac{{-\hat{i}-\hat{j}-\hat{k}}}{{\sqrt{3}}}
or
\displaystyle \hat{r}=-\frac{1}{{\sqrt{3}}}(\hat{i}+\hat{j}+\hat{k})
Q.1
A beam of light starting from point A reflects from a mirror M and forms an image at B as shown in the same horizontal plane as A. For small angle of incidence i, AB is equal to
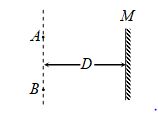
(a) iD (b) 2iD (c) 4iD (d) iD/2
Ans. (b)
Q.2
Two plane mirrors A and B are aligned parallel to each other as shown in figure. A light ray is incident at an angle of 30° at a point just inside one end of A. The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (including the first one) before it emerges out is
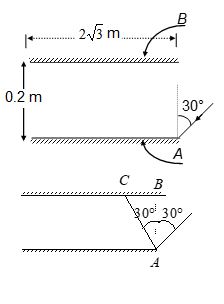
(a) 28 (b) 30 (c) 32 (d) 34
Ans. (b)
Practice Questions (JEE Main Level)
Q.1
Two mirrors labeled L1 for left mirror and L2 for right mirror in the figure are parallel to each other and 3 m apart. A person standing x m from the right mirror L2 looks into this mirror and sees a series of images. The distance between the first and second image is 4 m. Then the value of x is
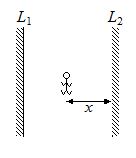
(a) 2 m
(b) 6 m
(c) 1 m
(d) 8 m
Ans (c)
Q.2
A person walks at a velocity v in a straight line forming an angle \displaystyle \theta with the plane of a plane mirror. The velocity \displaystyle {{v}_{{rel}}} with which he approaches his image?
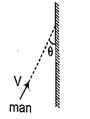
(a) \displaystyle 2v\,\sin \theta
(b) \displaystyle v\,\sin \frac{\theta }{2}
(c) \displaystyle 2v\,\cos \theta
(d) \displaystyle v\,\cos \frac{\theta }{2}
Ans (a)
Q.3
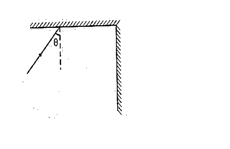
Two plane mirrors are arranged at right angles to each other as shown in figure. A ray of light is incident on the horizontal mirror at an angle \displaystyle \theta . For what value of \displaystyle \theta the ray emerges parallel to the incoming ray after reflection from the vertical mirror?
(a) 60º
(b) 30º
(c) 45º
(d) All of these
Ans (b)
Q.4
Two plane mirrors are inclined at angle as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then \displaystyle \theta is equal to
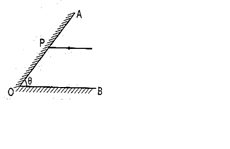
(a) 90º
(b) 60º
(c) 45º
(d) 30º
Ans (b)
Q.5
A man is walking under an inclined mirror at a constant velocity v along the x-axis. If the mirror is inclined at an angle with the horizontal then what is the velocity of the image?
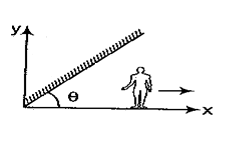
(a) \displaystyle v\,\sin \,\theta \,\hat{i}\,+\,v\,\cos \,\theta \hat{j}
(b) \displaystyle v\,\cos \,\theta \hat{i}\,+\,v\,\sin \,\theta \,\hat{j}
(c) \displaystyle v\,\sin \,2\theta \hat{i}\,+v\,\cos \,2\theta \hat{j}
(d) \displaystyle v\,\cos \,2\theta \hat{i}\,+\,v\,\sin \,2\theta \hat{j}
Ans (d)
Q.6
A person’s eye is at a height of 1.5 m. He stands infront of a 0.3 m long plane mirror whose lower end is 0.8 m above the ground. The length of the image he sees of himself is
(a) 1.5 m (b) 1.0 m (c) 0.8 m (d) 0.6 m
Ans. (d)
Q.7
Two plane mirrors A and B are parallel to each other and spaced 20 cm apart. An object is kept in between them at 15 cm from A. Out of the following, at which point image is not formed in mirror A (distance measured from mirror A)
(a) 15 cm (b) 25 cm (c) 45 cm (d) 55 cm
Ans. (c)
Q.8
A plane mirror is placed at origin parallel to y-axis, facing positive x-axis. An object starts from (2m, 0, 0) with a velocity of ( \displaystyle \left( {2\hat{i}+2\hat{j}} \right)\,m/s. The relative velocity of image with respect to object is along
(a) positive x-axis
(b) negative x-axis
(c) positive y-axis
(d) negative y-axis
Ans. (b)
Q.9
A ray is travelling along x-axis in negative x-direction. A plane mirror is placed at origin facing the ray. What should be the angle of plane mirror with the x-axis so that the ray of light after reflecting from the plane mirror passes through point (1m, \displaystyle \sqrt{3}\,m)?
(a) 30º (b) 60º (c) 45º (d) 90º
Ans. (b)
Q.10
A man is walking under an inclined mirror at a constant velocity v along the x-axis. If the mirror is inclined at an angle with the horizontal then what is the velocity of the image?
(a) \displaystyle v\,\sin \,\theta \,\hat{i}\,+\,v\,\cos \,\theta \hat{j}
(b) \displaystyle v\,\cos \,\theta \hat{i}\,+\,v\,\sin \,\theta \,\hat{j}
(c) \displaystyle v\,\sin \,2\theta \hat{i}\,+v\,\cos \,2\theta \hat{j}
(d) \displaystyle v\,\cos \,2\theta \hat{i}\,+\,v\,\sin \,2\theta \hat{j}
Ans. (d)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
