Video Lecture
Theory For Notes Making
Free and Damped Oscillations
In reality, a spring won’t oscillate forever with constant amplitude. These constant amplitude oscillations (which will really occur in vacuum) are called ‘free oscillations’.
Frictional forces diminish the amplitude of oscillation until eventually the system comes to rest. We will now add frictional forces to the mass and spring. Imagine that the mass was put in a viscous liquid. To incorporate friction, we can just say that there is a frictional force that’s proportional to the velocity of the mass. This is a pretty good approximation for a body moving at a low velocity in air, or in a liquid. So we say the frictional force \displaystyle {{f}_{r}}=-bv. The constant b depends on the kind of liquid and the shape of the mass. The negative sign, just says that the force is in the opposite direction to the body’s motion. Let’s add this frictional force the equation \displaystyle {{f}_{{net}}}=ma.
\displaystyle -kx-bv\,=\,ma
In terms of derivatives
\displaystyle m\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}+b\frac{{dx}}{{dt}}\,+\ kx=0
In the solution of this type of differential equation instead of the amplitude being constant, it’s decaying with time.
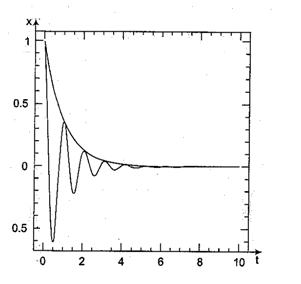
\displaystyle A\left( t \right)\,=\,{{A}_{0}}{{e}^{{-const\,t}}}
So,
\displaystyle x\left( t \right)\,=\,A\left( t \right)\,\cos \,\,\left( {\omega t\,+\,\delta } \right)\,=\,{{A}_{0}}{{e}^{{-\operatorname{co}nst\,\,t}}}\,\cos \,\,\left( {\omega t+\delta } \right)
Here’s a plot of an example of such a function. These types of oscillations which eventually come to end are called ‘damped oscillations’. There are further three types of damped oscillations, namely
(i) Under damped
(ii) Critically damped and
(iii) Over damped oscillations
But their detailed discussion is out of our syllabus at this stage.
Natural frequency (or Characteristic Frequency)
That is the frequency at which a system would oscillate by itself if displaced. The natural frequency of a spring-mass system is \displaystyle {{f}_{0}}=\frac{1}{{2\pi }}\sqrt{{\frac{k}{m}}}, where k is the spring constant and m is the mass of the object attached to the spring.
Forced oscillations
A periodic force at a given frequency (called driving frequency \displaystyle {{f}_{d}}) is applied to an oscillating system of natural frequency \displaystyle {{f}_{0}}. At the beginning (transient stage), there is a mixture of two kinds of oscillations, one has the frequency \displaystyle {{f}_{0}} and the other has \displaystyle {{f}_{d}}. The former will gradually die out because of the damping effect. Eventually (at the steady state) the system settles down with oscillation at the frequency of the driving force ( \displaystyle {{f}_{d}}).
Resonance and its Consequences
When the driving frequency is at the same frequency as the natural frequency of the oscillator, the amplitude of oscillation is at its greatest. When this happens the energy of the oscillator becomes maximum. This is called the condition of resonance.
Physics is full of examples of resonance; building up the oscillations of a child on a swing by pushing with a frequency equal to the swing’s natural frequency is one. Inexpensive loudspeakers often have an unwanted boom or buzz when a musical note happens to coincide with the resonant frequency of the speaker cone. Resonance also occurs in electric circuits; a tuned circuit in a radio or television receiver responds strongly to waves having frequencies near its resonant frequency, and this fact is used to select a particular station and reject the others.
Resonance in mechanical systems can be destructive. A company of soldiers once destroyed a bridge by marching across it in step; the frequency of their steps was close to the natural vibration frequency of the bridge, and the resulting oscillation had large enough amplitude to tear the bridge apart, Ever since, marching soldiers have been ordered to break step before crossing a bridge.
Superposition of two SHM’s
When a particle is subjected to more than one linear SHM then the particle follows a new path which can be linear or non-linear depending upon the direction of displacement given by individual SHMs. Now two cases arise in the superposition.
(i) When two SHM are collinear
(ii) When two SHM are mutually perpendicular.
Superposition of two Collinear SHMs
Let two SHM x1 = a1 sin wt and x2a2 sin (wt + f) are superimposed. The resultant displacement is given by
x = x1 + x2 = a1 sin wt + a2sin (wt + f).
As the amplitudes a1 and a2 are phasors therefore when two SHM are added algebraically their amplitude follow law of vector addition, and hence resultant amplitude is given by \displaystyle R=\sqrt{{a_{1}^{2}+a_{2}^{2}+2{{a}_{1}}{{a}_{2}}\cos \phi }}.
Thus the resultant displacement is given by x = R sin (wt + f) where \displaystyle \phi ={{\tan }^{{-1}}}\left( {\frac{{{{a}_{2}}\sin \phi }}{{{{a}_{1}}+{{a}_{2}}\cos \phi }}} \right).
Superposition of two mutually perpendicular SHM
Consider the SHM x = a sin wt and y = b sin (wt + f) if they are superimposed over a particle then the body starts following a nonlinear path called Lissajous figure and the equation of path can be obtained by eliminating t from the equation of x and y.
y = b sin (wt + f) = b(sin wt cos f + cos wtsin f)
Hence \displaystyle \frac{y}{b}=\sin \omega t\cos \phi +\cos \omega t\sin \phi …(i)
From x = a sin wt we get, \displaystyle \sin \omega t=\frac{x}{a} and \displaystyle \cos \omega t=\sqrt{{1-{{x}^{2}}/{{a}^{2}}}}.
Substituting the values of sin wt and cos wt in equation (i) we get
\displaystyle \frac{y}{b}=\frac{x}{a}\cos \phi +\sqrt{{1-{{x}^{2}}/{{a}^{2}}}}.\sin \phi
Hence \displaystyle \frac{y}{b}-\frac{x}{a}\cos \phi =\sqrt{{1-\frac{{{{x}^{2}}}}{{{{a}^{2}}}}}}\sin \phi
On squaring both sides and solving we get
\displaystyle \frac{{{{y}^{2}}}}{{{{b}^{2}}}}+\frac{{{{x}^{2}}}}{{{{a}^{2}}}}-\frac{{2xy}}{{ab}}\cos \phi -{{\sin }^{2}}\phi =0 …(ii)
which is the equation of an ellipse. Hence we can get the following cases
(a) If \displaystyle \phi =\frac{\pi }{2} the equation (ii) becomes \displaystyle \frac{{{{y}^{2}}}}{{{{b}^{2}}}}+\frac{{{{x}^{2}}}}{{{{a}^{2}}}}=1 which is the equation of a symmetrical ellipse.
(b) If \displaystyle \phi =\frac{\pi }{2} and a = b then equation (ii) becomes x2 + y2 = a2 which is the equation of a circle of radius a.
Illustration
The displacement of a particle executing period motion is given by y=4{{\cos }^{2}}\left( {\frac{1}{2}t} \right)\sin (100\,t).
Find independent constituents of simple harmonic motion.
Solution:
y=4{{\cos }^{2}}\left( {\frac{1}{2}t} \right)\sin (100t),\,\,\,y=2(1+\cos t)\,\sin (1000t) 2{{\cos }^{2}}\theta =1+\cos 2\theta
y=2\sin 1000\,t+2\sin 1000t\times \cos \,t
y=\,\,\,2\sin \,1000t+\sin 1001t+\sin 999\,t [2\sin \,A\cos B=\sin \,(A+B)+\sin (A-B)]
The equations are {{y}_{1}}=2\sin 1000\,t,\,\,\,\,{{y}_{2}}=\sin 1001t,\,\,\,and {{y}_{3}}=\sin 999t.
Objective Assignment
Q.1
A simple harmonic motion is given by the equation x = 3 sin 3 p t + 4 cos 3 p t where x is in metres. The amplitude of the motion is
(a) 3 m (b) 4 m (c) 5 m (d) 7 m
Ans : (c)
Q.2
A particle is subjected to two mutually perpendicular SHM such that x = 2 sin wt and y = 2 sin [wt + (p/4). The path of the particle will be:
(a) An ellipse
(b) A straight line
(c) A parabola
(d) A circle
Ans. (a)
Q.3
Equation of a simple harmonic motion is given as
x = 3 sin 20pt + 4 cos 20 pt
where x is in cms and t in seconds. The amplitude is:
(a) 7 cm (b) 4 cm (c) 5 cm (d) 3 cm
Ans. (C)
Q.4
The composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of p results in the displacement of the particle along
(a) circle (b) figure of eight (c) straight line (d) ellipse
Ans. (c)
Q.5
A particle is subjected to two mutually perpendicular simple harmonic motions such that its x and y coordinates are given by
\displaystyle \frac{{{{d}^{2}}}}{{2D\lambda }} The path of the particle will be
(a) a straight line (b) a circle (c) an ellipse (d) a parabola
Ans. (c)
Q.6
Two simple harmonic motions A and B are given respectively by the following equations
\displaystyle \frac{1}{{2\pi \sqrt{{LC}}}}
\displaystyle [{{M}^{0}}{{L}^{1}}{{T}^{{-1}}}]
The phase difference between the waves is
(a) \displaystyle [{{M}^{0}}{{L}^{0}}{{T}^{{-1}}}]
(b) \displaystyle [{{M}^{0}}{{L}^{0}}{{T}^{1}}]
(c) \displaystyle 2.5\times {{10}^{{-4}}}\text{cm}
(d) zero
Ans. (c)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
