Video Lecture
Theory For Notes Making
Basic properties of conductors in electrostatics
It is possible and convenient to classify most materials as conductors or insulators according to their ability to conduct electricity. In an insulator such as rubber or glass, the electronsare attached to their atoms and can not break free even if there is and external electric field. On the other hand , in metallic conductors, one or more electrons per atom are free to move about through the material and can be used for conduction purpose . Theoretically a perfect conductor is a material which haveunlimitednumber of completely free electrons. In real life situations, there are no perfect conductors, but many substances come quite close. Conductors have their unique properties in electrostatic equilibrium conditions (when all charges of conductor are at rest) . Let’s discuss them one by one
1.
Electric field is zero inside a conductor
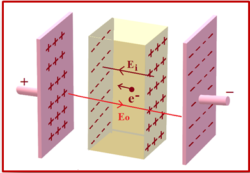
Suppose we put a metallic slab into an external field \displaystyle {{\vec{E}}_{0}} Initially, this will drive any positive charge towards right and negative one to the left (Actually, it is only negative charges (electrons) that move but when they move towards left, positive charge (stationary protons) are left on the right side),
When they pile up on the edge of the material plus on the right side and negative on left side, they produce an electric field \displaystyle {{\vec{E}}_{i}} in opposite direction to \displaystyle {{\vec{E}}_{0}} . The net field inside the conductor is now \displaystyle {{\vec{E}}_{0}}-{{\vec{E}}_{i}} . This field will again drive charges by exerting force on the charges. Let the force be \displaystyle {{\vec{F}}_{i}} which is given by
\displaystyle {{\vec{F}}_{i}}=-({{\vec{E}}_{0}}-{{\vec{E}}_{i}})e, Due to this force the charges continues to move and hence the surface charges on the conductor goes on increasing. As a result the electric field \displaystyle {{\vec{E}}_{i}} also increases. But due to this the net electric field \displaystyle ({{\vec{E}}_{0}}-{{\vec{E}}_{i}}) in the conductor start decreasing and finally becomes zero. At that moment the force acting on the charge will also become zero and charges stops moving. This is called electrostatic equilibrium. Hence in electrostatic equilibrium the net electric field inside the conductor is always zero.
2.
Excess charges always lie on the surface
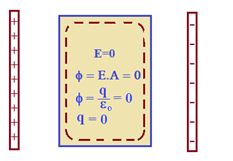
This follows from Gauss law. If we imagine any closed gaussian surface which is just inside the surface, the electric flux through the surface is zero as there is no electric field inside the conductor, and hence net charge enclosed must be zero. Therefore any excess charge must reside on the surface.
3.
Potential is constant inside the conductor
If `a’ and `b’ are any two points within a given conductor
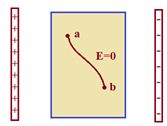
Then \displaystyle {{V}_{b}}-{{V}_{a}}=-\int\limits_{a}^{b}{{\vec{E}.d\vec{l}}}
but E = 0 inside the conductor therefore \displaystyle {{V}_{b}}-{{V}_{a}}=0
and hence Vb = Va.
4.
Electric field is perpendicular to the surface, just outside the conductor.
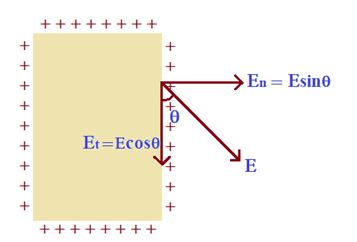
Consider if Electric field `E’ would have made an angle q with the surface. In that case it can be resolved into two components En (normal to the surface) and Et (along the surface). Consider a charge q on the surface. It will experience two forces Fn = Enq and Ft=Etq due to these two components. Since charge can not flow perpendicular to the surface since it is confined to the conductorso Fncan not produce motion in the charges but charge will immediately flow around the surface due to the tangential force Ft.That Produces a surface current, but as the conductor finally comes to electrostatic equilibrium hence all charges must come to rest, which is possible only when Ft force is zero.
As Ft=Et.q = 0 therefore Et = 0.
hence E cosθ = 0 or cosθ = 0 ( As E cannot be zero out the charged conductor)
this finally gives θ=90o. So we conclude that the net electric field just outside the conductor should be normal to the surface of conductor
If σ is the surface charge density at a point on the surface Gauss law can be used to show that \displaystyle {{\vec{E}}_{\bot }}=\frac{\sigma }{{{{\varepsilon }_{0}}}}
5.
The charge density tends to be higher on isolated conducting surfaces whose radii of curvature are smaller and vice-versa. For instance, the charge density tends to be relatively high on sharp edges and corners and relatively low on plane surfaces on a conducting body.
Proof : As a conductor is an equipotential VS= constt. In case of spherical conductor,
{{V}_{S}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{q}{R} with q= 4πR2σ
So {{V}_{S}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{4\pi {{R}^{2}}\sigma }}{R}= constt.,
⇒ σR = constt.
⇒σ ∝ (1/R)
This is the reason why lightning rods are made sharply pointed at the top. These rods help protecting tall buildings from lightning by conducting the charge of the cloud to the ground.
Since the electric field is proportional to the charged density for points which are just above the charged surface, electric field reaches very high values near sharp edges and corners. This is technically very important, because air will break down if the electric field is too high. What happens is that a loose charge (electron, ion) somewhere in air will be accelerated by the field and if the field is large, the charge can pick up enough speed before it hits another atom to be able to knock an electron off atom. As a result, more and more ions are produced. Their motion constitutes a discharge or spark. This will result in discharging the conductor. During thunder storms, glow discharges near sharp points are a common sight.
Proof : As a conductor is an equipotential VS= constt. In case of spherical conductor,
{{V}_{S}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{q}{R} with q= 4πR2σ
So {{V}_{S}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{4\pi {{R}^{2}}\sigma }}{R} = constt.,
⇒ σR = constt.
⇒ σ ∝ (1/R)
This is the reason why lightning rods are made sharply pointed at the top. These rods help protecting tall buildings from lightning by conducting the charge of the cloud to the ground.
Force Acting on the Surface of a charged Conductor (Electrostatic Pressure)
When a conductor is placed into an electric field, or when a certain charge is imported to it, charges appear on the surface of the conductor. The surface charge density s may or may not be same everywhere on the surface.
Consider a small section of the conductor near its surface. The force on small area element ΔS on the surface is
\displaystyle \Delta \vec{F}=\sigma \Delta S{{\vec{E}}_{0}} …(i)
wheres ΔS is the charge of this element and \displaystyle {{\vec{E}}_{0}} is the field created by all other charges of the system.
Note that \displaystyle {{\vec{E}}_{0}} is not equal to the net field intensity \displaystyle {\vec{E}} existing in the vicinity of the surface element.
Let \displaystyle {{\vec{E}}_{\sigma }} = the intensity of the field created by the charge of area element ΔS.
\displaystyle {{\vec{E}}_{0}} = the intensity of the field created by all the other charges of the system
and \displaystyle \vec{E}= the intensity of the resultant field when the fields {{\vec{E}}_{\sigma }} and \displaystyle {{\vec{E}}_{0}} are superimposed.
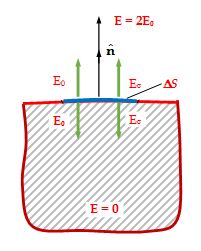
At the points very close to area element, it behaves as an element, it behaves as an infinite uniformly charged plane. Hence,
{{E}_{\sigma }}\text{ }=\text{ }\frac{\sigma }{{\text{2}{{\varepsilon }_{0}}}}
on the two sides of the area element, Es has opposite directions; but E0 has same direction.
Inside the conductor, \displaystyle \vec{E}, Es = E0. Therefore, outside the conductor,
E = E0 + Eσ = 2E0.
Thus, Eqn. (i) becomes \displaystyle \Delta \vec{F}=\frac{1}{2}\sigma (\Delta S)\vec{E} …(ii)
Dividing both sides by ΔS, we obtain the force acting on unit surface, called surface density of force or electrostatic pressure (P)
\displaystyle P=\frac{{\left| {\Delta \vec{F}} \right|}}{{\Delta S}}=\frac{1}{2}\sigma E Since \displaystyle E=\frac{\sigma }{{{{\varepsilon }_{o}}}} , at any point just outside the surface,
we have \displaystyle P=\frac{{{{\sigma }^{2}}}}{{2{{\varepsilon }_{o}}}} or \displaystyle P=\frac{1}{2}{{\varepsilon }_{o}}{{E}^{2}}
Note that regardless of the sign of s the electrostatic pressure is always directed outward the conductor. That is, the pressure tends to stretch the conductor. And that is why a soap bubble always expends irrespective of the type of charge (positive or negative) given to it.
Induced charge and Electrostatic shielding.
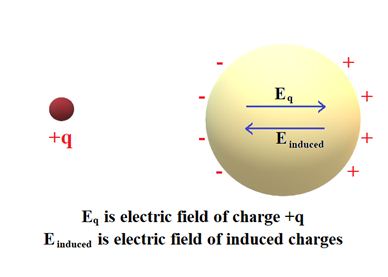
If a point charge q is brought near an uncharged conductor, charge q pulls minus charges over to near side and repel plus charge to the far side. (Alternate way to think of this is that the free charge move in such a way so as to cancel off the field due to q at points inside the conductor where the total field must be zero). Since negative charge is closer to q , there is net force of attraction between the charge q and the conductor
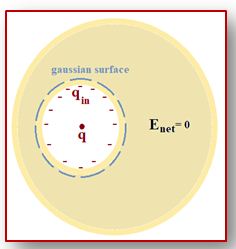
If there is a cavity inside a conductor and if there is a charge q inside the cavity, then the field inside the cavity is non-zero. But in a remarkable way, cavity and its contents are electrically isolated from the outside world by the surrounding conductor. The field due to charge q within the cavity is cancelled, for all exterior points, by the induced charge on the inner surface of the cavity.
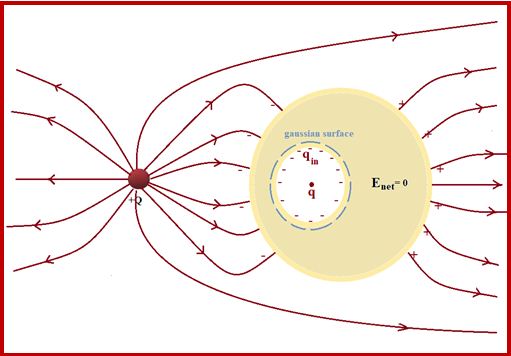
The total charge induced on the cavity wall is equal and opposite to charge inside. This follows from gauss law
We know that \displaystyle \oint\limits_{s}{{\vec{E}.d\vec{S}=\frac{{{{q}_{{enclosed}}}}}{{{{\varepsilon }_{o}}}}}} but E is zero inside the meat of the conductor hence the LHS of this equation becomes zero. and therefore qenclosed = 0. Now there are two charges inside the gaussian surface i.e. q (That is placed within the cavity) and qinduced (on the inner surface of the cavity).
Thus \displaystyle {{q}_{{enclosed}}}=q+{{q}_{{induced}}}
\displaystyle \Rightarrow \text{ }0=q+{{q}_{{induced}}}
\displaystyle \therefore \text{ }{{q}_{{induced}}}=-q
Similarly, no external field due the outside charges can penetrate the conductor. They are cancelled at the outer surface by the induced charge there.
Illustration
Find the potential of an uncharged conducting sphere provided that a point charge q is located at a distance r from its centre.
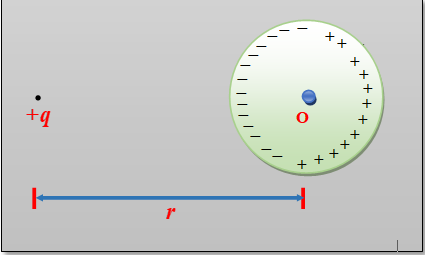
Since potential V is the same for all points of the sphere. Therefore, we can calculate its value at the centreO of the sphere, because only for this point it can be calculated in the most simple way:
V = \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{q}{r}\,+V’ (i)
where V’ shows the potential of the point O due to induced charges. Since all induced charges are at the same distance R from the point O and the total induced charge is equals to zero, therefore V’= 0
Hence potential of the sphere is given by V = \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{q}{r}\,
Illustration
A point charge q is within an electrically neutral shell whose outer surface has spherical shape. Find the potential V at the point P lying outside the shell at a distance r from the centreO of the outer surface.
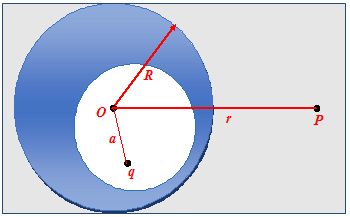
Solution
The field at the point P is determined only by charges induced on the outer spherical surface since the field of the point charge q and of the charges induced on the inner surface of the sphere is equal to zero everywhere outside the cavity.
Next, in view of symmetry, the charge on the outer surface of the shell is distributed uniformly, and
Hence V = \frac{1}{{4\pi {{\varepsilon }_{o}}}}\,\frac{q}{r}.
Equilibrium of Charged Soap Bubble
(1)
For a charged soap bubble of radius R and surface tension T and charge density \sigma . The pressure due to surface tension 4\frac{T}{R} and atmospheric pressure {{P}_{{\text{out}}}} act radially inwards and the electrical pressure ({{P}_{{el}}}) acts radially outward.
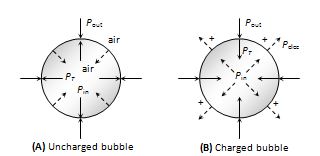
(2)
The total pressure inside the soap bubble
{{P}_{{\text{in}}}}={{P}_{{\text{out}}}}+\frac{{4T}}{R}-\frac{{{{\sigma }^{2}}}}{{2{{\varepsilon }_{0}}}}
(3)
Excess pressure inside the charged soap bubble
{{P}_{{\text{in}}}}-{{P}_{{\text{out}}}}\,\,={{P}_{{\text{excess}}}}=\frac{{4T}}{R}-\frac{{{{\sigma }^{2}}}}{{2{{\varepsilon }_{0}}}}
(4)
If air pressure inside and outside are assumed equal then {{P}_{{\text{in}}}}={{P}_{{\text{out}}}} i.e., {{P}_{{\text{excess}}}}=0 . So, \frac{{4T}}{R}=\frac{{{{\sigma }^{2}}}}{{2{{\varepsilon }_{0}}}}
(i) Charge density : Since \frac{{4T}}{R}=\frac{{{{\sigma }^{2}}}}{{2{{\varepsilon }_{0}}}}
⇒ \sigma \,=\sqrt{{\frac{{8{{\varepsilon }_{0}}T}}{R}}}=\sqrt{{\frac{{2T}}{{\pi kR}}}}
(ii)Radius of bubble R=\frac{{8\,{{\varepsilon }_{0}}\,T}}{{{{\sigma }^{2}}}}
(iii) Surface tension T=\frac{{{{\sigma }^{2}}R}}{{8{{\varepsilon }_{0}}}}
(iv) Total charge on the bubble Q=8\pi R\sqrt{{2{{\varepsilon }_{0}}TR}}
(v) Electric field intensity at the surface of the bubble
E=\sqrt{{\frac{{8T}}{{{{\varepsilon }_{0}}R}}}}=\sqrt{{\frac{{32\pi \,kT}}{R}}}
(vi) Electric potential at the surface V=\sqrt{{32\pi RTk}}=\sqrt{{\frac{{8RT}}{{{{\varepsilon }_{0}}}}}}
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Advance Level)
Q.1
Find the electrostatic force of interaction between two halves of a spherical conductor of radius R carrying a charge Q .
(a) \displaystyle \frac{{{{Q}^{2}}}}{{36\pi {{\varepsilon }_{0}}R}}
(b) \displaystyle \frac{{{{Q}^{5}}}}{{32\pi {{\varepsilon }_{0}}R}}
(c) \displaystyle \frac{{{{Q}^{2}}}}{{32\pi {{\varepsilon }_{0}}R}}
(d) \displaystyle \frac{{{{Q}^{3}}}}{{25\pi {{\varepsilon }_{0}}R}}
Ans. (c)
Q.2
The maximum surface charge density of a uniformly charged spherical conductor of radius R and wall thickness ‘t’, so that it will not burst apart, is
(a) \sqrt{{\frac{{{{\sigma }_{m}}{{\varepsilon }_{0}}t}}{R}}}
(b) \sqrt{{\frac{{2{{\sigma }_{m}}{{\varepsilon }_{0}}t}}{R}}}
(c) \sqrt{{\frac{{3{{\sigma }_{m}}{{\varepsilon }_{0}}t}}{R}}}
(d) \sqrt{{\frac{{4{{\sigma }_{m}}{{\varepsilon }_{0}}t}}{R}}}
Ans. (d)
Q.3
A positive point charge Q is place at a point P, which is at a distance L from the center ‘C” of an uncharged metallic ball of radius There is a point G on the line PC, at a distance R/2 from C. Then, the electric potential at G is
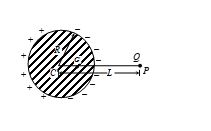
(a) \frac{Q}{{4\pi {{\varepsilon }_{0}}L}}
(b) \frac{Q}{{4\pi {{\varepsilon }_{0}}}}\times \left( {\frac{1}{L}-\frac{1}{R}} \right)
(c) \frac{Q}{{4\pi {{\varepsilon }_{0}}}}\times \left( {\frac{1}{L}-\frac{2}{R}} \right)
(d) none of these
Ans. (a)
4.
A solid sphere of radius R, and dielectric constant k has spherical cavity of radius R/4. A point charge q1 is placed in the cavity. Another charge q2 is placed outside the sphere at a distance of r from q1. Then Coulombic force of interaction between them is found to be ‘F1’. When the same charges are separated by same distance in vacuum then the force of interaction between them is found to be F2, then
(a) {{F}_{1}}=\frac{{{{F}_{2}}}}{k}
(b) {{F}_{2}}=\frac{{{{F}_{1}}}}{k}
(c) {{F}_{1}}\cdot {{F}_{2}}=\frac{1}{k}
(d) {{F}_{1}}={{F}_{2}}
Ans (d)
