Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
Q.1
A ray of light falls normally on a refracting face of a prism of refractive index 1.5. If the ray just fails to emerge from the prism. Then the angle of prism is
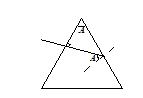
(a) {{\sin }^{{-1}}}\left( {\frac{2}{3}} \right)
(b) {{\cos }^{{-1}}}\left( {\frac{2}{3}} \right)
(c) {{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)
(d) {{\sin }^{{-1}}}\left( {\frac{1}{2}} \right)
Ans. (a)
Q.2
A glass prism of refractive index 1.5 is immersed in water (m = 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, if
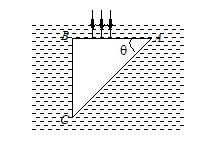
(a) \sin \theta \ge \frac{8}{9}
(b) \sin \theta \le \frac{2}{3}
(c) \sin \theta =\frac{4}{5}
(d) \frac{2}{3}<\sin \theta <\frac{8}{9}
Ans. (a)
Q.3
Light is incident normally on face AB of a prism as shown in figure. A liquid of refractive index m is placed on face AC of the prism. The prism is made of glass of refractive index 3/2. The limits of m for which total internal reflection cannot takes place on face AC is
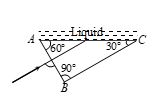
(a) \frac{{3\sqrt{3}}}{4}> m > \frac{{3\sqrt{3}}}{4}
(b) \mu <\frac{{3\sqrt{3}}}{4}
(c) \mu >\sqrt{3}
(d) \mu <\frac{{\sqrt{3}}}{2}
Ans. (b)
Q.4
A ray of light falls on a prism ABC (AB = BC) and travels as shown in figure. The refractive index of the prism material should be greater than
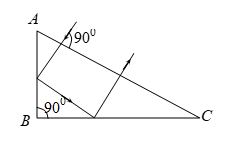
(a) 4/3
(b) \sqrt{2}
(c) 1.5
(d) \sqrt{3}
Ans. (b)
Q.5
We have two equilateral prisms A and B. They are made of materials having refractive index 1.5 and 1.6. For minimum deviation, incident angle will be
(a) small for prism A
(b) small for prism B
(c) equal for both the prisms
(d) can’t be predicted
Ans. (a)
Q.6
A light ray is incident upon a prism in minimum deviation position and suffers a deviation of 34°. If the shaded half of the prism is knocked off, the ray will
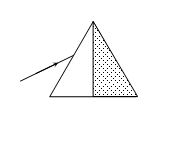
(a) Suffer a deviation of 34°
(b) Suffer a deviation of 68°
(c) Suffer a deviation of 17°
(d) Not come out of the prism
Ans. (c)
Q.7
The light ray is incident at angle of 60° on a prism of angle 45°. When the light ray falls on the other surface at 90°, the refractive index of the material of prism m and the angle of deviation d are given by
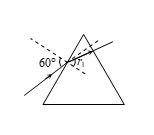
(a) \mu =\sqrt{{\frac{3}{2}}},\,\,\delta =30{}^\circ
(b) \mu =1.5,\,\,\delta =15{}^\circ
(c) \mu =\frac{{\sqrt{3}}}{2},\,\,\delta =30{}^\circ
(d) \mu =\sqrt{{\frac{3}{2}}},\,\delta =15{}^\circ
Ans. (d)
Q.8
For a material, the refractive indices for red, violet and yellow colour light are respectively 1.52, 1.64 and 1.60. The dispersive power of the material is
(a) 2 (b) 0.45 (c) 0.2 (d) 0.045
Ans. (c)
Q.9
A prism (m = 1.5) has a refracting angle of 30°. The deviation of a monochromatic ray incident normally on its one surface will be (sin48°36¢ = 0.75)
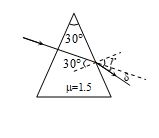
(a) 18°36¢ (b) 22°38¢ (c) 18° (d) 22°1
Ans. (a)
Practice Questions (Level-2)
Q.1
A ray of light makes normal incidence on the diagonal face of a right-angled prism as shown in figure. If \displaystyle \theta = 37o then the angle of deviation is (sin 37o = 3/5)
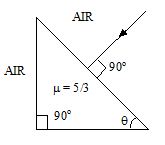
(a) 53o
(b) 127o
(c) 106o
(d) 90o
Ans (c)
Q.2
\displaystyle \eta number of identical equilateral prisms are kept in contact as shown in figure. If deviation through a single prism is \displaystyle \delta then consider the following statements (m is an integer).

(i) if ( \displaystyle \eta = 2m) deviation through \displaystyle \eta prisms is zero
(ii) if ( \displaystyle \eta = 2m +1) deviation through system of \displaystyle \eta prisms is \displaystyle \delta
(iii) if \displaystyle \eta = 2m deviation through system of \displaystyle \eta prisms is \displaystyle \delta
(iv) if \displaystyle \eta = 2m + 1 deviation through system of \displaystyle \eta prisms is zero
(a) statements (i) & (iii) are true
(b) statements (i) and (ii) are true
(c) statements (i) and (iv) are true
(d) statements (iii) and (iv) are true
Ans (b)
Q.3
Two parallel light rays pass through an isosceles prism of refractive index \sqrt{{3/2}} as shown in figure. The angle between the two emergent rays is
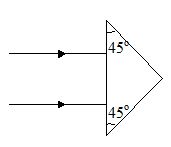
(a) 15o
(b) 30o
(c) 45o
(d) 60o
Ans (b)
Q.4
What is the minimum value of the refractive index for a 90º – 45º – 45º prism which is used to deviate a beam through 90º by total internal reflection?
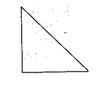
(a) 3/2
(b) \displaystyle \sqrt{3}
(c) \displaystyle \sqrt{2}
(d) 5/3
Ans (c)
Q.5
Light is incident normally on face AB of a prism as shown in figure. A liquid of refractive index \displaystyle \mu is placed on face AC of the prism. The prism is made of glass of refractive index 3/2. The limits of \displaystyle \pi for which total internal reflection takes place on face AC is
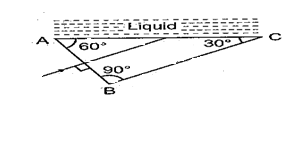
(a) \displaystyle \mu \,>\,\frac{{\sqrt{3}}}{2}
(b) \displaystyle \mu \,<\,\frac{{3\sqrt{3}}}{4}
(c) \displaystyle \mu \,<\sqrt{3}
(d) \displaystyle \mu \,<\frac{{\sqrt{3}}}{2}
Ans (b)
Q.6
A prism having refractive index \sqrt{2} and refracting angle 30o, has one of the refracting surfaces polished. A beam of light incident on the other refracting surface will trace its path if the angle of incidence is
(a) 0o (b) 30o (c) 45o (d) 60o
Ans. (c)
Q.7
A ray of light is incident at an angle i on one surface of a prism of small angle A and emerges normally from the opposite surface. If the refractive index of the material of the prism is m, the angle of incidence i is nearly equal to
(a) \frac{A}{\mu }
(b) \frac{A}{{2\mu }}
(c) mA
(d) \frac{{\mu A}}{2}
Ans. (c)
Q.8
The angle of a prism is A. Its one surface is silvered. Light rays falling at an angle of incidence 2A on first surface retrace the same path after suffering reflection at the second silvered surface. The refractive index of material is
(a) 2 sin A (b) 2 cos A (c) (1/2) cos A (d) tan A
Ans. (b)
Q.9
A thin prism P1 with angle 4° and made from glass of refractive index of 1.54 is combined with another thin prism P2 made from glass of refractive index 1.72 to produce dispersion without deviation. The angle of the prism P2 is
(a) 5.33° (b) 4° (c) 3° (d) 2.6°
Ans. (c)
Q.10
A prism can have a maximum refracting angle of (C = critical angle
(a) 60o (b) C (c) 2C (d) slightly less than 180o]
Ans. (c)
11.
A ray is incident perpendicular to one face of an equilateral prism as in figure. What is the minimum value of the refractive index required for total internal reflection at the second face?
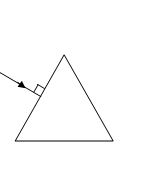
(a) 1.15
(b) 3.0
(c) 1.0
(d) 2.0
Ans (a)
