Video Lecture
Theory For Making Notes
Potential Due to a Continuous Charge Distribution
The potential due to a continuous charge distribution may be obtained by integration.
First find the potential at the given point (see figure) due to an infinitesimally small point
charge dq.
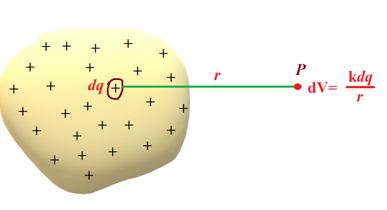
That is dV = \frac{{kdq}}{r}
Now integrate this expression over the whole charge distribution
V = k \int{{\frac{{dq}}{r}}}
Potential due to a uniformly charged ring on its axis
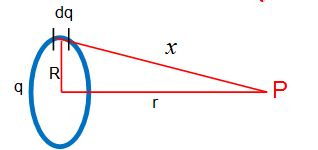
Consider a charge element dq,.Its potential at P is dV where \displaystyle dV=\frac{{kdq}}{x}
Here \displaystyle \text{ }x=\sqrt{{{{R}^{2}}+{{r}^{2}}}} and \displaystyle k=\frac{1}{{4\pi {{\varepsilon }_{o}}}}
\displaystyle \begin{array}{l}\Rightarrow V=-\frac{{KQ}}{R}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}\\\end{array}
Hence dV = \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{dq}}{{\sqrt{{{{r}^{2}}+{{R}^{2}}}}}} now integrate it to get the total potential V
V = ∫dV = \frac{1}{{4\pi {{\varepsilon }_{0}}\sqrt{{{{r}^{2}}+{{R}^{2}}}}}}∫dq
V = \frac{q}{{4\pi {{\varepsilon }_{0}}\sqrt{{{{r}^{2}}+{{R}^{2}}}}}}
Potential due to a uniformly charged disc
Let the charge on the disc = q, and surface charge density is s = \frac{q}{{\pi {{R}^{2}}}}
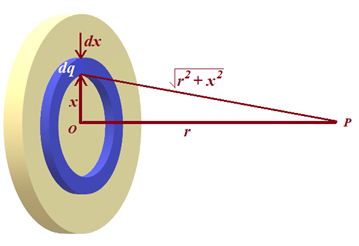
Consider a ring element of radius x and thickness dx. Let the charge on the ring is dq. and the area of the ring is = 2πxdx.
We know that \sigma =\frac{{dq}}{{da}} hence dq=\sigma da=\sigma .2\pi xdx.
Let dV be the potential due to this ring on its axis at point P.
dV=\frac{{kdq}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}}
\displaystyle \Rightarrow dV=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{{\sigma (2\pi xdx)}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}} on integrating we get total potential due to whole disc
\displaystyle \Rightarrow V=\int{{dV=\frac{\sigma }{{2{{\in }_{o}}}}\int\limits_{0}^{R}{{\frac{{xdx}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}}}}}}
Now using the method of substitution to solve this integration we get final answer as
\displaystyle V=\frac{\sigma }{{2{{\in }_{o}}}}[\sqrt{{{{R}^{2}}+{{r}^{2}}}}-r]
Potential due to a uniformly charged spherical shell
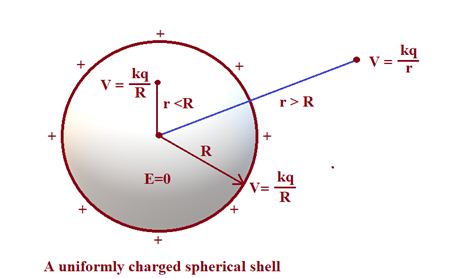
Let the charge on the shell is q. We know that outside the shell
i.e. For r > R, \displaystyle E=\frac{{kq}}{{{{r}^{2}}}}
Also since E = – \frac{{dV}}{{dr}}
Therefore \displaystyle \Rightarrow dV=-E\times dr
On integration from \displaystyle \infty to r, we get \displaystyle \text{ }\int\limits_{\infty }^{r}{{dV}}\text{= -}\int\limits_{\infty }^{\text{r}}{{Edr}}
\displaystyle \Rightarrow \text{ }\left[ V \right]_{\infty }^{r}\text{=-}\int\limits_{\infty }^{\text{r}}{{\frac{{\text{Kq}}}{{{{\text{r}}^{\text{2}}}}}dr}}
\displaystyle \Rightarrow \text{ }\left[ {{{V}_{r}}-{{V}_{\infty }}} \right]\text{= -Kq}\int\limits_{\infty }^{\text{r}}{{\frac{{dr}}{{{{\text{r}}^{\text{2}}}}}}}
But conventionally \displaystyle {{V}_{\infty }}=0 hence \displaystyle {{\text{V}}_{r}}\text{= -Kq}\left[ {-\frac{1}{r}} \right]_{\infty }^{r}
\displaystyle \Rightarrow {{\text{V}}_{r}}\text{= Kq}\left[ {\frac{1}{r}-\frac{1}{\infty }} \right]
Hence finally we get \displaystyle {{\text{V}}_{r}}\text{= }\frac{{\text{Kq}}}{r}\text{ where r R}
For potential on the the surface of shell put r = R in the final result obtained ,
hence Vsurface= \displaystyle \frac{{Kq}}{R}
For potential inside the shell i.e. for r < R
We know that inside a uniformly charge spherical shell electric field is zero
In the relation \displaystyle E=-\frac{{dV}}{{dr}} if we put E = 0 we get \displaystyle \frac{{dV}}{{dr}}=0 . This shows that V is constant in side the shell. Hence the potential varies out side the shell till the surface where the potential becomes maximum and is given by Vsurface= \displaystyle \frac{{Kq}}{R}. Then inside it remain equal to that on the surface as the electric field vanishes as we enter the shell.
So we conclude that Vinside = Vsurface= \displaystyle \frac{{Kq}}{R}.
Note : Remember that where the electric field is zero the potential may be zero or nonzero but it must be constant .
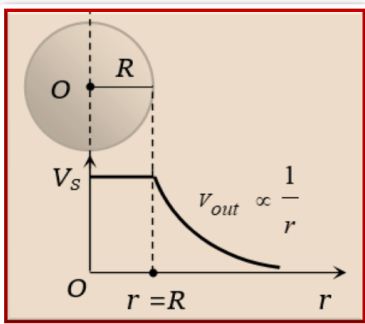
The diagram shows the variation of potential due to a uniformly charged spherical shell.
Potential due to uniformly charged non conducting solid spherical volume
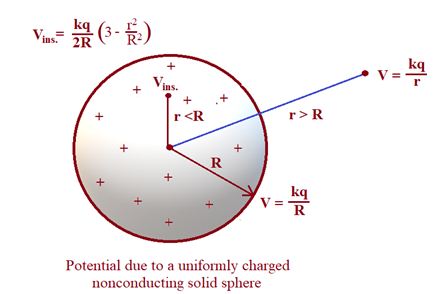
Let the charge in the spherical volume is q and distributed uniformly.
Outside the sphere i.e. For r > R, \displaystyle E=\frac{{kq}}{{{{r}^{2}}}}
Also since E = – \frac{{dV}}{{dr}}
Therefore \displaystyle \Rightarrow dV=-E\times dr
On integration from \displaystyle \infty to r, we get \displaystyle \text{ }\int\limits_{\infty }^{r}{{dV}}\text{= -}\int\limits_{\infty }^{\text{r}}{{Edr}}
\displaystyle \Rightarrow \text{ }\left[ V \right]_{\infty }^{r}\text{=-}\int\limits_{\infty }^{\text{r}}{{\frac{{\text{Kq}}}{{{{\text{r}}^{\text{2}}}}}dr}}
\displaystyle \Rightarrow \text{ }\left[ {{{V}_{r}}-{{V}_{\infty }}} \right]\text{= -Kq}\int\limits_{\infty }^{\text{r}}{{\frac{{dr}}{{{{\text{r}}^{\text{2}}}}}}}
But conventionally \displaystyle {{V}_{\infty }}=0 hence \displaystyle {{\text{V}}_{r}}\text{= -Kq}\left[ {-\frac{1}{r}} \right]_{\infty }^{r}
\displaystyle \Rightarrow {{\text{V}}_{r}}\text{= Kq}\left[ {\frac{1}{r}-\frac{1}{\infty }} \right]
Hence finally we get \displaystyle {{\text{V}}_{r}}\text{= }\frac{{\text{Kq}}}{r}\text{ where r R} (This result is same as that of uniformly charged shell)
For potential on the surface of sphere put r = R in the final result obtained ,
hence Vsurface= \displaystyle \frac{{Kq}}{R} (This result is also same as that of uniformly charged shell)
For potential inside the solid non conducting spherei.e. for r < R
Inside a non conducting solid sphere let the electric field is E
where \displaystyle {{E}_{{in}}}=\frac{{\rho .r}}{{3{{\varepsilon }_{o}}}}=\frac{{Q.r}}{{\frac{4}{3}\pi \text{ }{{\text{R}}^{\text{3}}}\text{.3}{{\varepsilon }_{\text{o}}}}}
\displaystyle \Rightarrow {{E}_{{in}}}=\frac{{Q.r}}{{4\pi {{\varepsilon }_{o}}{{R}^{3}}}}=\frac{{KQ.r}}{{{{R}^{3}}}}
Also we know that outside the non conducting solid sphere the electric field is \displaystyle {{E}_{{out}}}=\frac{{kq}}{{{{r}^{2}}}}
As we know that the potential at any point is the work done to carry a unit positive charge from infinity to that point and is given by the relation \displaystyle \text{ V= -}\int\limits_{\infty }^{\text{r}}{{Edr}} . in this relation E is the electric field between infinity and given point. But in case of solid nonconducting sphere the electric field outside and inside is different so in this case we can define the potential as work done in carrying a unit positive charge from infinity to the surface and then from surface to point inside the sphere.Hence we break the limits of integration as follows
\displaystyle V=-\left[ {\int\limits_{\infty }^{R}{{{{E}_{{out}}}}}dr\text{ + }\int\limits_{\text{R}}^{\text{r}}{{{{\text{E}}_{{in}}}\text{dr}}}} \right]
\displaystyle \Rightarrow V=-\int\limits_{\infty }^{R}{{\frac{{KQ}}{{{{r}^{2}}}}}}\text{ dr }-\text{ }\int\limits_{\text{R}}^{\text{r}}{{\frac{{\text{KQr}}}{{{{\text{R}}^{\text{3}}}}}\text{ dr}}}
\displaystyle \Rightarrow V=-KQ\int\limits_{\infty }^{R}{{\frac{{dr}}{{{{r}^{2}}}}}}\text{ }-\text{ }\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\int\limits_{\text{R}}^{\text{r}}{{\text{r dr}}}
\displaystyle \Rightarrow V=-KQ\left[ {-\frac{1}{r}} \right]_{\infty }^{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\left[ {\frac{{{{r}^{2}}}}{2}} \right]_{R}^{r}
\displaystyle \Rightarrow V=KQ\left[ {\frac{1}{R}-\frac{1}{\infty }} \right]-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\left[ {\frac{{{{r}^{2}}}}{2}-\frac{{{{R}^{2}}}}{2}} \right]
\displaystyle \Rightarrow V=\frac{{KQ}}{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}
\displaystyle \Rightarrow V=\frac{{KQ}}{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}
\displaystyle \Rightarrow V=\frac{{KQ}}{R}\left[ {1-\frac{{{{r}^{2}}}}{{2{{R}^{2}}}}+\frac{1}{2}} \right]
\displaystyle \Rightarrow V=\frac{{\text{KQ}}}{\text{R}}\left[ {\frac{3}{2}-\frac{{{{r}^{2}}}}{{2{{R}^{2}}}}} \right]
\displaystyle \Rightarrow V=\frac{{\text{KQ}}}{{\text{2R}}}\left[ {3-\frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right]
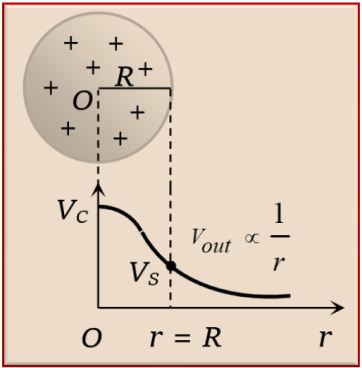
The diagram shows the variation of potential due to a uniformly charged non conducting sphere.
For conducting solid sphere:
(i) (r < R), E = 0, V = \displaystyle \frac{{KQ}}{R}
(ii) (r = R), E = \displaystyle \frac{{KQ}}{{{{R}^{2}}}} , V= \displaystyle \frac{{KQ}}{R}
(iii) (r > R), E = \displaystyle \frac{{KQ}}{{{{r}^{2}}}} , V= \displaystyle \frac{{KQ}}{r}
Illustration
A non-conducting disc of radius ‘a’ and uniform positive surface charge density s is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped along the axis of the disc, from a height H with zero initial velocity. The particle has \frac{q}{m}=\frac{{4{{\varepsilon }_{o}}g}}{\sigma }
(a) Find the value of H the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
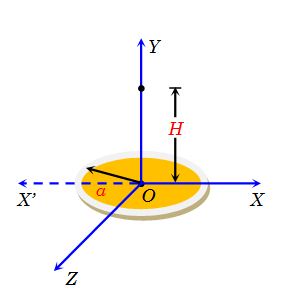
Solution
To solve this problem we use the concept of conservation of mechanical energy as the electric field and gravitational field is conservative in nature. Hence mechanical energy at P= Mechanical energy at O.
mgH+q{{V}_{P}}=q{{V}_{0}}
where {{V}_{P}}= Potential at P due to the disc
= {{V}_{P}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left( {2\pi \sigma } \right)\left[ {\sqrt{{{{H}^{2}}+{{a}^{2}}}}-H} \right]
and {{V}_{0}}= Potential at O due to the disc = {{V}_{0}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}(2\pi \sigma a)
We have taken the reference line X’OX to measure the gravitational potential energy .
mgH = \frac{1}{{4\pi {{\varepsilon }_{0}}}}(2\pi \sigma a) q-\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left( {2\pi \sigma q} \right)\left[ {\sqrt{{{{H}^{2}}+{{a}^{2}}}}-H} \right]
After solving this above equations and using \frac{q}{m}=\frac{{4{{\varepsilon }_{0}}g}}{\sigma } , we get H=\frac{{4a}}{3} .
Note that this problem is solved using force method and work energy theorem.
(b)
Potential energy of particle at height ,
U=\frac{{\sigma q}}{{2{{\varepsilon }_{0}}}}\left[ {\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]+mgy …(i)
Using \frac{q}{m}=\frac{{4{{\varepsilon }_{0}}g}}{\sigma }
U=2mg\left[ {\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]+mgy
U=mg\left[ {2\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]
For equilibrium , \frac{{dU}}{{dy}}=0
mg\left[ {\frac{{2.2{{y}_{0}}}}{{2\sqrt{{{{y}^{2}}+{{a}^{2}}}}}}-1} \right]= 0
{{y}_{0}}=\frac{a}{{\sqrt{3}}}
As \frac{{{{d}^{2}}U}}{{d{{y}^{2}}}}=mg\left[ {\frac{{2\sqrt{{{{y}^{2}}+{{a}^{2}}}}-2y\times \frac{1}{2}{{{({{y}^{2}}+{{a}^{2}})}}^{{-{1}/{2}\;}}}.2y}}{{({{y}^{2}}+{{a}^{2}})}}} \right]
at y={{y}_{0}}\frac{a}{{\sqrt{3}}} is +ve i.e., \frac{{{{d}^{2}}U}}{{d{{y}^{2}}}}>0
for y={{y}_{0}}=\frac{a}{{\sqrt{3}}}.
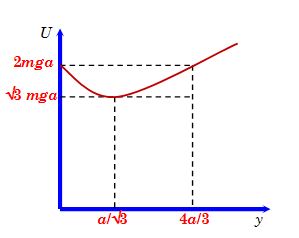
implies that U is minimum at equilibrium.
Umin = \sqrt{3}mga, [Put y=\frac{a}{{\sqrt{3}}} in (i)]
It is interesting at y=\frac{{4a}}{3}, U=2mga
and at y=0, U=2mga.
Potential energy as function of Y is shown in figure.
Potential of concentric conducting spheres: Superposition Principle
Let us consider two spheres of radii r1 and r2 with uniformly distributed charges q1 and q2as shown in the figure .Using the principle of superposition, the potential of the small and large sphere may be written as
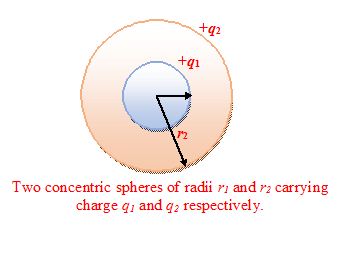
V1 = \frac{{k{{q}_{1}}}}{{{{r}_{1}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}
V2 = \frac{{k{{q}_{1}}}}{{{{r}_{2}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}
Redistribution of Charge

If two conductors are brought into contact, the charges from one of them will flow over to the other until their potentials become equal. The equality of potential implies that charges on each sphere as shown in figure is proportional to its radius
i.e. \frac{{{{q}_{1}}}}{{{{R}_{1}}}}\,\,=\frac{{{{q}_{2}}}}{{{{R}_{2}}}}
For a uniform surface charge density σ, the total charge q = 4πR2σ,so the above equation becomes
\frac{{{{\sigma }_{1}}}}{{{{\sigma }_{2}}}}\,=\frac{{{{R}_{2}}}}{{{{R}_{1}}}}
The surface charge density of each sphere is inversely proportional to the radius.
Illustration
Given two concentric conducting spheres of radii r and R ( r <R)
The inner surface carries a charge qoand the outer sphere is earthed
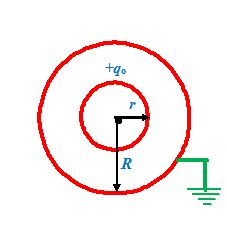
(a) Find the charge on the outer sphere
(b) Find the potential of the inner surface
Solution
(a)
Let q be the final charge on the outer sphere.
Using equation , the potential on the outer sphere is given by
V2 = \frac{{k{{q}_{o}}}}{R}\,+\frac{{kq}}{R}
Since it has been earthed, therefore, V2 = 0
Thus, \frac{{k{{q}_{o}}}}{R}\,+\frac{{kq}}{R} = 0
q = –qo
(b)
The potential of the inner sphere may be obtained using equations
V1 = \frac{{k{{q}_{o}}}}{r}\,-\frac{{k{{q}_{o}}}}{R}
= kqo \left[ {\frac{1}{r}\,-\frac{1}{R}} \right]
Illustration
In the previous example if the outer sphere carries a charge +qo and the inner sphere is earthed, then find
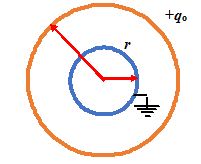
(a) the charge on the inner sphere, and
(b) the potential of the outer sphere.
Solution
(a)
Let q be the charge on the inner sphere.
since it is earthed so its total potential should be zero
hence \frac{{kq}}{r}\,+\frac{{k{{q}_{o}}}}{R}\,=0
Thus q = –qo \frac{r}{R}
(b)
The potential of the outer sphere is given by
V2= \frac{k}{R}\left( {-{{q}_{o}}\frac{r}{R}} \right) + \frac{{k{{q}_{0}}}}{R}
or V2= \frac{{k{{q}_{o}}}}{R}\,\left[ {1\,-\frac{r}{R}} \right]
Practice Questions (Level-1)
1.
Two infinitely long parallel conducting plates having surface charge densities +s and –s respectively, are separated by a small distance `d’. The medium between the plates is vacuum. If e0 is the dielectric permittivity of vacuum, then the potential difference between the plates is
(a) zero (b) \displaystyle \frac{{\sigma d}}{{2{{\varepsilon }_{o}}}}
(c) \displaystyle \frac{{\sigma d}}{{{{\varepsilon }_{o}}}} (d) \displaystyle \frac{{2\sigma d}}{{{{\varepsilon }_{o}}}}
Ans (c)
2.
Two spheres of radii r and R carry charges q and Q respectively. When they are connected by a wire, there will be no loss of energy of the system if
(a) qr = QR
(b) qR = Qr
(c) qr2 = QR2
(d) qR2 = Qr2
Ans (b)
3.
In the figure shown, conducting shells A and B have charges Q and 2Q distributed uniformly over A and B .Value of VA – VB is
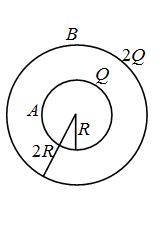
(a) \frac{Q}{{4\pi {{\varepsilon }_{0}}R}}
(b) \frac{Q}{{8\pi {{\varepsilon }_{0}}R}}
(c) \frac{{3Q}}{{4\pi {{\varepsilon }_{0}}R}}
(d) \frac{{3Q}}{{8\pi {{\varepsilon }_{0}}R}}
Ans (b)
4.
A solid conducting sphere of radius 5 cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
(a) 5 V
(b) 10 V
(c) 15 V
(d) zero
Ans (b)
5.
Two concentric conducting shells A and B are of radii R and 2R. A charge q is placed at the centre of shells. Shell B is earthed and a charge q is given to shell A. If charges on outer surface of A and B are QA and QB respectively, then
(a) QA = q, QB = 0 (b) QA = 2q, QB = q
(c) QA = 2q, QB = 0 (d) QA = q, QB = q
Ans (c)
6.
Two spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of
5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surface of spheres A and B is
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 2 : 1
Ans (d)
Practice Questions (Level-2)
1.
Two spheres A and B of radius 4cm and 6cm are given charges of 80mC and 40mC respectively. If they are connected by a fine wire, the amount of charge flowing from one to the other is
(a) 20 \displaystyle \mu C from A to B
(b) 16 \displaystyle \mu C from A to B
(c) 32 \displaystyle \mu C from B to A
(d) 32 \displaystyle \mu C from A to B
Ans (d)
2.
A point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the centre of the shell. The electric potential at the centre of shell will be \frac{1}{{4\pi {{\varepsilon }_{0}}}} times (potential at infinity is zero)
(a) \frac{q}{{2R}}
(b) \frac{{4q}}{{3R}}
(c) \frac{{5q}}{{6R}}
(d) \frac{{2q}}{{3R}}
Ans (c)
3.
A solid hemispherical uniform charged body having charge Q is kept symmetrically along the y-axis as shown in figure. The electric potential at a distance d from the origin along the x-axis at point P will be
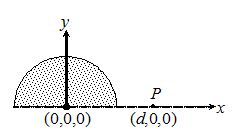
(a) \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{d}
(b) less than \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{d}
(c) more than \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}} and less than \frac{2}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}}
(d) more than \frac{2}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}}
Ans (a)
