Video Lecture
Theory For Making Notes
Optical Instruments
Simple Microscope
A simple convex lens is said to be a simple microscope when the object is placed between focus and optical centre of lens and the eye of the observer is kept close to the lens. The image found in this case will be erect and enlarged.
Magnifying power [Angular magnification]
For an optical instrument it is defined as the ratio of angle made by image at the eye to the maximum angle made by the object at the eye when placed at least distance of distinct vision (i.e. 25 cm denoted by D)
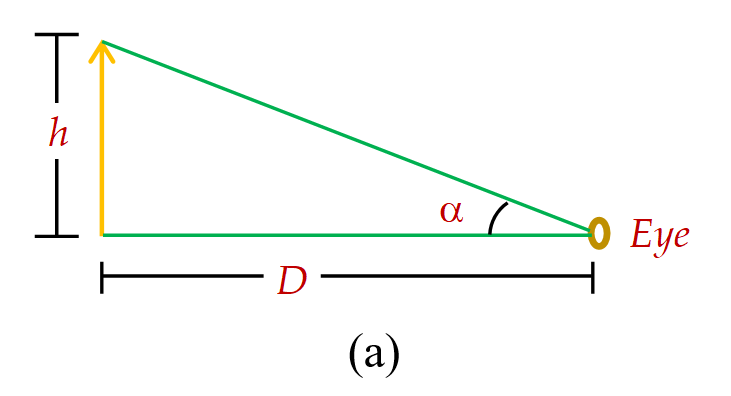
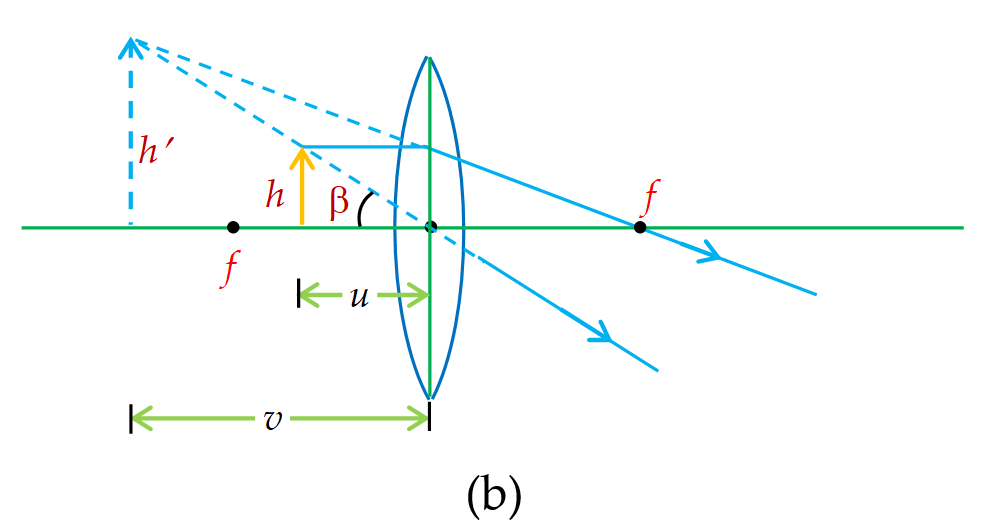
Figure (a) shows an object of height h placed at distance D from the eye of the observer. Let \displaystyle \alpha is the angle made by the object at the eye. Hence \displaystyle \alpha =\frac{h}{D}.
Figure (b) shows the simple microscope where the image of height h’ is making an angle \displaystyle \beta at the optical centre of lens (or eye of the observer) hence \displaystyle \beta =\frac{h}{u}.
Therefore \displaystyle M=\frac{\beta }{\alpha }=\frac{{h\times D}}{{u\times h}}=\frac{D}{u}
If the image is at D [Near point]
In this situation as v = – D, from lens-formula
\displaystyle \frac{1}{v}-\frac{1}{u}=\frac{1}{f}, we have
\displaystyle \frac{1}{{-D}}-\frac{1}{{-u}}=\frac{1}{f},\ \ i.e.,\ \frac{D}{u}=1+\frac{D}{f}
So
\displaystyle MP=\frac{D}{u}=\left[ {1+\frac{D}{f}} \right]
If the image is at infinity [Far point]
In this situation from lens-formula , \displaystyle \frac{1}{v}-\frac{1}{u}=\frac{1}{f}, we have
\displaystyle \frac{1}{\infty }-\frac{1}{{-u}}=\frac{1}{f} i.e., u = f
So \displaystyle \text{MP}=\frac{D}{u}=\frac{D}{f}
As here u is maximum [because the object is to be within focus], MP is minimum and as in this situation parallel beam of light enters the eye, eye is least strained and is said to be normal, relaxed or unstrained.
In this case the magnification \displaystyle \left[ {i.e.\text{ }\frac{D}{f}} \right] is one less than the magnification \displaystyle \left[ {i.e.\text{ }1+\frac{D}{f}} \right] when the image is formed at the near point, but, naturally, viewing is more comfortable and the difference in magnification usually small.
For example, if we want a magnification of six, f required will be 5 cm in the first case (taking D = 25 cm) and (D/6 = 25/6) \displaystyle \simeq 4cm in the second case.
So, magnification is approximately inversely proportional to the focal length smaller the f, smaller will be radius of the sphere out of which the lens is to be cut off. Hence, for all practical purposes, it is not possible to have magnification greater than 10 through a simple microscope. For higher magnifications, we need at least two lenses, one compounding the effect of the other. This is termed as compound microscope.
Compound Microscope
Two lenses are used here, one compounding the effect of the other. The one nearer to the object is called objective. The other nearer to the eye is called eyepiece.
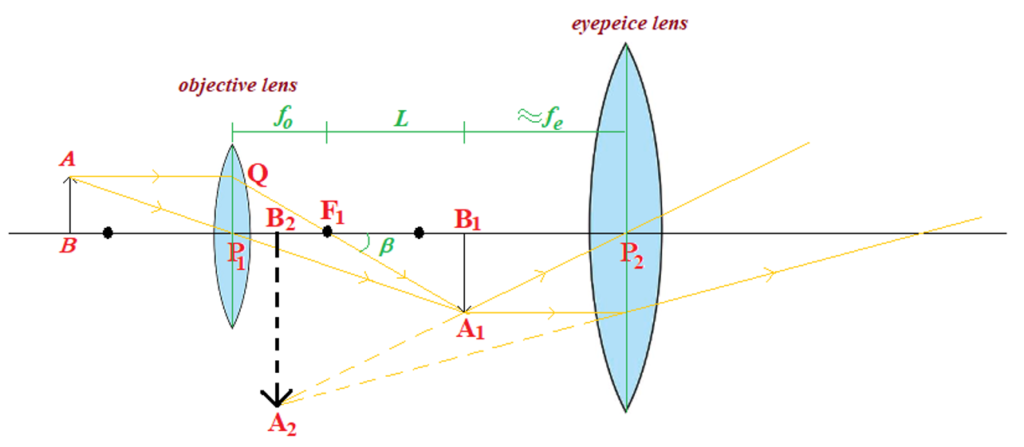
Objective makes a real, inverted, magnified image ( \displaystyle {{A}_{1}}{{B}_{1}}) of the object (AB). This serves as the object for the eyepiece which functions just like a simple microscope or magnifier, producing an enlarged, virtual final image( \displaystyle {{A}_{2}}{{B}_{2}}). The first inverted image would be at the focus of the eyepiece if the eye is focused at \displaystyle \infty , or near the focus of the eyepiece if the eye is to be focused at the near point. Further, the final image is inverted with respect to the object.
Magnification of a compound microscope
\displaystyle {{M }_{o}}, linear magnification due to the objective
=\frac{{{{I}_{\mathbf{1}}}}}{O}=\frac{{{{\mathbf{A}}_{\mathbf{1}}}{{\mathbf{B}}_{\mathbf{1}}}}}{{\mathbf{AB}}}
But AB = \displaystyle {{P}_{1}}Q (from the figure)
so {{M}_{o}}=\frac{{{{A}_{1}}{{B}_{1}}}}{{{{P}_{1}}Q}} …(i)
Now \displaystyle \Delta {{P}_{1}}Q{{F}_{1}} and \displaystyle \Delta {{B}_{1}}{{A}_{1}}{{F}_{1}} are similar,
therefore \displaystyle \frac{{{{A}_{1}}{{B}_{1}}}}{{{{B}_{1}}{{F}_{1}}}}=\frac{{{{P}_{1}}Q}}{{{{P}_{1}}{{F}_{1}}}}
or \displaystyle \frac{{{{A}_{1}}{{B}_{1}}}}{{{{P}_{1}}Q}}=\frac{{{{B}_{1}}{{F}_{1}}}}{{{{P}_{1}}{{F}_{1}}}}=\frac{L}{{{{f}_{o}}}} …(ii)
from (ii) and (i) we get
{{M}_{0}}=\frac{L}{{{{f}_{0}}}} …(iii)
Now, let the eye is focused at \displaystyle \infty . This means \displaystyle {{A}_{1}}{{B}_{1}} (the image by objective) is made at the focus of the eyepiece. Angular magnification by eyepiece (i.e., a simple microscope, as already dealt with), \displaystyle {{M}_{e}} will thus be
{{M}_{e}}=\frac{D}{{{{f}_{e}}}} …(iv)
therefore total magnification, M={{M}_{0}}\times {{M}_{e}}
or {M=\frac{L}{{{{f}_{0}}}}\times \frac{D}{{{{f}_{e}}}}}
Where, for all practical purposes L is approximately equal to the length of the compound microscope, and D = 25 cm; and \displaystyle {{f}_{o}} and \displaystyle {{f}_{e}} are the focal lengths of the objective and eyepiece respectively.
If the eye is focused at near point, \displaystyle {{M}_{e}} will be (as already derived in case of a simple microscope) =\left( {1+\frac{D}{{{{f}_{e}}}}} \right).
Therefore the total magnification will become, {M=\frac{L}{{{{f}_{0}}}}\times \left( {1+\frac{D}{{{{f}_{e}}}}} \right)} .
Note:
- In the above formulas of magnification, only numerical values of L, D, \displaystyle {{f}_{o}} and \displaystyle {{f}_{e}} are to be substituted.
- Modern compound microscopes, however, are not as simple as the one we have dealt with. The principle, however, remains the same. In modern microscope, both the objective and eyepiece themselves are made up of sets of many component lenses. Magnifications upto 1000 are possible with modern microscopes.
- As the aperture of both the lenses in a microscope is small, the defects of images particularly spherical aberration is minimum.
- As MP for normal setting is ( \displaystyle LD/{{f}_{0}}{{f}_{e}}), so to have large MP, \displaystyle {{f}_{o}} and \displaystyle {{f}_{e}} must be as small as practically possible. This is why in a microscope both the lenses have small focal lengths.
- Out of \displaystyle {{f}_{o}} and \displaystyle {{f}_{e}}, \displaystyle {{f}_{o}}is taken to be smaller, so that field of view may be increased and objective being closer to object may collect more light to increase brightness of the image. This also makes sure that intermediate image is in front of eye lens within its focus.
Telescopes
Telescope is used to provide angular magnification to distant objects. In other words a telescope is an optical instrument to clearly observe the distant object.
Types of Telescopes
Telescopes are basically of two types i.e. refracting and reflecting.
The refractive type telescopes are of two types:
(i) Astronomical telescope
This telescope is used to observe heavenly objects like moon. Distant stars and planets etc. The image formed by this telescope is virtual and inverted. Since the heavenly bodies are almost round, so the inverted images does not affect the observations.
(ii) Terrestrial telescope
This telescope is used to observe the objects on the earth like trees, houses etc. and hence called terrestrial telescope. In this telescope the final image is virtual and erect.
The reflecting telescopes are of two types :
(i) Cassegrain type
(ii) Newtonian type
Principle of Astronomical telescope can be discussed by considering two extreme cases,
(a) Distinct vision (b) Normal vision
Like compound microscope, astronomical telescope also consist of objective and eyepiece. These objective are of large focal length and large apertures. A parallel beam of light rays come from a distant object, enters the objective and a real, inverted image is formed in the tube at the focus of the objective. If the telescope is to be adjusted for near point i.e. the final image to be made by the eyepiece, is to be made at a distance D = 25 cm from the eye (or eyepiece, if the two are close to each other), then the length of the tube is so adjusted that the objective forms the image of the distant object at its own focus and which position should be situated between the focus and its optical centre, as shown in the first sketch of the eyepiece.
If the telescope is to be adjusted for eye focused at \displaystyle \infty (called normal adjustment), then the image made by the objective should be at its own focus as well as at the focus of the eyepiece.
The final image in both cases remains still inverted, However, inversion of image does not matter in case of planets or stars.
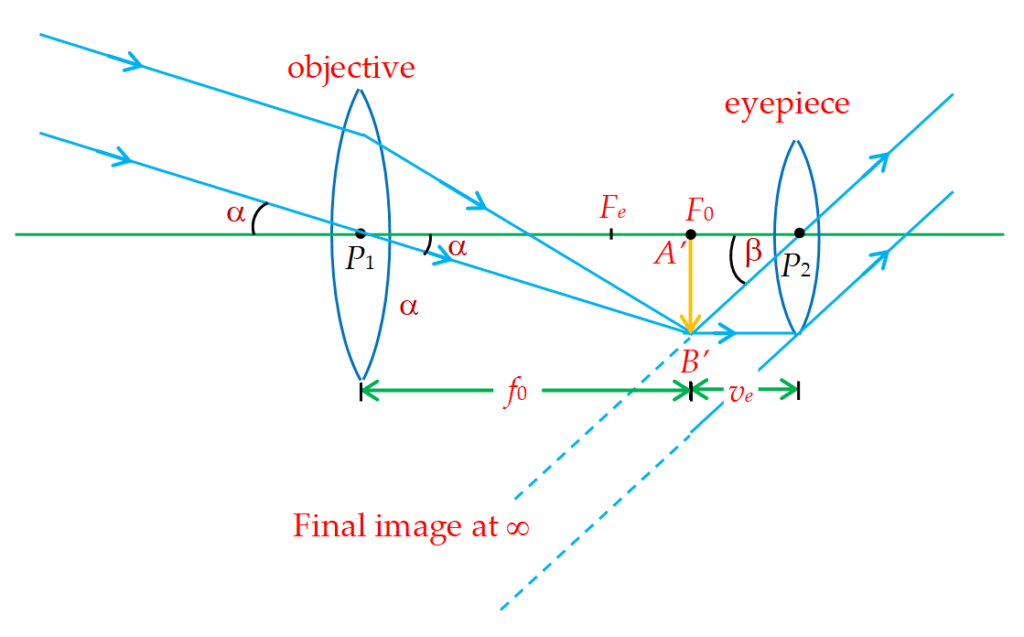
Astonomical refracting type telescope is shown in the diagram given below. The telescope is forming the final image at the least distance of distinct vision (D) from the eyepiece
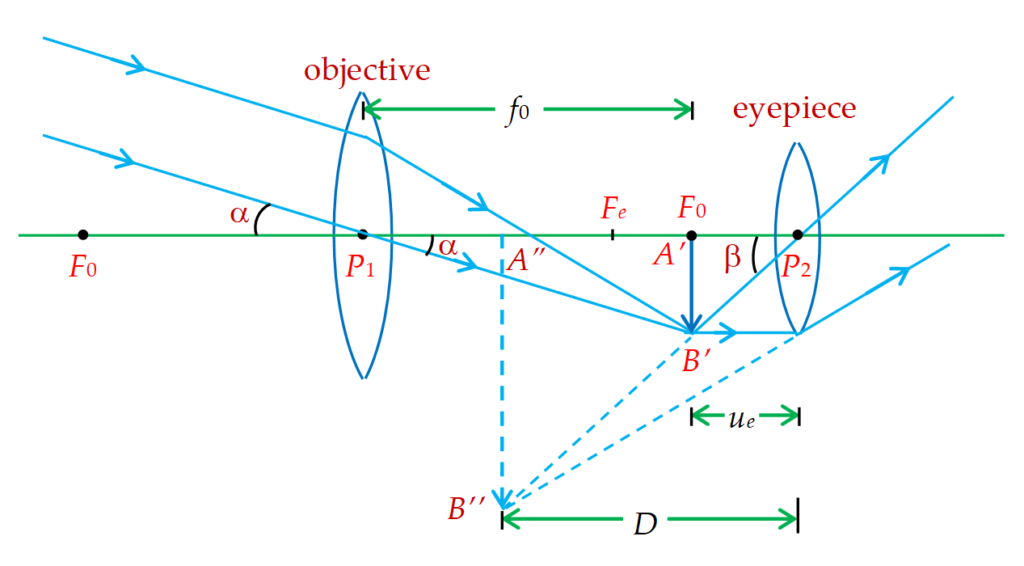
The objective lens is receiving light from a distant object say at infinity and forms a real image it its own focus {{F}_{o}}. This image serves like a real object for the eyepiece. The eyepiece is so placed that its object ( {{A}^{\prime}}{{B}^{\prime}}) falls between the focus {{F}_{e}} and the pole {{P}_{2}} and hence a final virtual image is formed at the least distance of distinct vision (D) from the eyepiece.
Magnifying power (M)
Magnifying power (M), also called angular magnification of a telescope is defined as the ratio of the visual angle ( \displaystyle \beta ) subtended by the final image at the eye and the visual angle ( \displaystyle \alpha ) subtended by the object when the object lies in the actual position.
So, M=\frac{\beta }{\alpha }=\frac{{\tan \beta }}{{\tan \alpha }} ( \alpha,\beta are small)
here \tan \beta =\frac{{{A}'{B}’}}{{{A}'{{P}_{2}}}}
and \displaystyle \tan \alpha =\frac{{{A}'{B}’}}{{{{P}_{1}}{A}’}}
Hence putting value with sign convention in the equation of M, we get
M=\frac{{+{{f}_{0}}}}{{-{{u}_{e}}}}
M=-\frac{{{{f}_{0}}}}{{{{u}_{e}}}} …(i)
This is the general formula for the magnifying power of a telescope.
Magnifying power, if eye is focused at near point
For the eyepiece,
v=-D
u=-{{u}_{e}}
f=+{{f}_{e}}
Where, D = minimum distance of distinct vision
Using lens formula, we get
\frac{1}{v}-\frac{1}{u}=\frac{1}{f}
\frac{1}{{-D}}-\frac{1}{{-{{u}_{e}}}}=\frac{1}{{{{f}_{e}}}}
or \frac{1}{{{{u}_{e}}}}=\frac{1}{{{{f}_{e}}}}+\frac{1}{D} …(ii)
From equation (i) and (ii)
{M=\frac{{-{{f}_{0}}}}{{{{f}_{e}}}}\left( {1+\frac{{{{f}_{e}}}}{D}} \right)} …(iii)
In this case, the length of the telescope is
={{f}_{0}}+{{u}_{e}}
Magnifying power when eye is focused at \displaystyle \infty (normal adjustment)
In this case, as already explained, we have
{{u}_{e}}={{f}_{e}} …(iv)
Again from equation (i) and (iv)
{M=-\frac{{f}_{0}}{{f}_{e}}} …(v)
In this case, the length of the telescope
={{f}_{0}}+{{f}_{e}}
This is the reason why the focal length of objective is taken large and to that of eyepiece is taken small in case of a telescope. This also increases the resolving power of the telescope as we shall see a little while later.
Further, linear or lateral magnification does not convey much meaning in case of a telescope because the size of final images too is negligible compared to actual size of the objects which are generally planets or stars.
Normal vision.
When the final image formed is at infinity, the telescope is said to be in normal adjustment.
The position of the eyepiece is adjusted in a way that the image formed by objective falls on the focus ({{F}_{o}}) of eyepiece and a final image is formed which is real, inverted and highly magnified as shown in figure.
Magnifying power when eye is focused at \displaystyle \infty (normal adjustment)
In this case, as already explained, we have
{{u}_{e}}={{f}_{e}} …(iv)
Again from equation (i) and (iv)
{M=-\frac{{{f}_{0}}}{{{f}_{e}}}} …(v)
In this case, the length of the telescope ={{f}_{0}}+{{f}_{e}}
This is the reason why the focal length of objective is taken large and to that of eyepiece is taken small in case of a telescope. This also increases the resolving power of the telescope as we shall see a little while later.
Further, linear or lateral magnification does not convey much meaning in case of a telescope because the size of final images too is negligible compared to actual size of the objects which are generally planets or stars.
Note:
(i)
For given telescope, magnifying power is minimum when final image is at infinity (far point) and maximum when it is at least distance of distinct vision (Near point), i.e.,
\displaystyle (MP)min=-\left[ {\frac{{{{f}_{0}}}}{{{{f}_{e}}}}} \right]
And \displaystyle (MP)max=-\frac{{{{f}_{0}}}}{{{{f}_{e}}}}\left[ {1+\frac{{{{f}_{e}}}}{D}} \right]
(ii)
In a telescope, if field and eye lenses are interchanged MP will change from ( \displaystyle {{f}_{o}}/{{f}_{e}}) to ( \displaystyle {{f}_{e}}/{{f}_{o}}), i.e., it will change from m to (1/m) i.e., will become ( \displaystyle 1/{{m}^{2}}) times of its initial value.
(iii)
As MP for normal setting as ( \displaystyle {{f}_{o}}/{{f}_{e}}), so to have large MP, \displaystyle {{f}_{o}} must be as large as practically possible and \displaystyle {{f}_{e}} small.
Refracting type telescope (Terrestrial)
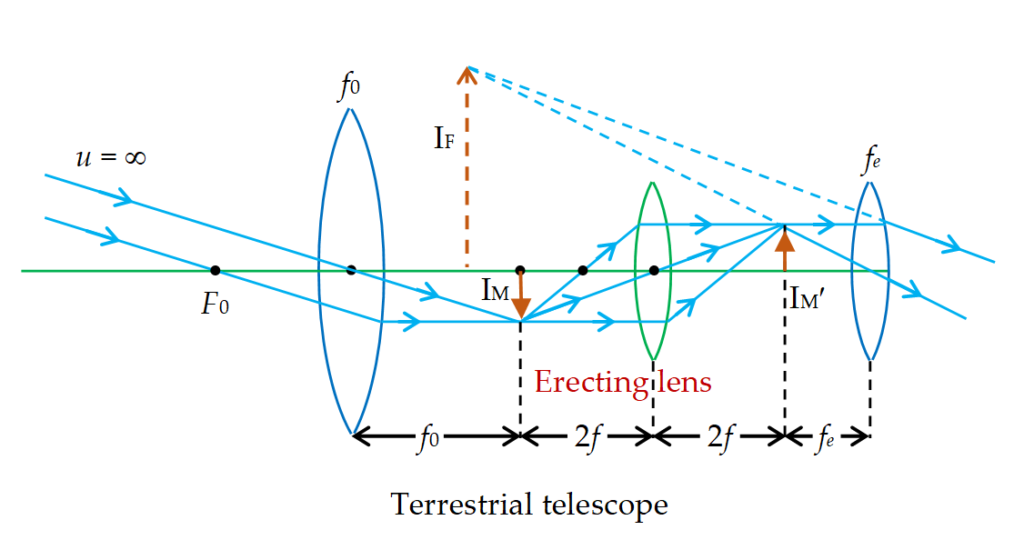
In the astronomical telescope, a lens of short focal length f is placed at 2f from intermediate image (figure), it will erect the intermediate image at a distance 2f on the other side of it and this image will act as an object for eye lens. So now the final image will be erect with respect to object. This lens is called erecting lens and as for it m = –1, the MP and length of telescope for relaxed eye will be
MP = \displaystyle -\frac{{{{f}_{0}}}}{{{{f}_{e}}}}\times (-1)=\frac{{{{f}_{0}}}}{{{{f}_{e}}}}
\displaystyle L={{f}_{0}}+{{f}_{e}}+4f
This telescope is called terrestrial telescope and is used to see distant terrestrial objects such as a cliff or a tree.
Reflecting type telescope (Newtonian)
The objective is large concave parabolic spherical mirror made of speculum metal (alloy of copper and tin). A Ramsdens eyepiece is used with this model.
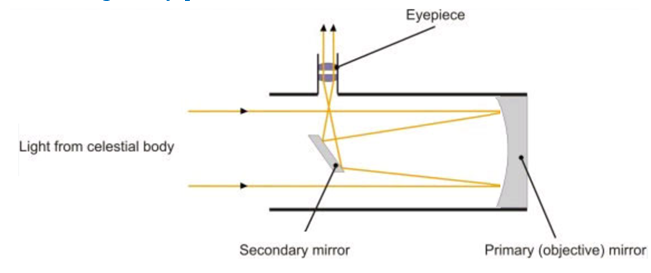
The rays from the distant stars/planets after reflection from the objective mirror (concave mirror of large aperture and large focal length) are reflected to one side at right angles to the axis of the objective mirror, with the help of a small plane mirror, as shown in the sketch. Thereafter viewer sees the final image through the eyepiece.
Resolving power and Limit of Resolution
Resolving power of eye
If we assume that the pupil of the eye is about 2 mm in diameter, then eye can see two point sources distinctly if they subtend an angle of one minute of arc i.e. \displaystyle 1/{{60}^{{th}}} of a degree.
This angle is called limit of resolution. The reciprocal of this angle is called the resolving power of eye.
The resolving power of human eye = \frac{a}{\lambda } where, \displaystyle \lambda = wavelength of light used and a = diameter of pupil
Limit of resolution (LOR) of a microscope
The limit of resolution of a microscope is the least distance between the two point objects which can be distinguished. This distance d is given by
d=\frac{\lambda }{{2\mu \sin \theta }}
where \displaystyle \lambda = wavelength of light used,
\displaystyle \mu = refractive index of the medium between objects and lens of microscope
\displaystyle \theta = half angle of the cone of light from the angle between the outermost ray entering the objective and the optical axis.
Resolving power is (1/d).
therefore RP of a microscope
=\frac{1}{{\text{LOR}}}=\frac{{2\mu \sin \theta }}{\lambda }.
Where, ( \displaystyle \mu \sin \theta ) is called numerical aperture. It is 0.004 for human eye.
Resolving power of Telescope
RP of a terrestrial telescope is same as that of an astronomical telescope. However, because terrestrial telescope has an additional auxiliary lens for erecting the orientation of the final image, the amount of light absorbed by it reduces its resolving power to some extent.
RP of telescope =\frac{d}{{1.22\lambda }}
Further, RP = 1/LOR
hence LOR of telescope =\frac{{1.22\lambda }}{d}
Defects Of Lenses
(i)Chromatic aberration in a lens:
The inability of a lens to form a white and distinct image of a white object is called chromatic aberration.Actually the deviation angle produced by a lens depends on refractive index of the material of the lens. Where as the refractive index depends on the wavelength of the light ray. Due to this when a white light pases through a lens its different colors are deviated by different angles and produce a spectrum along the principal axis. Hence if a screen is kept to obtain the image it will have coloured edges around it. This is explained below.
The chromatic aberration arises due to variation of focal length f of a lens with refractive index \displaystyle \mu as given below:
\displaystyle \frac{1}{f}=(\mu -1)\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
Now, as \displaystyle \mu changes with wavelength \displaystyle \lambda in accordance with Cauchy’s equation,
\displaystyle \mu =A+\frac{B}{{{{\lambda }^{2}}}}
and \displaystyle {{\lambda }_{R}}>{{\lambda }_{V}}
Hence \displaystyle {{\mu }_{V}}>{{\mu }_{R}}
and \displaystyle {{f}_{V}}<{{f}_{R}}
Hence, for a white object, images of different colors are formed at different places and are of different sizes. These defects are called longitudinal chromatic aberration and lateral chromatic aberration respectively.
Longitudinal chromatic aberration
It is given by the axial distance between the red and violet images and is equal to ( \displaystyle {{v}_{R}}-{{v}_{V}}). It is given by
\displaystyle {{v}_{R}}-{{v}_{V}}=\frac{{\omega {{v}^{2}}}}{f}
where \displaystyle \omega = dispersive power, \displaystyle {{v}_{R}} = distance of the red image, \displaystyle {{v}_{v}} = distance of the violet image and v = mean distance of the yellow image.
If the object is an infinity, \displaystyle {{v}_{R}}={{f}_{R}}, \displaystyle {{v}_{V}}={{f}_{V}} and v = f.
So, \displaystyle {{f}_{R}}-{{f}_{V}}=\frac{{\omega {{f}^{2}}}}{f}=\omega f
Because for a lens, neither \omega nor f is zero, hence \displaystyle {{f}_{R}}-{{f}_{V}}can never be equal to zero, i.e. a single lens cannot give an image free from chromatic aberration.
Lateral chromatic aberration
The formation of images of different colors in different sizes gives rise to lateral chromatic aberration. This is given by the difference in the sizes of the images of red and violet colors.
We know that \displaystyle \frac{I}{O}=\frac{v}{u}. Applying this for Red and Voilet colour to get \displaystyle {{I}_{R}} and {{I}_{V}} i.e. size of image produced by Red and voilet wavelengths.
We get \displaystyle {{I}_{R}}=\frac{{{{v}_{R}}}}{{{{u}_{R}}}}O and \displaystyle {{I}_{V}}=\frac{{{{v}_{V}}}}{{{{u}_{V}}}}O.
On subtracting them we get Lateral chromatic aberration i.e.
\displaystyle {{I}_{R}}-{{I}_{V}}=\frac{{{{v}_{R}}O}}{u}-\frac{{{{u}_{V}}O}}{u}=({{u}_{R}}-{{u}_{V}})\frac{O}{u}=\left( {\frac{{\omega {{v}^{2}}}}{f}} \right)\left( {\frac{O}{u}} \right)
Achromatism
The phenomenon of removing the longitudinal and lateral chromatic aberrations in the image formed by a lens is called as achromatism. The combination of lenses free from chromatic aberrations is called an achromatic combination.
Two thin lenses of focal length \displaystyle {{f}_{1}} and \displaystyle {{f}_{2}} and of materials of dispersive powers \displaystyle {{\omega }_{1}} and \displaystyle {{\omega }_{2}} placed in contact form an achromatic combination if
\displaystyle \frac{{{{\omega }_{1}}}}{{{{f}_{1}}}}+\frac{{{{\omega }_{2}}}}{{{{f}_{2}}}}=0
or \displaystyle {{\omega }_{1}}{{P}_{1}}+{{\omega }_{2}}{{P}_{2}}=0
In order to obtain achromatic combination of two lenses, following four requirements are essential.
(a) One lens must be convex, the other must be concave.
(b) The two lenses must be made of different materials.
(c) The power of convex lens must be greater than that of concave lens of flint glass.
(d) Convex lens must be made of crown glass while concave lens of flint glass.
NOTE:
Two thin lenses of same material and focal lengths \displaystyle {{f}_{1}} and \displaystyle {{f}_{2}} also form an achromatic combination when the separation d between them is:
\displaystyle d=({{f}_{1}}+{{f}_{2}})/2
Illustration
A simple microscope consists of a convex lens of power +25D and a concave lens of power –20D in contact. Find the magnifying power when final image is formed (a) at infinity (b) at a distance of distinct vision.
Solution
Here {{P}_{1}}=+25\mathbf{D},\ \,\,{{P}_{2}}=-20\mathbf{D}, D = 25 cm
Since lenses are in contact, so power of the combination
P={{P}_{1}}+{{P}_{2}}=25-20=+5\mathbf{D}
therefore Focal length of the combination, f=\frac{{100}}{P}=\frac{{100}}{5}=20\text{cm}
(a)
Magnifying power when final image is formed at \displaystyle \infty ,
M.P.=\frac{D}{f}=\frac{{25}}{{20}}=1.25
(b)
Magnifying power when final image is formed at the distinct vision,
M.P.=1+\frac{D}{f}=1+\frac{{25}}{{20}} =1+1.25=2.25.
Illustration
The focal lengths of the objective and eye-piece of a microscope are 2 cm and 5 cm respectively and the distance between them is 25 cm. Find the distance of the object from the objective, when the final image is formed at the distance of distinct vision. Also find the magnifying power of the microscope.
Solution
Here, \displaystyle {{f}_{o}} = 2 cm, \displaystyle {{f}_{e}} = 5 cm
\displaystyle {{v}_{o}} = – 25 cm (Distance of image from eyepiece)
Using \displaystyle -\frac{1}{{{{u}_{e}}}}+\frac{1}{{{{v}_{e}}}}=\frac{1}{{{{f}_{e}}}}
or \displaystyle -\frac{1}{{{{u}_{e}}}}=\frac{1}{{{{f}_{e}}}}-\frac{1}{{{{v}_{e}}}}=\frac{1}{5}+\frac{1}{{25}}=\frac{6}{{25}}
or \displaystyle {{u}_{e}}=-\frac{{25}}{6}\ \text{cm}.
This is the distance of the real image formed by the objective from the eyepiece.
Given that \displaystyle |{{v}_{o}}|+|{{u}_{e}}| = 25 cm
or \displaystyle |{{v}_{o}}|\ =25-|u|\,=25-\frac{{25}}{6}=\frac{{125}}{6}\ \text{cm}
which is the distance of the image from the objective.
Using \displaystyle -\frac{1}{{{{u}_{o}}}}+\frac{1}{{{{v}_{o}}}}=\frac{1}{{{{f}_{o}}}}
or \displaystyle -\frac{1}{{{{u}_{o}}}}=\frac{1}{{{{f}_{o}}}}-\frac{1}{{{{v}_{o}}}}=\frac{1}{2}-\frac{6}{{125}}=\frac{{125-12}}{{250}}
\displaystyle =\frac{{113}}{{250}}
or \displaystyle {{u}_{o}}=-\frac{{250}}{{113}}\ \text{cm}
which is the distance of the object from the objective.
\displaystyle M.P.=\left| {\frac{{{{v}_{o}}}}{{{{u}_{o}}}}} \right|\ \left( {1+\frac{D}{{{{f}_{e}}}}} \right)
\displaystyle =\frac{{125/6}}{{250/113}}\left( {1+\frac{{25}}{5}} \right)=\frac{{125}}{6}\times \frac{{113}}{{250}}\times 6 \displaystyle =\frac{{113}}{2}=56.5
Illustration
The moon is seen through a telescope having objective lens of focal length 80 cm and eye-piece of focal length 4 cm. The diameter of the moon is \displaystyle 3\times {{10}^{5}}km and its distance from the earth is \displaystyle 3.75\times {{10}^{8}} km. Calculate (i) magnifying power of the telescope (ii) length of the telescope (iii) angular size of the image of the moon.
Solution
Here \displaystyle {{f}_{o}} = 80 cm, \displaystyle {{f}_{e}} = 4 cm
Diameter of the moon = \displaystyle 3\times {{10}^{5}}km
Distance of moon from the telescope = \displaystyle 3.75\times {{10}^{8}} km
Distance of moon from the telescope = \displaystyle 3.75\times {{10}^{8}} km.
(i)
Magnifying power, M.P. \displaystyle =\frac{{{{f}_{o}}}}{{{{f}_{e}}}}=\frac{{80}}{4}=20
(ii)
Length of telescope = \displaystyle {{f}_{o}}+{{f}_{e}}= 80 + 4 = 84 cm
(iii)
Also M.P. \displaystyle =\frac{\beta }{\alpha }
Here \displaystyle \alpha =\frac{{3\times {{{10}}^{5}}}}{{3.75\times {{{10}}^{8}}}}
\displaystyle =\frac{{300}}{{375}}\times {{10}^{{-3}}}=\frac{4}{5}\times {{10}^{{-3}}}\ \text{rad}
\displaystyle =\frac{4}{5}\times {{10}^{{-3}}}\times \frac{{180}}{\pi }=0.05{}^\circ
or \displaystyle \beta =\text{M}\text{.P}\text{.}\times \alpha =20\times 0.05{}^\circ = 1°
Illustration
The focal lengths of the objective and eye piece of an astronomical telescope are 25 cm and 2.5 m respectively. The telescope is focused on an object 1.5 m from objective, the final image being formed 25 cm from eye of the observer. Calculate the length of telescope.
Solution
Using lens formula, we get
\displaystyle \frac{1}{v}-\frac{1}{{150}}=-\frac{1}{{25}}
or , \displaystyle \frac{1}{v}=\frac{1}{{150}}-\frac{1}{{25}}
i.e., \displaystyle v=-30\ \text{cm}
This image serves as an object for the eyepiece. Using lens formula again we get
\displaystyle \frac{1}{{25}}-\frac{1}{u}=-\frac{1}{{2.5}}
i.e., \displaystyle -\frac{1}{u}=-\frac{1}{{2.5}}-\frac{1}{{25}}
i.e., u = 2.27 cm
Length of telescope = 30 + 2.27 = 32.27 cm
Practice Questions (Basic Level)
Q.1
A microscope has an objective of focal length 1.5 cm and an eye –piece of focal length 2.5 cm. If the distance between objective and eye-piece is 25 cm, what is the approximate value of magnification produced for relaxed eye?
(a) 75 (b) 110 (c) 140 (d) 25
Ans. (c)
Practice Questions (JEE Main Level)
Q.1
A compound microscope consists of an objective of focal length fo and an eyepiece with magnification 25. The microscope is designed so that the object is focused in a plane 16 cm away from the focal point of the objective lens. When properly adjusted, the eyepiece and the objective are 17.4 cm apart. What is fo? (Assume that the eyepiece magnification is based on an image at infinity and a near point at 25 cm).
(a) 0.4 cm (b) 0.2 cm (c) 0.3 cm (d) 0.4 cm
Ans. (a)
Q.2
The objective and the eyepiece of a refracting telescope have focal lengths of 320 cm and 4 cm respectively. The telescope is used to view Neptune and the final image is set at infinity. The diameter of Neptune is 4.96 × 107 m and the distance from Earth at the time of observation is 4.4 × 1012 m. Find the angle subtended by the final telescopic image of Neptune.
(a) 0.8 m rad (b) 0.9 m rad (c) 0.7 m rad (d) 0.6 m rad
Ans. (b)
Q.3
An astronomial telescope has an angular magnification of magnitude 5 for distant objects. The separation between the objective and eyepiece is 36 cm and the final image is formed at infinity. Determine the focal length of objective and eyepiece.
(a) fo = 20 and fe = 5 cm
(b) fo = 10 and fe = 8 cm
(c) fo = 30 and fe = 6 cm
(d) fo = 10 and fe = 5 cm
Ans. (c)
Q.4
The magnifying power of a telescope is found to be 9 and the separation between the lenses is 20 cm for relaxed eye. What are the focal lengths of the component lenses?
(a) fo = 16 cm and fe = 1 cm
(b) fo = 17 cm and fe = 3 cm
(c) fo = 16 cm and fe = 4 cm
(d) fo = 18 cm and fe = 2 cm
Ans. (d)
Q.5
The total magnification produced by a compound microscope is 20. The magnification produced by the eyepiece is 5. The microscope is focused on a certain object. The distance between the objective and eyepiece is observed to be 14 cm. If least distance of distinct vision is 20 cm. Calculate focal length of the objective and the eyepiece.
(a) \displaystyle {{f}_{e}}=4cm\,\,and\,\,\,{{f}_{o}}=\,3\,cm
(b) \displaystyle {{f}_{e}}=5cm\,\,and\,\,\,{{f}_{o}}=\,2\,cm
(c) \displaystyle {{f}_{e}}=6cm\,\,and\,\,\,{{f}_{o}}=\,1\,cm
(d) \displaystyle {{f}_{e}}=8cm\,\,and\,\,\,{{f}_{o}}=\,4\,cm
Ans. (b)
Q.6
A convex lens of focal length 25 cm is placed coaxially in contact with a concave lens of focal length 20 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
(a) –1 D ; Divergent
(b) 1 D ; Convergent
(c) –0.5 D ; Divergent
(d) 0.5 D ; Convergent
Ans. (a)
Q.7
A compound microscope uses an objective lens of focal length 4 cm and eyepiece lens of focal length 10 cm. An object is placed at 6 cm from the objective lens. Calculate the magnifying power of the compound microscope. Also, calculate the length of the microscope.
(a) \displaystyle M=-6,\,\,Length\,\,=\,\,18.14\,cm
(b) \displaystyle M=-7,\,\,Length\,\,=\,\,17.14\,cm
(c) \displaystyle M=-5,\,\,Length\,\,=\,\,16.14\,cm
(d) \displaystyle M=-7,\,\,Length\,\,=\,\,19.14\,cm
Ans. (d)
Q.8
Two convex lenses of focal length 20 cm and 1 cm constitute a telescope. The telescope is focused on a point which is 1m away from the objective. Calculate the magnification produced and the length of the tube if the final image is formed at a distance 25 cm from the eyepiece.
(a) \displaystyle M\,=-5.5 and \displaystyle L\,=26.96\,\,cm
(b) \displaystyle M\,=-8.5 and \displaystyle L\,=22.96\,\,cm
(c) \displaystyle M\,=-6.5 and \displaystyle L\,=25.96\,\,cm
(d) \displaystyle M\,=-4.5and \displaystyle L\,=23.96\,\,cm
Ans. (c)
Q.9
The objective of an astronomical telescope has a diameter of 150 mm and a focal length of 4.00 m. The eyepiece has a focal length of 25.00 mm. Calculate the resolving power of telescope.
(X = 6000A for yellow colour)
(a) \displaystyle 0.34\,\times \,{{10}^{7}}
(b) \displaystyle 0.34\,\times \,{{10}^{6}}
(c) \displaystyle 0.34\,\times \,{{10}^{4}}
(d) \displaystyle 0.24\,\times \,{{10}^{6}}
Ans. (b)
Q.10
An astronomical telescope uses two lenses of powers 10 D and 1 D. What is its magnifying power in normal adjustment?
(a) –10 (b) 10 (c) –9 (d)–11
Ans. (a)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
