Video Lecture
Theory For Making Notes
Moment of Inertia
One of the most fundamental characteristics possessed by an object is its intrinsic reluctance to accept a change in its state of motion i.e. its inertia
A body needs a force to start its translational inertial is better known as mass.
The measure of a body’s rotational inertia is called moment of inertia and it is represented by I. The moment of inertia of a body is a function of the mass of the body, the distribution of that mass and around the axis of rotation.
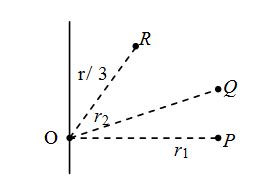
Consider a particle of mass m situated at a distance r from the axis as shown in figure. Its moment of inertia I is defined as
I = mr2 … (v)
If a system of particles is made of number of particles of masses m1, m2, m3 …. mn at distance r1, r2, r3, …. rn from the axis of rotation, its moment of inertia is defined as
\displaystyle I={{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}+{{m}_{3}}r_{3}^{2}+….+{{m}_{n}}r_{n}^{2}
\displaystyle =\sum\limits_{{i\,\,=\,\,1}}^{{i\,\,=\,\,n}}{{{{m}_{i}}r_{i}^{2}}} … (vi)
Important Point About Moment Of Inertia
(1)
Moment of inertia of a particle I=m{{r}^{2}}; where r is the perpendicular distance of particle from rotational axis.
(2)
Moment of inertia of a body made up of number of particles (discrete distribution)
I={{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}+{{m}_{3}}r_{3}^{2}+…….
(3)
Moment of inertia of a continuous distribution of mass, treating the element of mass dm at position r as particle
dI=dm\,{{r}^{2}} i.e., I=\int{{{{r}^{2}}dm}}
(4)
Dimension : [M{{L}^{2}}{{T}^{0}}]
(5)
S.I. unit : kgm2.
(6)
Moment of inertia depends on mass, distribution of mass and on the position of axis of rotation.
(7)
Moment of inertia does not depend on angular velocity, angular acceleration, torque, angular momentum and rotational kinetic energy.
(8)
It is not a vector as direction (clockwise or anti-clockwise) is not to be specified and also not a scalar as it has different values in different directions. Actually it is a tensor quantity.
(9)
In case of a hollow and solid body of same mass, radius and shape for a given axis, moment of inertia of hollow body is greater than that for the solid body because it depends upon the mass distribution.
Moment of inertia of continuous body
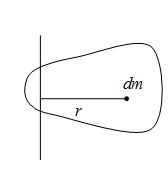
For calculating moment of inertia of a continuous body, we first divide the body into suitably chosen infinitesimal elements. The choice depends on symmetry of body. Consider an element of the body at a distance r from the axis of rotation. The moment of inertia of this element about the axis we defined as (dm)r2 and the discrete sum over particles becomes integral over the body:
\displaystyle I=\int{{(dm){{r}^{2}}}} … (vii)
Moment of Inertia for different bodies
1. Moment of inertia of a rod
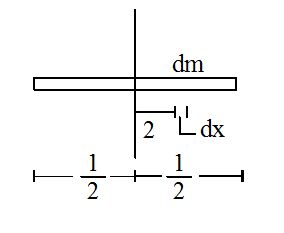
(a) About an axis passing through its centre and perpendicular to its length. Considering a small element of the rod of length dx and mass dm at a distance x from the axis where
\displaystyle dm=\frac{M}{L}.dx.
The moment of inertia of this element about the given axis is dI = dm . x2 = \displaystyle \frac{M}{L}\ .\ dx\ .\ {{x}^{2}}
Hence the moment of inertia of whole rod is
I = \displaystyle \int\limits_{{-L/2}}^{{L/2}}{{\frac{M}{L}\ {{x}^{2}}\,.\,dx=\frac{{M{{L}^{2}}}}{{12}}}}
(b) About an axis touching the edge of the rod and perpendicular to the length of the rod.
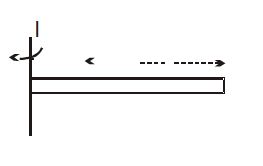
It can be obtained by using the limits from zero to L
where \displaystyle \int\limits_{0}^{L}{{\frac{M}{L}\ {{x}^{2}}\,.\,dx=\frac{{M{{L}^{2}}}}{3}}}
I = \displaystyle \frac{{M{{L}^{2}}}}{3}
2.Uniform Circular ring:
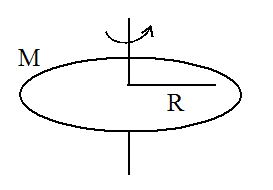
If M is the mass of the ring with radius R, then moment of inertia about an axis passing through the center of ring perpendicular to its plane can be obtained by
\displaystyle I=\int_{O}^{M}{{dm{{R}^{2}}}}={{R}^{2}}\int\limits_{O}^{M}{{dm}}=M{{R}^{2}}
3.Uniform circular Disc:
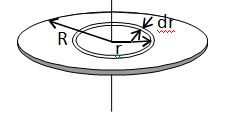
Uniform circular disc about an axis passing through its centre and perpendicular to its plane. Dividing the disc into a number of concentric rings and considering one ring of radius r and thickness dr. Let due to the mass of the disc and
(i) given by \displaystyle dm=\frac{M}{{\pi {{R}^{2}}}}2\pi rdr
The moment of inertia about the given axis of this ring
(ii) \displaystyle dI=dm.{{r}^{2}}=\left[ {\frac{M}{{{{R}^{2}}}}2rdr} \right].{{r}^{2}}therefore the moment of inertia of the whole disc is given by
\displaystyle I=\int\limits_{0}^{R}{{\frac{{2M}}{{{{R}^{2}}}}.{{r}^{2}}dr=\frac{{M{{R}^{2}}}}{2}}}
It may be noted that the moment of inertia of a disc and of a ring is independent of their thickness.
Moment of Inertia of Some Common Shaped Bodies
A Thin Rod The axis is perpendicular to the rod and passing through its centre. Ic = \displaystyle \frac{{M{{L}^{2}}}}{{12}} | 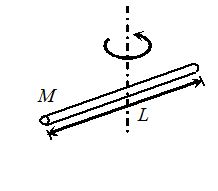 | A Thick Rod The axis is perpendicular to the rod and passing through the centre. {{I}_{c}}=\frac{{M{{L}^{2}}}}{{12}}+\frac{{M{{R}^{2}}}}{4} | 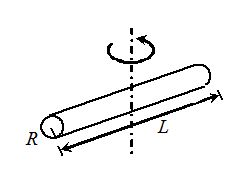 |
A Ring
Axis is perpendicular to the plane of the ring \displaystyle {{I}_{c}}=M{{R}^{2}} | 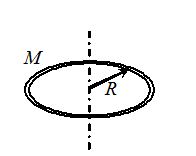 | A Hollow Cylinder \displaystyle {{I}_{c}}=M{{R}^{2}} | 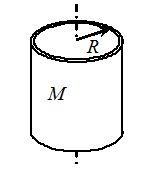 |
A Disc The axis perpendicular to the plane of the disc. {{I}_{c}}=\frac{{M{{R}^{2}}}}{2} | 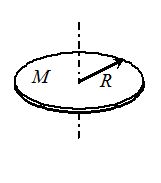 | A Solid Cylinder {{I}_{c}}=\frac{{M{{R}^{2}}}}{2} | 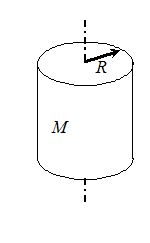 |
A thin rod about a perpendicular axis through its end. I = \frac{{M{{L}^{2}}}}{3} | 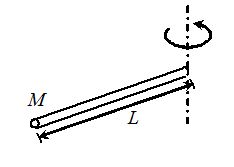 | A rectangular plate about one edge. I = \frac{{M{{L}^{2}}}}{3} | 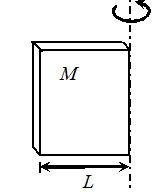 |
A Solid Sphere About its diameter katex] {{I}_{c}}=\frac{2}{5}M{{R}^{2}}[/katex] | 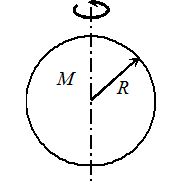 | A Hollow Sphere About its diameter {{I}_{c}}=\frac{2}{3}M{{R}^{2}} | 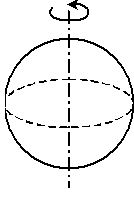 |
Annular Disc About an axis perpendicular to plane of disc \displaystyle {{I}_{c}}=\frac{m}{2}(R_{1}^{2}+R_{2}^{2}) | 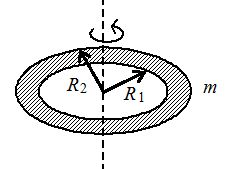 | Thick Hollow cylinder About axis of the cylinder \displaystyle I=\frac{m}{2}(R_{1}^{2}+R_{2}^{2}) | 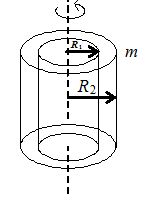 |
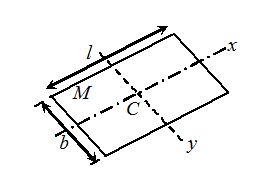
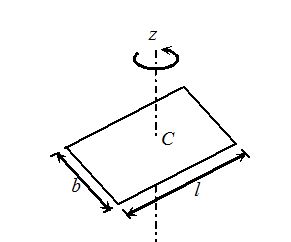
A Rectangular Plate Axes lying in the plane of the plate and passing through c.m. , \displaystyle {{I}_{x}}=\frac{{M{{b}^{2}}}}{{12}}, {{I}_{y}}=\frac{{M{{\ell }^{2}}}}{{12}} | Axis perpendicular to plane and passing through its c.m. \displaystyle {{I}_{z}}=\frac{{M({{l}^{2}}+{{b}^{2}})}}{{12}}
| ||
Theorems on moment of inertia
Theorem of perpendicular axis
This theorem is applied only to a plane lamina. It is stated as follows:
The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in its own plane intersecting each other at the point through which the perpendicular axis passes.
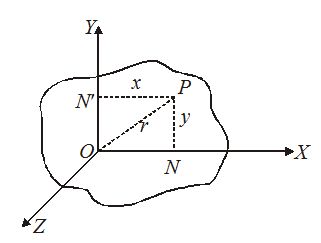
Proof:- Let us consider a plane lamina lying in the XOY plane. The lamina can be supposed to be made up of a large number of particles. Consider a particle of mass m at P. From P, drop perpendiculars PN and PN’ on X-axis and Y-axis respectively.
Now, PN’ = x and PN = y
Moment of inertia of particle about X-axis = my2
Moment of inertia of the whole of lamina about X-axis,
{{I}_{x}}=\sum{{m{{y}^{2}}}}
Moment of inertia of the whole of lamina about Y-axis,
{{I}_{y}}=\sum{{m{{x}^{2}}}}
Moment of inertia of the whole of lamina about Z-axis,
{{I}_{z}}=\sum{{m{{r}^{2}}}}
But {{r}^{2}}={{x}^{2}}+{{y}^{2}}
∴ {{I}_{z}}=\sum{{m({{x}^{2}}+{{y}^{2}}}})=\sum{{m{{x}^{2}}}}+\sum{{m{{y}^{2}}}}
or {{I}_{z}}={{I}_{y}}+{{I}_{x}}
Theorem of parallel axes
This theorem is applicable not only to a plane lamina but also to a three-dimensional body. It is stated as follows:
The moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of gravity plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.
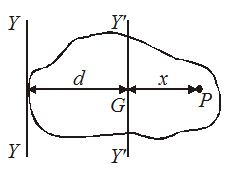
Proof:- Let I be the moment of inertia of a plane lamina about an axis YY. Let G be the centre of gravity of the lamina. Y’Y’ is an axis parallel to the given axis and passing through the centre of gravity G of the lamina. Let Ig be the moment of inertia of the lamina about Y’Y’.
Consider a particle of mass m at P. Let d be the perpendicular distance between parallel axes YY and Y’Y’. Let GP = x.
Moment of inertia of the particle about YY = m (x + d)2
Moment of inertia of the whole of lamina about YY,
I=\sum{{m{{{(x+d)}}^{2}}}}=\sum{{m({{x}^{2}}+{{d}^{2}}+2xd)}}
or I=\sum{{m{{x}^{2}}}}+\sum{{m{{d}^{2}}+}}\sum{{2mxd}}
But \sum{{m{{x}^{2}}}}={{I}_{g}}, \sum{{m{{d}^{2}}}}=\left( {\sum{m}} \right){{d}^{2}}=M{{d}^{2}}
Where m\left( {=\sum{m}} \right) is the mass of the lamina.
Also, \sum{{2mxd}}=2d\sum{{mx}}
I={{I}_{g}}+M{{d}^{2}}+2d\sum{{mx}} …(1)
The lamina will balance itself about its centre of gravity. So, the algebraic sum of the moments of the ‘weights of constituent particles’ about the centre of gravity G should be zero.
\sum{{mg}}\times x=0or g\sum{{mx}}=0
or \sum{{mx}}=0 [\because \ \ g\ne 0]
From equation (1), \displaystyle I={{I}_{g}}+M{{d}^{2}}
Radius of Gyration
It is defined as the distance from the axis of rotation at which if whole mass of the body were supposed to be concentrated, the moment of inertia would be the same as with the actual distribution of mass. It is denoted by K.
The moment of inertia of a body of mass M and radius of gyration K is given by
I = MK2 …(1)
Also, I={{m}_{1}}r_{1}^{2}+{{m}_{1}}r_{2}^{2}+\ldots +{{m}_{n}}r_{n}^{2}
If {{m}_{1}}={{m}_{2}}=\ldots {{m}_{n}}=m\,(\text{say),}\ \text{then}
I=m\,(r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2})or I=mn\,\left( {\frac{{r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2}}}{n}} \right)
But mn=M(\text{mass}\ \text{of}\ \text{body})
I=M\,\left( {\frac{{r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2}}}{n}} \right) …(2)
Comparing (1) and (2), we get
M{{K}^{2}}=M\,\left( {\frac{{r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2}}}{n}} \right)
or {{K}^{2}}=\,\frac{{r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2}}}{n}or K=\sqrt{{\frac{{r_{1}^{2}+r_{2}^{2}+\ldots +r_{n}^{2}}}{n}}}
The radius of gyration of a body about an axis is equal to the root mean square distance, of the various particles constituting the body, from the axis of rotation.
Rotational Kinetic Energy
Consider a rigid body rotating about a fixed axis with angular velocity w. The body can be supposed to be made up of a large number of particles m1, m2, …, mn at distances r1, r2, …, rn respectively, from the axis of rotation. Each particle has a kinetic energy. The kinetic energy of the body will be the sum of the kinetic energies of all the particles. If υ1, υ2, …, υn be the linear speeds of the particles, respectively, then the kinetic energy of the body can be written as
\displaystyle {{E}_{k}}=\sum \frac{1}{2}{{m}_{i}}{{\upsilon }_{i}}^{2}
But \displaystyle {{\upsilon }_{i}}={{r}_{i}}\omega
\displaystyle {{E}_{k}}=\sum \frac{1}{2}{{m}_{i}}{{r}_{i}}^{2}{{\omega }^{2}}= \displaystyle \frac{1}{2}\left( {\sum {{m}_{i}}{{r}_{i}}^{2}} \right){{\omega }^{2}}
\displaystyle {{E}_{k}}=\frac{1}{2}I{{\omega }^{2}}
Where I is the moment of inertia of the body. From this expression it is clear that moment of inertia is the rotational analogue of mass.
Illustration
A thin uniform wire of length l and mass m is bent in the form of a semi-circle. Calculate its moment of inertia about an axis (Y’OY) passing through the free ends.
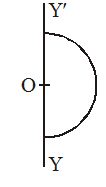
Solution
\displaystyle \pi r=l or r=\frac{l}{\pi }
I=\frac{1}{2}m{{r}^{2}}
I=\frac{1}{2}m\frac{{{{l}^{2}}}}{{{{\pi }^{2}}}}=\frac{{m{{l}^{2}}}}{{2{{\pi }^{2}}}}Ans.
Illustration
The moment of inertia of a uniform circular disc about a diameter is I. What is the moment of inertia about an axis perpendicular to its plane and passing through a point on its rim?
Solution:
Applying theorem of parallel axes, M.I. about the given axis
=\frac{1}{2}M{{R}^{2}}+M{{R}^{2}}=\frac{3}{2}M{{R}^{2}} =6\times \frac{1}{4}M{{R}^{2}}=6I Ans.
Illustration
The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is I1, I2, I3 and I4 are respectively the moment of inertia about axes 1, 2, 3 and 4 which are in the plane of the plate. Then which is incorrect?
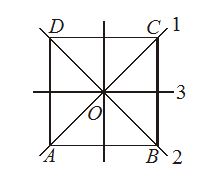
(1) {{I}_{1}}+{{I}_{2}}=I (2) {{I}_{3}}+{{I}_{4}}=I
(3) {{I}_{4}}+{{I}_{3}}=I (4) {{I}_{1}}+{{I}_{2}}+{{I}_{3}}+{{I}_{4}}=I
Solution:
According to perpendicular axis theorem, the sum of the rotational inertias of a plane laminar body (i.e., thin plate) about any two perpendicular axes in the plane of the body is equal to the rotational inertia of the body about an axis through their point of intersection perpendicular to the plane.
I={{I}_{1}}+{{I}_{2}}
={{I}_{3}}+{{I}_{4}}
{{I}_{1}}={{I}_{2}};\ {{I}_{3}}={{I}_{4}} (symmetry of body)
I=2\ {{I}_{2}}=2\ {{I}_{3}}
∴ {{I}_{2}}={{I}_{3}}
I={{I}_{1}}+{{I}_{3}}
∴ Option (4) Is The Correct Answer.
Practice Questions (Level-1)
1.
Moment of inertia is a
(a) scalar quantity
(b) vector quantity
(c) neither scalar nor vector
(d) sometimes scalar and sometimes vector
Ans (c)
2.
The ratio of radii of gyration of a circular disc and a circular ring of the same mass and radii about a tangential axis in their plane is
(a) 1:\sqrt{2}
(b) \sqrt{5}:\sqrt{6}
(c) \sqrt{2}:\sqrt{3}
(d) \sqrt{2}:1
Ans(b)
3.
A thin square plate of side a is rotating with one of its diagonal as its axis of rotation. If its angular velocity is w and mass is M. What is its total kinetic energy?
(a) \frac{{M{{a}^{2}}{{\omega }^{2}}}}{{12}}
(b) \frac{{M{{a}^{2}}{{\omega }^{2}}}}{{24}}
(c) \frac{{M{{a}^{2}}{{\omega }^{2}}}}{6}
(d) \frac{{M{{a}^{2}}{{\omega }^{2}}}}{4}
Ans (b)
4.
Two solid sphere of mass m and radius R are stuck to the ends of a thin rod of mass m and length 3R. Find the moment of inertia of the system about the axis at the mid point of the rod and perpendicular to it, as shown in figure.
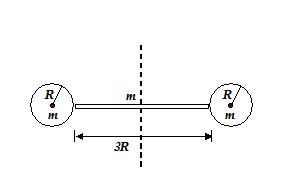
(a)15.2 MR2
(b) 15.5 MR2
(c)14.1 MR2
(d)14.7 MR2
Ans (c)
5.
Three masses m1, m2 and m3 are located at the vertices of an equilateral triangle of side length a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
(a) \frac{{{{a}^{-2}}}}{4}\left[ {{{m}_{2}}+{{m}_{3}}} \right]
(b) \frac{{{{a}^{2}}}}{4}\left[ {{{m}_{2}}+{{m}_{3}}} \right]
(c) \frac{{{{a}^{2}}}}{4}\left[ {{{m}_{2}}+{{m}_{5}}} \right]
(d) \frac{{{{a}^{2}}}}{4}\left[ {{{m}_{3}}+{{m}_{3}}} \right]
Ans (b)
6.
Calculate the moment of inertia of a circular disc of radius 10 cm, thickness 5 mm and density 8 g/cc about a transverse axis passing through the center of the disc.
(a)6.28 x10-4 g cm2
(b)6.30 x 10-4 g cm2
(c)6.30 x 104 g cm2
(d)6.28 x 104 g cm2
Ans (d)
7.
Four particles with equal masses M are connected by rod whose mass can be neglected. Find the moment of inertia, about the indicated axis, of the following:
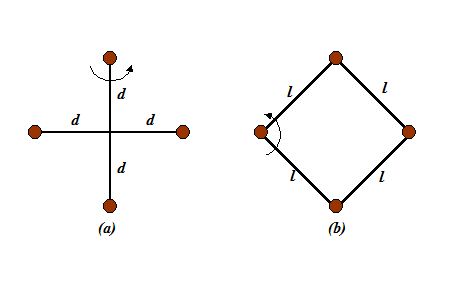
(a)
the cross in figure (a)
(a)8 Md2
(b)7 Md2
(c)3 Md2
(d) 0
Ans (a)
(b)
the square in figure (b)
(a)0
(b)2 Ml2
(c) 4 Ml2
(d)3 Ml2
Ans (c)
8.
A uniform rod of mass M and length L is pivoted about an axis perpendicular to the rod at a distance L/4 from one end. Find the moment of inertia about the point.
(a) \frac{{7M{{L}^{2}}}}{{29}}
(b) \frac{{7M{{L}^{-2}}}}{{48}}
(c) \frac{{-7M{{L}^{2}}}}{{48}}
(d) \frac{{7M{{L}^{2}}}}{{48}}
Ans (d)
Practice Questions (Level-2)
1.
A thin uniform disc of ellipse shape and mass M with major axis 2a and minor axis 2b as shown. We have two axes A and B parallel to minor axis which are distance d and D apart from geometrical centre (D>d). If moment of inertia about axis A is IA. Find moment of inertia about axis B
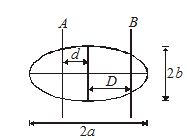
(a) {{I}_{A}}+M{{(D+d)}^{2}}
(b) {{I}_{A}}+M({{D}^{2}}+{{d}^{2}})
(c) {{I}_{A}}+M{{(D-d)}^{2}}
(d) {{I}_{A}}+M({{D}^{2}}-{{d}^{2}})
Ans (a)
2.
For the uniform ‘T’ shaped structure, with mass 3M, moment of inertia about an axis normal to the plane and passing through ‘O’ would be:
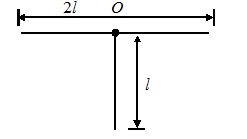
(a) \displaystyle \frac{2}{3}M{{l}^{2}}
(b) M{{l}^{2}}
(c) \frac{{M{{l}^{2}}}}{3}
(d) none of these
Ans (b)
3.
A square lamina is as shown in figure. The moment of inertia of the frame about the three axes shown in figure are I1, I2 and I3 respectively. Select the correct alternative.
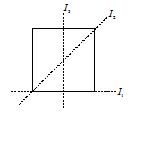
(a) I2 = I3 = I1
(b) I1>I2>I3
(c) I2 = I3<I1
(d) I1<I2<I3
Ans (c)
4.
Two discs have same mass and thickness. Their materials are of densities d1 and d2. The ratio of moment of inertia about an axis passing through the centre and perpendicular to the plane is:
(a) d1 : d2
(b) d2 : d1
(c) 1 : d1 d2
(d) d1 d2 : 1
Ans (b)
5.
A rod is placed along the line y = 2x with its centre at origin. The moment of inertia of the rod is maximum about:
(a) x-axis
(b) y-axis
(c) z-axis
(d) data insufficient
Ans (c)
6.
Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is
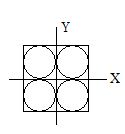
(a) \displaystyle \frac{\pi }{{12}}M{{R}^{2}}
(b) \displaystyle (\frac{4}{3}-\frac{\pi }{4})M{{R}^{2}}
(c) \displaystyle (\frac{4}{3}-\frac{\pi }{6})M{{R}^{2}}
(d) \displaystyle (\frac{8}{3}-\frac{{10\pi }}{4})M{{R}^{2}}
Ans (d)
7.
Three identical rods, each of mass m and length l are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is
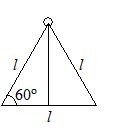
(a) \frac{l}{2}
(b) l \displaystyle \frac{{l\sqrt{3}}}{2}
(c) \frac{l}{{\sqrt{2}}}
(d) \frac{l}{{\sqrt{3}}}
Ans (c)
8.
A can is a hollow cylinder of radius R and height h. Its ends are sealed and it has no seams. The can is made from sheet of areal mass density s kg/m2. What is its moment of inertia about the central axis of symmetry?
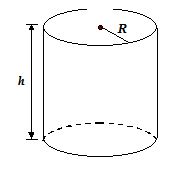
(a) πσR3(3h + R)
(b) πσR3(3h – R)
(c) πσR3(2h + R)
(d) πσR-3(2h – R)
Ans (c)
9.
A uniform sphere of radius a has a concentric spherical cavity of radius b. Find the moment of inertia about a diameter. The mass of the object is M.
(a) \frac{{2M\left( {{{a}^{-5}}-{{b}^{-5}}} \right)}}{{5\left( {{{a}^{3}}-{{b}^{3}}} \right)}}
(b) \frac{{2M\left( {{{a}^{5}}-{{b}^{-2}}} \right)}}{{5\left( {{{a}^{2}}-{{b}^{2}}} \right)}}
(c) \frac{{2M\left( {{{a}^{5}}-{{b}^{5}}} \right)}}{{5\left( {{{a}^{-3}}-{{b}^{-3}}} \right)}}
(d) \frac{{2M\left( {{{a}^{5}}-{{b}^{5}}} \right)}}{{5\left( {{{a}^{3}}-{{b}^{3}}} \right)}}
Ans(d)