Video Lecture
Theory For Making Notes
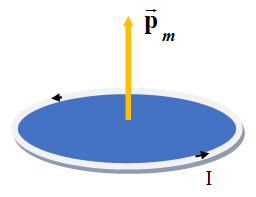
Magnetic Moment
A small current carrying loop acts like a magnetic dipole. The magnitude of a magnetic dipole moment or magnetic moment \displaystyle {{\vec{p}}_{m}} ( In some books it is denoted by m). It is defined as the product of the current in a flat current – carrying loop and the area enclosed by it.
Thus, {{\vec{p}}_{m}}=I.\vec{A}
The direction of magnetic moment coincides with the direction of the area vector (which is the direction of the magnetic field).
If the loop contains N number of turns, the magnetic moment is given by
{{\vec{p}}_{m}}=NI.\vec{A}
Magnetic Moment Of a Charged Particle Moving in a Circle
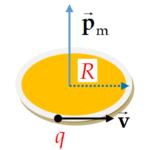
Consider a particle of mass m and having charge q moving with a velocity \displaystyle {\vec{v}} in a circle of radius R. The associated current is
I=\frac{q}{T}=\frac{{q\text{ }v}}{{2\pi R}}
Area of the circular path is
\displaystyle A=\pi {{R}^{2}}
\displaystyle \therefore {{\vec{p}}_{m}}=IA\hat{n}
\displaystyle =\frac{{qv}}{{2\pi R}}\pi {{R}^{2}}\hat{n}
\displaystyle =\frac{1}{2}qvR\hat{n} ——-(1)
But, the angular momentum of this particle is
\displaystyle {\vec{L}}=mvR\hat{n}
\displaystyle \therefore vR\hat{n}=\frac{{\vec{L}}}{m}
therefore from equation (1)
\displaystyle {{\vec{p}}_{m}}=\frac{1}{2}\cdot \frac{{q\vec{L}}}{m}
Thus, the magnetic moment of a charged particle moving in a circle is (q/2m) times its angular momentum. Note that if the charge on the particle is negative (e.g., an electron), then \displaystyle {{\vec{p}}_{m}} is directed opposite to \displaystyle {{\vec{L}}}.
Illustration
A circular loop of wire of radius R carrying a current I is bent about its diameter along two mutually perpendicular planes as shown in the figure given below.
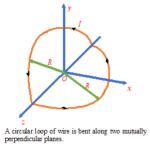
Find the magnetic moment of the loop.
Solution
The magnetic moment of the semicircle in the yz-plane is along the x-axis and that in the xz-plane is along the y-axis.
{{\vec{p}}_{x}}=\left( {\frac{{\pi {{R}^{2}}}}{2}} \right)\ I\ \hat{i} and {{\vec{p}}_{y}}=\left( {\frac{{\pi {{R}^{2}}}}{2}} \right)\ I\ \hat{j}
The magnetic moment of the semicircle lying in the y-z plane is along +x axis and is denoted by \displaystyle {{p}_{x}} and that of the semicircle lying in x-z plane is along +y axis and is denoted by \displaystyle {{p}_{y}} as shown in the diagram given below
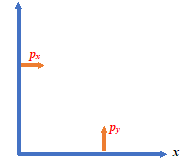
The resultant magnetic moment is given by
\displaystyle \vec{p}={{p}_{x}}\hat{i}+{{p}_{y}}\hat{j}
or \vec{p}=\frac{{\pi {{R}^{2}}I}}{2}\ (\hat{i}+\hat{j})A.m2
Illustration
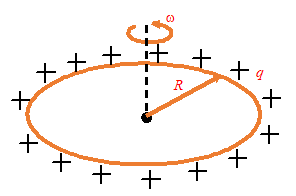
Solution
The motion of charges along with the ring produces current I which is given by
I=\frac{q}{T}=\frac{q}{{2\pi /\omega }}=\frac{{\omega q}}{{2\pi }}
Thus, \displaystyle {{p}_{m}}=IA=\frac{{\omega q}}{{2\pi }}(\pi {{R}^{2}})=\frac{1}{2}\omega q{{R}^{2}}
Illustration
A rotating rod is pivoted about one end and carries a total charge q uniformly distributed along its length L (fig. a). If the rod rotates with angular velocity \displaystyle \omega , compute its magnetic moment.
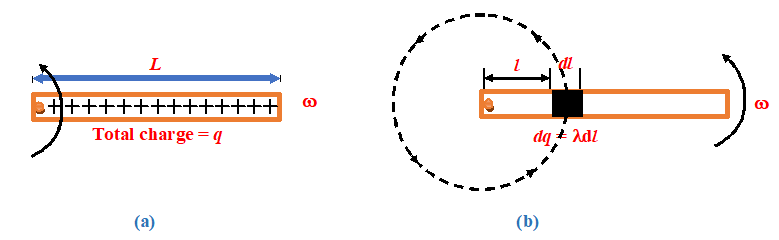
Solution
We visualize the rotating rod of charge as a series of concentric current loop, each carrying a current dI as shown in fig(b). The charge per unit length \displaystyle \lambda along the rod is \lambda =\frac{q}{L}
Now \displaystyle dq=\lambda .dl
and dI=\frac{{dq}}{{(2\pi /\omega )}}=\frac{\omega }{{2\pi }}dq=\frac{\omega }{{2\pi }}\lambda dl
The magnetic moment of this differential current loop is given by
d{{p}_{m}}=dI(\pi {{l}^{2}})=\left( {\frac{\omega }{{2\pi }}\lambda dl} \right)\pi {{l}^{2}}=\frac{{\omega \lambda }}{2}{{l}^{2}}dl
On integrating ,
{{p}_{m}}=\frac{{\omega \lambda }}{2}\ \int\limits_{0}^{L}{{{{l}^{2}}dl=\frac{{\omega \lambda {{L}^{3}}}}{6}}}
Substituting for \displaystyle \lambda , we have
{{p}_{m}}=\frac{{q\omega {{L}^{2}}}}{6}
Torque On a Magnetic Dipole
Just as an electric dipole placed in an electric field experiences a torque, similarly a magnetic dipole (a current loop) placed in a magnetic field experiences a torque.
Consider a rectangular loop of sides a and b, carrying a current I. Let it be placed in a uniform magnetic field B. Let the angle between the direction of B and the perpendicular to the plane of the coil be \displaystyle \theta .
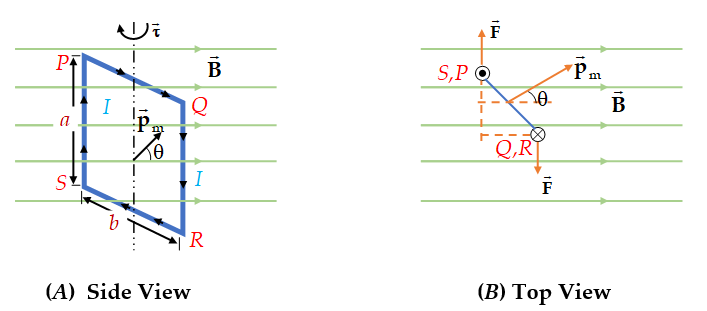
The element PQ experiences an upward force. The element RS experiences an equal force downward. So, the net force and torque due to these are zero. As shown in Fig. (B), the force on SP is equal and opposite to the force on QR. Each of these forces has magnitude IaB. Since these are not along the same line, a net torque is produced,
\displaystyle \tau = force x lever arm = BIa x b sin \displaystyle \theta
or \displaystyle \tau = BI(ab) sin \displaystyle \theta = (BIA sin \displaystyle \theta ) .where A = ab and it is the area of the loop.
For a loop of N turns the torque is given by \displaystyle \tau = (NBIA sin \displaystyle \theta ). Here NIA is the magnetic moment of the loop hence \displaystyle {{p}_{m}}=INA
The direction of the torque is such as to rotate the loop clockwise. The torque is fully defined by \displaystyle \tau ={{p}_{m}}B\sin \theta and in vector form \displaystyle \vec{\tau }={{\vec{p}}_{m}}\times \vec{B}, where \displaystyle {{{\vec{p}}}_{m}} is the magnetic moment having a direction perpendicular to the plane of the loop.
Practice Questions (Basic Level)
Q.1
A conducting circular loop of radius r carries a constant current I. It is placed in a uniform magnetic field \vec{B} such that \vec{B} is perpendicular to the plane of the loop. The magnetic force acting on the loop is
(a) BIr (b) 2 \displaystyle \pi IrB (c) zero (d) 2IrB
Ans. (c)
Q.2
A particle having mass m and charge q is attached to one end of a light rigid rod of length l. The rod is rotated at constant angular velocity about an axis normal to its length and passing through rod’s other free end. The ratio of the magnitude of the magnetic moment of the system and its angular momentum equals.
(a) \frac{q}{{2m}}
(b) \frac{1}{{m{{l}^{2}}}}
(c) \frac{q}{m}
(d) \frac{1}{{\pi m}}
Ans. (a)
Q.3
An insulating rod of length l carries a charge q distributed uniformly on it. The rod is pivoted at an end and is rotated at a frequency f about a fixed perpendicular axis. The magnetic moment of the system is
(a) zero
(b) \displaystyle \pi q f l2
(c) \frac{1}{2} \displaystyle \pi q f l2
(d) \frac{1}{3} \displaystyle \pi q f l2
Ans : (d)
4.
A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal to the coil. Calculate the magnitude of counter torque that must be applied to prevent the coil from turning.
(a) 3.25 Nm
(b) 3.14 Nm
(c) 3.00Nm
(d) 3.50 Nm
Ans (b)
5.
A coil in the shape of an equilateral triangle of side 0.02 m is suspended from a vertex such that it is hanging in a vertical plane between the pole pieces of a permanent magnet producing a horizontal magnetic field of 5\times {{10}^{{-2}}}T. Find the couple acting on the coil. When a current of 0.1 ampere is passed through it and the magnetic field is parallel to its plane.
(a) 7.5\times {{10}^{{-7}}}\,N-m
(b) 8.00\times {{10}^{{-7}}}\,N-m
(c) 8.66\times {{10}^{{-7}}}\,N-m
(d) 9.0\times {{10}^{{-7}}}\,N-m
Ans (c)
6.
A circular coil of 200 turns, radius 5 cm carries a current of 2.5 A. It is suspended vertically in uniform horizontal magnetic field of 0.25 T, with the plane of the coil making an angle of 60° with the field lines. Calculate the magnitude of ht torque that must be applied on it to prevent if from turning.
(a) 0.60 Nm
(b) 0.49 Nm
(c) 0.25 Nm
(d) 0.30 Nm
Ans (b)
Practice Questions (JEE Main Level)
Q.1
A rectangular loop carrying a current i is situated near a long, straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop. If a steady current I is established in the wire as shown in the figure the loop will
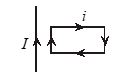
(a) rotate about an axis parallel to the wire
(b) move away from the wire
(c) move towards the wire
(d) Both (1) and (3)
Ans : (c)
Q.2
In the following figures which one correspond to the stable equilibrium position?
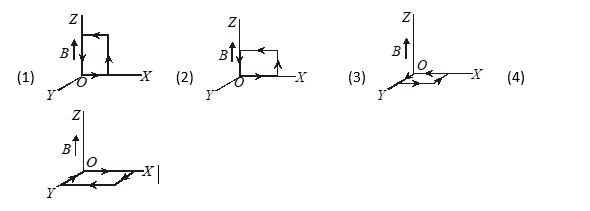
Ans : (3)
Q.3
A rectangular loop is placed in a vertical plane as shown in the figure. It has area A, and a current i is flowing through it in anticlockwise direction. Find the torque acting on it , if it is placed in a horizontal magnetic field B making an angle \theta with the loop.
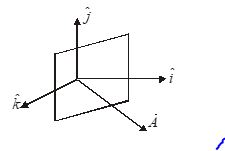
(a) B\,i\,A\,\hat{i}
(b) B\,i\,A\,\sin \theta \,\hat{k}
(c) B\,i\,A\,\cos \theta \,\hat{j}
(d) B\,i\,A\,\tan \theta \,\hat{k}
Ans : (c)
Q.4
A rectangular coil of size 3.0\,\,cm\times 4.0\,\,cm and having 100 turns is provided about the Z-axis as shown in figure. The coil carries an electric current of 2.0 A and a magnetic field of 1.0 T is present along the Y–axis. Find the torque acting on the coil if the side in the X–Y plane makes an angle \theta =37{}^\circ with the X–axis.
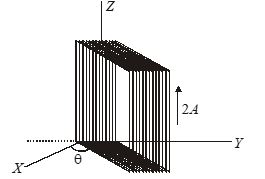
(a) 0.28 N – m
(b) 0.14 N – m
(c) 0.37 N – m
(d) 0.47 N – m
Ans. (b)
Q.5
An insulating rod of length l carries a charge q distributed uniformly on it. The rod is pivoted at an end and is rotated at a frequency f about a fixed perpendicular axis. The magnitude moment of the system is
(a) Zero
(b) \pi q\,f\,{{l}^{2}}
(c) \frac{1}{2}\pi q\,f\,{{l}^{2}}
(d) \frac{1}{3}\pi q\,f\,{{l}^{2}}
Ans. (d)
Q.6
The resistance of an ammeter of 1–ampere range is 1 ohm. Calculate the resistance of the shunt, which will increase the range of the ammeter to 10 amperes.
(a) \frac{1}{5}\,\,\Omega
(b) \frac{1}{9}\,\,\Omega
(c) \frac{1}{3}\,\,\Omega
(d) \frac{1}{15}\,\,\Omega
Ans (b)
Q.7
A voltmeter has got a resistance of . What alteration in it will have to be made so as to increase its range twenty times?
(a) 90000\,\,\Omega
(b) 85000\,\,\Omega
(c) 5000\,\,\Omega
(d) 95000\,\,\Omega
Ans (d)
Q.8.
A cyclotron’s oscillator frequency is 1 MHz. What should be the operating magnetic field for accelerating protons? If the radius of the Dees is 60 cm, what is the kinetic energy of the proton beam? {{m}_{p}}=1.67\times {{10}^{{-27}}}\,\,kg. Express your result in MeV (1 MeV=1.6\times {{10}^{{-13}}}\,\,J)
(a)0.60T, 7.2 MeV
(b)0.50T, 6.5 MeV
(c)0.66T, 7.4 MeV
(d)0.80T, 8.0 MeV
Ans (c)
Practice Questions (JEE Advance Level)
Q.1
A soft iron cylinder is used in a moving coil galvanometer, because without it
(a) The galvanometer will not work at all
(b) The magnetic field will not be uniformly radial
(c) The electric field will not be very strong
(d) The coil will not rest in position
Ans: (b)
Q.2
The magnetic field between the cylindrical pole piece used in the construction of the moving coil galvanometer is
(a) Rectangular throughout the space
(b) Rectangular only near the poles
(c) Radial through out the space
(d) Radial only near the poles
Ans : 4
Q.3
The sensitivity of a suspended type moving coil galvanometer will
(a) Increase if the length of the suspension wire is increased
(b) Decrease if the length is increased
(c) Remain unaffected by the change of the length of the suspension
(d) Increase if it is shortened
Ans (a)
Q.4
When a galvanometer coil of resistance G is shunted to send \frac{1}{n}th of the main current through it, the effective resistance of the galvanometer is
(a) nG
(b) (n-1)G
(c) \frac{G}{n}
(d) (n+1)G
Ans : (c)
Q.5
When a galvanometer of resistance g is shunted by a shunt S, the resistance of the circuit decreased by
(a) g-S
(b) \frac{{{{g}^{2}}}}{S}
(c) \frac{{{{g}^{2}}}}{{g+S}}
(d) \frac{g}{{g+S}}
Ans : (c)
Q.6
A radial field is purposely used in a moving coil galvanometer because
(a) Without it the galvanometer will not work at all.
(b) The galvanometer will work, but its deflection will not be proportional to the current
(c) The galvanometer will work and its deflection will be linearly proportional to the current
(d) The galvanometer will work, but its deflection will be proportional to \displaystyle \cos \theta , where \theta is the deflection of the coil
Ans : (c)
Q.7
To increase the range of an ammeter of resistance \gamma ohm n times, the shunt required is
(a) nr
(b) \frac{r}{n}
(c) \frac{r}{{n-1}}
(d) \frac{r}{{n+1}}
Ans : (c)
Q.8
A galvanometer can be converted into an ammeter by connecting
(a) A low resistance in series with it
(b) A low resistance in parallel to it
(c) A high resistance in series with
(d) A high resistance in parallel to it
Ans : (b)
Q.9
If 10% of the main current is to be passed through a moving coil galvanometer of resistance 99\,\,\Omega , then the required shunt resistance will be
(a) 9.9\,\,\Omega
(b) 10\,\,\Omega
(c) 11\,\,\Omega
(d) 9\,\,\Omega
Ans. (c)
Q.10
Choose the wrong statement. The sensitivity of a moving coil galvanometer can be increased by
(a) Increasing the number of turns in the coil
(b) Inserting a soft iron cylinder inside the coil
(c) Increasing the strength of the magnetic field
(d) Using a suspension fibre of a higher restoring couple per unit twist
Ans. (d)
Q.11
Co-ordinates of four corners of a square loop are A º (0, 0, 0), B º (0, 0, a),
C º \left( {\frac{a}{{\sqrt{2}}},\frac{a}{{\sqrt{2}}},a} \right) and D º \left( {\frac{a}{{\sqrt{2}}},\frac{a}{{\sqrt{2}}},0} \right). A current I is flowing in the loop in ABCDA direction. The magnetic moment of the loop would be
(a) \left( {\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{j}+\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{k}} \right)I
(b) \left( {\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{j}-\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{i}} \right)I
(c) \left( {\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{j}+\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{i}} \right)I
(d) \left( {\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{i}-\frac{{{{a}^{2}}}}{{\sqrt{2}}}\hat{j}} \right)I
Ans : (b)
