Video Lecture
Theory For Making Notes
Reflection of Wave
Whenever waves reflect at a boundary, it is possible for them to change phase. Figure, for example, shows that a wave on a string is inverted when it reflects from the end that is tied to a wall.In simple words a crest becomes a trough and a trough becomes a crest after the reflection with the wall (See the diagram, look at part 3 of the incident wave which is crest but after reflection it is converted into a trough).This inversion is equivalent to a half-cycle of the wave.

as if the wave had traveled an additional distance of one-half of a wavelength. In contrast, a phase change does not occur when a wave on a string reflects from the end of a string that is hanging free. When light waves undergo reflection, similar phase changes occur as follows:
(i) When light travels through a material with a smaller refractive index toward a material with a larger refractive index (e.g., air to gasoline or air to glass), reflection at the boundary occurs along with a phase change of p radians that is equivalent to one-half of a wavelength.
(ii) When light travels from a larger toward a smaller refractive index (e.g., glass to air), there is no phase change upon reflection at the boundary.
Colors In A Thin Film
Suppose the ray of light falling on the thin film of soapy water at A be incident at an angle i, as shown in figure.
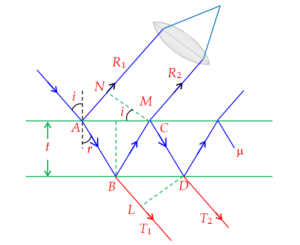
Let the thickness of the film be t and refractive index be \displaystyle \mu (> 1). At A it is partly reflected along \displaystyle A{{R}_{1}} giving the ray (1) and partly refracted along AB at an angle r. At B it is again partly reflected along BC and partly refracted along \displaystyle B{{T}_{1}}. Similar reflections and refractions occur at C. Since, the rays \displaystyle A{{R}_{1}} and \displaystyle C{{R}_{2}}, i.e. ray (1) and ray (2) have been derived from the same incident ray, they are coherent and in a position to interfere. If the set of parallel reflected rays is now collected by a lens, and focused at P, each ray has traveled a different distance, and the phase relationship between them may be such as to produce destructive or constructive interference at P. It is such interference that produces the colors of this film when seen by naked eyes.
Let CN and BM be perpendiculars to \displaystyle A{{R}_{1}} and AC. As the paths of the rays \displaystyle A{{R}_{1}} and \displaystyle C{{R}_{2}} beyond CN are equal, the path difference between ray (1) and (2) is given by
(path ABC in film-path AN in air)
therefore path difference = \displaystyle \mu (AB + BC) – AN … (1)
Here \displaystyle AB=BC=\frac{{BM}}{{\cos r}}=\frac{t}{{\cos r}},
and AN = AC sin i
Now AC = AM + MC = BM tan r + BM tan r
= 2t tan r
Also AN = 2t tan r sin i
\displaystyle =2t\frac{{\sin r}}{{\cos r}}(\sin i)
\displaystyle =2t\frac{{\sin r}}{{\cos r}}(\mu \sin r)
\displaystyle \left[ {\because \ \ \frac{{\sin i}}{{\sin r}}=\mu } \right]
\displaystyle =2\mu t\frac{{{{{\sin }}^{2}}r}}{{\cos r}}
Substituting these values of AB, BC and AN in Eq. (1) we get path difference
\displaystyle =\mu \left( {\frac{t}{{\cos r}}+\frac{t}{{\cos r}}} \right)-2\mu t\frac{{{{{\sin }}^{2}}r}}{{\cos r}}
\displaystyle =\frac{{2\mu t}}{{\cos r}}(1-{{\sin }^{2}}r)
hence path difference = 2 \displaystyle \mu t cos r
However, we must take account of the fact that ray (1) undergoes a phase change of \pi at reflection while ray (2) does not, since it is internally reflected . The phase change of \pi is equivalent to a path difference of \displaystyle \frac{\lambda }{2}. Hence, the effective path difference between ray (1) and rays (2) is
\displaystyle 2\mu t\cos r-\frac{\lambda }{2}
Now for constructive interference this path difference must be in integral multiple of \displaystyle \lambda . Hence
\displaystyle \begin{array}{l}\text{ }2\mu t\cos r-\frac{\lambda }{2}=n\lambda \\\Rightarrow \text{ }2\mu t\cos r=n\lambda +\frac{\lambda }{2}\end{array}
or \displaystyle 2\mu t\cos r=(2n+1)\frac{\lambda }{2}
So this becomes a condition for constructive interference as far as reflected rays ( \displaystyle {{R}_{1}}) and ( \displaystyle {{R}_{2}}) are concerned.
Whereas for transmitted rays \displaystyle {{T}_{1}} and \displaystyle {{T}_{2}} there is only one path difference between them which is \displaystyle 2\mu t\cos r and there is no extra path difference due to reflection.
Hence for constructive interference this path difference must be in integral multiple of wavelength \displaystyle \lambda . Hence
\displaystyle 2\mu t\cos r=n\lambda
So this becomes a condition for constructive interference as far as transmitted rays ( \displaystyle {{T}_{1}}) and ( \displaystyle {{T}_{2}}) are concerned.
Thus, when a thin film is illuminated by monochromatic light, and seen in reflected light, it appears bright or dark according to the path difference which is given as 2 \displaystyle \mu tcos(r) .
\displaystyle 2\mu t\cos r=(2n+1)\frac{\lambda }{2} (condition of maxima)
\displaystyle 2\mu t\cos r=n\lambda (condition of minima)
Conditions of Maxima and Minima for transmitted light
The rays emerging from the lower side of the film can also be brought together with a lens and made to interfere.
The path difference between the transmitted rays \displaystyle B{{T}_{1}} and \displaystyle D{{T}_{2}} is given by
(BC + CD) – BL = 2 \displaystyle \mu t cos r
In this case, film there are no phase change due to reflection at B or C, because in either case the light is traveling from denser to rarer medium. Hence, the effective path difference between \displaystyle B{{T}_{1}} and \displaystyle B{{T}_{2}} is also 2 \displaystyle \mu t cos r.
The two rays \displaystyle B{{T}_{1}} and \displaystyle D{{T}_{2}} reinforce each other, if 2 \displaystyle \mu t cos r = n \displaystyle \lambda (condition of maxima) where n = 1, 2, 3.
In this case, the film will appear bright in the transmitted light.
The two rays will destroy each other if
\displaystyle 2\mu t\cos r=(2n+1)\frac{\lambda }{2} (condition of minima)
where n = 0, 1, 2,…. and the film appears dark in transmitted light.
Hence we find that the conditions for the maxima and minima, in the reflected light are just the reverse of those in transmitted light. Therefore, only those colors will be visible in transmitted light, which were missed in reflected light. Hence, the film which appears bright in reflected light will appear dark in transmitted light and vice-versa. In other words, the appearances of colors in the two cases is complimentary to each other.
Reason of Colors in Reflection from a Thin Films
The sunlight consists of a continuous range of wavelengths (colors). At a particular point of the film, and for a particular position of the eye (i.e., for a particular t and a particular r), the rays of only certain wavelengths will have a path difference satisfying the condition of maxima. Hence, only these wavelengths (colors) will be present with the maximum intensity. While some others, which satisfy the condition of the minimum will be missing. Hence, the point of the film being viewed will appear colored.
Illustration
A thin film of \displaystyle 4\times {{10}^{{-5}}} cm thickness is illuminated by white light normal to its surface (r = \displaystyle 0{}^\circ ). Its refractive index is 1.5. Of what color will the thin film appear in reflected light? (Visible range 3500 – 7000 \displaystyle {{A}^{o}} )
Solution
The condition for constructive interference of light reflected, from a film is
\displaystyle 2\mu t\cos r=(2n+1)\frac{\lambda }{2},\ \text{where}\ n=0,1,2,….
Here \displaystyle \mu =1.5,
\displaystyle t=4\times {{10}^{{-5}}}\text{cm}\ \text{and}\ r=0{}^\circ (since light falls normally) so that cos r = 1.
therefore 2 × 1.5 × 4 × \displaystyle {{10}^{{5}}}= (2n + 1) \displaystyle \frac{\lambda }{2}
or \displaystyle \lambda =\frac{{4\times 1.5\times 4\times {{{10}}^{{-5}}}}}{{2n+1}} cm
or \displaystyle \lambda =\frac{{24\times {{{10}}^{{-5}}}}}{{2n+1}} cm
or \displaystyle \lambda =\frac{{24000}}{{2n+1}}{{A}^{o}}
Taking n = 0, 1, 2, 3, ….. we get different wavelengths.
For n=0 , \displaystyle \lambda =24000{{A}^{o}}
For n=1 , \displaystyle \lambda =8000{{A}^{o}}
For n=2 , \displaystyle \lambda =4800{{A}^{o}}
For n=3 , \displaystyle \lambda =3428{{A}^{o}}
These are the wavelengths reflected most strongly. Of these, the wavelength lying in the visible region is 4800 \displaystyle {\AA} (blue).
Interference by a Wedge-Shaped Film
Considering the interference pattern produced by a film of varying thickness, i.e., a film which is not plane-parallel. Observe that the interfering rays do not enter the eye parallel to each other but appear to diverge from a point near the film.
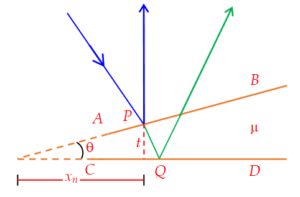
Let us consider a thin wedge-shaped film of refractive index m, bounded by two plane surfaces AB and CD, inclined at an angle \displaystyle \theta as shown in figure. Let the film be illuminated by a monochromatic source of light from a slit held parallel to the edge of the wedge (the edge is the line passing through the point O and perpendicular to the plane of the paper). Interference occurs between the rays reflected at the upper and lower surfaces of the film. In this case the path difference for a given pair of rays is practically that given by equation \displaystyle 2\mu t\text{ }cosr. But, if it is assumed that light is incident almost normally at a point P on the film, the factor cos r may be considered equal to 1. Thus the path difference between the rays reflected at the upper and lower surfaces is \displaystyle 2\mu t, where t is the thickness of the film at P. An additional path difference of \displaystyle \frac{\lambda }{2} is introduced in the ray reflected, from the upper surface. The effective path difference between the two rays is
\displaystyle 2\mu t-\frac{\lambda }{2}
Hence the condition for bright fringes becomes
\displaystyle 2\mu t-\frac{\lambda }{2}=n\lambda
or \displaystyle 2\mu t=(2n+1)\frac{\lambda }{2}
The condition for dark fringe is
\displaystyle 2\mu t=n\lambda
It is clear that for a bright or dark fringe of a particular order, t must remain constant. Since in the case of a wedge-shaped film, t remains constant along lines parallel to the thin edge of the wedge, the bright and dark fringes are straight lines parallel to the thin edge of the wedge. Such fringes are commonly referred to as ‘‘fringes of equal thickness’’. At the thin edge, where t = 0, path difference \displaystyle =\frac{\lambda }{2} , which is a condition for minimum intensity. Hence, the edge of the film is dark. The resulting fringes resemble the localized fringes in the Michelson interferometer (this you will study in next unit) and appear to be formed in the film itself.
Spacing between Two Consecutive Bright (or Dark) Fringes :
For the nth dark fringe, we have \displaystyle 2\mu t\text{ }=\text{ }n\lambda
Let this fringe be obtained at a distance \displaystyle {{x}_{n}} from the thin edge. Then \displaystyle t={{x}_{n}}tan\theta ={{x}_{n}}\theta (when \displaystyle \theta is small and measured in radians).
therefore \displaystyle 2\mu {{x}_{n}}\theta =n\lambda
Similarly, if the (n + 1)th dark fringe is obtained at a distance \displaystyle {{x}_{{n+1}}} from the thin edge, then
\displaystyle 2\mu {{x}_{{n+1}}}\theta =(n+1)\lambda
Subtracting two equations we get
\displaystyle 2\mu \theta ({{x}_{{n+1}}}-{{x}_{n}})=\lambda
Hence the fringe width \displaystyle \omega is
\displaystyle \omega ={{x}_{{n+1}}}-{{x}_{n}}=\frac{\lambda }{{2\mu \theta }}
where \displaystyle \theta is measured in radians.
Similarly, it can be shown that the spacing between two consecutive bright fringes (fringe width) is abo \displaystyle \frac{\lambda }{{2\mu \theta }}.
Lloyd’s Mirror Experiment
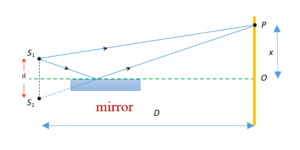
Similar to YDSE the path difference between the rays from \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} at P is given by \displaystyle \Delta x=\frac{{xd}}{D}, But due to a phase change of \displaystyle \pi which occurs when light is reflected from a denser medium(mirror) the total path difference becomes
\displaystyle \Delta x=\frac{{xd}}{D}+\frac{\lambda }{2}
For the constructive interference this path difference should be \displaystyle n\lambda .
Hence \displaystyle \frac{{xd}}{D}+\frac{\lambda }{2}=n\lambda
\displaystyle \Rightarrow \text{ }\frac{{xd}}{D}=n\lambda -\frac{\lambda }{2}
\displaystyle \Rightarrow \text{ }\frac{{xd}}{D}=(2n-1)\frac{\lambda }{2}
hence \displaystyle x=(2n-1)\frac{{\lambda D}}{{2d}} This is the position of bright fringes which is just opposite to that of YDSE.
Thus, whenever there exists a phase difference of a \displaystyle \pi between the two interfering beams of light, conditions of maximas and minimas are interchanged.
At grazing incidence a fringe is formed at O, where the geometrical path difference between the direct and reflected waves is zero but due to a phase change of \displaystyle \pi as discussed above it will be a dark fringe rather than bright.
Illustration
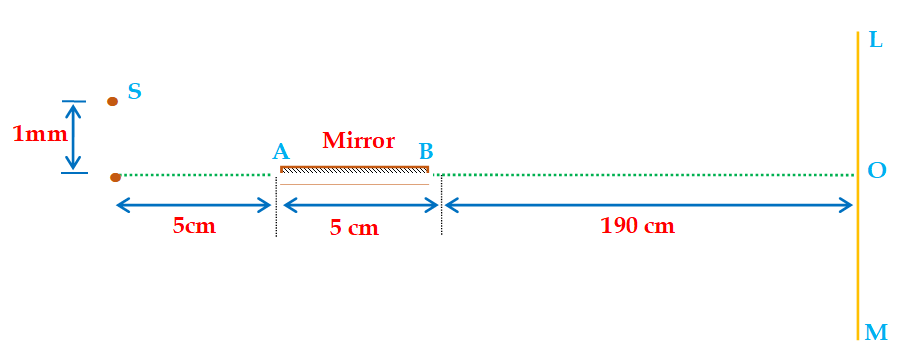
The arrangement of the Lloyd’s mirror experiment is shown in the figure. ‘S’ is a point source of frequency \displaystyle 6~\times {{10}^{{14}}}Hz. A and B represent the two ends of a mirror placed horizontally, and LOM represents the screen.Determine the position of the region where the fringes will be visible and calculate the number of fringes.
Solution
Using geometry,
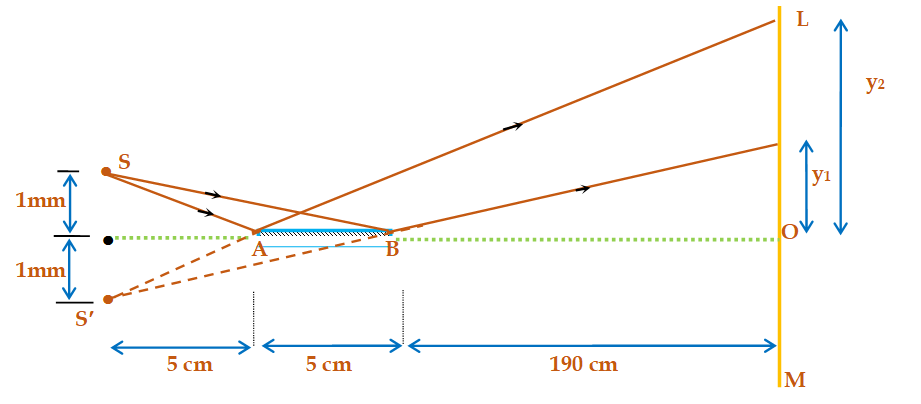
\displaystyle {{y}_{1}} = (190) \displaystyle \frac{{0.1}}{{10}}=1.9cm and \displaystyle {{y}_{2}} = (195) \displaystyle \frac{{(0.1)}}{5}=3.9cm
The region in which interference occurs is \displaystyle {{y}_{2}}-\text{ }{{y}_{1}} = 3.9-1.9 = 2cm
The fringe width is
\omega =\frac{{\lambda D}}{{2d}}
Where D = 190 + 5 + 5 = 200 cm ; 2d = 2mm
\displaystyle \lambda =\frac{c}{\nu }=\frac{{3\times {{{10}}^{8}}}}{{6\times {{{10}}^{{14}}}}}=0.5\mu m
\displaystyle \therefore \omega =\left( {0.5\times {{{10}}^{{-6}}}} \right)\left( {\frac{{2000}}{2}} \right)=0.5mm
no.of fringes = \displaystyle \frac{{\left( {{{y}_{2}}-{{y}_{1}}} \right)}}{\omega } = \displaystyle \frac{{\left( {20} \right)}}{{0.5}}=40.
Where D = 190 + 5 + 5 = 200 cm ; 2d = 2mm
\displaystyle \lambda =\frac{c}{\nu }=\frac{{3\times {{{10}}^{8}}}}{{6\times {{{10}}^{{14}}}}}=0.5\mu m
\displaystyle \therefore \omega =\left( {0.5\times {{{10}}^{{-6}}}} \right)\left( {\frac{{2000}}{2}} \right)=0.5mm
no.of fringes = \displaystyle \frac{{\left( {{{y}_{2}}-{{y}_{1}}} \right)}}{\omega } = \displaystyle \frac{{\left( {20} \right)}}{{0.5}}=40.
Fresnel’s Bi-prism Experiment
It is an optical device of producing interference of light Fresnel’s biprism is made by joining base to base two thin prism of very small angle. The acute angle of prism is about \displaystyle 1/{{2}^{o}} and obtuse angle of prism is about \displaystyle {{179}^{o}}. When a monochromatic light source is kept in front of biprism two virtual images are formed at \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} which acts as coherent virtual source .Interference fringes are found on the screen placed behind the biprism interference fringes are formed in the limited region which can be observed with the help eye piece.
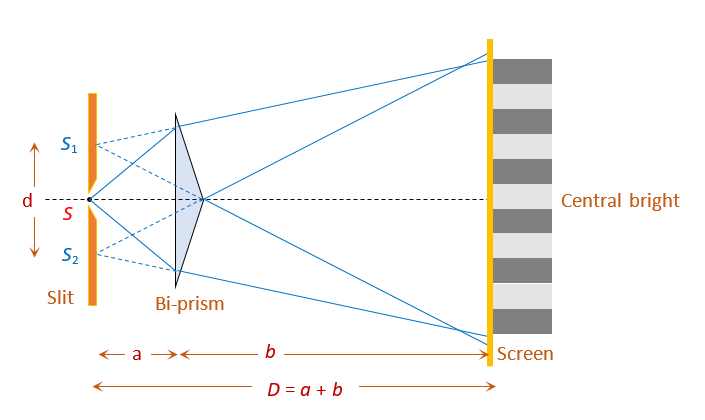
Let the separation between \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} be d and the distance of slits and the screen from the biprism be a and b respectively i.e. D = (a + b). The relation for the fringe width is same as that of the YDSE i.e. \omega =\frac{{\lambda \,D}}{d}If angle of prism is \displaystyle \alpha and refractive index is \displaystyle \mu then d=2a(\mu -1)\alpha (See concept of thin prism in ray optics)
\ \omega =\frac{{(a+b)\lambda }}{{2a(\mu -1)\alpha }}
Normally the fringe width is measured by a micrometer attached to the eye piece. Fringes are of equal width
If a convex lens is mounted between the biprism and screen or eye piece. There will be two positions of lens when the sharp images of coherent sources \displaystyle {{S}_{1}} and \displaystyle {{S}_{2}} will be observed in the eyepiece.(See Displacement method of finding focal length of a lens in Ray Optics)
The separation of the images in the two positions are measured. Let these be \displaystyle {{d}_{1}} and \displaystyle {{d}_{2}} then d=\sqrt{{{{d}_{1}}{{d}_{2}}}}
\ \lambda =\frac{{\omega d}}{D}
hence \lambda=\frac{{\omega \sqrt{{{{d}_{1}}{{d}_{2}}}}}}{{(a+b)}}.
Illustration
In Fresnel’s biprism (\mu =1.5) experiment the distance between source and biprism is 0.3 m and that between biprism and screen is 0.7m and angle of prism is \displaystyle {{1}^{o}}. Find the fringe width with light of wavelength 6000 \displaystyle {\AA}.
Solution
We know that
\omega =\frac{{(a+b)\lambda }}{{2a(\mu -1)\alpha }}
where a = distance between source and biprism = 0.3 m
b = distance between biprism and screen = 0.7 m.
\displaystyle \alpha = Angle of prism = \displaystyle {{1}^{o}}.,
(\mu =1.5) ,
\lambda = 6000 ´ \displaystyle {{10}^{{-10}}}m
Hence, \omega =\frac{{(0.3+0.7)\times 6\times {{{10}}^{{-7}}}}}{{2\times 0.3(1.5-1)\times ({{1}^{o}}\times \frac{\pi }{{180}})}}
= 1.14 ´ \displaystyle {{10}^{{-4}}}m = 0.0114 cm.
Newton’s Ring
If we place a plano-con vex lens on a plane glass surface, a thin film of air is formed between the curved surface of the lens and plane glass plate. If we allow monochromatic light to fall normally on the surface of lens, then circular interference fringes of radius r can be seen in the reflected light. This circular fringes are called Newton rings.
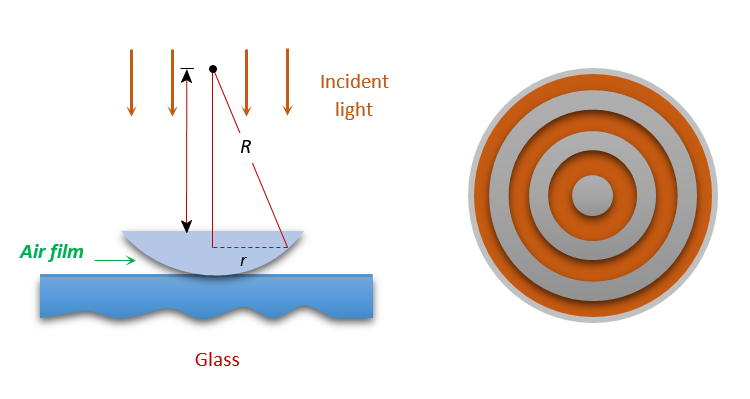
The central fringe is a dark spot then there are alternate bright and dark fringes (Ring shape). Radius of \displaystyle {{n}^{{th}}} dark ring {{r}_{n}}=\,\sqrt{{n\lambda R}} where n = 0, 1, 2, ….., R = Radius of convex surface
Whereas the radius of \displaystyle {{n}^{{th}}} bright ring is given by {{r}_{n}}=\sqrt{{\left( {n-\frac{1}{2}} \right)\lambda R}} , where n = 1, 2, 3,…..
If a liquid of refractive index \mu is introduced between the lens and glass plate, the radii of dark ring would be {{r}_{n}}=\sqrt{{\frac{{n\lambda R}}{\mu }}}.
Newton’s ring arrangement is used of determining the wavelength of monochromatic light.
For this the diameter of \displaystyle {{n}^{{th}}} dark ring ( \displaystyle {{D}_{{n}}}) and \displaystyle {{n+m}^{{th}}} dark ring ( \displaystyle {{D}_{{n+m}}}) are measured
Since \displaystyle {{D}_{{(n)}}}=2{{r}_{n}}
\displaystyle \therefore {{D}_{{(n)}}}=2\sqrt{{n\lambda R}}
hence \displaystyle D_{(n)}^{2}=4n\lambda R
similarly D_{{(n+m)}}^{2}=4(n+m)\lambda R
subtracting two we can find the wavelength
hence
\displaystyle D_{{(n+m)}}^{2}-D_{(n)}^{2}=4(n+m)\lambda R-4n\lambda R
or \displaystyle D_{{(n+m)}}^{2}-D_{(n)}^{2}=4m\lambda R
therefore \displaystyle \lambda =\frac{{D_{{(n+m)}}^{2}-D_{(n)}^{2}}}{{4mR}}
Practice Questions (Basic Level)
1.
Soap bubble appears coloured due to the phenomenon of
(a) Interference
(b) Diffraction
(c) Dispersion
(d) Reflection
Ans (a)
2.
On a rainy day, a small oil film on water show brilliant colours. This is due to
(a) Dispersion of light
(b) Interference of light
(c) Absorption of light
(d) Scattering of light
Ans (b)
3.
The phase difference between incident wave and reflected wave is 180° when light ray
(a) Enters into glass from air
(b) Enters into air from glass
(c) Enters into glass from diamond
(d) Enters into water from glass
Ans (a)
4.
What causes changes in the colours of the soap or oil films for the given beam of light
(a) Angle of incidence
(b) Angle of reflection
(c) Thickness of film
(d) None of these
Ans (c)
5.
In Fresnel’s biprism (\mu =1.5) experiment the distance between source and biprism is 0.3 m and that between biprism and screen is 0.7m and angle of prism is 1°. The fringe width with light of wavelength 6000 Å will be
(a) 3 cm
(b) 0.011 cm
(c) 2 cm
(d) 4 cm
Ans (b)
6.
In Fresnel’s biprism experiment, on increasing the prism angle, fringe width will
(a) Increase
(b) Decrease
(c) Remain unchanged
(d) Depend on the position of object
Ans (b)
7.
If prism angle \alpha =1{}^\circ ,\ \mu =1.54,distance between screen and prism (b)=0.7\,m, distance between prism and source a=0.3\,m,\ \lambda =180\pi \ nm then in Fresnal biprism find the value of \beta (fringe width)
(a) {{10}^{{-4}}}m
(b) {{10}^{{-3}}}mm
(c) {{10}^{{-4}}}\times \pi m
(d) \pi \times {{10}^{{-3}}}m
Ans (a)
8.
If Fresnel’s biprism experiment as held in water inspite of air, then what will be the effect on fringe width
(a) Decrease
(b) Increase
(c) No effect
(d) None of these
Ans (a)
9.
What is the effect on Fresnel’s biprism experiment when the use of white light is made
(a) Fringe are affected
(b) Diffraction pattern is spread more
(c) Central fringe is white and all are coloured
(d) None of these
Ans (c)
10.
In which of the following is the interference due to the division of wave front
(a) Young’s double slit experiment
(b) Fresnel’s biprism experiment
(c) Lloyd’s mirror experiment
(d) Demonstration colours of thin film
Ans (b)
Practice Questions (JEE Main Level)
1.
A glass plate of refractive index 1.5 is coated with a thin layer of thickness t and refractive Index 1.8. Light of wavelength \displaystyle \lambda travelling in air is incident normally on the layer . It is partly reflected at the upper and the lower surfaces of the layer and the two reflected rays interfere. If \displaystyle \lambda = 648 nm, obtain the least value of t for which the rays interfere constructive
(a) 45 nm
(b) 90 nm
(c) 180 nm
(d) 135 nm
7.
In an air wedge experiment, monochromatic light of wavelength 500 nm is incident normally on the upper plate. When viewed from above, the distance of the centre of the fifth bright fringe from O is
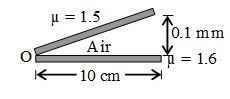
(a) 1.125 mm
(b) 1 mm
(c) 1.63 mm
(d) none of these
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
