Video Lecture
Theory For Making Notes
Lens Makers Formula
Lens Maker’s formula is a relation that connects focal length of a lens to radii of curvature of the two surfaces of the lens and refractive index of the material of the lens.
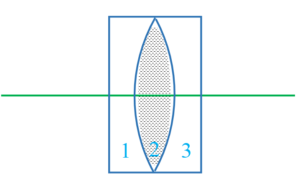
Consider a convex lens as shown in figure. \displaystyle {{P}_{1}}, \displaystyle {{P}_{2}} are the poles, \displaystyle {{C}_{1}}, \displaystyle {{C}_{2}} are the centers of curvature of two surfaces of a thin convex lens XY with optical centre of lens. Let \displaystyle {{\mu }_{2}} be the refractive index of the material of the lens and \displaystyle {{\mu }_{1}} be the refractive index of the rarer medium around the lens.
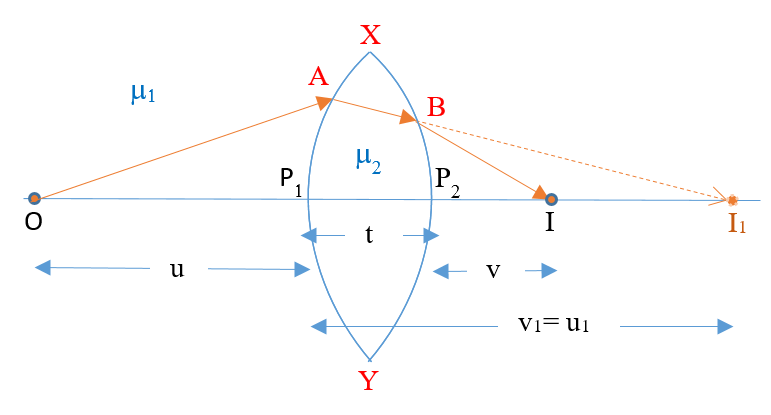
Consider a point object O lying on the principle axis of the lens. A ray of light starting from O and incident normally on the surface \displaystyle X{{P}_{1}}Y along \displaystyle O{{P}_{1}} passes straight. Another ray incident on \displaystyle X{{P}_{1}}Y along OA is refracted along AB. If the lens material were continuous and there were no boundary/second surface \displaystyle X{{P}_{2}}Y of the lens, the refracted ray AB would go straight meeting the first refracted ray at \displaystyle {{I}_{1}}. Therefore, \displaystyle {{I}_{1}} would have been a real image of O formed after refraction at \displaystyle X{{P}_{1}}Y.
If {{P}_{1}}{{I}_{1}}={{v}_{1}} and {{P}_{1}}O=u,
From the formula of spherical surface we get
\frac{{{{\mu }_{1}}}}{{-u}}+\frac{{{{\mu }_{2}}}}{{{{v}_{1}}}}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{{{{R}_{1}}}} …(i)
Actually, the lens material is not continuous. Therefore, the refracted ray AB suffers further refraction at B and emerges along BI, meeting actually the principle axis at I. Therefore, I is the final real image of O, formed after refraction thought the convex lens.
For refraction at the second surface \displaystyle X{{P}_{2}}Y, we can regard \displaystyle {{I}_{1}} as a virtual object, whose real image is formed at I.
Therefore, for second surface u={{v}_{1}},
Let \displaystyle {{R}_{2}}Y be radius of curvature of second surface of the lens.
As refraction is now taking place from denser to rarer medium, therefore, using equation of spherical surface , we get
\frac{{-{{\mu }_{2}}}}{{{{v}_{1}}}}+\frac{{{{\mu }_{1}}}}{v}=\frac{{{{\mu }_{1}}-{{\mu }_{2}}}}{{{{R}_{2}}}}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{{-{{R}_{2}}}} …(ii)
Adding (i) and (ii), we get
\frac{{{{\mu }_{1}}}}{{-u}}+\frac{{{{\mu }_{1}}}}{v}=({{\mu }_{2}}-{{\mu }_{1}})\ \left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
or
{{\mu }_{1}}\left[ {\frac{1}{v}-\frac{1}{u}} \right]=({{\mu }_{2}}-{{\mu }_{1}})\ \left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
or
\frac{1}{v}-\frac{1}{u}=\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}-1} \right)\ \left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right) …(iii)
Put \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}=\mu = refractive index of material of the lens w.r.t. surrounding medium.
When object on the left of lens is at \displaystyle \infty , image is formed at the principal focus of the lens
therefore when u = \displaystyle \infty , then v = f = focal length of the lens.
From (iii),
\frac{1}{f}-\frac{1}{\infty }=(\mu -1)\ \left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
or \displaystyle \frac{1}{f}=(\mu -1)\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right) .
(This is called thin lens or lens maker’s formula)
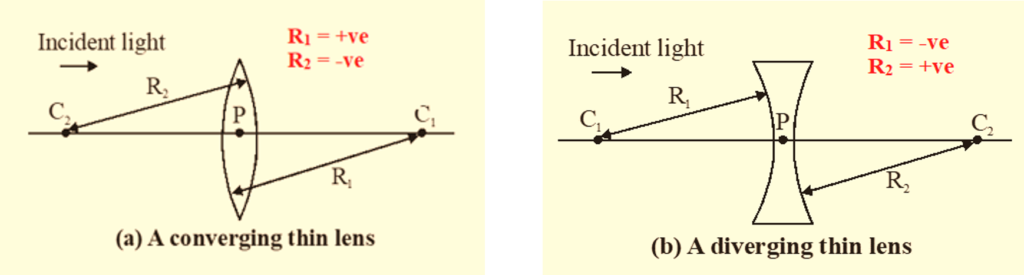
While using this formula take care of the sign of the radius of curvature \displaystyle {{R}_{1}} and \displaystyle {{R}_{2}}
The line joining \displaystyle {{C}_{1}} and \displaystyle {{C}_{2}} is called the principal axis of the lens. The centre P of the thin lens which lies on the principal axis, is called the optical centre.
Focus:
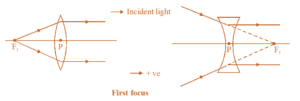
Unlike a mirror, a lens has two foci.
First focus ( \displaystyle {{F}_{1}}): It is defined as a point at which if an object (real in case of a convex lens and virtual for concave) is placed, the image of this object is formed at infinity. Or we can say, rays passing through \displaystyle {{F}_{1}} become parallel to the principal axis after refraction from the lens. The distance \displaystyle P{{F}_{1}} is the first focal length \displaystyle {{f}_{1}} .
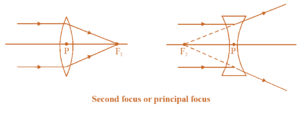
Second focus or principal focus ( \displaystyle {{F}_{2}}): A narrow beam of light travelling parallel to the principal axis either converge (in case of a convex lens) or diverge (in case of a concave lens) at a point \displaystyle {{F}_{2}} after refraction from the lens. This point \displaystyle {{F}_{2}} is called the second or principal focus. If the rays converge at \displaystyle {{F}_{2}}, the lens is said a converging lens and if they diverge, they are called diverging lens. Distance \displaystyle P{{F}_{2}} is the second focal length \displaystyle {{f}_{2}}.
Change of focal length of a lens
When a lens (convex lens say) is kept in air then the focal length is given as
\displaystyle \frac{1}{{{{f}_{{air}}}}}=\left( {{{\mu }_{l}}-1} \right)\,\,\left( {\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}} \right) –(A)
(a) When a lens (convex lens say) is kept in any medium other than air of R.I. = \displaystyle {{\mu }_{m}}
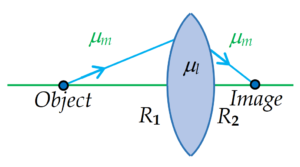
In that case the focal length is given as
\displaystyle \frac{1}{{{{f}_{m}}}}=\left( {\frac{{{{\mu }_{l}}}}{{{{\mu }_{m}}}}-1} \right)\,\,\left( {\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}} \right)
or
\displaystyle \frac{1}{{{{f}_{m}}}}=\left( {\frac{{{{\mu }_{l}}-{{\mu }_{m}}}}{{{{\mu }_{m}}}}} \right)\,\,\left( {\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}} \right) –(B)
dividing equation (A) and (B) we get
\displaystyle \frac{{{{f}_{m}}}}{{{{f}_{a}}}}=\left( {\frac{{{{\mu }_{l}}-1}}{{{{\mu }_{l}}-{{\mu }_{m}}}}} \right)\,
\displaystyle \Rightarrow \text{ }{{f}_{m}}=\left( {\frac{{{{\mu }_{l}}-1}}{{{{\mu }_{l}}-{{\mu }_{m}}}}} \right)\,{{f}_{a}}
Case I :
When the refractive index of the medium is less than that of the lens
\displaystyle {{\mu }_{m}}<{{\mu }_{l}}
using the above equation i.e. \displaystyle \text{ }{{f}_{m}}=\left( {\frac{{{{\mu }_{l}}-1}}{{{{\mu }_{l}}-{{\mu }_{m}}}}} \right)\,{{f}_{a}}
hence \displaystyle {{f }_{m}}>{{f}_{a}} and \displaystyle {{P }_{m}}<{{P}_{a}}
Therefore the focal length increases, consequently the power of the lens decreases. The nature of the lens remains unchanged,
Case II:
When the refractive index of the medium is equal to that of the lens,
i.e. \displaystyle {{\mu }_{m}}={{\mu }_{l}}
using the above equation i.e. \displaystyle \text{ }{{f}_{m}}=\left( {\frac{{{{\mu }_{l}}-1}}{{{{\mu }_{l}}-{{\mu }_{m}}}}} \right)\,{{f}_{a}}
hence \displaystyle {{f}_{m}}=\infty
and \displaystyle {{P}_{m}}=\frac{1}{{{{f}_{m}}}}=0
Therefore, the focal length of the lens becomes infinity and the power becomes zero. Consequently, the lens behaves like a glass slab plate.
Case III:
When the refractive index of the medium is greater than that of the lens,
\displaystyle {{\mu }_{m}}>{{\mu }_{l}}
using the above equation i.e. \displaystyle \text{ }{{f}_{m}}=\left( {\frac{{{{\mu }_{l}}-1}}{{{{\mu }_{l}}-{{\mu }_{m}}}}} \right)\,{{f}_{a}}
hence \displaystyle {{f}_{m}}<{{f}_{a}} and \displaystyle {{P}_{m}}\,>{{P}_{a}}
Therefore the focal length of the lens decreases. Consequently the power of the lenses increases numerically.
Since \displaystyle {{\mu }_{m}}>{{\mu }_{l}}
hence \displaystyle {{\mu }_{l}}-{{\mu }_{m}}<0
therefore \displaystyle {{f}_{m}} is negative
The negative focal length means that, the nature of the lens changes from converging to diverging and vice versa.
Few Importants Points:
(a)
When the lens has an air bubble, its focal length increases and power decreases, An air bubble in water, behaves as a divergent lens.
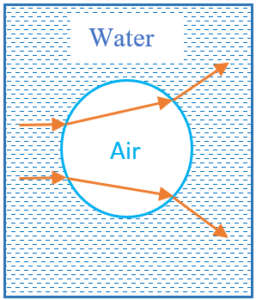
(b)
When a bi (equi) convex lens is cut transversely into two equal parts the radius of curvature of the lens in the cutting side increases to infinity. Now the focal length f increases to twice the previous value.
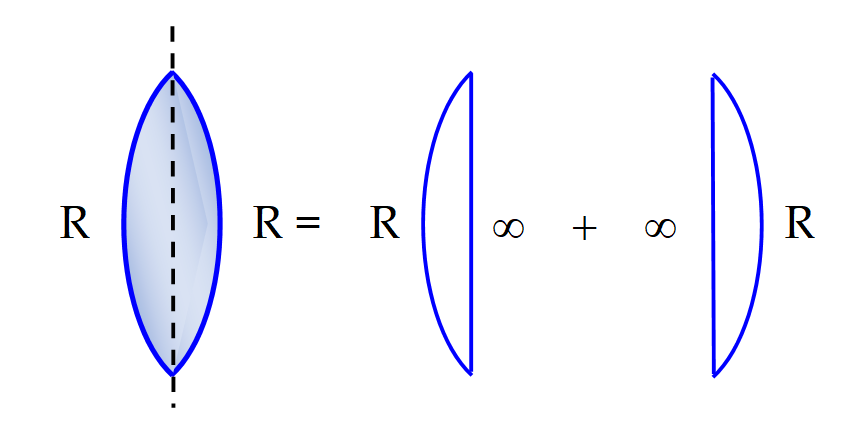
(c)
When a lens is cut into two equal halves parallel to principal axis, the focal length of each part remains same as that of initial lens.
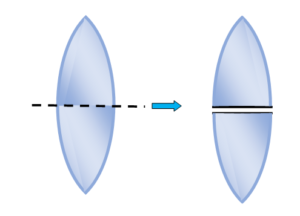
Illustration
Calculate the focal length of a biconvex lens in air if the radii of its surfaces are 60 cm and 15 cm. Refractive index of glass = 1.5
Solution
Consider a light ray going through the lens as shown. It strikes the convex side of 60 cm radius and concave side of 15 cm radius while coming out.
\displaystyle {{R}_{1}} = + 60 cm
\displaystyle {{R}_{2}} = – 15 cm
as we know
\frac{1}{f}\,=\,\left[ {\,\frac{\mu }{{{{\mu }_{0}}}}-1} \right]\,\,\left[ {\frac{1}{{{{R}_{1}}}}\,-\,\frac{1}{{{{R}_{2}}}}} \right]
or, \frac{1}{f}\,=\,\left[ {\frac{{1.5}}{1}-1} \right]\,\,\left[ {\frac{1}{{60}}+\frac{1}{{15}}} \right]
hence f = + 24 cm
Illustration
Calculate the focal length of a concave lens in water ( \displaystyle {{\mu }_{w}}= 4/3) if the surface have radii equal to 40 cm and 30 cm. \displaystyle {{\mu }_{g}}= 1.5
Solution
\displaystyle {{R}_{1}} = 30 cm;
\displaystyle {{R}_{2}} = + 40 cm
we have \frac{1}{f}\,=\,\left( {\frac{\mu }{{{{\mu }_{0}}}}-1} \right)\,\left[ {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right]
= \left[ {\frac{{1.5}}{{4/3}}-1} \right]\,\,\left[ {\frac{1}{{-30}}\,-\,\frac{1}{{40}}} \right]
hence f = – \frac{{960}}{7} = – 137.1 cm
Illustration
A plane convex lens has a focal length 12 cm and is made up of glass with refractive index 1.5. Find the radius of curvature of its curved side.
Solution
Let x = magnitude of the radius of curvature
Let \displaystyle {{R}_{1}} = + x ,
And \displaystyle {{R}_{2}} = \infty
We have \frac{1}{f} = \left( {\frac{\mu }{{{{\mu }_{0}}}}-1} \right)\,\,\left[ {\frac{1}{{{{R}_{1}}}}\,-\,\frac{1}{{{{R}_{2}}}}} \right]
or \frac{1}{{+12}}= \left( {\frac{{1.5}}{1}-1} \right)\,\,\left[ {\frac{1}{x}\,-\,\frac{1}{\infty }} \right]
or \frac{1}{{+12}}\,=\,(.5)\,\times \,\,\frac{1}{x}
hence x = 6 cm
Illustration
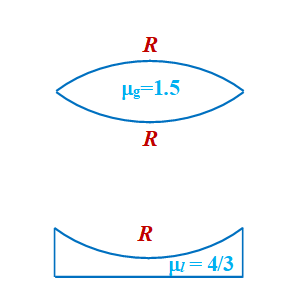
Two plano-concave lens of glass of refractive index 1.5 have radii of curvature 20 cm and 30 cm. They are placed in contact with curved surfaces towards each-other and the space between them is filled with a liquid of refractive index 4/3. Find the focal length of the system.
Solution
As shown in figure, the system is equivalent to combination of three lenses in contact,
Hence the resultant focal length F is given by
\frac{1}{F}\,=\,\frac{1}{{{{f}_{1}}}}\,+\,\frac{1}{{{{f}_{2}}}}\,+\,\frac{1}{{{{f}_{3}}}}
By lens maker’s formula
\frac{1}{{{{f}_{1}}}}\,=\,\left( {\frac{3}{2}-1} \right)\,\,\left[ {\frac{1}{\infty }\,-\,\frac{1}{{20}}} \right]\,=\,\frac{1}{{40}} cm
\frac{1}{{{{f}_{2}}}}\,=\,\left( {\frac{4}{3}-1} \right)\,\left[ {\frac{1}{{20}}-\frac{1}{{-30}}} \right]\,\,=\,\frac{5}{{180}} cm
\frac{1}{{{{f}_{3}}}}\,=\,\left( {\frac{3}{2}-1} \right)\,\,\left[ {\frac{1}{{-30}}\,-\,\frac{1}{\infty }} \right]\,\,=\,-\frac{1}{{60}} cm
therefore \frac{1}{F}\,=\,-\frac{1}{{40}}\,\,+\,\frac{5}{{180}}\,-\,\frac{1}{{60}}
hence F = – 72 cm
Thus, the system will behave as a concave lens of focal length 72 cm.
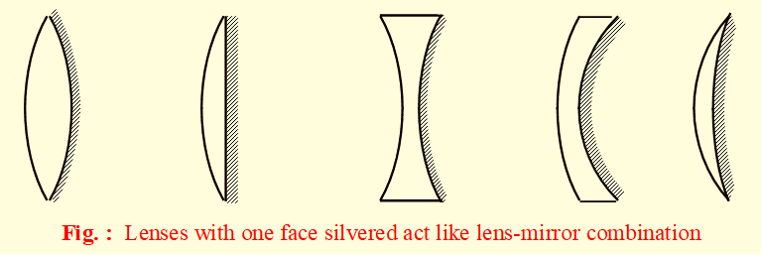
Lens with one surface silvered
When one face of a lens is silvered (as shown in figure) it acts like a lens-mirror combination.
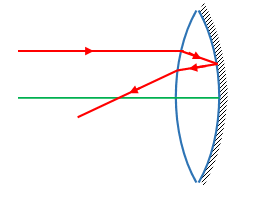
It is obvious from the ray diagram (as shown in figure) that the incident ray of light is refracted through the lens twice (i.e., once when light is incident on the lens and second time when reflected by the mirror) and reflected from the mirror once.
When one surface of a thin lens is silvered, the rays are reflected back at this silvered surface.
The combination acts like a spherical mirror whose equivalent focal length is given by adding powers of lens and mirror.
P={{P}_{{lens}}}+{{P}_{{mirror}}}+{{P}_{{lens}}}
Power of lens is taken two times because the light ray passes through the lens two times, one before reaching the mirror and second after reflection.
Replacing power by \frac{1}{f}\,we get
\frac{1}{F}=\frac{1}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}+\frac{1}{{{{f}_{l}}}}=\frac{2}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}
where \displaystyle {{f}_{l}} = focal length of lens and
\displaystyle {{f}_{m}} = focal length of mirror
F = Resultant focal length of the spherical mirror formed due to silvering of lens.
Sign convention
In the above formula, the focal length of the converging lens or mirror is positive; and that of diverging lens or mirror is negative.
Illustration
One face of an equiconvex lens of focal length 60 cm made of glass (m = 1.5) is silvered. Does it behave like a concave mirror or convex mirror?
Solution
Let x be the radius of curvature of each surface.
\frac{1}{{60}}\,=\,(1.5-1)\,\left[ {\frac{1}{x}-\,\frac{1}{{-x}}} \right]

or, \frac{1}{{60}}\,=\,-5\,\times \,\frac{2}{x}
hence x = 60 cm
Let F be the focal length of the equivalent spherical mirror,
Then
\frac{1}{F}\,=\,\frac{1}{{{{f}_{l}}}}\,+\,\frac{1}{{{{f}_{m}}}}\,\,+\,\frac{1}{{{{f}_{{_{l}}}}}}
or, \frac{1}{F}\,=\,\frac{2}{{{{f}_{{_{l}}}}}}\,+\,\frac{1}{{{{f}_{m}}}}
Here, \displaystyle {{f}_{l}} = + 60 cm (convex lens),
\displaystyle {{f}_{m}} = \frac{R}{2} = + 30 cm (concave mirror)
\frac{1}{F}\,=\,\frac{2}{{60}}+\,\frac{1}{{30}}\,=\,\frac{2}{{30}}
F = + 15 cm
Illustration
The plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
Solution
Let f be the focal length of the equivalent spherical mirror.
we have \frac{1}{F}\,=\,\frac{1}{{{{f}_{{_{l}}}}}}\,+\,\frac{1}{{{{f}_{m}}}}\,+\,\frac{1}{{{{f}_{l}}}}
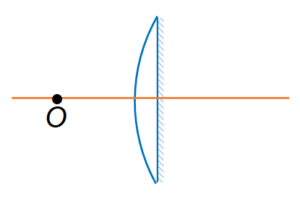
or, \frac{1}{F}\,=\frac{2}{{{{f}_{{_{l}}}}}}\,+\,\frac{1}{{{{f}_{m}}}}
Here, \displaystyle {{f}_{l}} = + 60 cm
\displaystyle {{f}_{m}} = \infty
\frac{1}{F}\,=\,\frac{2}{{60}}\,+\,\frac{1}{\infty }\,=\,\frac{1}{{30}}
or F = + 30 cm
The problem is reduced to a simple case where a point object is placed in front of a concave mirror.
Now, using the mirror formula
\frac{1}{u}\,+\,\frac{1}{v}\,=\,\frac{1}{f},
we have \frac{1}{{-20}}\,+\,\frac{1}{v}\,=\,\frac{1}{{-30}}
hence v = 60 cm
The image is erect and virtual.
Illustration
One face of an equiconvex lens of focal length 60 cm made of glass ( \displaystyle \mu = 1.5) is silvered . Does it behave like a concave mirror or convex mirror?
Solution
Applying lens makers formula, the radius of curvature of the equiconvex lens
From equation
\frac{1}{F}=\frac{2}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}
here \displaystyle {{f}_{l}} = +60cm (converging lens)
and \displaystyle {{f}_{m}}= + \frac{R}{2}=+30 (converging mirror)
or \frac{1}{F}=\frac{2}{{60}}+\frac{1}{{30}}=\frac{2}{{30}}
The positive sign indicates that the resulting mirror is converging or concave.
Illustration
The plane surface of a plano-convex lens of focal length 60cm is silver plated. A point object is placed at a distance 20cm from the convex face of lens. Find the position and nature of the final image formed.
Solution
Using equation
\frac{1}{F}=\frac{2}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}
here, \displaystyle {{f}_{l}} = + 60 cm; \displaystyle {{f}_{m}} = \displaystyle \infty
or \frac{1}{F}=\frac{2}{{60}}+\frac{1}{\infty }=\frac{1}{{30}}
hence F = +30 cm
The problem is reduced to a simple case where a point object is placed in front of a concave (converging) mirror.
Using mirror formula
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}
here u = -20 cm; f = -30cm
hence \frac{1}{v}+\frac{1}{{-20}} = \frac{1}{{-30}}
thus v = 60 cm.
The image is erect and virtual.
Illustration
An equiconvex lens is placed on a plane mirror. An object coincides with its image when it is at a height of 24 cm from the lens. The gap between the lens and the mirror is filled with water ( \displaystyle {{\mu }_{w}} = 4/3). By how much distance should the object be now shifted so that it again coincides with its image? ( \displaystyle {{\mu }_{g}}= 1.5)
Solution
Let \displaystyle {{F}_{1}} be equivalent focal length of the lens-mirror combination
2 \displaystyle {{F}_{1}} = 24
\displaystyle {{F}_{1}} = 12 cm
\frac{1}{{{{F}_{1}}}}=\frac{2}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}=\frac{2}{{{{f}_{l}}}}+\frac{1}{\infty }
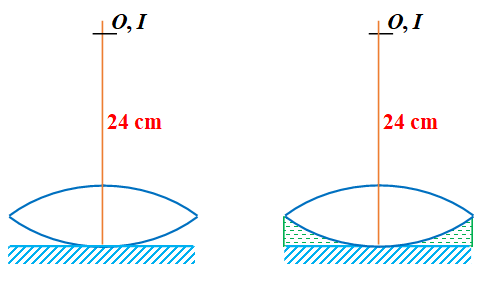
\displaystyle {{f}_{l}} = focal length of lens = 24 cm
When water is filled, we have a combination of glass-lens, water-lens and a plane mirror.
Let \displaystyle {{F}_{2}} be the equivalent focal length, then
\frac{1}{{{{F}_{2}}}}=\frac{2}{{{{f}_{l}}}}+\frac{2}{{{{f}_{w}}}}+\frac{1}{{{{f}_{m}}}}
=\frac{2}{{{{f}_{l}}}}+\frac{2}{{{{f}_{w}}}}+\frac{1}{\infty }
or
\frac{1}{{{{F}_{2}}}}=\frac{2}{{24}}+\frac{2}{{{{f}_{w}}}} —(1)
Applying lens maker’s formula
For glass lens:
\frac{1}{{24}}=\frac{1}{2}\times \left( {\frac{2}{R}} \right)
R =24 cm
For water lens
\frac{1}{{{{f}_{w}}}}=\left( {\frac{4}{3}-1} \right)\left( {\frac{1}{{-R}}-\frac{1}{\infty }} \right)
\frac{1}{{{{f}_{w}}}}=-\frac{1}{3}\times \left( {\frac{1}{R}} \right)
\displaystyle {{f}_{w}} = -72 cm
Substituting the value of \displaystyle {{f}_{w}} in equation (1)
\frac{1}{{{{F}_{2}}}}=\frac{2}{{24}}+\frac{2}{{-72}}
\displaystyle {{F}_{2}} = 18 cm
hence 2 \displaystyle {{F}_{2}} = 36 cm
Shift, s = (36 – 24) cm = 12 cm upwards
The object will coincide with the image at a height of 36 cm from the lens and hence it should be shifted 12 cm upwards.
Illustration
A glass convex lens has a focal length of 20 cm in air. What will be its focal length, when it is completely immersed in a liquid of refractive index 1.63? (Given \displaystyle {{\mu }_{g}} = 1.5)
Solution
\displaystyle \frac{1}{{{{f}_{a}}}}={{(}^{a}}{{\mu }_{g}}-1)\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
or
\displaystyle \frac{1}{{20}}=(1.5-1)\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
= \displaystyle 0.5\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
or \displaystyle \left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)=\frac{1}{{10}}
When lens is immersed in liquid,
\displaystyle \frac{1}{{{{f}_{l}}}}= \displaystyle \left( {\frac{{^{a}{{\mu }_{g}}}}{{^{a}{{\mu }_{l}}}}-1} \right)\,\,\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
= \displaystyle \left( {\frac{{1.5}}{{1.63}}-1} \right)\times \frac{1}{{10}}=-\frac{{0.13}}{{16.3}}
or \displaystyle {{f}_{l}}=-\frac{{16.3}}{{0.13}}=-125.4\text{cm}
Since focal length is negative, so convex lens will behave as concave or diverging lens in this liquid.
Illustration
A plano-convex lens has a thickness of 4 cm. When placed on a horizontal table with the curved surface in contact with it, the apparent depth of the bottom-most point of the lens is found to be 3 cm. If the lens is inverted such that the plane face is in contact with the table, the apparent depth of the centre of the plane face of the lens is found to be (25/8) cm. Find the focal length of the lens.
Solution
In case of refraction from a curved surface,
\displaystyle \frac{{{{\mu }_{2}}}}{v}-\frac{{{{\mu }_{1}}}}{u}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R}
So when curved surface is in contact with the table, refractive will take placed at plane surface.
So
\displaystyle \frac{1}{{-3}}-\frac{\mu }{{-4}}=\frac{{1-\mu }}{{-\infty }},
i.e., \displaystyle \mu =\frac{4}{3}
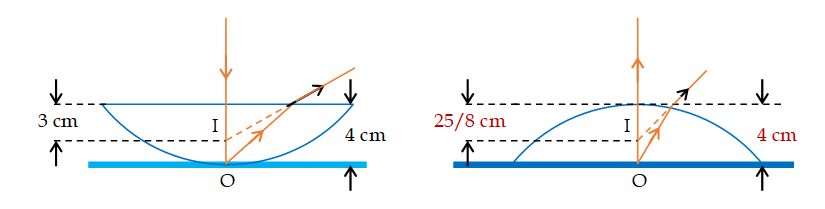
And when plane surface is on the table, refraction will take place at curved surface.
So
\displaystyle \frac{1}{{-(25/8)}}-\frac{{(4/3)}}{{(-4)}}=\frac{{1(-4/3)}}{{(-R)}}
i.e. \displaystyle -\frac{8}{{25}}+\frac{1}{3}=\frac{1}{{3R}}
or R = 25 cm
Now the lens is thick; as it has thickness 4 cm, there are two possibilities:
(a)
If the plane surface faces the incident parallel beam of light (figure A), refraction will take place only on the curved surface with
u = – \displaystyle \infty , v = f;
\displaystyle {{\mu }_{1}} = (4/3); \displaystyle {{\mu }_{2}} = 1
and R = –25 cm
So from
\displaystyle \frac{{{{\mu }_{2}}}}{v}-\frac{{{{\mu }_{1}}}}{u}=\frac{{{{\mu }_{2}}-{{\mu }_{1}}}}{R}
We have
\displaystyle \frac{1}{f}-\frac{{(4/3)}}{{-\infty }}=\frac{{1-(4/3)}}{{25}}
i.e. f = +75 cm. So the focal length i.e., distance of focus from plane surface = 4 + 75 = 79 cm.
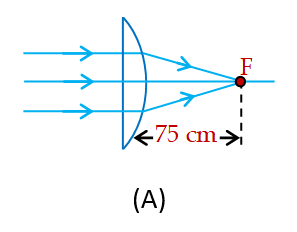
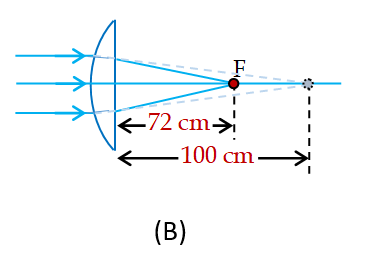
(b)
If the curved surfaces faces the incident parallel beam of light (figure B), from refraction at curved surface, we have
\displaystyle \frac{{(4/3)}}{{{{v}_{1}}}}-\frac{1}{\infty }=\frac{{(4/3)-1}}{{25}},
i.e. \displaystyle {{v}_{I}} = 100 cm
So the distance of I from plane surface will be 100 – 4 = 96 cm. The image I will act as virtual object for plane surface so that
\displaystyle \frac{1}{f}-\frac{{(4/3)}}{{96}}=\frac{{1-(4/3)}}{\infty },
i.e. f = 72 cm
i.e., in this situation focal length is 72 cm, i.e. focus will be at a distance of 72 cm from the plane surface.
Illustration
The convex surface of a plano convex lens is silvered whose radius of curvature is R. Find the focal length of the mirror thus formed.
Solution
\displaystyle {{P}_{{final}}}={{P}_{{lens}}}+{{P}_{{concave\text{ }mirror}}}+{{P}_{{lens}}}
As the ray of light first goes through lens then mirror then again lens.
\displaystyle {{P}_{{final}}}= \displaystyle \frac{1}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}+\frac{1}{{{{f}_{l}}}}
hence \displaystyle {{P}_{{final}}}=\frac{2}{{{{f}_{l}}}}+\frac{1}{{{{f}_{m}}}}
where \displaystyle {{f}_{l}} is given as
\displaystyle \frac{1}{{{{f}_{l}}}}=(n-1)\left( {\frac{1}{\infty }-\frac{1}{{-R}}} \right)
or \displaystyle \frac{1}{{{{f}_{l}}}}=+\frac{{(n-1)}}{R}
or \displaystyle {{f}_{m}}=-\frac{R}{2} ;
\displaystyle {{P}_{{final}}} = \displaystyle \frac{2}{{2R}}+\frac{2}{R}=\frac{3}{R}
\displaystyle {{f}_{{final}}} = \displaystyle -\frac{1}{{{{P}_{{\text{final}}}}}}=-\frac{R}{3}
and hence the final mirror will be concave.
Illustration
Two thin similar convex glass pieces are joined together front to front, with rear portion silvered and combination of glass pieces is placed at a distance a = 60 cm from a screen. A small object is placed on optical axis of the combination such that its m=2 times the magnified image formed on the screen.
If the air between the glass pieces is replaced by water ( \displaystyle \mu = 4/3), calculate the distance through which the object must be displaced so that a sharp image is again formed on the screen
Solution
Since the medium inside the glass pieces is air, its optical power will be zero. When its rear surface is polished it works as a concave mirror of focal length \displaystyle {{f}_{m}} = – r/2.
Since magnification m = 2
also distance of object from the mirror = \frac{a}{m} = 30 cm.
For the mirror
v = – a = -60 cm,
u = -30 cm,
f = \displaystyle {{f}_{m}}= -r/2.
Using mirror formula \frac{1}{v}+\frac{1}{u}=\frac{1}{f}
\displaystyle {{f}_{m}}= – 20 cm or r = 40 cm
When water is filled in space between glass pieces, an equi-convex lens of water is formed whose one surface is silvered.
Effective focal length of the combination
\frac{1}{F}=\frac{1}{{{{f}_{m}}}}+\frac{2}{{{{f}_{\ell }}}}
For equiconvex lens
\frac{1}{f}=(\mu -1)\left( {\frac{1}{{{{R}_{1}}}}-\frac{1}{{{{R}_{2}}}}} \right)
R1 = + r, R2 = -r, \displaystyle \mu = 4/3
f = \displaystyle {{f}_{l}}= 60 cm
Hence \frac{1}{F}=\frac{2}{{60}}+\frac{1}{{20}}=\frac{1}{{12}}
hence F = 12 cm.
Since, a sharp image is again formed on the screen, therefore, for this effective mirror
F = – 12 cm,
v = -a = -60 cm,
u = ?
\frac{1}{F}=\frac{1}{v}+\frac{1}{u}
which gives u = – 15 cm.
Hence the object must be moved through 30 – 15 = 15 cm towards the mirror.
Illustration
A thin equiconvex lens of glass of refractive index n = 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (n = 4/3).
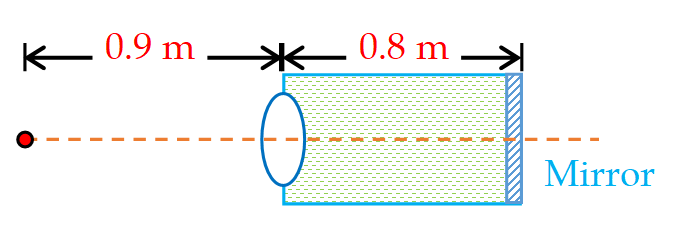
On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis, as shown in figure. The separation between the lens and the mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance of 0.9 m from the lens along its axis. Find the position (relative to the lens) of the image of the object formed by the system.
Solution
As one side of the lens is air and another is water. We should go as per the refraction at the curved surface formula. Focal length in air = 30 cm Þ \displaystyle \left| R \right| = 30 cm
For refraction from the first curved surface
\displaystyle \frac{{{{n}_{2}}}}{v}-\frac{{{{n}_{1}}}}{u}=\frac{{{{n}_{2}}-{{n}_{1}}}}{R}
\displaystyle \frac{{3/2}}{v}-\frac{1}{{-90}}=\frac{{(3/2)-1}}{{+30}}
or v = 270cm
This image will behave as an object for the second surface so
\displaystyle \frac{{2/3}}{{{v}’}}-\frac{{3/2}}{{+270}}=\frac{{4/3-3/2}}{{+30}}
hence \displaystyle {{v}^{\prime}}= + 120 cm
This will behave as a virtual object for the plane mirror and will form a real image in front of the mirror at a distance of 40 cm from the mirror. This image will behaves as an object for surface for of the lens.
\displaystyle \frac{{3/2}}{{{{v}’}’}}-\frac{{4/3}}{{-40}}=\frac{{3/2-4/3}}{{+30}}
or \displaystyle {{v}^{\prime}}= – 54 cm
This will again behaves as an object, for surface one of the lens
\displaystyle \frac{1}{{{{v}_{f}}}}-\frac{{3/2}}{{-54}}=\frac{{1-3/2}}{{-30}}
or \displaystyle {{v}_{f}}= – 90 cm
Final image will be 90 cm right of the lens.
Practice Questions (Basic Level)
Q.1
A thin convergent glass lens (mg = 1.5) has a power of +5.0 D. when this lens is immersed in a liquid of refractive index ml, it acts as a divergent lens of focal length 100 cm. The value of ml is
(a) 4/3 (b) 5/3 (c) 5/4 (d) 6/5
Ans. (b)
Q.2
Focal length of an equiconvex lens is 20 cm. If we cut it once perpendicular to principle axis, and then along principle axis. Then focal length of each part will be
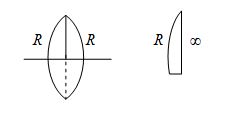
(a) 20 cm (b) 10 cm (c) 40 cm (d) 5 cm
Ans. (c)
Q.3
A liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangements, P and Q are shown. The system is
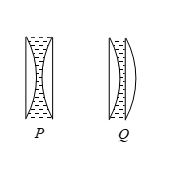
(a) divergent in P , convergent in Q
(b) convergent in P, divergent in Q
(c) convergent in both
(d) divergent in both
Ans. (c)
Practice Questions (JEE Main Level)
Q.1
A plastic hemisphere has a radius of curvature of 8 cm and an index of refraction of 1.6. On the axis halfway between the plane surface and the spherical one (4 cm from each) is a small object O. The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately
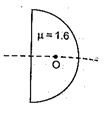
(a) 1.0 cm
(b) 1.5 cm
(c) 3.75 cm
(d) 2.5 cm
Ans (d)
Q.2
A beam of diameter ‘d’ is incident on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very large in comparison to d, then the diameter of the beam at the base of the hemisphere will be
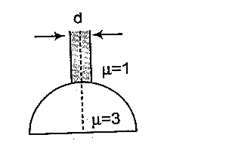
(a) \displaystyle \frac{3}{4}d
(b) d
(c) \displaystyle \frac{d}{3}
(d) \displaystyle \frac{2}{3}d
Ans (c)
Q.3
The image of point P when viewed from top of the slabs will be
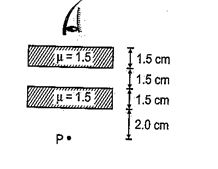
(a) 2.0 cm above P
(b) 1.5 cm above P
(c) 2.0 cm below P
(d) 1 cm above P
Ans (d)
Q.4
Two plano-convex lenses of glass of refractive index 1.5 have radii of curvature 20 cm and 30 cm respectively. They are placed in contact with the curved surfaces towards each other and the space between them is filled with water (m = 4/3). The focal length of the combination is
(a) -60 cm (b) 72 cm (c) 70 cm (d) 60.3 cm
Ans. (b)
Q.5
A thin convergent glass lens (mg = 1.5) has a power of +5.0 D. When this lens is immersed in a liquid of refractive index ml, it acts as a divergent lens of focal length 100 cm. The value of ml is
(a) 4/3 (b) 5/3 (c) 5/4 (d) 6/5
Ans. (b)
Q.6
Diameter of the flat surface of a circular plano-convex lens is 6 cm and thickness at the center is 3 mm. The radius of curvature of the curved part is
(a) 15 cm (b) 20 cm (c) 30 cm (d) 10 cm
Ans. (a)
Q.7
A sphere of radius R made of transparent material of refractive index m works like a thin lens having its optical center coinciding with the center of the sphere. The focal length of this thin lens is
(a) \frac{{\mu R}}{{\left( {\mu -1} \right)}}
(b) \frac{{\mu R}}{{2\left( {\mu -1} \right)}}
(c) \frac{{\mu R}}{{\left( {\mu +1} \right)}}
(d) \frac{{\left( {\mu -1} \right)R}}{{\left( {\mu +1} \right)}}
Ans. (b)
Q.8
Refraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance ( \displaystyle {{\mu }_{g}}=3/2). (Object is lying in the glass)
(a) should be greater than three times the radius of curvature of the refracting surface
(b) should be greater than two times the radius of curvature of the refracting surface
(c) should be greater than the radius of curvature of the refracting surface
(d) is independent of the radius of curvature of the refracting surface
Ans. (a)
Q.9
A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials of refractive indices \displaystyle {{\mu }_{1}} and \displaystyle {{\mu }_{2}} and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
(a) \displaystyle \frac{R}{{{{\mu }_{1}}-{{\mu }_{2}}}}
(b) \displaystyle \frac{{2R}}{{{{\mu }_{2}}-{{\mu }_{1}}}}
(c) \displaystyle \frac{R}{{2\left( {{{\mu }_{1}}-{{\mu }_{2}}} \right)}}
(d) \displaystyle \frac{R}{{2-\left( {{{\mu }_{1}}+{{\mu }_{2}}} \right)}}
Ans. (a)
Q.10
The x-z plane separates two media A and B of refractive indices \displaystyle {{\mu }_{1}}=1.5\,\,and \displaystyle {{\mu }_{2}}=2\,\,. A ray of light travels from A to B. Its directions in the two media are given by unit vectors \displaystyle {{\vec{u}}_{1}}\,=\,a\hat{i}\,+\,b\hat{j} and \displaystyle {{\vec{u}}_{2}}\,=\,c\hat{i}\,+\,d\hat{j}Then
(a) \displaystyle \frac{a}{c}=\frac{4}{3}
(b) \displaystyle \frac{a}{c}=\frac{3}{4}
(c) \displaystyle \frac{b}{d}=\frac{4}{3}
(d) \displaystyle \frac{b}{d}=\frac{3}{4}
Ans. (a)
Comprehension Based Question (11 and 12)
The curved surface of a thin plano-convex lens (n = 1.5) has a 12 cm radius of curvature. Locate the image of an object in air at infinity given that the surface that faces the object is
11.
curved
(a)24 cm
(b)30 cm
(c)20 cm
(d)35 cm
Ans (a)
12
flat.
(a)30 cm
(b)24 cm
(c)50 cm
(d)20 cm
Ans (b)
13.
A thin biconvex lens is made of glass (n = 1.5) with surface of radii of curvature 12 cm and 16 cm. An object is located 20cm from the lens. What are the position and linear magnification of the image?
(a)43.64 cm, 2.18
(b)43.50 cm, 2.00
(c)42.50 cm, 1.50
(d)50.00 cm, 2.00
Ans (d)
14.
A long cylindrical tube containing water is closed by an equiconvex lens of focal length 10 cm in air. A point source is placed along the axis of the tube outside it at a distance of 21 cm from the lens. Locate the final image of the source. Refractive index of the material of the lens = 1.5 and that of water = 1.33.
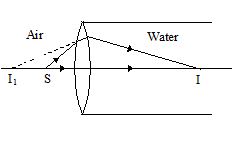
(a) 70 cm inside the tube
(b) 50 cm inside the tube
(c) 40 cm inside the tube
(d) 30 cm inside the tube
Ans (a)
Practice Questions (JEE Advance Level)
1.
A biconvex thin lens is prepared from glass(µ = 1.5), the two bounding surfaces having equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Where should an object be placed before this lens so that the image is formed on the object itself ?
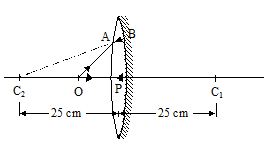
(a)12.0 cm
(b)12.5 cm
(c)13.0 cm
(d)13.5 cm
Ans (b)
2.
A glass ball of radius 10 cm has an index of refraction 1.5, the back half of the ball is silvered so that it acts as a concave mirror. Find the position of the final image seen by an eye (to the left of the object) for an object at 30 cm to the left of the front surface of the ball.
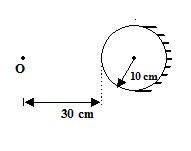
(a)20.0 cm
(b) 20.9 cm
(c)22.5 cm
(d)23.0 cm
Ans (b)
3.
In the figure, light is incident on the thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system.
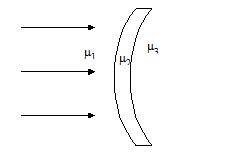
(a) f=\frac{{{{\mu }_{2}}R}}{{{{\mu }_{2}}-{{\mu }_{5}}}}
(b) f=\frac{{{{\mu }_{3}}R}}{{{{\mu }_{3}}-{{\mu }_{1}}}}
(c) f=\frac{{{{\mu }_{5}}R}}{{{{\mu }_{5}}-{{\mu }_{5}}}}
(d) f=\frac{{{{\mu }_{9}}R}}{{{{\mu }_{9}}-{{\mu }_{3}}}}
Ans (b)
Comprehension Based Question (4 and 5)
The convex surface of a thin concavo-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface
4.
where should a pin be placed on the optic axis such that its image is formed at the same place
(a)25 cm above the silvered lens.
(b)30 cm above the silvered lens
(c)15 cm above the silvered lens
(d)20 cm above the silvered lens
Ans (c)
5.
if the concave part is filled with water of refractive index (4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.
(a)3 cm towards the lens
(b)2 cm towards the lens
(c)1 cm towards the lens
(d)5 cm towards the lens
Ans(c)
Comprehension Based Question (6 and 7)
The figure shows a thin glass (µ =1.5) converging lens for which radii of curvature are R1 = 15 cm and R2 = 12 cm. To the left of lens is a square of area 100 cm2. The base of the square is on the principal axis, and the right side of the square is 20 cm from the lens.
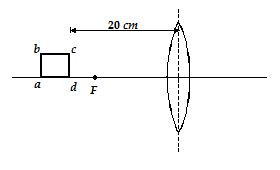
6.
Determine the focal length of the lens.
(a) 13.3 cm
(b) 13.8 cm
(c) 13.0 cm
(d) 12.8 cm
Ans (a)
7.
Determine the area of the image.
(a) 330 cm2
(b) 230 cm2
(c) 200 cm2
(d) 224 cm2
Ans (d)
Comprehension Based Question (8 and 9)
Two plano convex lenses L1 (m1 = 1.4) and L2 (m2 = 1.5) of same radii of curvature R = 20 cm are placed as shown in figure I.
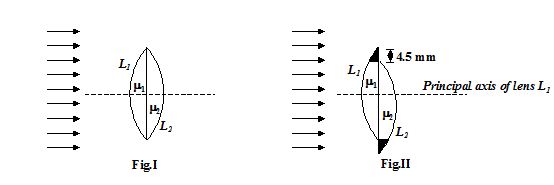
8.
Find the position of image of parallel beam of light relative to common principal axis.
(a)22.00 cm from the combination on the right side.
(b)23.55. cm from the combination on the right side.
(c)20.22 cm from the combination on the right side.
(d)22.22 cm from the combination on the right side.
Ans (d)
9.
Now the second lens is shifted vertically downward by a small distance 4.5 mm and the extended part of L1 and L2 are blackened as shown in figure II. Find new position of image of the parallel beam of light relative to principal axis of L1.
(a)22.00 cm behind the combination at a distance of 2.5 mm below the principal axis of L1.
(b)22.22 cm behind the combination at a distance of 2.5 mm below the principal axis of L1.
(c)22.55 cm behind the combination at a distance of 2.5 mm below the principal axis of L1.
(d)23.00 cm behind the combination at a distance of 2.5 mm below the principal axis of L1.
Ans (b)
Comprehension Based Question (10 and 11)
A thin equiconvex spherical glass lens (m= 3/2) of focal length 30 cm is placed on the x-axis with its optical center at x = 40 cm and principal axis coinciding with the x-axis. A light ray, given by the equation 39y = -X + 1 (x and y in cm) is incident on the lens, in the direction of positive x-axis.
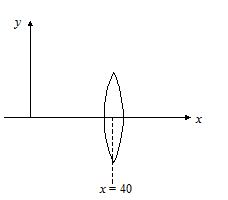
10.
Find the equation of refracted ray.
(a) y=\frac{2}{{110}}\left( {x-150} \right)
(b) y=\frac{1}{{140}}\left( {x-120} \right)
(c) y=\frac{1}{{120}}\left( {x-110} \right)
(d) y=\frac{1}{{130}}\left( {x-170} \right)
Ans (d)
11.
If the space on the right side of the lens
(x> 40 cm) is filled with a liquid of refractive index 4/3, find the new equation of refracted ray.
(a) -\frac{1}{{370}}\left( {x+330} \right)
(b) -\frac{1}{{250}}\left( {x+220} \right)
(c) -\frac{1}{{550}}\left( {x+330} \right)
(d) -\frac{1}{{350}}\left( {x+230} \right)
Ans (a)
Comprehension Based Question (12 and 13)
A cylindrical tube filled with water (mw = 4/3) is closed at its both ends by two silvered plano-convex lenses (see figure). Refractive index of lenses L1 and L2 are 2.0 and 1.5 while their radii of curvature are 5 cm and 9 cm respectively. A point object is placed somewhere at a point O on the axis of cylindrical tube. It is found that the object and the images coincide with each other. Then
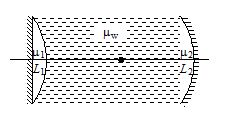
12.
calculate the length of the cylindrical tube,
(a)18 cm
(b) 20cm
(c) 25cm
(d) 30cm
Ans (a)
13.
find the position of object with respect to lens L1, and
(a)20 cm
(b)30 cm
(c)10 cm
(d)50 cm
Ans (c)


