Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Basic Level)
Q.1
What the equation of SHM with amplitude 8 cm and maximum particle speed 64p cm/s (where y is also in cm.)
(a) y = 64 sin 2 pt
(b) y = 8 sin 8 pt
(c) y = 64 sin 8 pt
(d) y = 8 sin 64 pt
Ans : (b)
Q.2
A particle moves such that its acceleration is given by a = -b2 What is the period of oscillation
(a) 2p/b (b) 2p/8b (c) b/2p (d) 2p/3b
Ans : (a)
Q.3
The displacement x (in centimeters) of an oscillating particle varies with time t (in seconds) as \displaystyle x=2\cos \left( {0.5\ \pi t+\frac{\pi }{3}} \right)The magnitude of the maximum acceleration of the particle in cms–2 is
(a) \displaystyle \frac{\pi }{2}
(b) \displaystyle \frac{\pi }{4}
(c) \displaystyle \frac{{{{\pi }^{2}}}}{2}
(d) \displaystyle \frac{{{{\pi }^{2}}}}{4}
Ans : (c)
Q.4
Two SHM’s are respectively represented by y = a sin(wt – kx) and y = b cos(wt – kx). Then the phase difference between the two is
(a) p/2 (b) p/4 (c) p/3 (d) None
Ans : (a)
Q.5
A particle executes SHM. Its velocities are v1 and v2 at displacement x1 and x2 from mean position respectively. The frequency of oscillation will be:
(a) \displaystyle 1000\sqrt{3}
(b) \displaystyle \frac{{2\sqrt{\beta }}}{{1+\beta }}
(c) \displaystyle \begin{array}{l}\frac{2}{{\left( {1+\beta } \right)}}+\\\end{array}
(d) \displaystyle \frac{{\sqrt{\beta }}}{{1+\beta }}
Ans. (b)
Q.6
Which of the following is a simple harmonic motion?
(a) Ball bouncing between two rigid vertical walls
(b) Particle moving in a circle with uniform speed
(c) Wave moving through a string fixed at both ends
(d) Earth spinning about its own axis
Ans. (c)
Q.7
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion?
(a) When v is maximum, a is maximum
(b) Value of a is zero, whatever may be the value of v
(c) When v is zero, a is zero
(d) When v is maximum, a is zero
Ans. (d)
Q.8
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4cm/s. The frequency of its oscillation is
(a) 3 Hz (b) 2 Hz (c) 4 Hz (d) 1 Hz
Ans. (d)
Q.9
The phase (at a time t) of a particle in simple harmonic motion tells:
(a) Only the position of the particle at time t
(b) One the direction of motion of the particle at time t
(c) Both the position and direction of motion of the particle at time t
(d) Neither the position of the particle nor its direction of motion at time t
Ans. (c)
Q.10
The displacement of a particle executing SHM is given by y = 0.25 sin 200 t cm. The maximum speed of the particle is
(a) 200 cm \displaystyle {{\in }_{0}}\,\,L\left( {\frac{{\Delta V}}{{\Delta t}}} \right),
(b) 100 cm \displaystyle \rho =KL+\frac{{MI}}{\omega },
(c) 50 cm \frac{{\Delta v}}{{\Delta z}}
(d) 5.25 cm \eta A\frac{{dv}}{{dz}},
Ans. (a)
Q.11
The displacement of a particle executing SHM is given by x = 0.01 sin 100 \displaystyle \eta (t + 0.05). The time period is
(a) 0.01 s (b) 0.02 s (c) 0.1 s (d) 0.2 s
Ans. (b)
Q.12
A body is vibrating in simple harmonic motion. If its acceleration is 12 cm/s2 at a displacement 3 cm from the mean position, then time period is
(a) 6.28 s (b) 3.14 s (c) 1.57 s (d) 2.57
Ans. (b)
Q.13
The average acceleration of a particle performing SHM over one complete oscillation is
(a) \frac{\pi }{2}
(b) {{\cos }^{{-1}}}(0.6)
(c) zero
(d) {{\tan }^{{-1}}}\left( {\frac{7}{5}} \right)
Ans. (c)
Practice Questions (JEE Main Level)
Q.1
A rough horizontal table moves horizontally in SHM, the period being 3 s and the maximum speed 4 m/s. A small heavy mass is placed on the table. Then the least coefficient of friction if the mass does not slide on the table throughout the motion.
(a) m = 0.85 (b) m = 0.65 (c) m = 0.55 (d) m = 0.25
Ans : (a)
Q.2
In how much time a particle will travel from its mean position to a displacement equal to half of its amplitude undergoing SHM with a time period of 2 seconds.
(a) 2/7s
(b) \displaystyle \frac{1}{6}s
(c) 1/2s
(d) 2/3s
Ans : (b)
Q.3
A person normally weighing 60 kg stands on a platform which oscillates up and down harmonically at a frequency 2.0 sec–1 and an amplitude 5.0 cm. If a machine on the platform gives the person’s weight against time, deduce the maximum and minimum reading it will show, take g = 10 m/sec2.
(a) Maximum reading = 20.3 kg, Minimum reading = 14.7 kg.
(b) Maximum reading = 107.3 kg, Minimum reading = 102.7 kg.
(c) Maximum reading = 107.3 kg, Minimum reading = 12.7 kg.
(d) None
Ans : (c)
Q.4
Two SHMs are given by y1 = a sin [(p/2)t + f] and \displaystyle \frac{3}{2}P The phase difference between these after 1 sec is:
(a) p (b) p/2 (c) p/4 (d) p/6
Ans. (d)
Q.5
A body of mass 5 g is executing SHM about a point O with amplitude 100 cm. If its max. velocity is 100 cm/sec, its velocity will be 50 cm/sec at a distance (in cm):
(a) 5
(b) \displaystyle \frac{{f\mu \prime \left( {\mu 1} \right)}}{{\left( {\mu \mu \prime } \right)}}
(c) \displaystyle \frac{{f\left( {\mu \prime \mu } \right)}}{{\mu \prime \left( {\mu 1} \right)}}
(d) \displaystyle \frac{{\mu \prime \left( {\mu 1} \right)}}{{f\left( {\mu \prime \mu } \right)}}
Ans. (c)
Q.6
A horizontal platform is made to execute SHM of amplitude a in the vertical direction. An object placed on the platform will lose contact with it, when the frequency of oscillation exceeds:
(a) \displaystyle {{\sin }^{{1}}}\left( {\frac{8}{9}} \right)
(b) \displaystyle {{I}_{0}}\cos \left( {\frac{x}{\beta }} \right)
(c) \displaystyle {{I}_{0}}{{\cos }^{2}}\left( {\frac{x}{\beta }} \right)
(d) \displaystyle {{I}_{0}}{{\cos }^{2}}\left( {\frac{{\pi x}}{\beta }} \right)
Ans. (b)
Q.7
A particle performs SHM along a straight line with the period T and amplitude A. The mean velocity of the particle averaged over the time interval during which it travels a distance A/2 starting from the extreme position is:
(a) \displaystyle \left( {\frac{{{{I}_{0}}}}{4}} \right){{\cos }^{2}}\left( {\frac{{\pi x}}{\beta }} \right)
(b) \displaystyle \frac{\lambda }{{4(\mu -1)}}
(c) \displaystyle \frac{\lambda }{{2(\mu -1)}}
(d) \displaystyle \frac{\lambda }{{\mu -1}}
Ans. (d)
Q.8
The time period and the amplitude pendulum are 4 second and 0.20 metre respectively. If the displacement is 0.1 m at time t = 0, the equation of its displacement is represented by:
(a) y = 0.2 sin (0.5pt)
(b) y = 0.2 sin (0.5pt)
(c) y = 0.1 sin (pt + p/6)
(d) y = 0.1 sin (0.5pt)
Ans. (b)
Q.9
The function sin2 (wt) represents:
(a) A periodic, but not simple harmonic motion with a period \displaystyle \sqrt{{\frac{{3\lambda D}}{2}}}
(b) A periodic, but not simple harmonic motion with a period \displaystyle \sqrt{{\lambda D}}
(c) A simple harmonic motion with a period \displaystyle \sqrt{{\frac{{\lambda D}}{2}}}
(d) A simple harmonic motion with a period \displaystyle \sqrt{{3\lambda D}}
Ans. (b)
Q.10
A particle executes linear simple harmonic motion with an amplitude of 2 cm. When the particle is at 1 cm from the mean position the magnitude of its velocity is equal to that of its acceleration. Then its time period in second is:
(a) \displaystyle {{\cos }^{{1}}}\sqrt{{\frac{{12}}{{50}}}}
(b) \displaystyle \frac{1}{{\sqrt{2}}}m/{{s}^{2}}\,\,towards\,\,northeast
(c) \displaystyle \frac{1}{{\sqrt{2}}}m/{{s}^{2}}\,\,towards\,\,northwest
(d) \displaystyle 1\text{/}2\,\,m/{{s}^{2}}\,\,towards\,\,northwest
Ans. (c)
Q.11
The speed (v) of a particle moving along a straight line, when it is at a distance (x) from a fixed point on the line, is given v2 = 144 – 9x2. Select wrong alternate:
(a) Displacement of the particle £ distance moved by it
(b) The magnitude of acceleration at a distance 3 units from the fixed point is 27 units
(c) The motion is simple harmonic with \displaystyle \frac{{{{E}^{2}}}}{{{{\mu }_{0}}}} units
(d) The maximum displacement from the fixed point is 4 units
Ans. (c)
Q.12
A body executes SHM whose period is 16 s. Two seconds after it passes the equilibrium position, its velocity is 1 ms-1. The amplitude of SHM is:
(a) 6.3 m (b) 1.8 m (c) 3.6 m (d) 2.4 m
Ans. (c)
Q.13
For a particle in SHM, if the amplitude of the displacement is a and the amplitude of velocity is v, the amplitude of acceleration is
(a) va
(b) \frac{\pi }{4}
(c) \overset{\to }{\mathop{A}}\,\,\,and\,\,\overset{\to }{\mathop{B}}\,
(d) \overset{\to }{\mathop{A}}\,\cdot (\overset{\to }{\mathop{B}}\,\times \overset{\to }{\mathop{A}}\,)
Ans. (d)
Q.14
Out of the following functions representing motion of a particle which represents SHM
- \overset{\to }{\mathop{A}}\,
- \overset{\to }{\mathop{B}}\,
- |\overset{\to }{\mathop{A}}\,+\overset{\to }{\mathop{B}}\,|=|\overset{\to }{\mathop{A}}\,-\overset{\to }{\mathop{B}}\,|
- \overset{\to }{\mathop{A}}\,=3\hat{i}+4\hat{j}+5\hat{k}
(a) only IV does not represent SHM
(b) I and III
(c) I and II
(d) only I
Ans. (b)
Q.15
The displacement time graph of a particle executing SHM is shown in figure. Which of the following statement is false?
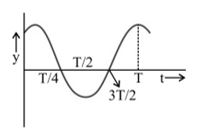
(a) The acceleration is maximum at t = T
(b) The force is zero at \displaystyle \frac{\pi }{{30\sqrt{2}}}cm/sa
(c) The potential energy equals the total oscillation energy \displaystyle \vec{P},\,\,\vec{Q},\,\,and\,\,R
(d) None of the above
Ans. (d)
Practice Questions (JEE Advance Level)
1.
A body oscillates with SHM, according to the equation
x=\left( {5.0} \right)m cos [(2p rad/s) t + p/4]
At t = 1.5 s, calculate
(a)
Displacement
(a)-2.765 m
(b)2.765 m
(c)3.535 m
(d)-3.535 m
Ans (d)
(b)
speed
(a) 2.48 m/s
(b)18.58 m/s
(c)20.67 m/s
(d)22.22 m/s
Ans (d)
(c)
acceleration of the body.
(a)130.35 m/s2
(b)132.62 m/s2
(c)139.56 m/s2
(d)150.45 m/s2
Ans (c)
2.
The displacement from equilibrium of a particle is given by x = Acos(w t – p/3). Which, if any, of the following are equivalent expressions
(a) x = Acos(w t + p/3)
(b) x = Asin(wt + p/6)
(c) x = A cos(wt + 5p/3)
(d) x = A sin(wt – 5p/6)
Ans (b) and (c)
3.
Which of the following functions are
(a) aperiodic (b) periodic but not simple harmonic (c) simple harmonic
(i) sin 2wt (ii) 1 + cos 2wt (iii) a sin wt + b cos wt (iv) sin wt + sin 2wt + cos 3wt
(v) sin3wt (vi) log (1 + wt) (vii) exp (-wt)
Ans (a) Functions (vi), (vii) are a periodic.
(b) Functions (ii), (iv) and (v) are periodic but not simple harmonic.
(c) Functions (i) and (iii) are simple harmonic.
4.
The condition |v| = 0.5 vmax, where vmaxis the maximum speed, occurs four times in each cycle in the oscillation of a block-spring system. Determine the first four time (>0) given that the displacement from equilibrium is x = 0.35 cos(3.6t – 0.5) m.
(a)0.284 s, 0.866 s, 1.16 s, 0.4 s
(b)0.284 s, 0.866 s, 1.16 s, 8.32 s
(c)0.284 s, 0.866 s, 2.3 s, 0.3 s
(d)0.284 s, 0.866 s, 1.16 s, 1.74 s
Ans (d)
5.
A particle of mass m is moving in a force field whose potential energy is given by u = a + bx2 J/kg. Show that the motion of particle is simple harmonic. Find the frequency in Hz.
(a) \displaystyle \left( {\frac{3}{\pi }\,\,\sqrt{{\frac{a}{5}}}} \right)
(b) \displaystyle \left( {\frac{1}{\pi }\,\,\sqrt{{\frac{a}{2}}}} \right)
(c) \displaystyle \left( {\frac{1}{\pi }\,\,\sqrt{{\frac{a}{3}}}} \right)
(d) \displaystyle \left( {\frac{1}{\pi }\,\,\sqrt{{\frac{a}{2}}}} \right)
Ans (d)
6.
The average speed over the period of a complete oscillation of a particle performing rectilinear SHM is 2 cm/s. If the particle attains this speed when it is at a point P whose distance from the centre O is 4 cm, determine the amplitude
(a)1.125 cm
(b)2.154 cm
(c)0.56 cm
(d)1.075 cm
Ans (a)
7.
A particle in SHM is described by the displacement function
x=A\cos \left( {\omega t+\varphi } \right), w = 2p/T
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is p cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is p s-1.
(a)2p/4
(b)p/4
(c)3p/4
(d)8p/5
Ans (c)
8.
A spring balance has a scale that reads 50 kg. The length of the scale is 20 cm. A body suspended from this spring, when displaced and released, oscillates with period of 0.60 s. What is the weight of the body?
(a)219.1 N = 21.04 kgf
(b)219.1 N = 20.03 kgf
(c)219.1 N = 22.36 kgf
(d)219.1 N = 25.55 kgf
Ans (c)
