Video Lectures
Theory For Notes Making
Periodic Motion:
Any motion, which repeats itself after regular interval of time from the same initial position is called periodic motion
Example:
(i) Motion of the hands of a clock
(ii) Motion of the earth around the sun
(iii) Motion of the piston in a cylinder
(iv) Motion of the ball in a bowl
(v) Motion of the liquid in a U-tube.
Oscillatory/Vibratory Motion:
If in the case of periodic motion, the particle moves back and fourth (or to and fro) about at an equilibrium point. Then, the motion is said to be oscillatory.
Example:
(i) Motion of the balance wheel of a watch.
(ii) Motion of the needle of a serving machine.
(iii) Motion of the molecules in a solid around fixed littice sites.
(iv) Vibrations of the prongs of a tuning fork.
S.H.M:
If in the case of oscillatory motion a particle moves back and forth (or up and down) about a fixed point (called equilibrium position) via, a force or torque (called restoring force or torque), which is directly proportional to the displacement and opposite in direction to the displacement from equilibrium is called simple harmonic.
Example:
(i) Conical pendulum
(ii) Spring pendulum
(iii)Simple pendulum
(iv) Physical pendulum
(v) Torsional pendulum
Consider a reference particle, moving on a circle of reference of radius , with uniform angular velocity \omega . Let the particle start from the point X and trace an angle \theta \theta radian in time as it reaches the point P. Therefore, \displaystyle \omega =\theta /tor \theta =\omega t, Let the projection of the particle P on diameter \mathbf{YOY’} be at M. Then \mathbf{OM}=\mathbf{y}, is the displacement in S.H.M at time .
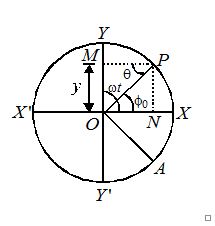
In \Delta OPM,\,\,\,\sin \theta =\frac{{OM}}{{OP}}=\frac{y}{a}
or y=a\sin \theta =a\sin \omega t …(i)
Important Notes:
(a) If projection of P is taken on diameter XOX’, then point N will be executing S.H.M. Here, ON=x=displacement in S.H.M at time
In \Delta ONP,\,\,\,\cos \theta =\frac{{ON}}{{OP}}=\frac{x}{a}
or x=a\cos \theta =a\cos \omega t …(ii)
(b) If A is the starting position of the particle of reference such that \angle AOX={{\varphi }_{o}} and \angle AOP=\omega t.
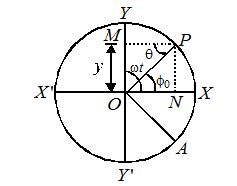
\theta =\angle XOP=\omega t-{{\varphi }_{o}}
From (i) , y=a\sin (\omega t-{{\varphi }_{o}})
(ii), x=a\cos (\omega t-{{\varphi }_{o}})
Here -{{\varphi }_{o}} is called the initial phase of epoch of S.H.M.
If B is the starting position of the particle of reference such that \angle BOX={{\varphi }_{o}} and \angle BOP=\omega t, then
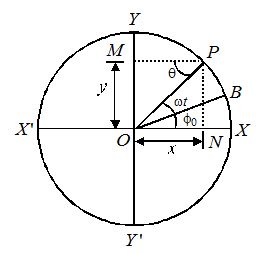
\theta =\angle XOP=\omega t+{{\varphi }_{o}}
From (i), y=a\sin (\omega t+{{\varphi }_{o}})
(ii), x=a\cos (\omega t+{{\varphi }_{o}})
Here, +{{\varphi }_{o}} is called initial phase or epoch of SHM.
Parameters Of SHM
For a body executing SHM along x axis the equation of displacement is given by
x=a\sin (\omega t+\varphi )
The SHM can be defined in terms of following parameters or quantities.
(1)
Amplitude (a): It is defined as the maximum (positive or negative) value of displacement from equilibrium position. Since maximum and minimum values of sine function are +1 and –1, therefore it’s amplitude are + a and-a. Further, span of S.H.M is S=2a.
(2)
Time period (T): The smallest time interval after which the oscillation repeat itself is called its time period (T)\,,\,\,\,\,T=\frac{{2\pi }}{\omega }.
(3)
Frequency (f): The reciprocal of time period is defined as frequency, f=\frac{1}{T}=\frac{\omega }{{2\pi }} whereis ω angular frequency.
(4)
Phase: The term (\omega t+\varphi ) is term defined as phase of the oscillation.
(5)
Phase constant (\varphi ):
The constant (\varphi ) in the equation of SHM is called epoch or initial phase.
Equation Of Velocity and Acceleration for a body in SHM
One very important distinctive feature of SHM is the relation between the displacement, velocity and acceleration of oscillatory particle.
x = asin ωt
v = \frac{{dx}}{{dt}} = ωacos ωt = ωa sin (ωt + \frac{\pi }{2})
acceleration ac = \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}= – ω2a sin ωt = ω2a sin (ωt + p)
Notice that the maximum displacement is a, the maximum speed is ωa, and the maximum acceleration is ω2a.
The displacement, velocity and acceleration versus time graphs have been plotted in figure given below
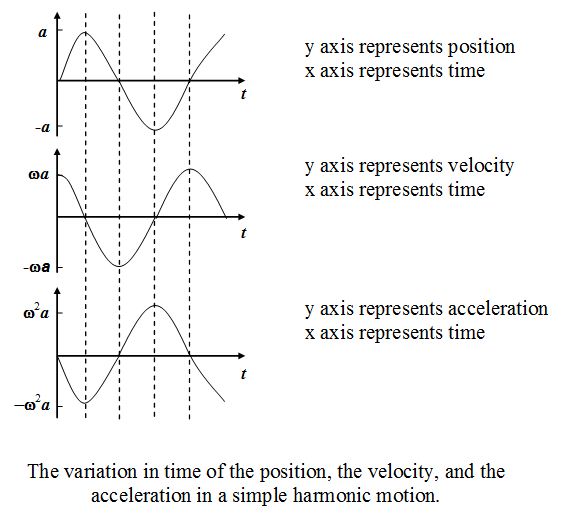
The velocity function is π/2 ahead of the displacement function and the acceleration function is π/2 ahead of the velocity function.
Relation Between Velocity and Displacement
We know that
x = a sin ωt
hence \displaystyle \sin \omega t=\frac{x}{a} (1)
also v= \frac{{dx}}{{dt}} = ωa cos ωt(2)
but \displaystyle \cos \omega t=\sqrt{{1-{{{\sin }}^{2}}\omega t}}=\sqrt{{1-\frac{{{{x}^{2}}}}{{{{a}^{2}}}}}} (Using equation (1)
On putting the above value of cos ωt in equation (2) we get the equation of velocity
\displaystyle v=\omega a\sqrt{{1-\frac{{{{x}^{2}}}}{{{{a}^{2}}}}}}
hence finally we get \displaystyle v=\omega \sqrt{{{{a}^{2}}-{{x}^{2}}}}.
To get the equation of acceleration just differentiate equation (2) with respect to time and substitute the value of sin ωt from equation (1) .
we know v = ωa cos ωt from equation no.(2)
on differentiating we get acceleration ac = \frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}= – ω2a sin wt
hence \displaystyle {{a}_{c}}=-{{\omega }^{2}}a.\frac{x}{a}
and finally we get ac = – ω2x
Remember :
S. No | Physical Quantity | At Equilibrium Position | At Extreme Position |
1. | Displacement x =a\sin \,\omega t | Minimum =0 | Maximum=a |
2. | Velocity =\omega \sqrt{{{{a}^{2}}-{{x}^{2}}}} | Maximum=ωa | Minimum=0 |
3. | Acceleration |a|={{\omega }^{2}}x | Minimum=0 | Maximum ={{\omega }^{2}}a |
Illustration
A particle executes simple harmonic motion of amplitude a and time period T. What is time (t) taken by it to move from mean position to half of amplitude.
Solution
\displaystyle y=a\sin \omega t
\displaystyle \frac{a}{2}=a\sin \omega t
\displaystyle \Rightarrow \omega t=\frac{\pi }{6}
\displaystyle \frac{{2\pi }}{T}t=\frac{\pi }{6}
\displaystyle t=\frac{T}{{12}}
Note: If particle is going from extreme to mean position.
\displaystyle y=a\cos \omega t or \displaystyle \omega t=\frac{\pi }{3}
\displaystyle \frac{a}{2}=a\cos \omega t or \displaystyle t=T/6\sec
Illustration
A body of mass 1 kg is executing simple harmonic motion which is given by x = 6.0 cos (100 t + π/4)cm. What is the (i) amplitude of displacement, (ii) frequency, (iii) initial phase, (iv) velocity, (v) acceleration, (vi) maximum kinetic energy?
Solution
The given equation of SHM is x = 6.0 cos (100 t + π/4) cm.
Comparing it with the standard equation of SHM, x = a cos (wt + ∅), we have
(i) amplitude a = 6.0 cm
(ii) frequency w = 100/sec.
(iii) initial phase f =π/4
(iv) velocity \displaystyle v=\omega \sqrt{{({{a}^{2}}-{{x}^{2}})}}=100\ \sqrt{{(36-{{x}^{2}})}}
(v) acceleration \displaystyle =-{{\omega }^{2}}x=-{{(100)}^{2}}x=-{{10}^{4}}x
(vi) kinetic energy \displaystyle =\frac{1}{2}m{{v}^{2}}=\frac{1}{2}m{{\omega }^{2}}({{a}^{2}}-{{x}^{2}})
When x = 0, the kinetic energy is maximum, i.e.,
(K.E.)max = \displaystyle \frac{1}{2}m{{\omega }^{2}}{{a}^{2}}
\displaystyle =\frac{1}{2}\times 1\times {{10}^{4}}\times {{\left( {\frac{6}{{100}}\ } \right)}^{\text{2}}}\text{metre}
= 18 joules.
Illustration
Two particles execute SHM of same amplitude and frequency along the same straight line. They pass one another, when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
Solution
\displaystyle {{y}_{1}}= A sin wt and \displaystyle {{y}_{2}}= Asin (wt + f)
wheny = A/2, \displaystyle \sin \omega t=\frac{1}{2}
\displaystyle \text{And}\ A/2=A\sin \ (\omega t+\phi )
sin wt cos Φ + cos wt sin Φ \displaystyle =\frac{1}{2}.
Substituting the value of sin wt and cos wt, we get
cosΦ – 1 = \displaystyle \sqrt{3} sin Φ
or (cos Φ – 1)2 = 3 (1 – cos2 Φ)
Solving we get, \displaystyle \cos \phi =+1\ \text{or}\ -\frac{1}{2}.
When cos Φ = + 1, Φ = 0 (not acceptable).
\displaystyle \cos \phi =-\frac{1}{2},\ \phi =120{}^\circ .
Objective Assignment
Q.1
What the equation of SHM with amplitude 8 cm and maximum particle speed 64p cm/s (where y is also in cm.)
(a) y = 64 sin 2 pt
(b) y = 8 sin 8 pt
(c) y = 64 sin 8 pt
(d) y = 8 sin 64 pt
Ans : (b)
Q.2
A particle moves such that its acceleration is given by a = -b2 What is the period of oscillation
(a) 2p/b (b) 2p/8b (c) b/2p (d) 2p/3b
Ans : (a)
Q.3
The displacement x (in centimeters) of an oscillating particle varies with time t (in seconds) as \displaystyle x=2\cos \left( {0.5\ \pi t+\frac{\pi }{3}} \right)The magnitude of the maximum acceleration of the particle in cms–2 is
(a) \displaystyle \frac{\pi }{2}
(b) \displaystyle \frac{\pi }{4}
(c) \displaystyle \frac{{{{\pi }^{2}}}}{2}
(d) \displaystyle \frac{{{{\pi }^{2}}}}{4}
Ans : (c)
Q.4
Two SHM’s are respectively represented by y = a sin(wt – kx) and y = b cos(wt – kx). Then the phase difference between the two is
(a) p/2 (b) p/4 (c) p/3 (d) None
Ans : (a)
Q.5
A particle executes SHM. Its velocities are v1 and v2 at displacement x1 and x2 from mean position respectively. The frequency of oscillation will be:
(a) \displaystyle 1000\sqrt{3}
(b) \displaystyle \frac{{2\sqrt{\beta }}}{{1+\beta }}
(c) \displaystyle \begin{array}{l}\frac{2}{{\left( {1+\beta } \right)}}+\\\end{array}
(d) \displaystyle \frac{{\sqrt{\beta }}}{{1+\beta }}
Ans. (b)
Q.6
Which of the following is a simple harmonic motion?
(a) Ball bouncing between two rigid vertical walls
(b) Particle moving in a circle with uniform speed
(c) Wave moving through a string fixed at both ends
(d) Earth spinning about its own axis
Ans. (c)
Q.7
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion?
(a) When v is maximum, a is maximum
(b) Value of a is zero, whatever may be the value of v
(c) When v is zero, a is zero
(d) When v is maximum, a is zero
Ans. (d)
Q.8
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4cm/s. The frequency of its oscillation is
(a) 3 Hz (b) 2 Hz (c) 4 Hz (d) 1 Hz
Ans. (d)
Q.9
The phase (at a time t) of a particle in simple harmonic motion tells:
(a) Only the position of the particle at time t
(b) One the direction of motion of the particle at time t
(c) Both the position and direction of motion of the particle at time t
(d) Neither the position of the particle nor its direction of motion at time t
Ans. (c)
Q.10
The displacement of a particle executing SHM is given by y = 0.25 sin 200 t cm. The maximum speed of the particle is
(a) 200 cm \displaystyle {{\in }_{0}}\,\,L\left( {\frac{{\Delta V}}{{\Delta t}}} \right),
(b) 100 cm \displaystyle \rho =KL+\frac{{MI}}{\omega },
(c) 50 cm \frac{{\Delta v}}{{\Delta z}}
(d) 5.25 cm \eta A\frac{{dv}}{{dz}},
Ans. (a)
Q.11
The displacement of a particle executing SHM is given by x = 0.01 sin 100 \displaystyle \eta (t + 0.05). The time period is
(a) 0.01 s (b) 0.02 s (c) 0.1 s (d) 0.2 s
Ans. (b)
Q.12
A body is vibrating in simple harmonic motion. If its acceleration is 12 cm/s2 at a displacement 3 cm from the mean position, then time period is
(a) 6.28 s (b) 3.14 s (c) 1.57 s (d) 2.57
Ans. (b)
Q.13
The average acceleration of a particle performing SHM over one complete oscillation is
(a) \frac{\pi }{2}
(b) {{\cos }^{{-1}}}(0.6)
(c) zero
(d) {{\tan }^{{-1}}}\left( {\frac{7}{5}} \right)
Ans. (c)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.


