Video Lectures
Theory For Making Notes
Circular Motion:
If a particle is moving in a plane in such a way that, its distance from a fixed point is a constant then path followed by it is a circle. Such motion is known as circular motion.
Angular Position :
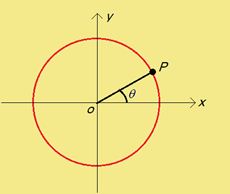
Angle between the reference axis and the position vector of a particle is the Angular position
Angular Velocity :
As the particle moves on the circle its angular position θ changes. Suppose the particle goes to a near by point in time ∆t so that θ increases to θ+∆θ.
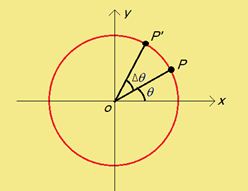
The rate of change of angular position is called angular velocity. Thus the angular velocity is given by :
Instantaneous angular velocity \omega =\underset{{\Delta t\to 0}}{\mathop{{\lim }}}\,\frac{{\Delta \theta }}{{\Delta t}}=\frac{{d\theta }}{{dt}}
If a body completes a full circle in time period ‘T’
then \displaystyle \omega \,=\,\frac{{2\pi }}{T}\,=\,2\pi \upsilon , = frequency of revolution in rps.
Angular Velocity Vector :
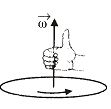
Angular speed \displaystyle \omega is the magnitude of vector called the angular velocity \displaystyle \vec{\omega } of the particle. Direction of \displaystyle \vec{\omega } can be determined from circular motion right hand rule. Curl your fingers of right hand in the sense of rotation of particle, then the extended thumb points in the direction of \displaystyle \vec{\omega }.
Uniform Circular Motion
If a particle moves along the circumference of a circle with constant speed, the motion is termed as uniform circular motion.
Here, the magnitude of the velocity vector remains constant but the direction changes continuously and therefore it is an accelerated motion. To analyze the circular motion, we choose a reference frame in the form of a xy–plane with its origin at the centre of the circle on which the particle moves.
Let R be the radius of the circle. The instantaneous position of the particle is expressed by an angle q between a radial line OP and a reference line such as OA.
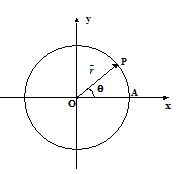
Suppose the particle starts at t = 0 from point A and reaches point P in time t. The position vector of the particle rotates by an angle q. If the distance moved along the circumference of the circle is s then
s = R θ
Differentiating with respect to time, we get
\frac{{ds}}{{dt}}=R\frac{{d\theta }}{{dt}}
The quantity \frac{{ds}}{{dt}} = v the speed of the particle at any instant.
The quantity \frac{{d\theta }}{{dt}} is called the angular speed of the particle and it is denoted by w (omega).
Thus v = Rw
Note : In vector form \displaystyle \vec{v}\,\,=\,\,\vec{\omega }\,\,\times \,\,\vec{r}
We can now write the position vector of the particle \displaystyle \vec{r}. From the figure,
\displaystyle \vec{r} = R cos q \hat{i} + R sin q \hat{j}
Differentiating with respect to time, we get
\vec{v}=\frac{{d\vec{r}}}{{dt}}=-R\sin \theta .\frac{{d\theta }}{{dt}}\hat{i}+R\cos \theta \frac{{d\theta }}{{dt}}\hat{j}
= –Rw sin q \hat{i} + Rw cos q \hat{j}
The magnitude of \left| {\vec{v}} \right|=\sqrt{{{{{\left( {-R\omega \sin \theta } \right)}}^{2}}+{{{\left( {R\omega \cos \theta } \right)}}^{2}}}} = Rw as expected.
If we take the dot product of \displaystyle \vec{v} and \displaystyle \vec{r}, it is observed to be zero. Thus the velocity vector is perpendicular to the position (radius) vector i.e. it is along the tangent to the circle. This is once again an expected result.
Next, we differentiate with respect to time to get , thus
\vec{a}=\frac{{d\vec{v}}}{{dt}}=-R\omega \cos \theta \frac{{d\theta }}{{dt}}\hat{i}-R\omega \sin \theta \frac{{d\theta }}{{dt}}\hat{j}
= -w2 \left( {R\cos \theta \,\,\hat{i}+R\sin \theta \,\,\hat{j}} \right) (Q w = \frac{{d\theta }}{{dt}})
\vec{a}=-{{\omega }^{2}}\vec{r}
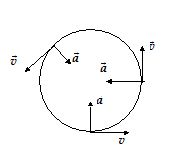
The acceleration vector has a magnitude ω2R and is oppositely directed to \displaystyle \vec{r} i.e. towards the centre of circle. This acceleration is called the centripetal acceleration. We now summarize the situation in the figure.
Note that the magnitude of centripetal acceleration can also be written as \frac{{{{v}^{2}}}}{R}
Non-Uniform Circular Motion
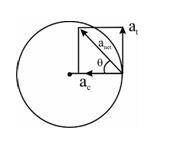
We now consider the more general case of circular motion in which the speed of the particle is not constant. In uniform circular motion, the acceleration resulted from the change in direction only of the velocity vector. Here, both the magnitude and direction of the velocity vector change and, therefore, not only the centripetal acceleration, we have another acceleration also which results from the change in magnitude of the velocity vector. This acceleration, is called the tangential acceleration, it has a magnitude equal to \frac{{dv}}{{dt}} and is directed either in the direction of \vec{v} (speed increasing) or opposite to the direction of \vec{v} (speed decreasing). Note that in this case, the magnitude of centripetal acceleration is also not a constant as it depends on v. Thus, in case of non-uniform circular motion, the total acceleration vector has two components
(i) Centripetal acceleration ac= \frac{{{{v}^{2}}}}{R} = w2R
(ii) Tangential acceleration at= \frac{{dv}}{{dt}}
Hence anet = \sqrt{{a_{c}^{2}+a_{t}^{2}}}
also tanθ =\frac{{{{a}_{t}}}}{{{{a}_{c}}}} where θ is the angle made by the net acceleration with the radius
In non uniform circular motion when the angular velocity of a body changes with time, another acceleration called angular acceleration is also considered. It can be defined as the time rate of change of angular velocity and is denoted by α.
Concept : 1.
The angular acceleration vector \displaystyle \vec{\alpha } (t) points in the direction of the change in the angular velocity vector \displaystyle \vec{\omega }\left( t \right). If speed of particle increases or decreases, the angular velocity vector also increases or decreases. Direction of angular velocity vector is always normal to plane rotation.
Therefore the angular acceleration vector \displaystyle \vec{\alpha }\left( t \right) is directed either parallel to \displaystyle \vec{\omega }\left( t \right) when the particle is speeding up along the circle, or antiparallel to \displaystyle \vec{\omega }\left( t \right) when the particle is slowing.
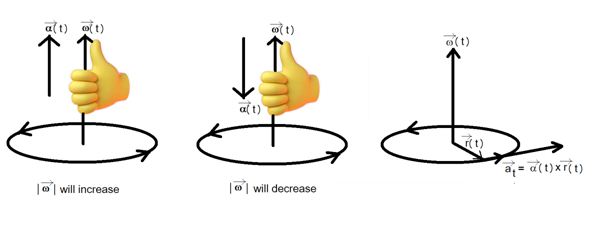
Hence \alpha =\frac{{d\omega }}{{dt}}, And at = r.α
If α is constant then
\begin{array}{l}\omega =\omega o+\alpha t,\\\theta =\omega ot+\frac{1}{2}\alpha {{t}^{2}},\\{{\omega }^{2}}=\omega {{o}^{2}}+2\alpha \theta .\end{array} \displaystyle \}These equations are called the equations of kinematics in circular motion.
\displaystyle \omega = final angular velocity.
\displaystyle {{\omega }_{0}}= Initial angular velocity
\displaystyle \theta = angular displacement
Tangential and Normal acceleration
When a particle moves along in a curvilinear path with variable speed (like non-uniform circular motion) it can be shown to have two acceleration components.
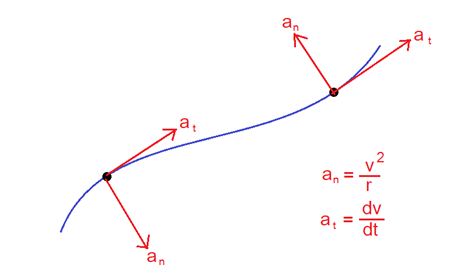
One of these components is called the tangential component at resulting from a change in magnitude of velocity vector and has a magnitude at= \frac{{dv}}{{dt}}. The second component is termed as the normal component anand its magnitude is equal to \displaystyle \frac{{{{v}^{2}}}}{r} where r is the radius of curvature of the path at that point.
Practice Questions (Level-1)
1.
A particle is moving along a circular path with uniform speed. Through what angle does its angular velocity change when it completes half of the circular path?
(a) 360° (b) 180° (c) 45° (d) 0°
Ans (d)
2.
To enable a particle describe a circular path, what should be the angle between its velocity and acceleration?
(a) 180° (b) 90°
(c) 45° (d) 0°
Ans (b)
3.
The angular speed of the second’s hand of a clock is
(a) \frac{\mathbf{1}}{{\mathbf{60}}}\mathbf{rad/s} (b) \frac{\mathbf{\pi }}{{\mathbf{60}}}\mathbf{rad/s} (c) \frac{{\mathbf{2\pi }}}{{\mathbf{60}}}\mathbf{rad/s} (d) \frac{{\mathbf{360}}}{{\mathbf{60}}}\mathbf{rad/s}
Ans .(c)
4.
A particle is moving along a circular path. The angular velocity, linear velocity, angular acceleration and centripetal acceleration of the particle at any instant respectively are and . Which of the following relations is not correct?
(a) \vec{\omega }\bot \vec{v} (b) \vec{\omega }\bot \vec{\alpha } (c) \vec{\omega }\bot {{\vec{a}}_{c}} (d) \vec{v}\bot {{\vec{a}}_{c}}
Ans (b)
5.
The length of second’s hand in a watch is 1 cm. The change in velocity of its tip in a period of 15s is
(a) Zero (b) \left( {\frac{\pi }{{15\sqrt{2}}}} \right)\mathbf{cm}{{\mathbf{s}}^{{-\mathbf{1}}}} (c) \left( {\frac{\pi }{{15}}} \right)\mathbf{cm}{{\mathbf{s}}^{{-\mathbf{1}}}} (d) \left( {\frac{{\pi \sqrt{2}}}{{15}}} \right)\mathbf{cm}{{\mathbf{s}}^{{-\mathbf{1}}}}
Ans (b)
6.
A wheel is subjected to uniform angular acceleration about its axis. Initially its angular velocity is zero. In the first two second it rotates through an angle . In next two second it rotates through {{\theta }_{2}}. What is the ratio \frac{{{{\theta }_{2}}}}{{{{\theta }_{1}}}}?
(a) 4 (b) 3 (c) 2 (d) 1
Ans .(b)
7.
A particle is describing a circular path of radius 10m in time interval of every 2 s. The average angular speed of the particle during 4 s is
(a) \,\,\pi \,\,\mathbf{rad}\,{{\mathbf{s}}^{{-\mathbf{1}}}} (b) 4\,\,\pi \,\,\mathbf{rad}\,{{\mathbf{s}}^{{-\mathbf{1}}}} (c) 2\,\,\pi \,\,\mathbf{rad}\,{{\mathbf{s}}^{{-\mathbf{1}}}} (d) None of these
Ans (d)
8.
A body covers a distance of 5 m along a semicircular path. The ratio of distance to displacement is
(a) 11 : 7 (b) 12 : 7 (c) 8 : 3 (d) 7 : 5
Ans (a)
9.
A particle is moving eastward with a velocity of magnitude 5 m/s. In 10 second, the velocity just changes it direction to northward. The average acceleration in this time period is
(a)Zero (b) \frac{1}{{\sqrt{2}}}\,\,\mathbf{m/}{{\mathbf{s}}^{2}} towards north–west
(c) \frac{1}{{\sqrt{2}}}\,\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}} towards north – east (d) \frac{1}{2}\,\,\mathbf{m/}{{\mathbf{s}}^{\mathbf{2}}} towards north–west
Ans (b)
10.
Starting from rest, a particle rotates in a circle of radius R=\sqrt{2}\,\mathbf{m} with an angular acceleration \alpha =\frac{\pi }{4}\mathbf{rad/}{{\mathbf{s}}^{\mathbf{2}}}. The magnitude of average velocity of the particle over the time it rotates quarter circle is
(a) 1.5 m/s (b) 2 m/s (c) 1 m/s (d) 1.25 m/s
Ans (c)
Practice Questions (Level-2)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.


