Video Lecture
Practice Questions (Level-1)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-2)
Q.1
A flat circular coil of n turns, area A and resistance R is placed in a uniform magnetic field B. The plane of coil is initially perpendicular to B. When the coil is rotated through an angle of 180o about one of its diameter, a charge Q1 flows through the coil. When the same coil, after being brought to its initial position, is rotated through an angle of 360o about the same axis a charge Q2 flows through it. Then Q2/Q1 is
(a) 1 (b) 2 (c) 1/2 (d) 0
Ans. (d)
Q.2
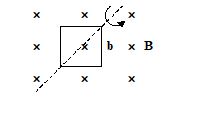
A square loop of side b is rotated in a constant magnetic field B at angular frequency w as shown in the figure. What is the emf induced in it?
(a) b2Bw sin wt
(b) bBw sin2 wt
(c) bB2w cos wt
(d) b2Bw
Ans. (a)
Q.3
If the flux of magnetic induction through a coil of resistance R and having n turns changes from f1 to f2, then the magnitude of the charge that passes through the coil is
(a) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{R}
(b) \frac{{n\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{R}
(c) \frac{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}{{nR}}
(d) \frac{{nR}}{{\left( {{{\varphi }_{2}}-{{\varphi }_{1}}} \right)}}
Ans. (b)
Q.4
A coil of 20×20 cm having 30 turns is making 30 rps in a magnetic field of 1 tesla. The peak value of the induced e.m.f. is approximately
(a) 452 V (b) 226 V (c) 113 V (d) 339 V
Ans. (b)
Q.5
In a uniform magnetic field of induction B, a wire in the form of semicircle of radius r rotates about the diameter of the circle with angular frequency w. If the total resistance of the circuit is R, the mean power generated per period of rotation is
(a) \frac{{B\pi {{r}^{2}}\omega }}{{2R}}
(b) \frac{{{{{(B\pi {{r}^{2}}\omega )}}^{2}}}}{{2R}}
(c) \frac{{{{{(B\pi r\omega )}}^{2}}}}{{2R}}
(d) \frac{{{{{(B\pi {{r}^{2}}\omega )}}^{2}}}}{{8R}}
Ans. (d)