Video Lecture
Theory For Making Notes
Heating Effects of Current
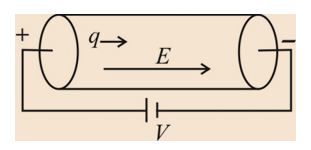
If under the influence of an electric field, charge q flows through a resistance R in time t when the potential difference across the resistance is V, the work done by the electric field on the charge
\displaystyle WD\,=\,V\,\times \,q\,\,=\,VIt [as \displaystyle I\,=\,\left( {q/t} \right)]
or WD = \displaystyle {{I}^{2}}Rt [as V=IR]
This work appears as thermal energy in the resistor. This is because the electrons accelerating by the applied field continuously lose their excess energy by collisions with the lattice. This in turn increases the thermal energy of lattice vibration and hence temperature of the resistor. So, the energy dissipated or the so called ‘heat produced’ by the resistance R :
\displaystyle H\,\,=\,\,WD\,\,=\,\,{{I}^{2}}\,Rt\,\,…(i)
This relation was first recognized and verified experimentally by Joule and so is called ‘Joule heating’.
Regarding heating effect of current it is worth noting that :
1.
As \displaystyle H\,\propto \,{{I}^{2}}, heating effect of current is common to both DC and AC. This is why instruments and appliances such as filament bulb, heater, geyser, toaster, etc, work both on DC and AC.
2.
Joule heating effect is irreversible, i.e., on reversing the direction of current in a resistor instead of heating, cooling does not result.
3.
Due to Joule-heating, power consumed by a resistor R in watt will be
\displaystyle P\,\,=\,\,\frac{H}{t}={{I}^{2}}R\,=\,\frac{{{{V}^{2}}}}{R}\,=\,VI [as \displaystyle V\,\,=\,\,IR ] …..(ii)
So if resistances are connected in series, i.e., I is same \displaystyle P\propto \,R with \displaystyle V\propto \,R [ as V = IR]….(iii)
i.e., in series potential difference and power consumed will be more in larger resistance. However if resistances are connected in parallel, i.e., V is same
\displaystyle P\,\propto \,\frac{1}{R} with \displaystyle I\,\propto \,\frac{1}{R} [as V = IR] ………..(iv)
i.e., in parallel current and power consumed will be more in smaller resistance. This in turn implies that more power is consumed in larger resistance if resistances are in series and in smaller resistance if resistances are in parallel.
4.
For a given voltage V, P\propto I . So higher is the electric power of the device, larger is the electric current drawn by it. As heat produced H\propto {{I}^{2}} , therefore heat produced by these devices will be large.
Maximum power transfer theorem:
A cell of emf E and internal resistance ‘r’ is connected to a variable resistance ‘R’. Let us find the value of R such that power out put of the circuit will be maximum.
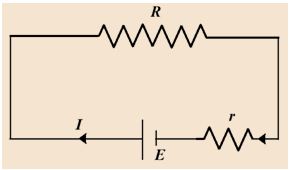
The current in the circuit is I=\frac{E}{{r+R}}.
Thus the power dissipated across R is {{P}_{{out}}}={{I}^{2}}R
{{P}_{{out}}}={{\left( {\frac{E}{{r+R}}} \right)}^{2}}R
For maximum value of {{P}_{{out}}}.
\frac{{d{{P}_{{out}}}}}{{dR}}=0 which results into r=R
and \frac{{{{d}^{2}}{{P}_{{out}}}}}{{d{{R}_{2}}}}<0 (confirms that {{P}_{{out}}} is maximum for r = R)
Power in Household Appliances
In any electrical installation, all the appliances are connected in parallel so that all of them get the same voltage. Furthermore, if one appliance is fused or gets out of order, the other keep operating.
Note the following important points about heating and power:
(1)
The power dissipated in a resistance R, when connected across a constant potential difference V, is
P=\frac{{{{V}^{2}}}}{R}
If R is changed to R/n, the power becomes
{P}’=\frac{{{{V}^{2}}}}{{(R/n)}}=n\frac{{{{V}^{2}}}}{R}=nP
Thus, if for a given voltage, resistance is changed from R to (R/n), power consumed changes from P to nP.
(2)
If n equal resistances are connected in series with a voltage source, the power dissipated is
{{P}_{\text{S}}}=\frac{{{{V}^{2}}}}{{nR}} [asRS = nR]
If the same resistance are connected in parallel with the same voltage source, the power dissipated becomes
{{P}_{\text{P}}}=\frac{{{{V}^{2}}}}{{(R/n)}}=\frac{{n{{V}^{2}}}}{R} [asRP = (R/n)]
So \frac{{{{P}_{\text{P}}}}}{{{{P}_{\text{S}}}}}={{n}^{2}} or PP = n2PS
Thus, the power consumed by n equal resistors in parallel is n2 times that of power consumed in series if V remains same.
(3)
For an electric appliance, there is specified power PS that is consumed by it when specified voltage VS is applied across it. If R is its resistance, then \displaystyle {{P}_{s}}=\frac{{V_{s}^{2}}}{R}
So if we compare two devices one of low electric power and another of high electric power each connected across the same source (same Vs) then high electric power device will have low resistance as compared to low electric power device, e.g., resistance of 100 W bulb is smaller than the resistance of 25 W bulb when connected to same supply (or in parallel)
Note that if the applied voltage VA is more than the specified voltage VS, the appliance may get damaged. However, if it is run at a reduced voltage, the power also gets reduced. Lets calculate the new power when we apply voltage VA.
P=\frac{{V_{\text{A}}^{2}}}{R}\text{ but R=}\frac{{V_{s}^{2}}}{{{{P}_{s}}}}\text{ }
Hence P=\frac{{V_{\text{A}}^{2}}}{{V_{\text{S}}^{\text{2}}/{{P}_{S}}}}={{\left( {\frac{{{{V}_{\text{A}}}}}{{{{V}_{\text{S}}}}}} \right)}^{2}}{{P}_{S}}
(4)
Bulbs in Parallel
Usually in a house-wiring the bulbs (and also other appliances) are connected in parallel across the power mains. As
\displaystyle {{P}_{p}}=\frac{{V_{\text{S}}^{2}}}{R},\text{ }R\propto \text{ }\frac{1}{{{{P}_{p}}}}
That is, the higher the power (orwattage), the lower is the resistance.
Since the voltage across all bulbs is same, a bulb with lower resistance (i.e., higher power) will draw larger current.
(5)
Bulb in Series
When bulbs are connected in series, same current flows through all. The power in a bulb is
P = I2R i.e., P ∝ R
Thus, in series grouping of bulbs, bulb of greater Power (wattage) will give less bright light and will have lesser resistance and potential difference across it but same current.
(6)
Fuse Wire and its Function
Fuse wire is made of an alloy of lead (37%) and tin (63%).It is put in series with an appliance. It is a safety device which protects the appliance from getting damaged, by melting and opening the circuit whenever the current in the circuit exceeds a specific predetermined value due to any reason.
Characteristics of fuse wire:It should have
(i) High resistivity and
(ii) Low melting point
If current I flows through the fuse wire of resistance R, and H is the rate of loss of heat per unit area, then in steady state, we have
\displaystyle {{I}^{2}}R\,=\,HA\,\,\,\,\,or\,\,\,\,{{I}^{2}}\rho L/\pi {{r}^{2}}\,=\,H\,\times \,\,2\pi rL
or I ∝ r3/2
Thus, we find that the current capacity of a fuse is independent of its length and varies with its radius as r3/2
(7)
Heating element or heater wire:
The wire used as heater wire should produce large amount of heat. So it should be of high power, i.e., consume high power.
Characteristics of heater wire: It should have:
(i) High resistivity and
(ii) High melting point
H=\frac{{{{V}^{2}}t}}{R}=\frac{{{{V}^{2}}tA}}{{\rho l}}
\left[ {R=\frac{{\rho l}}{A}} \right]
Resistivity, \rho is kept high so that the length l of wire of a given cross–section A used to produce a given amount of heat should be small.
Illustration
For what value of R, the power out put by 5\Omega resistance will be maximum in the circuit shown.
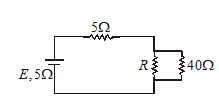
Solution:
Let us make an equivalent circuit of the given circuit as
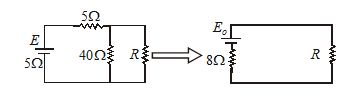
Now applying maximum power theorem R=8\Omega
Illustration
In the circuit shown in figure the heat produced in 5 ohm resistor due to current flowing through it is 10 calorie per sec. What is the heat dissipated in the 4 ohm resistor?
Solution:
As 5\Omega and (4+6)=10\Omega are in parallel and in parallel combination V is same with
P=({{V}^{2}}/JR)\,\,cal/\sec
\frac{{{{P}_{{10}}}}}{{{{P}_{5}}}}=\frac{{{{R}_{5}}}}{{{{R}_{{10}}}}}
i.e. {{P}_{{10}}}=\frac{5}{{10}}\times 10=5\,cal/\sec
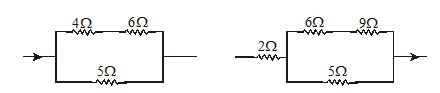
Now as 4\Omega and 6\Omega are in series and in series I is same with P=({{I}^{2}}R/J)\,cal/\sec , i.e.,
{{P}_{4}}+{{P}_{6}}=5cal/\sec with \frac{{{{P}_{4}}}}{{{{P}_{6}}}}=\frac{{{{R}_{4}}}}{{{{R}_{6}}}}=\frac{4}{6}=\frac{2}{3}
so, {{P}_{4}}+1.5\,{{P}_{4}}=5 i.e., {{P}_{4}}=2\,cal/\sec .
Illustration
Two wires made of tinned copper having identical cross–section ( ={{10}^{{-6}}}\,{{m}^{2}} ) and lengths 10 cm and 15 cm are to be used as fuses. Show that the fuses will melt at the same value of current in each case.
Solution:
Using R=\rho \frac{1}{a}=\rho \frac{1}{{\pi {{r}^{2}}}}
Heat produced per second =\rho \frac{1}{{\pi {{r}^{2}}}}\times {{l}^{2}}
Rate of loss of heat per unit surface area,
H=\frac{{{{I}^{2}}\rho \frac{1}{{\pi {{r}^{2}}}}}}{{2\pi rl}}=\frac{{{{I}^{2}}\rho }}{{2{{\pi }^{2}}{{r}^{3}}}} \left[ {I\,\,\propto \,\,{{r}^{{3/2}}}} \right]
Clearly H is independent of l
Both of the given fuses will melt at same value of current irrespective of their lengths.
Illustration
An electric bulb is rated as 240 V, 60 W. Find the resistance of its element and the current drawn by it, when operated at the rated voltage.
Solution
Since the power is the product of current and voltage, we have
Current I = \displaystyle \frac{P}{V}=\frac{{60}}{{240}} = 0.25 A
Using ohms’ law, the resistance of the bulb is
\displaystyle R=\frac{V}{I}=\frac{{240}}{{0.25}} = 960Ω
Illustration
Calculate the resistance of an electric heater that draws a current of 5 A from a 220 V supply. Also find the electrical energy consumed by it, if it runs continuously for 2 hours. How much will you have to pay for this energy if the rate is Rs.2.50 per unit ?
Solution
The resistance of the heater is given as
\displaystyle R=\frac{V}{I}=\frac{{220}}{5} = 44 Ω
The power of the heater is
P = VI = 220 x 5 = 1100 W
Therefore, the energy consumed in 2 hours is
K = P x t = 1100 x 2 = 2200 watt hour
= \displaystyle \frac{{2200}}{{1000}} kW h = 2.2 kW h
The cost of this energy = rate x total energy
= 2.50 x 2.2 = Rs.5.50
Illustration
You have two electric bulbs. The first is rated as 240 V, 60 W; and the second as 240 V, 120 W. (a) Compare their resistances. (b) If the two bulbs are put in series, and the combination connected across the 240 V power mains, which bulb lights brighter ?
Solution
The power of a bulb is given as
P=\frac{{{{V}^{2}}}}{R}
Therefore, for the first bulb, \displaystyle {{R}_{1}}=\frac{{V_{1}^{2}}}{{{{P}_{1}}}}=\frac{{240\times 240}}{{60}} = 960 W
And, for the second bulbs, \displaystyle {{R}_{2}}=\frac{{V_{2}^{2}}}{{{{P}_{2}}}}=\frac{{240\times 240}}{{120}}= 480 W
\displaystyle \frac{{{{R}_{1}}}}{{{{R}_{2}}}}=\frac{{960}}{{480}}=2
Note that the bulb with lower wattage (i.e., power rating) has higher resistance.
When the two bulbs are connected in series, the total resistance becomes
R = R1 + R2 = 960 + 480 = 1440 Ω
Therefore, the current drawn is
\displaystyle I=\frac{V}{R}=\frac{{240}}{{1440}} = 0.1666 A
The power expended in the two bulbs,
P1s = I2R1 = (0.1666)2 x 960 = 26.64 W
and, P2s = I2R2 = (0.1666)2 x 480 = 13.32 W
\displaystyle \frac{{{{P}_{{1s}}}}}{{{{P}_{{2s}}}}}=\frac{{26.64}}{{13.32}}=2
Note that when bulbs are connected in series, the bulb rated at lower power lights brighter.
Illustration
If two bulbs of 25 W and 100 W rated at 220 V are connected in series across a 440 V supply, will both the bulb fuse ? If not, which one ?
Solution
As for an electric appliance R= (V_{\text{S}}^{2}/{{W}_{S}}), so for same specified voltage VS,
\displaystyle \frac{{{{R}_{{25}}}}}{{{{R}_{{100}}}}}=\frac{{100}}{{25}}=4 i.e., R25 = 4R with
R100 = R
Now in series connection, potential divides in proportion to resistance.
So \displaystyle {{V}_{1}}=\frac{{{{R}_{1}}}}{{({{R}_{1}}+{{R}_{2}})}}V
i.e., \displaystyle {{V}_{{25}}}=\frac{4}{5}\times 440=352\text{ }V
And \displaystyle {{V}_{2}}=\frac{{{{R}_{2}}}}{{({{R}_{1}}+{{R}_{2}})}}V i.e., \displaystyle {{V}_{{100}}}=\frac{1}{5}\times 440=88\text{ }V
From this it is clear that voltage across 100 W bulb (= 88 V) is less than the specified (220 V), while across 25 W bulb (= 352 V) is greater than the specified (220 V), so 25 W bulb will fuse.
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
