Video Lecture
Theory For Making Notes
Heat transfer
Heat can be transferred from one place to another by three different methods, namely, conduction convection and radiation. Conduction usually takes place in solids, convection in liquids and gases, and no medium is required for radiation. Radiation is fastest and conduction is slowest.
Thermal conduction
This is the mode of heat transfer in which particles of the medium do not leave their position permanently i.e., they keep vibrating at their own places and transfer energy from one part of the medium to the other part.
Thermal conductivity
The ability of a material to conduct heat is measured by thermal conductivity of the material.
Consider a solid bar of thickness l and cross-sectional area A. Let the left side of the bar is at temperature T1 and right side at T2 where T1>T2.
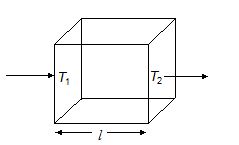
Sooner or later the temperature of each cross-section becomes constant with respect to time. This is known as steady state. If ΔQ amount of heat flows through a cross-section in time Δt under steady state conditions then the rate of heat transfer is given by
\frac{{\Delta Q}}{{\Delta t}}\,=\,\frac{{KA\,({{T}_{1}}-{{T}_{2}})}}{l}
whereK is a constant for the material of the rod and is called thermal conductivity of the material of the rod. It’s unit is J/s-m-K or Cal-s-m-K.
If the area of cross-section is not uniform or if the steady state conditions are not reached, then the equation can only be applied to a thin layer of material perpendicular to the heat flow. If A be the area of cross-section at a place, dx be a small thickness and dT be the temperature difference across the layer of thickness dx then the rate of heat transfer is
\frac{{dQ}}{{dt}}\,=\,-KA\,\frac{{dT}}{{dx}}
The negative sign indicates that \frac{{dT}}{{dx}} is negative along the direction of flow.
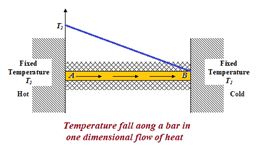
The diagram given below shows how the temperature falls linearly along the length of a bar when its ends are kept at different temperatures.
Thermal Resistance
In the equation \frac{{\Delta Q}}{{\Delta t}}\,=\,\,\frac{{{{T}_{1}}\,-\,{{T}_{2}}}}{{(\frac{l}{{KA}})}}
\frac{{\Delta Q}}{{\Delta t}} If we treat as thermal current and T1 – T2 as the temperature difference due to which the thermal current is flowing, then quantity \frac{l}{{KA}} can be treated as somewhat similar to electrical resistance (think i = \frac{V}{R}, Ohm’s law) and we call it thermal resistance. So thermal resistance of a body depends upon its length, area cross-section and thermal conductivity of the material of the body.
There exists an useful analog between thermal conductivity and electrical conductivity
Thermal Conduction \frac{{dQ}}{{dt}}=kA\left( {\frac{{{{T}_{1}}-{{T}_{2}}}}{l}} \right)
I = \frac{{dQ}}{{dt}}
RT = \frac{l}{{kA}}
I = \frac{{{{T}_{1}}-{{T}_{2}}}}{{{{R}_{T}}}} | Electrical Conduction \frac{{dq}}{{dt}}=\frac{A}{\rho }\left( {\frac{{{{V}_{1}}-{{V}_{2}}}}{l}} \right)
I = \frac{{dq}}{{dt}}
RE= \frac{{\rho \,l}}{A}
I = \frac{{{{V}_{1}}-{{V}_{2}}}}{{{{R}_{E}}}} |
Using the above analogy, a problem of heat conduction may be transformed into a problem of electrical conduction and can be easily solved using the formulae of electric circuits. Such as, for a series and parallel combination the equivalent resistance is defined as
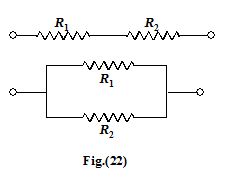
R = R1 + R2 (series)
\frac{1}{R}=\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}} (parallel)
Combination of Layers
Layers in series
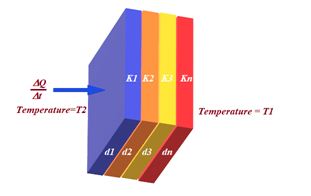
Let us consider a multiplayer medium consisted of layers having area of cross-section A each and width d1, d2, …dn as shown. The thermal conductivities of various layers are K1, K2 …, Kn. Remember in this case the same amount of heat flows through each layer.If a temperature difference of magnitude T2 – T1 is maintained between the near and far faces of the multiplayer (where T2 and T1 are the temperatures of the near and far faces respectively), then rate of heat flow is given by
\frac{{\Delta Q}}{{\Delta t}}\,=\,\frac{{A\,({{T}_{2}}-{{T}_{1}})}}{{\frac{{{{d}_{1}}}}{{{{k}_{1}}}}\,+\,\frac{{{{d}_{2}}}}{{{{k}_{2}}}}\,+\,…\,+\,\frac{{{{d}_{n}}}}{{{{k}_{n}}}}}}
Layers in parallel
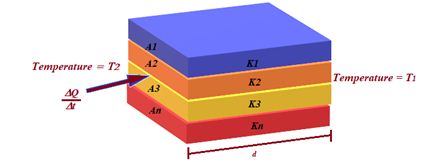
Now let us consider a multiplayer, this time having same width d but different areas of cross-section A1, A2, …An as shown. The thermal conductivities of the various layers are k1, k2, …kn. Remember in this case the rate of heat flow is different in different layers but the temperature difference is same across each layer. If a temperature difference of magnitude (T2 – T1) is maintained between the near and far faces of the multiplayer (where T2 and T1 are the temperatures of near and far faces respectively, then the total rate of heat flow is given by
\frac{{\Delta Q}}{{\Delta t}}\,\,=\,\,\frac{{({{T}_{2}}-{{T}_{1}})\,({{k}_{1}}{{A}_{1}}+{{k}_{2}}{{A}_{2}}+\,…\,+\,{{k}_{n}}{{A}_{n}})}}{d}
Detailed explanation of series and parallel combination can be found in video lectures
Illustration
Three rods of same length l and cross-sectional area A are joined in series between two heat reservoirs as shown in the figure. Their conductivities are 2K, K and K/2 respectively. Assuming that the conductors are logged from the surroundings find the temperatures T1and T2at the junction in the steady state condition.

Solution
The thermal resistance of the three conductors are
R1 = \frac{l}{{2KA}}
R2 = \frac{l}{{KA}}
R3 = \frac{{2l}}{{KA}}
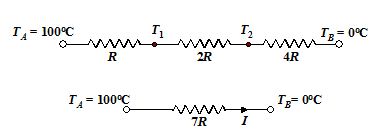
Let R1 =R then R2= 2R and R3 = 4R
Thus, the electric analogy of the heat conduction system is shown in the figure.
The equivalent resistance of the system is
Req = R + 2R + 4R = 7R
The heat current is
I = \frac{{{{T}_{A}}-{{T}_{B}}}}{{{{R}_{{eq}}}}}=\frac{{100-0}}{{7R}}=\frac{{100}}{{7R}}
The temperature T1 and T2 of the junction are
T1 = TA – IR = 100 – \left( {\frac{{100}}{{7R}}} \right)R=\frac{{600}}{7}\,\,oC
T2 = TA – I(R + 2R) = 100 – \left( {\frac{{100}}{{7R}}} \right)\left( {3R} \right)=\frac{{400}}{7}oC
Illustration
A double – pane window consists of two glass sheets each of area 1m2 and thickness 0.01 m separated by a 0.05 m thick stagnant air space. In the steady state, the room glass interface and the glass outdoor interface are at constant temperatures of 27°C and 0°C , respectively .
(a) Calculate the rate of heat flow through the window pane.
(b) Find the temperatures of other interfaces.
Take, thermal conductivities as Kglass= 0.8 Wm-1K-1
Kair = 0.08 Wm-1K-1

Solution
(a) Total thermal resistance is
R = \frac{{2{{t}_{1}}}}{{{{K}_{1}}{{A}_{1}}}}+\frac{{{{t}_{2}}}}{{{{K}_{2}}{{A}_{2}}}}
Here, A1 = A2= 1m2 , t1= 0.01 m, t2= 0.05 m ;
K1= 0.8 Wm-1K-1, K2= 0.08Wm-1K-1 .
R = \displaystyle \frac{{2\left( {0.01} \right)}}{{\left( {0.8} \right)\left( 1 \right)}}+\frac{{0.05}}{{\left( {0.08} \right)\left( 1 \right)}}=0.65{{W}^{{-1}}}K
Heat current = \frac{{dQ}}{{dt}}=\frac{{\Delta T}}{R}=\frac{{27-0}}{{0.65}}=41.5\,\,W
(b) T1 = 27 – \left( {\frac{{dQ}}{{dt}}} \right)\frac{{{{t}_{1}}}}{{{{K}_{1}}{{A}_{1}}}}=27-0.52={{26.48}^{\circ }}C
T2= 0 + \left( {\frac{{dQ}}{{dt}}} \right)\frac{{{{t}_{1}}}}{{{{K}_{1}}{{A}_{1}}}}={{0.52}^{\circ }}C
Illustration
An electric heater is used in a room of total wall area 137 m2 to maintain a temperature of 20°C inside it, when the outside temperature is –10°C. The walls have three different layers of materials. The innermost layer is of wood of thickness 2.5 cm, the middle layer is of cement of thickness 1.0 cm and the outermost layer is of brick of thickness 25.0 cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and the ceiling. The thermal conductivities of wood, cement and brick are 0.125 W/m-°C, 1.5 W/m-°C and 1.0 W/m–°C respectively.
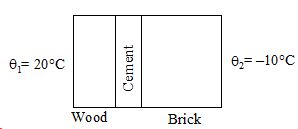
Solution:
The situation is shown in figure
thermal resistances of the wood, the cement and the brick layers are {{R}_{W}}\,=\,\frac{1}{K}\,\frac{x}{A}= \frac{\mathbf{1}}{{\mathbf{0}\mathbf{.125}\,\mathbf{W/m}-{}^\circ \mathbf{C}}}\,\frac{{\mathbf{2}\mathbf{.5}\,\times \mathbf{1}{{\mathbf{0}}^{{-\mathbf{2}}}}\mathbf{m}}}{{\mathbf{137}\,{{\mathbf{m}}^{\mathbf{2}}}}}
= \frac{{\mathbf{0}\mathbf{.20}}}{{\mathbf{137}}}\,{}^\circ \mathbf{C/W},
RC = \frac{\mathbf{1}}{{\mathbf{1}\mathbf{.5}\,\,\mathbf{W/m}-{}^\circ \mathbf{C}}}\,\,\frac{{\mathbf{1}\mathbf{.0}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{2}}}}\,\mathbf{m}}}{{\mathbf{137}\,{{\mathbf{m}}^{\mathbf{2}}}}} = \frac{{\mathbf{0}\mathbf{.0067}}}{{\mathbf{137}}}\,{}^\circ \mathbf{C/W}
andRB \,=\,\frac{\mathbf{1}}{{\mathbf{1}\mathbf{.0}\,\,\mathbf{W/m}-{}^\circ \mathbf{C}}}\,\,\frac{{\mathbf{25}\mathbf{.0}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{2}}}}\,\mathbf{m}}}{{\mathbf{137}\,{{\mathbf{m}}^{\mathbf{2}}}}}= \frac{{\mathbf{0}\mathbf{.25}}}{{\mathbf{137}}}\,\,{}^\circ \mathbf{C/W}
As the layers are connected in series, the equivalent R = Rw + RC + RB
= \frac{{0.20\,+\,0.0067\,+\,0.25}}{{137}}\,\,°C/W = 3.33 × 10–3 °C/W
The heat current is i\,=\,\frac{{{{\theta }_{1}}-{{\theta }_{2}}}}{R} = \frac{{\mathbf{20}\,{}^\circ \mathbf{C}\,-\,\mathbf{(}-\mathbf{10}{}^\circ \mathbf{C)}}}{{\mathbf{3}\mathbf{.33}\,\times \,\mathbf{1}{{\mathbf{0}}^{{-\mathbf{3}}}}{}^\circ \mathbf{C/W}}}\,= 9000 W
The heater must supply 9000 W to compensate the outflow of heat.
Illustration
The figure shows a large tank of water a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1 (<θ0). A metal rod of length L, area of cross-section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0). Specific heat capacity of water is s and all other heat capacities are negligible.
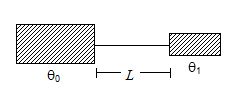
Solution:
Suppose, the temperature of the water in the smaller vessel is q at time t. In the next time interval dt, a heat, DQ is transferred to it where \Delta Q\,=\,\frac{{KA}}{L}\,({{\theta }_{0}}\,-\,\theta )\,dt … (i)
This heat increases the temperature of the water of mass m to (q + dq) where
ΔQ = ms dθ … (ii)
From (i) and (ii), \frac{{KA}}{L}\,({{\theta }_{0}}\,-\,\theta )\,dt= ms dq
or, dt = \frac{{Lms}}{{KA}}\,\frac{{d\theta }}{{{{\theta }_{0}}-\theta }} or, \int\limits_{0}^{T}{{dt\,=\,\frac{{Lms}}{{KA}}\,\int\limits_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}{{\frac{{d\theta }}{{{{\theta }_{0}}-\theta }}}}}}
whereT is the time required for the temperature of the water to become q2.
Thus, \mathbf{T}\,=\,\frac{{\mathbf{Lms}}}{{\mathbf{KA}}}\,\,\mathbf{ln}\,\,\frac{{{{\mathbf{\theta }}_{\mathbf{0}}}-{{\mathbf{\theta }}_{\mathbf{1}}}}}{{{{\mathbf{\theta }}_{\mathbf{0}}}-{{\mathbf{\theta }}_{\mathbf{2}}}}}
Illustration
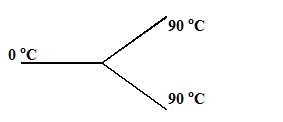
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at 0oC and 90oC respectively. The temperature of the junction of the three rods will be
(a) 45oC
(b) 60oC
(c) 30oC
(d) 20oC
Solution
Let θ be the temperature of the junction B.
Now, heat current in CB + heat current in DB
= heat current in BA (KCL)
\frac{{90-\theta }}{R}+\frac{{90-\theta }}{R}=\frac{{\theta -0}}{R}
θ = 60o
(b)
Illustration
Two identical conducting rods are first connected independently to two vessels, one containing water at 100oC and the other containing ice at 0oC. In the second case, the rods are joined end to end and connected to the same vessels. Let q1 and q2 g/s be the rate of melting of ice in the two cases respectively. The ratio q1/q2 is
(a)1/2
(b) 2/1
(c)4/1
(d) 1/4
Solution
The rate of the melting of the ice will be inversely proportional to the equivalent thermal resistance between the two vessels.
In the first case, equivalent thermal resistance is \frac{R}{2} and in the second case it is 2R. (whereR is the thermal resistance of the rod).
(c)
Illustration
Two bodies each having a heat capacity of C = 500 J/K are joined together by a rod of length L = 40.0cm, thermal conductivity 20 W/mK and cross-sectional area of S = 3.00 cm2. The bodies are joined with the help of a thermally insulated rod. The time after which temperature difference diminishes
h = 2 times is (Disregard the heat capacity of the rod)
(a) 193 minutes
(b) 240 minutes
(c) 77 minutes
(d) 144 minutes
Solution
-mc\frac{{d{{T}_{1}}\prime }}{{dt}}=\frac{{KA}}{l}({{T}_{1}}\prime -{{T}_{2}}\prime ) …(i)
mc\frac{{d{{T}_{2}}\prime }}{{dt}}=\frac{{KA}}{l}\left( {{{T}_{1}}\prime -{{T}_{2}}\prime } \right) …(ii)
From (i) and (ii) t=\frac{{mcl\ln 2}}{{2kA}}= 193 minutes
(a)
Illustration
A rod of length l (laterally thermally insulated) of uniform cross sectional area A consists of a material whose thermal conductivity varies with temperature as K=\frac{{{{K}_{o}}}}{{a+bT}} where K0, a & b are constants. T1 and T2 (<T1) are the temperature of two ends of rod. Then rate of flow of heat across the rod is
(a) \frac{{A{{K}_{0}}}}{{b\ l}}\left( {\frac{{a+b{{T}_{1}}}}{{a+b{{T}_{2}}}}} \right)
(b) \frac{{A{{K}_{0}}}}{{b\ l}}\left( {\frac{{a+b{{T}_{2}}}}{{a+b{{T}_{1}}}}} \right)
(c) \frac{{A{{K}_{0}}}}{{b\ l}}\ \text{ln }\left[ {\frac{{a+b{{T}_{1}}}}{{a+b{{T}_{2}}}}} \right]
(d) \frac{{A{{K}_{0}}}}{{a\ l}}\ \text{ln }\left[ {\frac{{a+b{{T}_{2}}}}{{a+b{{T}_{1}}}}} \right]
Solution
\frac{{dQ}}{{dt}}=-KA\frac{{dT}}{{dx}}
\frac{{dQ}}{{dt}}=-\frac{{{{K}_{0}}A}}{{a+bT}}\frac{{dT}}{{dx}}
\frac{{dQ}}{{dt}}\int\limits_{0}^{l}{{dx}}=-{{K}_{0}}A\int\limits_{{{{T}_{1}}}}^{{{{T}_{2}}}}{{\frac{{dT}}{{a+bT}}}}
\frac{{dQ}}{{dt}}= \frac{{A{{K}_{0}}}}{{b\ l}}\ \text{ln }\left[ {\frac{{a+b{{T}_{1}}}}{{a+b{{T}_{2}}}}} \right]
(c)
Convection
It is the mode of heat transfer by actual motion of matter. It is therefore possible only in fluids. Convection can be natural or forced. Gravity plays an important role in natural convection. Convection involves bulk transport of different parts of the liquid. We can see many examples of heat transfer by convection in our day to day life, right from the circulation of blood in our body to the intricacies of monsoon in India are all examples of convection.
Heat transfer through radiation
Radiation is the mode of heat transfer from one body to other even in the absence of any medium. Before discussing the laws governing radiation we have to understand following terms.
Black body: A black body may be defined as the one that completely absorbs the radiations of all wavelengths incident on it. The concept of black body is an idealised concept and in practice no substance behaves like black body.
Emissive power (e): The emissive power of a body is defined as the energy radiated per unit area per unit time, per unit solid angle perpendicular to the area for all possible wave length. So if energy radiated by the area ΔA of the surface in the solid angle ΔW in time Δt be ΔU the emissive power of the body is given by
E=\,\frac{{\Delta U}}{{(\Delta A)\,\,(\Delta W)\,\,(\Delta t)}}
The unit of emissive power is Joule/sec/m2 or watt/m2.
Absorptive power (a): Absorptive power of a body is defined as the fraction of the incident radiation that is absorbed by the body, in same time.
So, a = \frac{{\mathbf{Energy}\,\,\mathbf{absorbed}}}{{\mathbf{Energy}\,\mathbf{incident}}}
As the entire radiation incident a black body is absorbed, the absorptive power of black body is unity.
Kirchoff’s law of radiation
Kirchoff’s law states that ratio of the emissive power to the absorptive power for the radiation of a given wavelength is same for all bodies at the same temperature and is equal to the emissive power of a perfectly black body at that temperature. Kirchoff’s law in a way tells that a good emitter is a good absorber and a bad absorber is a bad emitter.
So, \frac{{e\,\,\mathbf{(body)}}}{{a\,\,\mathbf{(body)}}}= E (black body) = Constant (Depends of temperature)
Stefan’s law
The energy emitted per second per unit area of a black body is proportional to the fourth power of absolute temperature of the emitter, and is given by
E=\sigma {{T}^{4}} … (i)
wheres is a constant known as Stefan’s constant and its value is 5.67 × 10–8 J/m2-s-K4 For any other body
E=\in \,\sigma {{T}^{4}} … (ii)
Where \in is emissivity which is defined for a surface as the ratio of the emissive power of the surface to the emissive power of black body at the same temperature. The value of \in lies between 0 and 1, it is zero for perfectly reflecting surface and unity for black body.
Net Loss of Heat: The rate at, which a body radiates, is determined by the temperature of the body but the rate at which it absorbs energy by radiation depends on the temperature of surroundings.
So for a body at a temperature of T1 surrounded by walls at temperature T2 the net rate of loss of energy by radiation per unit area per second by radiation is given by
{{E}_{{net}}}=\in \sigma (T_{1}^{4}-T_{2}^{4})
This is also known as Stefan’s Boltzman law.
Newton’s law of cooling
For a small temperature difference between body and surrounding, the rate of cooling of the body is directly proportional to the temperature difference. This can be easily derived taking the value of T to be really close to temperature of surrounding To. Mathematically rate of fall of temperature with respect to time is given as
\displaystyle \frac{{dT}}{{dt}}=-ba(t-{{t}_{0}})
where b is a constant which depends on the nature of the surface involved and surrounding conditions, A is the surface area of the body and (T – T0) is the instantaneous temperature difference between the body and the surrounding. This is known as Newton’s law of cooling. The negative sign indicates that temperature decrease in time. This equation can be used in Celsius scale as well as in absolute scale because difference in temperature is same for absolute as well as for Celsius scale.
Spectral distribution of energy in a black body radiation
A black body emits radiations of different wavelength, however the energy content of radiations of different wavelength is not equal as shown in the graph given below. The relative intensities of different wavelengths depend upon the temperature of radiator
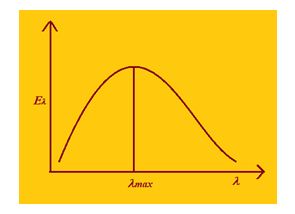
The following observations can be drawn from this diagram
(1)
For a given temperature the graph between energy and wavelength is a continuous arc spreading from a minimum to a maximum and has wavelength (lm) where the emission is maximum.
(2)
As the temperature increases the wavelength at which the emission is maximum, shifts to
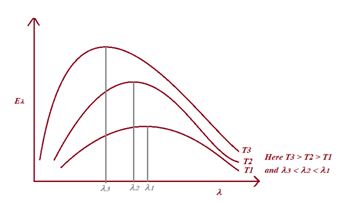
a lower values i.e., {{\lambda }_{m}}T=b where b is a constant having value 2.9 × 10–3 m-K, known as Wein’s constant. This is called Wein’s displacement law
(3)
As the temperature increases, the area enclosed by the curve also increases.
(4)
Area under the curve is proportional to T4 and hence verifies Stefan’s law.
Illustration
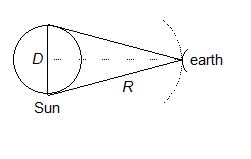
The earth receives solar radiation at a rate of 8.2 J/cm2 – minute. Assuming that the sun radiates like a blackbody. Calculate the surface temperature of the sun. The angle subtended by the sun on the earth is 0.53° and the Stefan constant s = 5.67 × 10-8 W/m2-K4
Solution:
Let the diameter of the sun be D and its distance from the earth be R. From the question,
\frac{D}{R}\,\approx \,\,0.53\,\times \,\frac{\pi }{{180}}= 9.25 × 10–3 … (i)
The radiation emitted by the surface of the sun per unit time is 4\pi \,{{\left( {\frac{D}{2}} \right)}^{2}}\,\sigma {{T}^{4}}\,=\,\pi {{D}^{2}}\sigma {{T}^{4}}.
At distance R, this radiation falls on an area 4pR2 in unit time. The radiation received at the earth’s surface per unit time per unit area is, therefore,
\frac{{\pi {{D}^{2}}\sigma {{T}^{4}}}}{{4\pi {{R}^{2}}}}\,=\,\frac{{\sigma {{T}^{4}}}}{4}\,{{\left[ {\frac{D}{R}} \right]}^{2}}
Thus, \frac{{\sigma {{T}^{4}}}}{4}\,{{\left[ {\frac{D}{R}} \right]}^{2}}\,=\,8.2J/m2 – minute
Or, \frac{1}{4}\,\times \,\left( {5.67\,\times \,{{{10}}^{{-8}}}\,\frac{W}{{{{m}^{2}}-{{K}^{4}}}}} \right)\,{{T}^{4}}\,\times \,{{(9.25\,\times \,{{10}^{{-3}}})}^{2}} = \frac{{8.2}}{{{{{10}}^{{-4}}}\,\times \,60\,}}\,\, \frac{W}{{{{m}^{2}}}}
or, T = 5794 K » 5800 K
Illustration
A copper sphere is suspended in a evacuated chamber maintained at 300 K. The sphere is maintained at constant temperature of 900 K by heating electrically. A total of 300 W electric power is needed to do this. When half of the surface of the copper sphere is completely blackened, 600 W is needed to maintain the same temperature of sphere. The emissivity of copper is
(a) 1/4
(b) 1/3
(c) 1/2
(d) 1
Solution
300=e\sigma A\left( {{{{900}}^{4}}-{{{300}}^{4}}} \right) … (i)
\displaystyle 600=\frac{{\sigma A}}{2}\left( {{{{900}}^{4}}-{{{300}}^{4}}} \right)+\frac{{e\sigma A}}{2}\left( {{{{900}}^{4}}-{{{300}}^{4}}} \right)… (ii)
e=\frac{1}{3}
(b)
Illustration
If the temperature of the sun is increased from T to 2T and its radius from R to 2R, then the ratio of the radiant energy received on earth to what it was previously will be
(a) 4
(b) 16
(c) 32
(d) 64
Solution
P\propto A{{T}^{4}} and A\propto {{r}^{2}}
P\propto {{r}^{2}}{{T}^{4}}
Now, T\prime =2T,\,\,r\prime =2r
Hence, P\prime =4\times 16P=64P
(d)
Illustration
Two spherical black bodies have maximum emission corresponding to wavelengths which are in the ratio of 2 : 3, and their radius 4 : 9. Then ratio of their emissive powers will be (assume same emissivity for body)
(a) 1 : 1
(b) \frac{{81}}{{16}}
(c) \frac{{16}}{{81}}
(d) \frac{8}{{27}}
\frac{{{{T}_{1}}}}{{{{T}_{2}}}}=\frac{{{{\lambda }_{2}}}}{{{{\lambda }_{1}}}}=\frac{3}{2}
\frac{{{{A}_{1}}}}{{{{A}_{2}}}}={{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}^{2}}=\frac{{16}}{{81}}
Solution
{{E}_{1}}=e\sigma A{{T}^{4}}
(a)
Illustration
Two spherical bodies of same mass and surface area raised to a temperature T are allowed to cool in the same environment. The curve of temperature versus time is as shown in the figure. Emissivity and absorbtivity are ex, ey and Ax and Ay respectively. Then
(a) ex>ey; Ax> Ay
(b) ex<ey‘; Ax> Ay
(c) ex>ey‘; Ax< Ay
(b) ex<ey‘; Ax< Ay
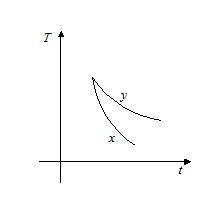
Solution
Rate of cooling
\frac{{dT}}{{dt}}=\frac{{eA}}{{mc}}\left[ {{{T}^{4}}-T_{o}^{4}\,} \right]\,\,
e ∝ \frac{{dT}}{{dt}}
Forx, \frac{{dT}}{{dt}} is more therefore {{e}_{x}}>{{e}_{y}}
and since absorbtivity is proportional to emissivity.
Hence {{A}_{x}} > {{A}_{y}}
(a)
Practice Questions (Level-1)
1.
A body cools from 90°C to 80°C in 10 minutes when the room temperature is 25°C. The same body will cool from 80°C to 70°C in
(a) 22.5 minutes
(b) 12 minutes
(c) 8\frac{1}{3}\ minutes
(d) 15 minutes
Ans (b)
2.
Two bodies A and B of same emissivity are placed in an evacuated vessel maintained at a temperature of 27°C. The temperature of A is 327°C and that of B is 127°C. The rates of heat loss from A and B will be nearly in the ratio
(a) 5 : 1
(b) 4 : 1
(c) 7 : 1
(d) 3 : 2
Ans (c)
3.
A cylindrical rod having temperature T1 and T2 at its end. The rate of flow of heat is Q1 cal/s. If all the linear dimensions are doubled keeping temperature constant, then rate of flow of heat Q2 will be
(a) 4Q1
(b) 2Q1
(c) \frac{{{{Q}_{1}}}}{4}
(d) \frac{{{{Q}_{1}}}}{2}
Ans(b)
4.
If K, \sigma and T stand for thermal conductivity, electrical conductivity and absolute temperature of a metal, then
(a) K+\sigma =T
(b) K-\sigma =T
(c) \frac{K}{\sigma }\propto T
(d) \frac{K}{\sigma }={{T}^{2}}
Ans (c)
5.
If wavelengths of maximum intensity of radiations emitted by Sun and Moon are metre and metre respectively, the ratio of their temperature is
(a) \frac{1}{{100}}
(b) \frac{1}{{200}}
(c) 100
(d) 200
Ans (b)
6.
On heating one end of a rod, the temperature of the whole rod will be uniform when
(a) K=1
(b) K=0
(c) K=100
(d) K=\infty
Ans (d)
7.
A container contains hot water at 100°C. If in time {{T}_{1}} temperature falls to 80°C and in time {{T}_{2}} temperature falls to 60°C from 80°C, then
(a) {{T}_{1}}={{T}_{2}}
(b) {{T}_{1}}>{{T}_{2}}
(c) {{T}_{1}}<{{T}_{2}}
(d) none of these
Ans (c)
8.
The wax melts up to lengths 105 cm and 60 cm for two identical rods of different metals in Ingen-Hauz experiment. The ratio of thermal conductivity of the two metals is
(a) 7 : 4
(b) 4 : 7
(c) 49 : 16
(d) 16 : 49
Ans (c)
9.
Two metal spheres of different radii are in thermal contact in vacuum as shown in figure. The spheres are at the same temperature. Which statement must be correct?

(a) Each sphere has the same internal energy
(b) There is no net transfer of thermal energy between the spheres
(c) Both spheres radiate electromagnetic energy at the same rate
(d) The larger sphere has a greater mean internal energy per atom then the smaller sphere.
Ans (b)
10.
A black metal foil is warmed by radiation from a small sphere at temperature T and at a distance d. The power received by the foil is P. If both the temperature and the distance are doubled, the power received by the foil will be
(a) 2 P
(b) 1 P
(c) 16 P
(d) 4 P
Ans (4)
11.
Water can be heated in cup of paper because
(a) paper is good conductor of heat
(b) paper has high specific heat
(c) paper is thin
(d) paper is good radiator of heat
Ans (c)
12.
A sphere, a cube and a disc all of the same material, quality and volume are heated to 600°C and left in air.Which of these will have the lowest rate of cooling?
(a) Sphere
(b) Cube
(c) Disc
(d) All will have same rate
Ans (a)
13.
Newton’s law of cooling is a special case of
(a) Stefan’s law
(b) Boltzmann’s low
(c) Wien’s law
(d) Planck’s law
Ans (a)
Practice Questions (Level-2)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
