Video Lecture
Theory For Notes Making
GRAVITATIONAL POTENTIAL
At a point in a gravitational field, potential (V) is defined as the work done by the external agent against the gravitational field in bringing unit mass from infinity to that point without acceleration.
Mathematically ,
V = \frac{W}{m}
It is a scalar having dimensions [L2 T–2] and SI unit J/kg.
⇒By the definition of potential energy , U = W
So, V = \frac{U}{m}
i.e., U = mV
Thus, gravitational potential at a point represents potential energy of a unit point mass at that point.
⇒By definition of work W = \displaystyle \int_{{}}^{{}}{{{{{\overset{\to }{\mathop{F}}\,}}_{{ext}}}}}
But, {{\overset{\to }{\mathop{F}}\,}_{{ext}}}=-{{\overset{\to }{\mathop{F}}\,}_{{gravitation}}}
W = -\int_{{}}^{{}}{{{{{\overset{\to }{\mathop{F}}\,}}_{{gravitational}}}.d\overset{\to }{\mathop{r}}\,}}
So, V=-\frac{{\int_{{}}^{{}}{{{{{\overset{\to }{\mathop{F}}\,}}_{{gravitational}}}.d\overset{\to }{\mathop{r}}\,}}}}{m}=-\int_{{}}^{{}}{{\overset{\to }{\mathop{E}}\,d\overset{\to }{\mathop{r}}\,}} \left[ {\because \ \frac{{{{{\overset{\to }{\mathop{F}}\,}}_{{gravitational}}}}}{m}=\overset{\to }{\mathop{E}}\,} \right]
i.e., dV = –Edr or E=-\frac{{dV}}{{dr}} here \frac{{dV}}{{dr}} is called potential gradient and in graphical terms it is also called the slope of potential vs position graph
So the potential can also be defined as a scalar function of position whose negative gradient, i.e., space derivative gives field intensity.
Also Negative of the slope of Vvsr graph gives field intensity.
Calculation of Gravitational Potential
(a) Gravitational potential at a point due to a point mass
We have, gravitational field due to a point mass E=-\frac{{GM}}{{{{r}^{2}}}}
[The negative sign is used as gravitational force is attractive]
V=-\int_{{}}^{{}}{{Edr=-\frac{{GM}}{r}+C}}
when, r = ∞, V = 0; so C = 0
\displaystyle V= \displaystyle -\frac{{GM}}{r}
(b) Gravitational potential due to a homogeneous solid sphere
Case I: When the point P lies outside the sphere
Consider a homogenous solid sphere of mass M and radius ‘R’. P is a point at a distance ‘r’ from the center of the sphere.
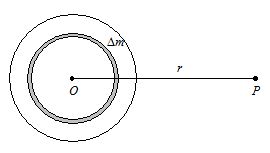
The solid sphere may be supposed to be made up of large number of thin concentric spherical shells. Consider one such shell of mass Δm
The potential at P due to the shell = – \frac{{G\ \Delta m}}{r}
So, the potential at P due to the entire sphere.
V=-\sum{{\frac{{G\ \Delta m}}{r}=-\frac{G}{r}\,\,\sum\nolimits_{{}}{{\Delta m}}}}
V=-\frac{{GM}}{r} [ QM = SDm]
Hence for an external point, a solid sphere behaves as if the whole of its mass is concentrated at the centre.
Case II: When the point P lies inside the sphere
Let us consider a concentric spherical surface thorough the point P. The potential at P arises out of the inner sphere and the outer thick spherical shell.
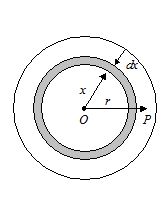
V = V1 + V2, where V1 =potential due to the inner sphere and V2 = potential due to the outer thick shell.
The mass of the inner sphere = \frac{{4\pi {{r}^{3}}}}{3}\rho , where
r = density of the sphere = \frac{M}{{\frac{4}{3}\pi {{R}^{3}}\ }}=\frac{{3M}}{{4\pi {{R}^{3}}}}
The potential at P due to this sphere
{{V}_{1}}=-\frac{{G\left[ {\frac{{4\pi {{r}^{3}}}}{3}} \right]\rho }}{r}=-\frac{{4\pi G\rho }}{3}{{r}^{2}} … (i)
To find V2, consider a thin concentric shell of radius x and thickness dx.
The volume of the shell = 4p x 2d x
The mass of the shell = 4p x2d xr.
The potential at P due to this shell
{{V}_{2}}=-\,\int\limits_{r}^{R}{{4\pi G\rho x\ dx}}
=-4\pi G\rho \ \left[ {\frac{{{{x}^{2}}}}{2}} \right]_{r}^{R}=-4\pi G\rho \,\left[ {\frac{{{{R}^{2}}}}{2}-\frac{{{{r}^{2}}}}{2}} \right] -2\pi G\rho \ \left[ {{{R}^{2}}-{{r}^{2}}} \right]
V1 + V2 = -\frac{{4\pi G\rho \,{{r}^{2}}}}{3}-2\pi G\rho \ \left[ {{{R}^{2}}-{{r}^{2}}} \right]
=-\frac{{4\pi G\rho }}{3}\left[ {{{r}^{2}}+\frac{{3{{R}^{2}}}}{2}-\frac{{3{{r}^{2}}}}{2}} \right]
=-\frac{{4\pi G\rho }}{3}\left[ {\frac{{3{{R}^{2}}}}{2}-\frac{{{{r}^{2}}}}{2}} \right]
=-\frac{{4\pi G}}{3}.\frac{{3M}}{{4\pi {{R}^{3}}}}\,\left[ {\frac{{3{{R}^{2}}-{{r}^{2}}}}{2}} \right]
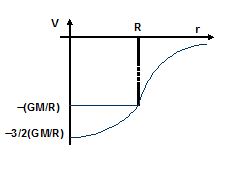
or, V=-\frac{{GM}}{{2{{R}^{3}}}}\,\left[ {3{{R}^{2}}-{{r}^{2}}} \right]
at center (r = 0) V=-\frac{{3GM}}{{2{{R}^{{}}}}}
GRAVITATIONAL POTENTIAL ENERGY
The potential energy of a system corresponding to a conservative force is defined as
\int\limits_{{{{U}_{i}}}}^{{{{U}_{f}}}}{{dU}}\,\,=\,\,-\,\int\limits_{{}}^{{}}{{\overset{\to }{\mathop{F}}\,.\,\,\overset{\to }{\mathop{{dr}}}\,}}
i.e., The change in potential energy is equal to negative of work done
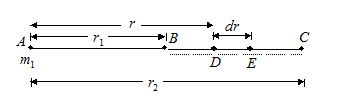
Let a particle of mass m1 be kept fixed at point A and another particle of mass m2 is taken from a point B to C. Initially, the distance between the particle is r1& finally it becomes AC = r2. We have to calculate the change in gravitation in potential energy of the system of two particles.
Consider a small displacement when the distance between the particles changes from r to r + dr. In the figure this corresponds to the second particle going from D to E.
Force acting on second particle is
\overset{\to }{\mathop{F}}\,\,=\,\frac{{G{{m}_{1}}{{m}_{2}}}}{{{{r}_{2}}}}along \overset{\to }{\mathop{{DA}}}\,
dW = \overset{\to }{\mathop{F}}\,.\,\overset{\to }{\mathop{{dr}}}\, = – \frac{{G{{m}_{1}}{{m}_{2}}}}{{{{r}^{2}}}}\,dr
dU = – dW = \int{{\frac{{G{{m}_{1}}{{m}_{2}}\,\,dr}}{{{{r}^{2}}}}}}
\int\limits_{{{{r}_{1}}}}^{{{{r}_{2}}}}{{dU}}\,=\,G{{m}_{1}}{{m}_{2}}\,\int\limits_{{{{r}_{1}}}}^{{{{r}_{2}}}}{{\frac{{dr}}{{{{r}^{2}}}}}}= G{{m}_{1}}{{m}_{2}}\,\left( {-\frac{1}{r}} \right)_{{{{r}_{1}}}}^{{{{r}_{2}}}}
U(r2) – U(r1) = Gm1m2 \left( {\frac{1}{{{{r}_{1}}}}\,-\,\frac{1}{{{{r}_{2}}}}} \right) … (i)
We choose the potential energy of the two particles system to be zero when the distance between them is infinity. This means U( \infty ) = 0
Hence U(r) = U(r) – U( \infty )
Now in equation (i)
Take r1 = r and r2 = \infty
U( \infty ) – U(r) = Gm1m2 \left( {\frac{1}{r}\,-\,\frac{1}{\infty }} \right) \ U(r) = -\,\frac{{G{{m}_{1}}{{m}_{2}}}}{{{{r}_{1}}}}
Hence when two masses m1 and m2 separated by a distance their gravitational potential energy is U(r) = \frac{{-G{{m}_{1}}{{m}_{2}}}}{r}
Example-4:
Three particles each of mass m are placed at the corners of an equilateral triangle of side d. Calculate
(a) the potential energy of the system,
(b) work done on the system if the side of the triangle is changed from d to 2d.
Solution:
(a) U=-\frac{{3Gmm}}{d} \displaystyle =-\frac{{3G{{m}^{2}}}}{d}
(b) {{U}_{i}}=-\frac{{3G{{m}^{2}}}}{d}, {{U}_{f}}=-\frac{{3G{{m}^{2}}}}{{2d}}
Work done =w=\Delta U={{U}_{f}}-{{U}_{i}}
Illustration
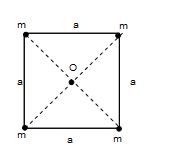
Find the potential energy of a system of four particles each of mass m placed at the vertices of a square of side a. Also find gravitational potential at the center of square.
Solution:
(i) Potential energy
= – \displaystyle \frac{{Gmm}}{a}-\frac{{Gmm}}{a}– \displaystyle \frac{{Gmm}}{a}-\frac{{Gmm}}{a}– \displaystyle \frac{{Gmm}}{{\sqrt{2}a}}-\frac{{Gmm}}{{\sqrt{2}a}}
= – \displaystyle \frac{{4G{{m}^{2}}}}{a}-\sqrt{2}\frac{{G{{m}^{2}}}}{a}
= – \displaystyle \frac{{G{{m}^{2}}}}{a}[4+\sqrt{2}]
(ii) Gravitational potential
V = \displaystyle -\frac{{Gm}}{{a/\sqrt{2}}}-\frac{{Gm}}{{a/\sqrt{2}}}-\frac{{Gm}}{{a/\sqrt{2}}}-\frac{{Gm}}{{a/\sqrt{2}}}
=- \displaystyle \frac{{4\sqrt{2}Gm}}{a}.
Illustration
Find the gravitational potential at a point where the gravitational field intensity is zero due to two particles of masses m1 = 1 kg and m2 = 4 kg separated through a distance l = 3 m?
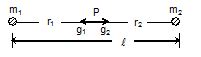
Let the gravitational field intensity due to the point masses m1 and m2 be zero at P
⇒ gp = 0 ⇒ |g1 + g2| = 0
⇒ g1 = g2 (numerically)
⇒ \displaystyle \frac{{G{{m}_{1}}}}{{{{x}^{2}}}}= \displaystyle \frac{{G{{m}_{2}}}}{{{{{(\ell -x)}}^{2}}}}
⇒ \displaystyle \frac{1}{{{{x}^{2}}}}= \displaystyle \frac{4}{{{{{(3-x)}}^{2}}}}
⇒ \displaystyle \frac{{3-x}}{x}= ±2
⇒ 3 – x = – 2x or, 3 – x = +2x
⇒ x = -3 (irrelevant) or x = 1
Vp = \displaystyle \left( {-\frac{{G{{m}_{1}}}}{x}} \right) + \displaystyle \left( {-\frac{{G{{m}_{2}}}}{{\ell -x}}} \right)
= – G \displaystyle \left[ {\frac{{{{m}_{1}}}}{x}+\frac{{{{m}_{2}}}}{{\ell -x}}} \right]
Putting G = 6.67 ´ 10-11 N-m2/kg2
m1 = 1 kg, m2 = 4 kg, l = 3 m, x = 1 m, we obtain,
Vp = -6.67 x 10–11 \displaystyle \left( {\frac{1}{1}+\frac{4}{{3-1}}} \right) J/kg
= -20.01 x 10-11 J/kg.
Escape Velocity
It is the minimum speed with which a body must be projected from the surface of a planet (usually the earth) so that it permanently overcomes and escapes from the gravitational field of the planet (the earth). We can also say that a body projected with escape speed will be able to go to a point which is at infinite distance from the earth.
If a body of mass m is projected with speed v from the surface of a planet of mass M and radius R, then
K.E. = \frac{1}{2}m{{v}^{2}}\ ;\ \ G.P.E.=-\frac{{GMm}}{R}
Total mechanical energy (T.M.E.) of the body = \frac{1}{2}m{{v}^{2}}-\frac{{GMm}}{R}
If the v’ is the speed of the body at infinity, then
T.M.E. at infinity = 0+\frac{1}{2}mv{{‘}^{2}}=\frac{1}{2}mv{{‘}^{2}}
Applying the principle of conservation of mechanical energy, we have
\frac{1}{2}m{{v}^{2}}-\frac{{GMm}}{R}=\frac{1}{2}mv{{‘}^{2}}
or, {{v}^{2}}=\frac{{2GM}}{R}+v{{‘}^{2}}
v will be minimum when v’→ o, i.e.,
{{V}_{e}}={{V}_{{\min }}}=\sqrt{{\frac{{2GM}}{R}}} =\sqrt{{2gR}}\ \ \ \ \ \ \left[ {\because \ g=\frac{{GM}}{{{{R}^{2}}}}} \right]
Important points
(i) Escape speed is independent of the mass and direction of projection of the body.
(ii) For earth as g = 9.8 m/s2 and R = 6400 km
{{V}_{e}}=\sqrt{{2\times 9.8\times 6.4\times {{{10}}^{6}}}}=11.2\ \text{km/s}
Illustration
What will be the escape speed on the surface of the moon if its radius were \frac{1}{4}th the radius of the earth and its mass \left( {\frac{1}{{80}}} \right)th the mass of the earth. Take escape velocity as 11.2 km/s on the surface of the earth. Given g(earth) = 9.8 m/s2.
Solution:
As on the surface of moon {{V}_{M}}=\sqrt{{\frac{{2G{{M}_{M}}}}{{{{R}_{M}}}}}}
Further, on earth the escape speed is {{V}_{E}}=\sqrt{{\frac{{2G{{M}_{E}}}}{{{{R}_{E}}}}}},
on dividing them
\frac{{{{V}_{M}}}}{{{{V}_{E}}}}=\sqrt{{\frac{{{{M}_{M}}}}{{{{M}_{E}}}}\times \frac{{{{R}_{E}}}}{{{{R}_{M}}}}}}=\sqrt{{\frac{1}{{80}}\times 4}}=\frac{1}{{\sqrt{{20}}}}
{{V}_{M}}=\frac{{{{V}_{E}}}}{{\sqrt{{20}}}}=\frac{{11.2}}{{4.47}} =2.5\ \text{km/s}
Objective Assignment
1.
The escape velocity of a particle of mass m varies as
(a) m2
(b) m
(c) mo
(d) m–1
Ans (c)
2.
Escape velocity of a projectile from the surface of earth is about
(a) 3 x 1010 cm/s
(b) 18600 m/s
(c) 25053.69 mph
(d) 42861 km/hr
Ans (c)
3.
In a gravitational force field a particle is taken from A to B along different paths as shown in the figure. Then
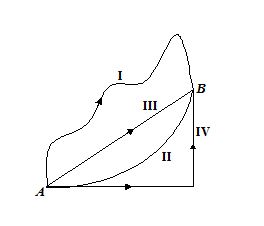
(a) work done along path I is more
(b) work done along path III is less
(c) work done along path IV is more
(d) work done along all paths is the same
Ans (d)
4.
If g is the acceleration due to gravity at the earth’s surface and r is the radius of the earth, the escape velocity for a body to escape out of earth’s gravitation field is
(a) \sqrt{{gr}}
(b) \sqrt{{2gr}}
(c) g/r
(d) r/g
Ans (b)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
