Video Lecture
Theory For Making Notes
Whenever the surface of a body slides over that of another, each body exerts a force of friction on the other, parallel to the surfaces. The force of friction on each body is in a direction opposite to its motion relative to the other body.
The force of friction comes into action only when there is a relative motion between the two contact surfaces or when an attempt is made to have it.
There are two types of sliding friction
(i) Static friction
The frictional force acting between any two surfaces at rest with respect to each other is called the force of static friction
(ii) Kinetic friction
The frictional force acting between surfaces in relative motion with respect to each other that is sliding over each other is called the force of kinetic friction or sliding friction
Graph between the applied force and the friction force acting on a body :
If a block of mass m placed on a rough surface is pulled by an external force F applied horizontally as shown in figure, then the friction force act on body against the external force F. The variation of friction force f with the external force F is shown in figure.
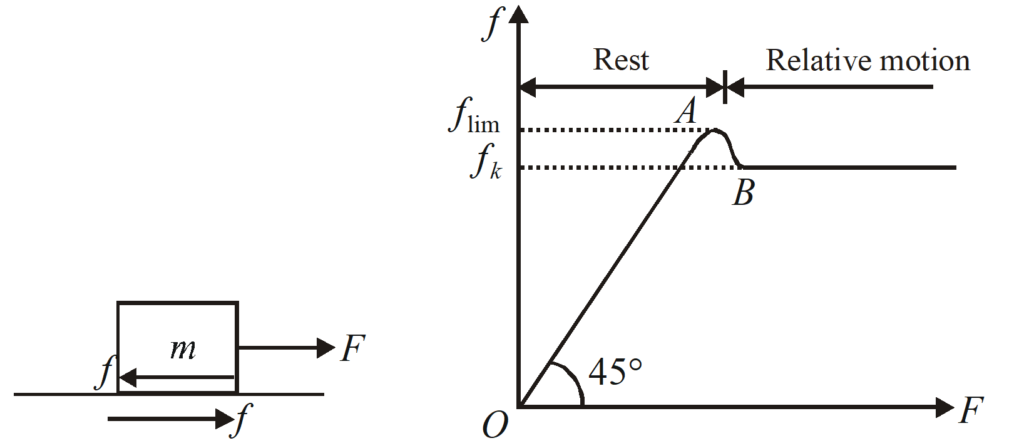
In region OA, the friction developed is equal in magnitude to applied force and keep the body at rest relative to the surfaces. Hence, the friction developed in the range is called static friction. And the maximum value of friction (static) which developed at point A is called limiting friction. Therare two points to be noted about the static friction {{f}_{s}}
(i) {{f}_{s}} = F (applied force or driving force) and
(ii) 0\le {{f}_{s}}\le {{f}_{{\max }}}\,(={{f}_{{\lim }}})
Beyond A, the friction decreases to B and then become constant. In this region the external force has greater value than friction so the block has relative motion i.e. sliding with respect to surface. The friction acting on moving body is called kinetic friction. Two points to be noted about the kinetic friction
(i) {{f}_{k}}\le F and
(ii) {{f}_{k}}=\text{constant}
Laws of friction
The empirical laws has been stated which help to understand friction and to assign the numerical value to the friction force. These laws can be stated as:
- The friction between two surfaces in contact is independent of the area of contact.
- The friction is independent of the relative speed of motion of bodies in contact as long as heating effects are negligible.
- The value of limiting force of friction is directly proportional to the normal force of interaction between the surfaces in contact i.e.,
{{f}_{{\lim }}}\propto N and {{f}_{{\lim }}}={{\mu }_{s}}N
where {{\mu }_{s}} is the coefficient of static friction.
- The value of kinetic force of friction acting on a moving body is again directly proportional to the normal force of interaction between the surfaces i.e.,
{{f}_{k}}\propto N and {{f}_{k}}={{\mu }_{k}}N
where {{\mu }_{k}} is the coefficient of kinetic friction.
- Note: The coefficient of static friction between a pair of surfaces is slightly greater than the coefficient of kinetic friction between that pair i.e., {{\mu }_{s}}\ge {{\mu }_{k}}
Microscopic Picture Of Friction
The friction is a consequence of the electromagnetic interaction between the atoms of body and surface in contact with it. Due to electromagnetic interaction, the cold welded bonds are formed between the microscopic points of contacts. The numbers of these microscopic points of contact is independent of the actual area of contact between body and surface but depends on the normal force of interaction between the surfaces.
To move a body relative to the surface, these cold welded bonds has to be broken by applying external force. The static friction that keeps the body at rest, unless an external force is not applied beyond limiting value of friction force, is a consequence of these cold welded bonds. Once these bonds get ruptured, the body start moving relative to the surface. But these bonds immediately get formed again and to keep the body in motion, a continuous a rupturing of these bonds is essential and hence a continuous external force is required. The friction provided by the reformation of cold welded bonds called as a kinetic friction.
Net Contact Forces and Angle of Friction
Whenever two bodies interact by direct contact of their surfaces, there are two contact forces acting on each body
- Normal Force N (perpendicular to surface of contact).
- Frictional Force f (Parallel to surface of contact)
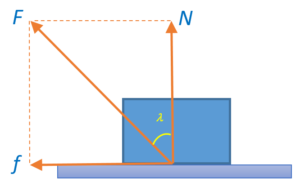
Since these two forces are perpendicular to each other hence the net contact force F is \sqrt{{{{N}^{2}}+{{f}^{2}}}}and the angle of friction \displaystyle \lambda is {{\tan }^{{-1}}}\frac{f}{N}.
for maximum friction \displaystyle \lambda is given by
\displaystyle {{\lambda}_{max}} = {{\tan }^{{-1}}}\left({\frac{{f}_{max}}{N}}\right)
\Rightarrow {{\lambda }_{{\max }}}={{\tan }^{{-1}}}\left( {\frac{{{{\mu }_{s}}N}}{N}} \right)
hence {{\lambda }_{{\max }}}={{\tan }^{{-1}}}\left( {{{\mu }_{s}}} \right)
It is important to note the following two points
(i) N\le F\le N\sqrt{{1+\mu _{S}^{2}}} and
(ii) \displaystyle O\le \lambda \le {{\tan }^{{-1}}}\left({{\mu }_{S}}\right)
Angle of Repose
Suppose a body is placed on an inclined surface whose angle of inclination \displaystyle \theta varies between 0 to \displaystyle \pi /2. The coefficient of friction between the body and the surface is \displaystyle \mu . Let the initial value of \displaystyle \theta be zero and if we slowly start increasing the value of \displaystyle \theta , then at a particular value of \displaystyle \theta =\phi the block just starts to move. This value of \displaystyle \theta =\phi is called the angle of friction.

Mathematically, if the block is stationary, then
\displaystyle mg\sin \theta ={{f}_{s}}
When the block is about to slide then \displaystyle \theta =\phi ,
and hence \displaystyle mg\sin \phi =f{}_{{\max }}
or \displaystyle mg\sin \phi ={{\mu}_{s}} N={{\mu}_{s}} mg\cos \phi
or \displaystyle \tan \phi ={{\mu}_{s}}
Thus \displaystyle \phi ={{\tan }^{{-1}}}{{\mu}_{s}}
Points to Remember
- The angle of friction is that minimum angle of inclination of the inclined plane at which a body placed at rest on the inclined plane is about to slide down.
- When \displaystyle \theta \le \phi \text{ (or ta}{{\text{n}}^{{-1}}}{{\mu}_{s}} ) the body is in static equilibrium.
- When the angle of inclination is more than the angle of friction \displaystyle (\theta >\phi ) the block starts sliding down with acceleration. And, if we wish to keep it in equilibrium an external force has to be applied.
A mass m rests on a horizontal surface. The coefficient of friction between the mass and the surface is µ. If the mass is pulled by a force F as shown in figure. The limiting friction between mass and the surface will be
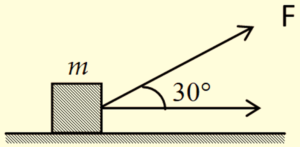
(a) \displaystyle \mu mg
(b) \displaystyle \mu \,\left[ {mg-\left( {\frac{{\sqrt{3}}}{2}} \right)\,F} \right]
(c) \displaystyle \mu \,\left[ {mg-\left( {\frac{F}{2}} \right)} \right]
(d) \displaystyle \mu \,\left[ {mg+\left( {\frac{F}{2}} \right)} \right]
Solution
Let N be the normal reaction, then
\displaystyle F\sin \theta +N=mg
or \displaystyle N=mg – F\sin {30}^{o}
hence limiting friction is = \displaystyle \mu N=\mu (mg-Fsin {{30}^{o}})=\mu (mg-F/2)
Hence answer is (c)
Illustration
A block of mass M = 10 kg is placed at rest on a horizontal surface with coefficient of friction µ = 0.3. Find the friction acting between the block and the surface if It is pulled with a horizontal force F. Where
(i) F = 20 N
(ii) F = 40 N
Solution
The maximum value of friction force is
\displaystyle {{f}_{{\max }}}=\mu N=\mu Mg
or \displaystyle {{f}_{{\max }}} = (0.3) (10) (10) = 30 N
(a) To keep the block stationary the magnitude of friction force should be f = F = 20 N since \displaystyle f<{{f}_{{\max }}}. Therefore the force of friction is f =20 N
(b) To keep the block stationary the magnitude of friction force should be f = F = 40 N. Since f cannot be more than fmax = 30 N, therefore, the force of friction is \displaystyle f={{f}_{{\max }}}=30 N
Note that in this case friction force is unable to keep the block stationary and the block accelerates with
a = \frac{{F\,-f}}{M}\,=\frac{{40\,-\,30}}{{10}}\,=1 m/s2.
Note that friction force is not always equal to µN. It is the limiting or maximum value of friction. At any stage friction may attain any value between 0 and µN.
Illustration
In the figure, the block rests on a horizontal surface and weighs 20 N. If there is no applied external force along the horizontal direction.
(a) Find the force exerted by the block on the table ?
If a horizontal force F is applied and this force is increased to 8 N before the block starts its motion along the horizontal surface. A force of 7 N can maintain the block in uniform motion, once it has been set in motion.
(b) Find the coefficient of static and kinetic friction.
(c) What is the force of friction when a horizontal force of 4 N is applied on it ?
Solution
(a) Since there is no external force acting on the block along the horizontal direction hence no friction force acts between the block and the table. The force of interaction between the block and the table is normal reaction N, which equals to weight of the block and hence the force exerted on the table by the block is 20 N.
(b) Since the relative motion starts as the horizontal force becomes equal to 8N, therefore, limiting static friction {{f}_{s}} is equal to 8N
i.e. {{f}_{s}}={{\mu }_{s}}\,\,N=8N
Since N = mg = 20N, therefore, {{\mu }_{s}}=\frac{8}{{20}}=0.4
Since 7N force is required to maintain the relative motion, therefore, the magnitude of kinetic friction is equal to 7N
i.e. {{f}_{k}}=7N
or {{\mu }_{k}}N=7
hence {{\mu }_{k}}=\frac{7}{{20}}=0.35
(c) Since applied force F<{{f}_{s}}=8N therefore the block does not have any relative motion, thus F-f=0\Rightarrow f=4N.
Illustration
A block of weight 5 N is pushed against a vertical wall by a force of 12 N. The coefficient of friction between the wall and the block is 0.6. Find the magnitude of the force exerted by the wall on the block ?
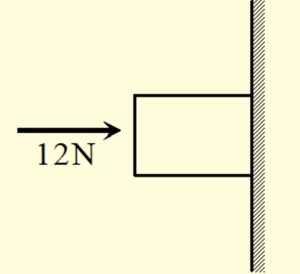
Solution
The net force F exerted by the wall on the block is the resultant of f and N.
12-R\Rightarrow R=12N
The limiting force of friction {{f}_{s}}={{\mu }_{s}}N=\left( {0.6} \right)\left( {12} \right)=7.2N
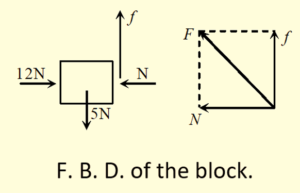
Here {{f}_{s}} is greater than the weight 5 N of the block hence the block doesn’t has any relative motion along the wall and the friction force acting between the block and the wall is 5 N. The force exerted by the wall on the block is F=\sqrt{{{{N}^{2}}+{{f}^{2}}}}=\sqrt{{{{{12}}^{2}}+{{5}^{2}}}}=13N
Illustration
For the system shown in the figure, the coefficient of static and kinetic friction between the block m2 and the horizontal surface is µs and µk.
If m2 = 10 kg, µs= 0.4 and µk = 0.35
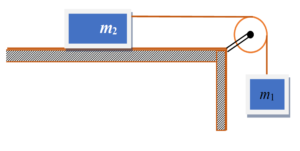
(a) find the maximum value of m1 so that the block m2 does not move.
(b) And also, if m1 = 5 kg, find the acceleration of the system.
Solution
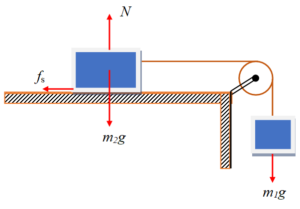
(a) The force which accelerates the system is m1g, while the opposing force is fs. For maximum value of m1 under equilibrium condition.
(m1g)max = fs max =µsm2g
or m1max = µsm2
here µs = 0.4, m2 = 10 kg
Thus, m1max = (0.4) (10) = 4 kg
(b) When m1 = 5 kg, the system starts accelerating; m1 accelerates downward and m2 accelerates rightward. Let a be the acceleration of the system, then
a = \frac{{{{F}_{{net}}}}}{{{{M}_{{system}}}}}\,=\frac{{{{m}_{1}}g-\,{{f}_{k}}}}{{{{m}_{1}}\,+{{m}_{2}}}}
or a = \left[ {\frac{{{{m}_{1}}\,-\,{{\mu }_{k}}\,{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right]\,g
Putting m1 = 5kg; m2 = 10 kg; µk = 0.35; g = 10 m/s2
we get, a = \left[ {\frac{{5-\left( {0.35} \right)\,(10)}}{{5\,+\,10}}} \right]\,(10) = 1 m/s2
Illustration
Two blocks of masses M1 and M2 are connected with a string which passes over a smooth pulley.
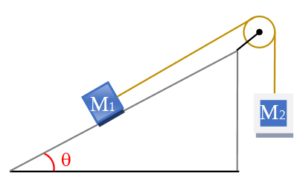
The mass M1 is placed on a rough inclined plane as shown in figure. The coefficient of friction between the block and the inclined plane is µ. What should be the minimum mass M2, so that the block M1 slides upwards?
(a) \displaystyle {{M}_{2}}={{M}_{1}}(\sin \theta +\mu \cos \theta )
(b) \displaystyle {{M}_{2}}={{M}_{1}}(\sin \theta -\mu \cos \theta )
(c) \displaystyle {{M}_{2}}=\frac{{{{M}_{1}}}}{{\left( {\sin \theta +\mu \cos \theta } \right)}}
(d) \displaystyle {{M}_{2}}=\frac{{{{M}_{1}}}}{{\left( {\sin \theta -\mu \cos \theta } \right)}}
Solution
The various forces acting on both the bodies is given below in the diagram
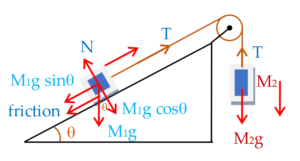
When the block M1 towards to move upward friction force on it acts downward and at the verge of sliding the friction force approaches the limiting value . Hence both the masses are in equilibrium and we have
\displaystyle T={{M}_{1}}g\sin \theta +f
and \displaystyle f=\mu {{M}_{1}}g\cos \theta
therefore \displaystyle T={{M}_{1}}g\sin \theta +\mu {{M}_{1}}g\cos \theta ) … (i)
Also \displaystyle T={{M}_{2}}g from mass \displaystyle {{M}_{2}} … (ii)
From (i) and (ii)
\displaystyle {{M}_{2}}g={{M}_{1}}g\sin \theta +\mu {{M}_{1}}g\cos \theta
or \displaystyle {{M}_{2}}={{M}_{1}}(\sin \theta +\mu \cos \theta )
So correct option is (a)
Illustration
A block of mass m is placed at rest on an inclined plane whose angle with the horizontal is more than the angle of friction ( \displaystyle \theta >\phi )
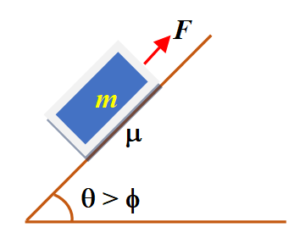
An external force parallel to the inclined plane is applied in the upward direction to keep it in equilibrium. Find the magnitude of the force F.
Solution
Since the block has a tendency to move downward, the force of friction acts upward on the block as shown in its free body diagram.
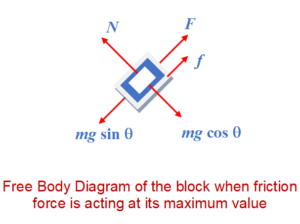
Applying equation of equilibrium, \displaystyle N=mg\cos \theta
\displaystyle {{F}_{\min}}+{{f}_{{\max }}}=mg\sin \theta
\displaystyle \Rightarrow {{F}_{\min}}=mg\sin \theta -{{f}_{{\max }}}
\displaystyle \Rightarrow {{F}_{\min}}=mg\sin \theta -\mu mg\cos \theta
\displaystyle Hence\text{ }{{F}_{\min}}=mg(\sin \theta -\mu \cos \theta )
Note that this is the minimum magnitude of force required to keep it in equilibrium. If we apply a force slightly more than this the block does not start moving up but the magnitude of the friction force gets reduced. It becomes equal to zero when the external force attain a value equal to \displaystyle F=mg\sin \theta .
If the force is increased further then the body has a tendency to move upward and hence friction starts acting down the plane. As the external force further increases the friction also increases upto its maximum value i.e. \displaystyle \mu N . Upto this instant the body remains stationary and the cooresponding external force is called the maximum force upto which the body remains in equilibrium. If the external force is further increased then the body starts moving up the plane. Hence the maximum force can be calculated using the following F.B.D. and applying condition of equilibrium.
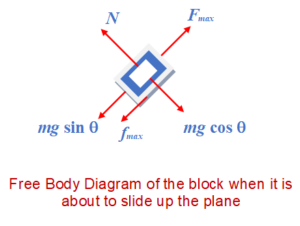
Now \displaystyle {{F}_{{\max }}}=mg\sin \theta +{{f}_{{\max }}},
\displaystyle \Rightarrow {{F}_{{max}}}=mg\sin \theta +\mu mg\cos \theta
\displaystyle Hence\text{ }{{F}_{{\max }}}=mg(\sin \theta +\mu \cos \theta )
So we can conclude that the block can be held stationary if the external force lies in a range i.e. is between \displaystyle {{F}_{{\min }}}\text{ }\!\!\And\!\!\text{ }{{F}_{{\max }}}.
hence \displaystyle {{F}_{{\min }}}\le \text{ F }\le \text{ }{{F}_{{\max }}}
Or \displaystyle mg(\sin \theta -\mu \cos \theta )\le F\le mg(\sin \theta +\mu \cos \theta )
Illustration
A body of mass m rests on a horizontal floor with which it has a coefficient of static friction {{\mu }_{S}}. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.
Solution
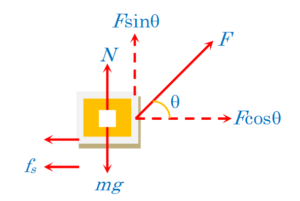
Let us first calculate F required to start the relative motion in terms of angle q. Considering the limiting equilibrium of the block in the horizontal and vertical direction, we get
N+F\sin \theta -mg=0 or N=mg-F\sin \theta
and F\cos \theta -{{f}_{s}}=0 or F\cos \theta ={{f}_{s}}={{\mu }_{s}}N
or F=\frac{{{{\mu }_{S}}mg}}{{\cos \theta +{{\mu }_{S}}\sin \theta }} ——-(1)
The above equation tells us about the force required to produce the relative motion as a function of \theta .
Now, we have to find the angle \theta for which this force F is minimum. For the force F to be minimum
\left( {\cos \theta +{{\mu }_{s}}\sin \theta } \right) must be maximum. i.e. \frac{d}{{d\theta }}(\cos \theta +{{\mu }_{S}}\sin \theta )=0
or -\sin \theta +{{\mu }_{s}}\cos \theta =0
or \tan \theta ={{\mu }_{s}}
or \sin \theta =\frac{{{{\mu }_{S}}}}{{\sqrt{{1+\mu _{S}^{2}}}}}
and \cos \theta =\frac{1}{{\sqrt{{1+\mu _{S}^{2}}}}}
Substituting these values in the equation (1) to get the minimum force
or {{F}_{{\min }}}=\frac{{{{\mu }_{S}}mg}}{{\sqrt{{1+\mu _{S}^{2}}}}} with \theta ={{\tan }^{{-1}}}{{\mu }_{s}}.
Note that the minimum force is required to pull the block at an angle equal to the angle of friction.
Illustration
A body of mass 5 ´ 10-3 kg is launched up on a rough inclined plane making and an angle of 300 with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
Solution

During ascent the friction force acts down the plane and during descent, the friction force Newton’s Second Law, acts up the plane
By applying Newton’s Second Law and acceleration of the block is given by
during the time of ascent as {{a}_{A}}=g\sin \theta +\mu g\cos \theta
during the time of descent as {{a}_{B}}=g\sin \theta -\mu g\cos \theta
If the block has travelled a distance x up the plane, then the time of ascent is {{t}_{A}}=\sqrt{{\frac{{2x}}{{{{a}_{A}}}}}} and the time of descent is {{t}_{B}}=\sqrt{{\frac{{2x}}{{{{a}_{B}}}}}}
or \frac{{{{t}_{A}}}}{{{{t}_{B}}}}=\sqrt{{\frac{{{{a}_{B}}}}{{{{a}_{A}}}}}}=\sqrt{{\frac{{g\left( {\sin \theta -\mu \cos \theta } \right)}}{{g\left( {\sin \theta +\mu \cos \theta } \right)}}}}
It is given that {{t}_{A}}=\frac{1}{2}t,
therefore \frac{{\left( {\sin \theta -\mu \cos \theta } \right)}}{{\left( {\sin \theta +\mu \cos \theta } \right)}}=\frac{1}{4}
Illustration
A block of mass 2 kg attached with a wall via a string placed on a rough inclined surface of inclination 30° as shown in figure. Find the tension in the string.
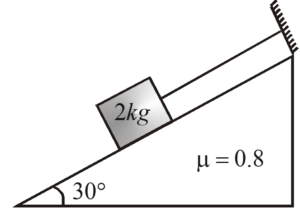
Solution
Since the angle of friction \phi ={{\tan }^{{-1}}}0.8=37{}^\circ which is greater than the angle of inclination, therefore the block is not be able to slide on the incline. Hence the tension in the string is absent i.e., the tension in the string is zero.
Illustration
Two blocks A and B are placed on a rough horizontal surface as shown in figure. The mass and the coefficient of friction of block A are 2 kg and 0.5 respectively, and that of B are 1.6 kg and 0.6 respectively. A force F is applied on A along the horizontal direction as shown in figure. Determine the net friction force exerted by surface on blocks when
(a) F = 8 N (b) F = 12 N (c) F = 20 N
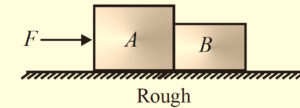
Solution
Since the surface is horizontal, so the normal reaction exerted by surface on blocks are equal to their respective weights. Therefore, the maximum friction forces exerted by surface on blocks are:
On block A: {{f}_{{A,\,\,\max }}}={{\mu }_{A}}{{m}_{A}}g=0.5\times 2\times 10=10\,\,\mathbf{N}
On block B: {{f}_{{B,\,\,\max }}}={{\mu }_{B}}{{m}_{B}}g=0.6\times 1\times 10=6\,\,\mathbf{N}
(a) Since F<10\,\,\mathbf{N}(={{f}_{{A,\,\,\max }}}), so the block A remains stationary and friction on A just balance the F. Thus, friction force on A is 8N while that on B is zero.
(b) Since F>10\,\,\mathbf{N}(={{f}_{{A,\,\,\max }}}), therefore the friction force acting on A is maximum i.e., {{f}_{A}}=10\,\,\mathbf{N}
Further F<16\,\,\mathbf{N}(={{f}_{A}}_{{,\,\,\max }}+{{f}_{B}}_{,}{{\,}_{{\,\max }}}), so the system of both the blocks remains stationary and the net friction force on both is equal to 12N. Thus, the friction on B is 12-10=2\,\,\mathbf{N}, which exist to balance reaction force exerted by A and B.
(c) Since F>16\,\,\mathbf{N}, so the system of blocks does not remain stationary. Thus the net maximum friction acts on system that is equal to 16 N.
Illustration
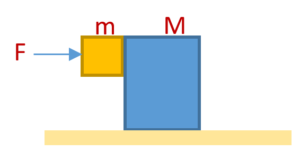
A plank of mass M is placed on a smooth horizontal surface with a block of mass m placed over it. The block and the plank have coefficient of friction \mu .
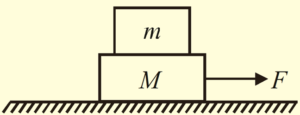
(a) If a constant horizontal force F is applied on plank and both the block and the plank start moving together with same acceleration a, find the value of a and the maximum value of force, say {{F}_{0}}, which keep the block to move together with the plank.
(b) What will be the acceleration of block and plank when force increased to new value equal to 2{{F}_{0}}?
Solution:
(a) Before the application of force F, both the block and the plank are at rest relative to each other as well as the ground. When force F is applied on plank, then it try to accelerate forward relative to block and ground both. Since ground is smooth so it cannot oppose its motion but block being rough oppose its motion by applying an opposing friction force f. The block also experience friction force provide by plank but in forward direction. Thus the friction force tends to retard plank and accelerate block as shown in figure.
When both the block accelerate together, then their common acceleration along horizontal is
a=\frac{F}{{m+M}} … (i)
The equation of motion for block m gives
f=ma or f=\frac{{mF}}{{m+M}}
The two blocks can move together only when friction acting between them is static and its value is below its maximum value i.e., f\le \mu {{N}_{1}}
Since block has equilibrium in the vertical direction, so {{N}_{1}}=mg. Therefore
f\le \mu mg
\Rightarrow \frac{{mF}}{{m+M}}\le \mu mg
or F\le \mu (m+M)g … (ii)
The maximum force {{F}_{o}} applied on plank without separating it from block is given by the equality of equation (ii).
Thus, {{F}_{0}}=\mu (m+M)g … (iii)
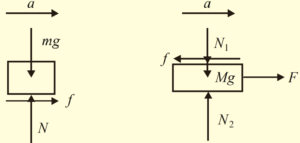
(b) Since the force applied exceed the value given in (iii) so the friction between plank and block is not sufficient to keep them at rest relative to each other. Therefore there is sliding of block over plank and thus the friction acting is equal to \mu mg.
Let {{a}_{1}} and {{a}_{2}} are the acceleration of block and plank relative to ground respectively, then their incomplete F.B.D. and equation of motion along horizontal direction suggest that:
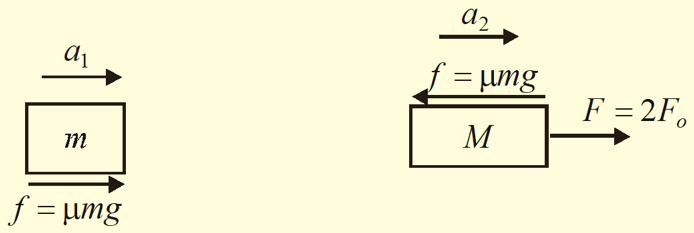
For block
f=m{{a}_{1}}
or \mu mg=m{{a}_{1}} \Rightarrow {{a}_{1}}=\mu g
For plank
F-f=m{{a}_{2}} or 2{{F}_{0}}-f=m{{a}_{2}}
or \frac{{2\mu (m+M)}}{g}-\mu mg=M{{a}_{2}} \Rightarrow {{a}_{2}}=\frac{{\mu (m+2M)}}{M}g
Practice Questions (Basic Level)
1.
Which of the following statements is not true
(a) The coefficient of friction between two surfaces increases as the surface in contact are made rough
(b) The force of friction acts in a direction opposite to the relative motion between two surfaces
(c) The limiting sliding friction depends on the area of contact
(d) Limiting friction depends on the normal contact force between the two surfaces
Ans (c)
2.
A given object takes n times as much time to slide down a 45° rough incline as it takes to slide down a perfectly smooth 45° incline. The coefficient of kinetic friction between the object and the incline is given by
(a) \left( {1-\frac{1}{{{{n}^{2}}}}} \right)
(b) \frac{1}{{1-{{n}^{2}}}}
(c) \sqrt{{\left( {1-\frac{1}{{{{n}^{2}}}}} \right)}}
(d) \sqrt{{\frac{1}{{1-{{n}^{2}}}}}}
Ans. (a)
3.
A box is placed on an inclined plane and has to be pushed down. The angle of inclination is
(a) Equal to angle of friction
(b) More than angle of friction
(c) Equal to angle of repose
(d) Less than angle of repose
Ans (d)
4.
A 60 kg body is pushed with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5 and 0.4 respectively. The acceleration of the body is
(a) 6 m/{{s}^{2}}
(b) 2 m/{{s}^{2}}
(c) 0 m/{{s}^{2}}
(d) 1 m/{{s}^{2}}
Ans (d)
5.
A block slides down an inclined plane of slope angle \theta with constant velocity. It is then projected up the same plane with an initial velocity vo. How far up the incline will it move before coming to rest.
(a)\frac{{v_{o}}}{{4g\sin \theta }}
(b)\frac{{v_{o}^{2}}}{{4g\tan \theta }}
(c)\frac{{v_{o}^{2}}}{{4g\sin \theta }}
(d)\frac{{v_{o}^{2}}}{{4g\cos \theta }}
Ans (c)
Question (6 to 8)
Block A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a massless, inextensible string and a frictionless pulley as shown in figure. The wedge is inclined at 45° to the horizontal on both sides. The coefficient of friction between block A and the wedge is 2/3 and that between block and the wedge is 1/3. If the system of A and B is released from rest, fin
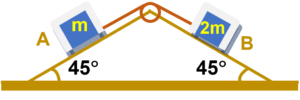
6.
the acceleration of A
(a)10
(b)2
(c)0
(d)1.25
Ans (c)
7.
tension in the string, and (a)
(a) \displaystyle \frac{{3\sqrt{2}}}{5}mg
(b) \displaystyle \frac{{2\sqrt{2}}}{3}mg
(c) \displaystyle \frac{{3\sqrt{2}}}{7}mg
(d) \displaystyle \frac{{5\sqrt{2}}}{3}mg
Ans (b)
8.
The magnitude and direction of the force of friction acting on A.
(a) \displaystyle \frac{{mg}}{{\sqrt{2}}}
(b) \displaystyle \frac{{mg}}{{5\sqrt{2}}}
(c) \displaystyle \frac{{mg}}{{\sqrt{3}}}
(d) \displaystyle \frac{{mg}}{{3\sqrt{2}}}
Ans (d)
Question (9 and 10)
A block rest on a rough inclined plane as shown. A horizontal force is applied to it
9.
Find out the force of reaction,
(a) \displaystyle N=mg\cos \theta +F\sin \theta
(b) \displaystyle N=mg\sin \theta -F\cos \theta
(c) \displaystyle N=mg\cos \theta +F\cos \theta
(d) \displaystyle N=mg\sin \{{90}^{o}} +F\cos \theta
Ans (a)
10.
Can the force of friction be zero if yes when ?
(a) No, if \displaystyle mg\sin \theta =F\cos \theta
(b)Yes, if \displaystyle mg\sin \theta =F\cos \theta
(c)yes, if \displaystyle mg\cos \theta =F\tan \theta
(d) No friction can’t be zero in any case
Ans (b)
Practice Questions (JEE Main Level)
1.
A hollow hemi sphere of radius a is fixed on the horizontal ground on its curved surface. How high from the bottom can a particle rest inside this hollow hemisphere if the coefficient of friction \displaystyle \mu =\frac{1}{{\sqrt{3}}}
(a)0.011 a
(b)0.134 a
(c)0.150 a
(d)1.0 a
Ans (b)
2.
The system shown below uses massless pulleys and rope. The coefficient of friction between the masses and horizontal surfaces is µ. Assume that M1 and M2 are sliding and gravity is directed downward.Find the tension in the rope.
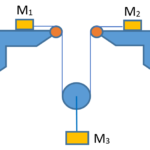
(a)\frac{{(\mu +1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{3{{M}_{2}}}}\,+\frac{1}{{3{{M}_{5}}}}}}
(b)\frac{{(\mu)\,g}}{{\frac{3}{{{{M}_{3}}}}\,-\,\frac{1}{{2{{M}_{1}}}}\,+\frac{2}{{1{{M}_{2}}}}}}
(c)\frac{{(\mu -1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{2{{M}_{1}}}}\,-\frac{2}{{1{{M}_{2}}}}}}
(d)\frac{{(\mu +1)\,g}}{{\frac{2}{{{{M}_{3}}}}\,+\,\frac{1}{{2{{M}_{1}}}}\,+\frac{1}{{2{{M}_{2}}}}}}
Ans (d)
3.
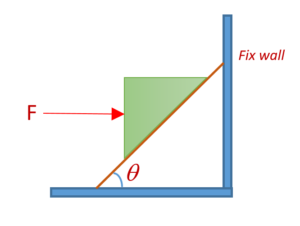
The coefficient of static friction between block and the horizontal surface is 0.25. Find the maximum weight of block A for which the system will be stationary. The block B weighs 700 N.
(a) 494 kg
(b) 500 N
(c) 100 kg
(d) 0 N
Ans (a)
4.
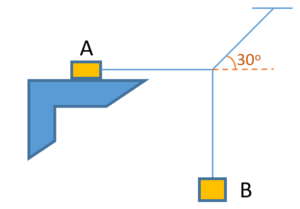
Two blocks with masses m and M are not attached. The coefficient of static friction between the blocks is µ and the horizontal surface is frictionless. What is the minimum magnitude of the horizontal force required to hold m against M during motion.
(a)\frac{{2M(M+m)g}}{{\mu m}}
(b)\frac{{m(M-m)g}}{{\mu M}}
(c)\frac{{m(2M+m)g}}{{\mu 2M}}
(d)\frac{{m(M+m)g}}{{\mu M}}
Ans (d)
Comprehension Based question ( 5 and 6)
A block of mass m = 2 kg is placed on a block of mass M = 4kg as shown in the figure.The coefficient of kinetic friction for all surfaces is µk =0.2. Ignore the masses of the pulley and the rope. For what value of the horizontal force F will the blocks
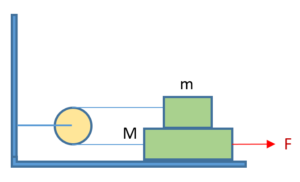
5.
move at constant speed
(a) 50N
(b) 30 N
(c) 20 N
(d) 0
Ans (C)
6.
accelerate at 2 m/s2
(a) 30 N
(b) 32 N
(c) 36 N
(d) 40 N
Ans (b)
Comprehension Based Question ( 7 to 9)
In the figure shown, the mass m2 = 10 kg slides on a frictionless table. The coefficients of static and kinetic friction between m2 and m1 = 5 kg are µs = 0.6 and µk = 0.4 . Take \displaystyle g=10\text{ }m/{{s}^{2}}
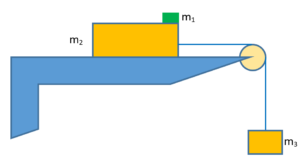
7.
What is the maximum acceleration of m1?
(a) 5 g
(b) 2 g
(c) 0.6 g
(d) 0.2 g
Ans (c)
8.
What is the maximum value of m3 if m1 moves with m2 without slipping ?
(a) 20.0 kg
(b) 22.5 kg
(c) 23.5 kg
(d) 25.0 kg
Ans (b)
9.
If m3 =30 kg, find the acceleration of each body and the tension in the string.
(a) 0.7 g for m2 and m3 , 1.4g for m1 , 9g N
(b) 0.7 g for m2 and m3 , 2.2g for m1 , 9g N
(c) 0.7 g for m2 and m3 , 0.8g for m1 , 9g N
(d) 0.7 g for m2 and m3 , 0.4 g for m1 , 9g N
Ans (d)
10.
A block rest on a rough inclined plane as shown. A horizontal force is applied to it

The maximum horizontal force required to keep the block at rest is
(a) \displaystyle {{F}_{{\max }}}=mg\tan (\theta -\phi )
(b) \displaystyle {{F}_{{\max }}}=mg\sin (\theta +\phi )
(c) \displaystyle {{F}_{{\max }}}=mg\tan (\theta +\phi )
(d) \displaystyle {{F}_{{\max }}}=mg\cos (\theta +\phi )
Ans (c)
Practice Questions (JEE Advance Level)
1.
In the figure shown two blocks of masses 3 kg and 5 kg are attached by a string and slide down a 30° incline. The coefficient of kinetic friction for the 3 kg block is 0.3. There is no friction between the 5 kg block and the incline. Find the acceleration of the blocks and the tension in the string.
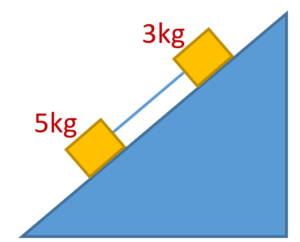
(a) ≈4 m/s2; 9 N
(b) ≈4 m/s2; N
(c) ≈4 m/s2; 5 N
(d) ≈4 m/s2; 4 N
Ans (c)
2.
In the arrangement shown in figure the bead of mass m can slide along the thread with some friction. The mass of the rod attached at the other end is M. The mass of the pulley and the friction in its axle are negligible. At the initial moment the bead is located opposite to the lower end of the rod. When set free, the bead gets opposite to the upper end of the rod in time t after the beginning of motion. Find the frictional force between the bead and the thread. The hanging portion of the rod is of length l.
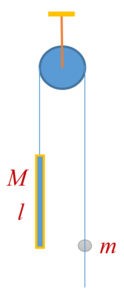
(a)\frac{{2Mml}}{{\left( {M-m} \right){{t}^{2}}}}
(b)\frac{{3Mml}}{{\left( {M-m} \right){{t}^{3}}}}
(c)\frac{{2Mml}}{{\left( {M+m} \right){{t}^{2}}}}
(d) \frac{{2Mml}}{{\left( {M-m} \right){{t}^{3}}}}
Ans (a)
3.
A crate slides down an inclined right-angled trough as shown in the figure. The coefficient of kinetic friction between the block and the material composing the trough is \displaystyle \mu k. Find the acceleration of the crate

(a)g\left( {\sin \theta -\sqrt{3}{{\mu }_{k}}\sin \theta } \right)
(b)g\left( {\sin \theta -\sqrt{2}{{\mu }_{k}}\sin \theta } \right)
(c)g\left( {\sin \theta -\sqrt{2}{{\mu }_{k}}\cos \theta } \right)
(d)g\left( {\sin \theta -\sqrt{3}{{\mu }_{k}}\cos \theta } \right)
Ans (c)
4.
What is the largest load C that can be suspended without moving blocks A and B ? The static coefficient of friction for all plane surfaces of contact is 0.3 . Block A weighs 500 N and block B weighs 700 N. Neglect friction in the pulley system.
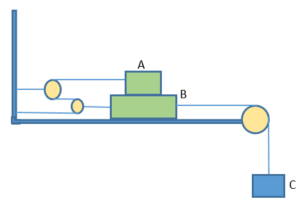
(a) 850 N
(b) 810 N
(c) 900 N
(d) 500 N
Ans (b)
5.
In the figure masses m1, m2 and M are 20 kg, 5 kg and 50 kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force is applied to the mass M. Take g = 10 m/s2.
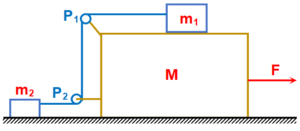
Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1 = 2f2. Find F , tension in the string and accelerations of the masses.
(a)F = 60 N, T = 18 N, a = 3/5 m/s2
(b)F = 50 N, T = 20 N, a = 3/5 m/s2
(c)F = 20 N, T = 15 N, a = 3/5 m/s2
(d)F = 10 N, T = 10 N, a = 3/5 m/s2
Ans (a)
6.
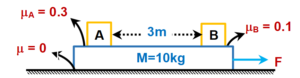
A plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA = 2 kg and mB = 1 kg lies at a distance of 3 m on the plank as shown in the figure. The friction coefficient between the blocks and plank are mA = 0.3 and mB = 0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
(a) 5 sec
(b) 2 sec
(c) 10 sec
(d) 6 sec
Ans (d)
7.
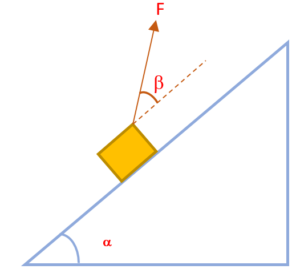
A block of mass m is pulled by means of a thread up an inclined plane forming an angle \displaystyle \alpha with the horizontal. The coefficient of friction is equal to m. Find the angle \displaystyle \beta which the thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to ?
(a) \displaystyle {{\tan }^{{-1}}}\ {{\sqrt{\mu}}} , \frac{{mg(\mu\sin \alpha \,+\, \cos \alpha )}}{{\sqrt{{1\,+{{\mu }^{2}}}}}}
(b) \displaystyle {{\tan }^{{-1}}}\ {{\mu}^{2}} , \frac{{mg(\sin \alpha \,+\,\mu \cos \alpha )}}{{\sqrt{{1\,+{{\mu }^{2}}}}}}
(c) \displaystyle {{\tan }^{{-1}}}\mu , \frac{{mg(\sin \alpha \,+\,\mu \cos \alpha )}}{{\sqrt{{1\,+{{\mu }^{2}}}}}}
(d) \displaystyle {{\tan }^{{-1}}}\mu , \frac{{mg(\cos \alpha \,-\,\mu \sin \alpha )}}{{\sqrt{{1\,+{{\ {\mu} }^{2}}}}}}
Ans (c)
8.
Two blocks A and B of equal masses are released from an inclined plane of inclination 45o at t = 0. Both the blocks are initially at rest. The coefficient of kinetic friction between the block A and the inclined plane is 0.2 while it is 0.3 for block B. Initially, the block A is √2 m behind the block B. When and where their front faces will come in a line. Take g = 10 m/s2.
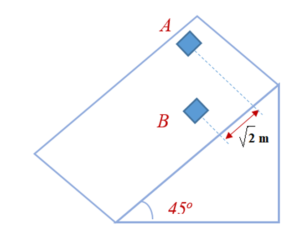
(a) 1s and 10.40 m
(b) 2 s and 11.313 m
(c) 5 s and 13.30 m
(d) 3 s and 11.00 m
Ans (b)
9.
A plank of mass 4m and length l is kept on a frictionless surface. A small block of mass m is kept on upper surface of plank at point A as shown in figure. Coefficient of friction between block and the plank is m. What minimum velocity must be given to the block in horizontal direction so that it just comes to the other end i.e. at point B of the plank?
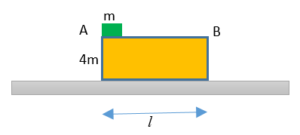
(a)\sqrt{{\frac{{5\mu gl}}{2}}}
(b)\sqrt{{\frac{{3\mu gl}}{3}}}
(c)\sqrt{{\frac{{7\mu gl}}{8}}}
(d)\sqrt{{\frac{{2\mu gl}}{9}}}
Ans (a)
10.
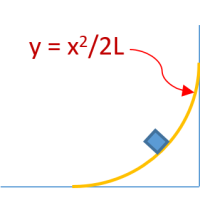
A ramp is constructed in parabolic shape such that the height y of any point on its surface is given in terms of the point’s horizontal distance x from the bottom of the ramp by y = x2/2L. A block of granite is to be set on the ramp’ the coefficient of static friction is 0.80. What is the maximum horizontal distance from the bottom of the ramp at which the block can be placed and remain at rest, if L = 10m?
(a) 8.5 m
(b) 8 m
(c) 9 m
(d) 9.4 m
Ans (b)




