Video Lecture
Theory For Making Notes
Reference Frame
A reference frame is a coordinate system with respect to which the motion of a body is considered. Consider the frame as an observer who observes the given body and calculate its displacement, velocity and acceleration with respect to itself.
In simple words the first step of solving a problem on mechanics is choosing a frame or observer relative to which the motion of a body should be described.
There are two types of reference frames
(i) Inertial frame
A reference frame in which Newton’s first law is valid is called an inertial reference frame. In an inertial reference frame, a body subject to no net force will either stay at rest or move at constant velocity.
Any frame moving at constant velocity relative to a known inertial frame is also an inertial frame. If the acceleration of a particle is zero in one inertial frame, it is zero in all inertial frames.
(ii) Non inertial frame
A reference frame which accelerates or rotates with respect to an inertial reference frame is called a non-inertial frame. Objects in non-inertial reference frames do not obey Newton’s law ( F = ma )
This equation sows that acceleration is not possible without a force. But in a non inertial frame if even no force is acting on the body actually we can observe acceleration in it. How?
Suppose you are sitting in an accelerating car along a straight line and you look at a tree on the road side. You will observe that the tree is moving backward with the same acceleration that you have due to acceleration of the car. Now you can understand that in your frame a tree is observed to be accelerating opposite to your motion even when there is no actual force acting on it. To explain the acceleration of the tree with respect to the you or your car (non-inertial frame) you have to apply a fictitious force called the pseudo force on the tree. It is an imaginary force which acts on all the occupants of an accelerated frame. The direction of the force is opposite to the direction of the acceleration. Hence
\displaystyle {{F}_{p}}=-ma
Where m is the mass of body (that is tree in our example) and `a’ be the acceleration of the reference frame ( that is car in the above example) .This pseudo force is real enough to throw you forward when a bus suddenly stops. It is fictitious in the sense that it has no physical origin, that is, it is not caused by one of the basic interactions in nature. Its action does not have the reaction required by the third law.
Mathematical explanation of pseudo force
Motion of a particle (P) is studied from two frames of references S and S’. S is an inertial frame of reference and S’ is a non inertial frame of reference. At any time, position vectors of the particle with respect to those two frames are \displaystyle \vec{r} and \displaystyle \vec{r}’ respectively. At the same moment position vector of the origin of S¢ is \displaystyle \vec{R} with respect to S as shown in the figure.
From the vector triangle OO’P , we get
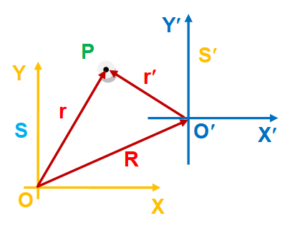
\displaystyle \vec{r}’=\vec{r}-\vec{R}
Differentiating this equation twice with respect to time we get
\displaystyle \frac{{{{d}^{2}}\vec{r}’}}{{d{{t}^{2}}}}=\frac{{{{d}^{2}}\left( {\vec{r}} \right)}}{{d{{t}^{2}}}}-\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {\vec{R}} \right)
hence \displaystyle \vec{a}’=\vec{a}-\vec{A}
Here
\displaystyle \vec{a}’= acceleration of the particle P relative to S’
\displaystyle \vec{a}= Acceleration of the particle relative to S
\displaystyle \vec{A}= Acceleration of S’ relative to S.
Multiplying the above equation by m (mass of the particle) we get
\displaystyle m\vec{a}’=m\vec{a}-m\vec{A}
hence
\displaystyle \vec{F}’={{\vec{F}}_{{\left( {real} \right)}}}-m\vec{A}
therefore
\displaystyle \vec{F}’={{\vec{F}}_{{\left( {real} \right)}}}+\left( {-m\vec{A}} \right).
Where F’ is the force as observed from non inertial frame S’. So in non-inertial frame of reference an extra force is taken into account in order to apply Newton’s laws of motion. The magnitude of this force is equal to the product of the mass of the body and acceleration of the frame and it is always directed opposite to the acceleration of the frame. This force is known as Pseudo force, because this force does not exist in the inertial frame of reference.
Note:
(i) When pseudo force is applied in equation of motion, then the acceleration obtained is with respect to a non-inertial frame of reference.
(ii) For problem solving purpose earth is assumed to be an inertial frame of reference.
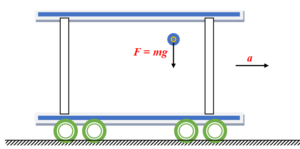
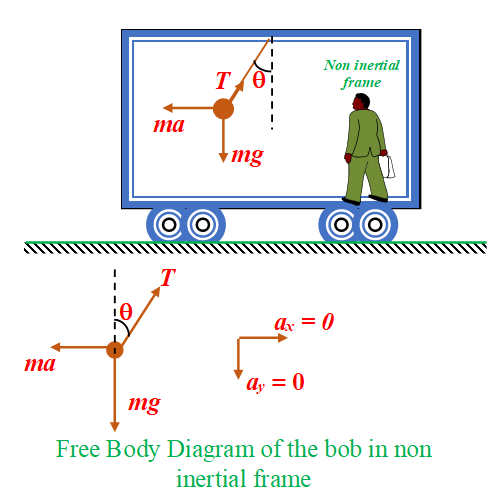
This ball is observed by two observers one standing on the ground and the other standing inside the accelerating cart. We know that the frame of that observer who is standing on the ground is an inertial frame.Whereas the frame of the second observer is a non inertial frame because he is accelerating.
Consider the diagram given below
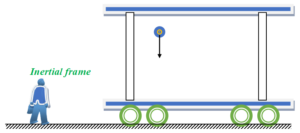
For an inertial frame the only force acting on the ball is the real force that is force of gravity (mg). Hence for this observer the ball appears to move vertically downward under the action of the gravitational force.
Now consider the non inertial frame that is the other observer standing inside the accelerating cart. For this noninertial frame there are two forces acting on the ball.
(i) real or actual force of gravity (mg)
(ii) pseudo or fictitious force (ma) opposite to the direction of acceleration of the observer.
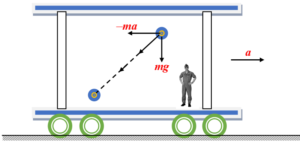
Hence for this non inertial frame the resultant of these two forces will decide the path of the ball. In other words the ball will follow the resultant force which makes some angle with vertical according to the law of parallelogram. Hence the ball appears to move in a straight line making an angle with the vertical as shown in the diagram given below
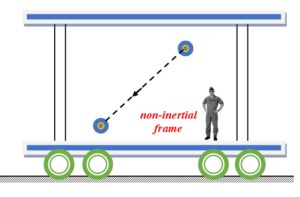
So it is clear that the motion of an object depends on the frame of reference. And in the non inertial frames always consider a pseudo force and involve it in your calculations as if it is actually acting on the object.
Concept of apparent weight in an accelerating lift.
Consider a man standing on a weighing mechine attached to the floor of a lift.

When the lift is stationary this can be considered as a inertial frame of reference and hence only real forces are suppose to be acting on the man as shown below. The forces are
(i) gravitational force = Mg
(ii) Normal contact force = N

Since the lift is stationary hence the man also appears to be stationary in the frame attached to the ground or even to the lift. Hence we can equate the forces on the man
Hence N = Mg.
Note that the weighing mechine reads the normal force N. Therefore the reading of the weighing mechine is equl to Mg which is the actual weight of the man.
Now consider that the lift is accelerating upward.
Let’s find the reading of the weighing mechine through inertial as well as non inertial frame
In Inertial frame i.e. an observer standing on the ground
We know in inertial frame only actual forces will act on the man.
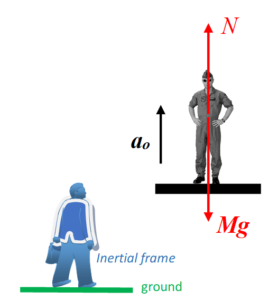
Since for the observer on the ground the lift is going upward with an acceleration \displaystyle {{a}_{o}} therefore he will apply Newton’s second law and make the following equation
\displaystyle N-Mg=M{{a}_{o}}
or \displaystyle N=M(g+{{a}_{o}})
which is the reading of the weighing mechine
Now consider a Non Inertial frame i.e. an observer inside the lift and accelerating with the lift.
In a non inertial frame along with the actual forces there also exists pseudo force which is always opposite to the direction of motion of the frame ( in this case the observer in the lift)
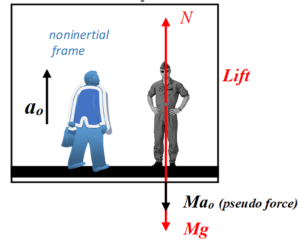
Note that the man on the mechine is now at rest with respect to the observer who is also in the lift hence the observer will make the equation by equating the upward and downward forces on the man
Therefore
\displaystyle N= Mg+M{{a}_{o}}
or
\displaystyle N=M(g+{{a}_{o}}) which is the reading of the weighing mechine.
Point to be noted is that the reading of the weighing mechine comes out to be same irrespective of the frame of reference.
Illustration
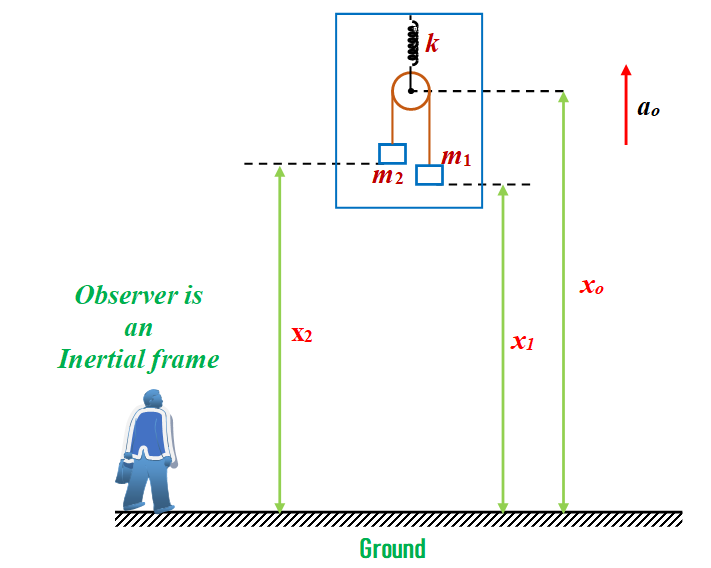
A pulley with two blocks system is attached to the ceiling of a lift moving upward with an acceleration \displaystyle {{a}_{o}}. Find the deformation in the spring as observed by the inertial and non-inertial reference frame observer.
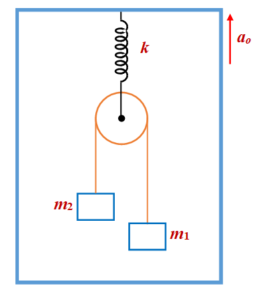
In Inertial Frame
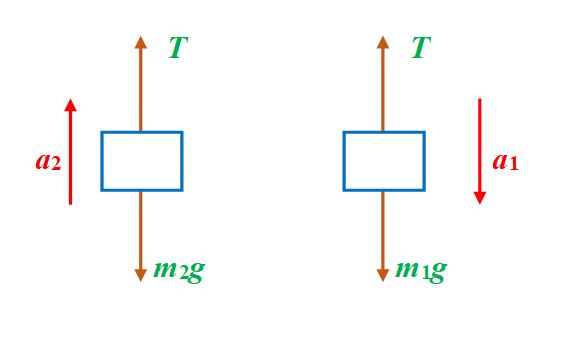
Applying Newton’s Second Law
\displaystyle {{m}_{1}}g-T={{m}_{1}}{{a}_{1}} …..(i)
\displaystyle T-{{m}_{2}}g={{m}_{2}}{{a}_{2}} …(ii)
Constraint relation
\displaystyle ({{x}_{o}}-{{x}_{2}})+({{x}_{o}}-{{x}_{1}})=\text{constant}
or \displaystyle \text{2}{{x}_{o}}-{{x}_{1}}-{{x}_{2}}=\text{constant}
differentiating twice w.r.t. time we get
2 \frac{{{{d}^{2}}{{x}_{0}}}}{{d{{t}^{2}}}}-\frac{{{{d}^{2}}{{x}_{1}}}}{{d{{t}^{2}}}}\,-\,\frac{{{{d}^{2}}{{x}_{2}}}}{{d{{t}^{2}}}}\,=0
or \displaystyle \text{2}{{\text{a}}_{o}}-(-{{a}_{1}})-{{a}_{2}}=0
or \displaystyle {{a}_{2}}=\text{2}{{\text{a}}_{o}}+{{a}_{1}} (iii)
Solving equations (i), (ii) and (iii),
we get T= \left[ {\frac{{2{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right] \displaystyle (g+{{a}_{o}})
Consider F.B.D. of spring
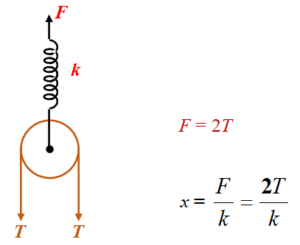
The stretching force on the spring is F = 2T Using Hooke’s law F = kx where x is the deformation in the spring. Thus, x = \frac{F}{k}\,=\left[ {\frac{{4{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right]\,\,\frac{{(g\,+{{a}_{0}})}}{k} |
In Non Inertial Frame
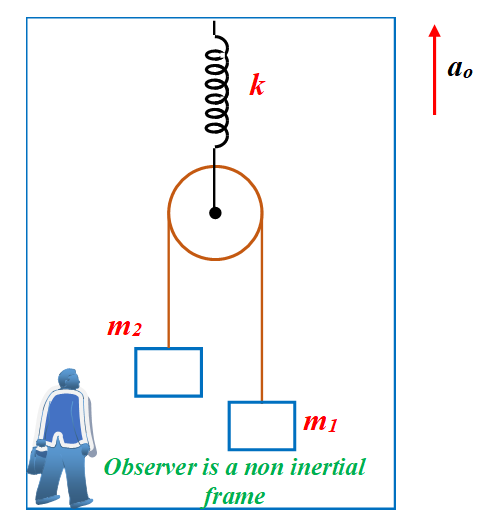
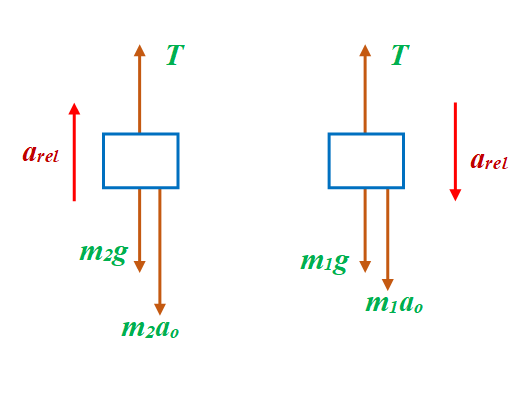
Relative to the centre of the pulley m1 accelerates downward with arel and m2 accelerates upward with arel.
Applying Newton’s Second Law
\displaystyle {{m}_{1}}g+{{m}_{1}}{{a}_{o}}-T={{m}_{1}}{{a}_{{rel}}} …(iv)
\displaystyle -{{m}_{2}}g-{{m}_{2}}{{a}_{o}}+T={{m}_{2}}{{a}_{{rel}}} …. (v)
On adding equations
\displaystyle {{a}_{{rel}}} = \left( {\frac{{{{m}_{1}}\,-\,{{m}_{2}}}}{{{{m}_{1}}\,+{{m}_{2}}}}} \right)\,(g\,+{{a}_{0}})
Substituting arel in equation (iv)
T = \left[ {\frac{{2{{m}_{1}}{{m}_{2}}}}{{{{m}_{{1\,}}}\,+{{m}_{2}}}}} \right]\,(g\,+{{a}_{0}})
Note that tension comes out to be same in both the frames. After this the F.B.D. of the spring is same as that described in inertial frame
Illustration
A pendulum is suspended from the roof of a car that has a constant acceleration a relative to the ground.Find the deflection of the pendulum from the vertical as observed from the ground frame and from the frame attached with the car.
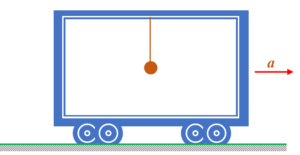
Solution from Inertial Frame
In an inertial frame the suspended bob appears to have an acceleration a along x axis which is caused by the horizontal component of the tension T. But no acceleration is there along y axis. So we apply Newton’s second law along x axis and balance the opposite forces acting along y axis
\displaystyle T\sin \theta =ma ..(i) \displaystyle T\cos \theta =mg ..(ii) From equation (i) and (ii) \displaystyle \tan \theta =\frac{a}{g} or \displaystyle \theta ={{\tan }^{{-1}}}\left( {\frac{a}{g}} \right) |
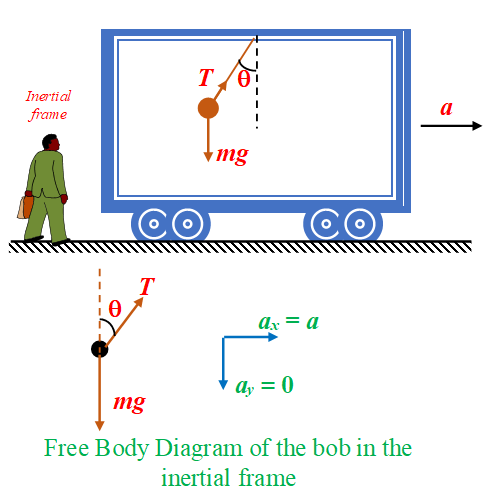
Solution from Non Inertial Frame
In the non-inertial frame of the car, the bob is in static equilibrium under the action of three forces: T, mg and ma. Hence we just equate the opposite forces along x axis and y axis respectively.
\displaystyle T\sin \theta =ma ..(iii)
\displaystyle T\cos \theta =mg ..(iv)
dividing equation (iii) and (iv)
\displaystyle \tan \theta =\frac{a}{g}
or \displaystyle \theta ={{\tan }^{{-1}}}\left( {\frac{a}{g}} \right)
Practice Questions (Basic Level)
1.
Which of the frame is not non inertial
(a) Rotating frame
(b) earth in space
(c) a car in uniform motion
(d) a car in accelerated motion in a straight line
Ans (c)
2.
Read the statements carefully
(i) An inertial frame is always stationary
(ii) A non inertial frame is that which accelerates with respect to an inertial frame
(iii) A frame S1 is moving with acceleration, another frame S2 is moving with same magnitude of acceleration with respect to S1. Then the objects stationary in frame S1 must experience a pseodo force when viewed from S2.
(iv) A man standing in a moving bus falls forward when the brakes are applied is due to some pseudo force.
Now Choose the wrong option
(a) All statements are correct except (i)
(b) Statement (ii) is correct
(c) Statement (iii) is correct
(d) Statement (i) is correct
Ans (d)
3.
An object of mass m is stationary inside a trolley which is accelerating with an acceleration a. A frame S is moving with acceleration \displaystyle {{a}_{o}}. Choose the correct option.
(a) The pseudo force acting on the object with respect to trolley is zero.
(b) The pseudo force acting on the object with respect to frame S is -m \displaystyle {{a}_{o}}
(c) The pseudo force acting on the object with respect to frame S is zero.
(d) The pseudo force acting on the object with respect to frame S is m(a – \displaystyle {{a}_{o}}).
Ans (b)
4.
Choose the correct statement
(a) The centripetal force is a pseudo force
(b) The centripetal and centrifugal force acting on the moon balance each other hence the moon is in dynamic equilibrium
(c) The centrifugal force is a pseudo force
(d) Earth is an inertial frame.
Ans (c)
5.
An observer in a train drops a ball with zero initial velocity. From his perspective the ball appears to fall along a straight line making a fixed angle with the vertical. This implies that
(a) The train is accelerating
(b) The train is retarding
(c) The train is in uniform motion
(d) Both (a) and (b) are correct
Ans (d)
6.
The gravity on the surface of earth is 9.8 \displaystyle m/{{s}^{2}}and at a height of 200km it is about 9.2 \displaystyle m/{{s}^{2}} even then an astronaut in a spaceship orbiting around the earth at a height of 200km feels weightless. It may be due to
(a) small gravity at that height
(b) the centrifugal force due to orbital motion of space ship balance the weight of the astronaut at that height
(c) The weight of the astronaut provides the exact centripetal force required for orbital motion at that height
(d) both (b) and (c) are correct
Ans (d)
7.
A man of mass 40kg is standing on a weighing mechine inside a lift. The weighing mechine reads 80kg this implies that (g=10 \displaystyle m/{{s}^{2}})
(a) The lift is moving downward with an acceleration of 10 \displaystyle m/{{s}^{2}}
(b) The lift is going down with a retardation of 10 \displaystyle m/{{s}^{2}}
(c) The lift is going up with an acceleration of 10 \displaystyle m/{{s}^{2}}
(d) Both (b) and (c) are correct
Ans (d)
Practice Questions (JEE Main Level)
1.
A block of mass M has a mass m in contact with it as shown in figure. The coefficient of friction between the block and the mass is µ. What is the minimum acceleration of the block so that the mass m does not fall? Assuming no friction between the block and the ground
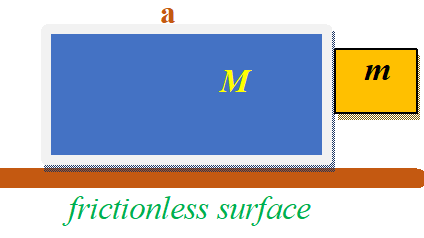
(a) \displaystyle \mu g
(b) \displaystyle \frac{g}{\mu }
(c) \displaystyle \frac{\mu }{g}
(d) \displaystyle \frac{{M\mu g}}{m}
Ans (b)
2.
In the arrangement shown in the figure, the block of mass m and the wedge of mass M always remain in contact. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the block relative to the wedge and with respect to ground.
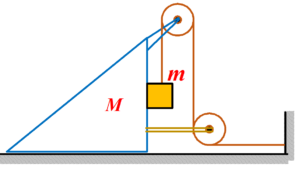
(a)\frac{{mg}}{{2m\,+M}};\frac{{mg\sqrt{2}}}{{2m\,+\,M}}
(b)\frac{{mg}}{{m\,+M}};\frac{{mg\sqrt{2}}}{{2m\,+\,M}}
(c)\frac{{mg}}{{m\,+2M}};\frac{{mg\sqrt{2}}}{{m\,+\,2M}}
(d)\frac{{mg}}{{m\,+M}};\frac{{mg\sqrt{2}}}{{2m\,+\,M}}
Ans (a)
3.
For the arrangement shown in the figure, find the magnitude of the horizontal acceleration a to keep the blocks m1 and m2 stationary with respect to the large block. Assume all surfaces to be frictionless.
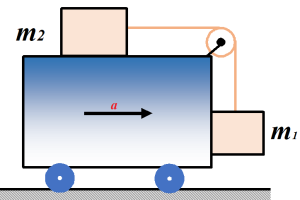
(a)\left( {\frac{{{{m}_{1}}}}{{{{m}_{2}}-{{m}_{1}}}}} \right)\,g
(b)\left( {\frac{{{{m}_{1}}}}{{{{m}_{2}}}}} \right)\,g
(c)\left( {\frac{{{{m}_{1}}+{{m}_{1}}}}{{{{m}_{2}}}}} \right)\,g
(d)\left( {\frac{{{{m}_{2}}}}{{{{m}_{1}}}}} \right)\,g
Ans (b)
4.
Find the magnitude of the horizontal force F required to keep the block stationary with respect to wedge. Assume all the surfaces to be frictionless.
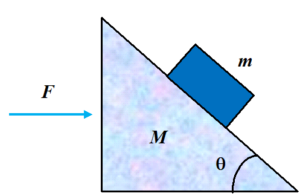
(a) (M + m) g tan \displaystyle \theta
(b) (M – 2m) g tan \displaystyle \theta
(c) (M x m) g tan \displaystyle \theta
(d) (2M + m) g tan \displaystyle \theta
Ans (a)
5.
A solid sphere of mass 2 kg is resting inside a cube as shown in the figure. The cube is moving with a velocity \vec{v}=\left( {5t\,\,\hat{i}+2t\,\,\,\hat{j}} \right)m/s. Here t is the time in second. All surfaces are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube.
(Take g = 10 m/s2)
(a) \sqrt{{29}} N
(b) 29 N
(c) 26 N
(d) \sqrt{{89}} N
Ans (c)
Practice Questions (JEE Advance Level)
1.
Three blocks are placed over one another as shown in the diagram. Assuming ground is smooth and the coefficient of friction between the smaller blocks and the bigger block is \mu . What maximum force F must be applied on block M3 so that M1 and M2 remains at rest with respect to M3?
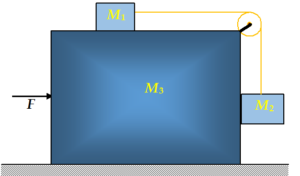
(a)\displaystyle {{F}_{{\max }}}=\left[ {\frac{{\left( {{{M}_{1}}-{{M}_{2}}+{{M}_{3}}} \right){{M}_{2}}}}{{{{M}_{1}}}}} \right]g
(b) \displaystyle {{F}_{{\max }}}=\frac{{({{M}_{1}}+{{M}_{2}}+{{M}_{3}})\mu g({{M}_{1}}+{{M}_{2}})}}{{({{M}_{1}}-\mu {{M}_{2}})}}
(c) \displaystyle {{F}_{{\max }}}=\frac{{({{M}_{1}}+{{M}_{2}}+{{M}_{3}})g({{M}_{1}}+\mu {{M}_{2}})}}{{({{M}_{1}}-\mu {{M}_{2}})}}
(d)\displaystyle {{F}_{{\max }}}=\left[ {\frac{{\left( {{{M}_{1}}-\mu{{M}_{2}}-{{M}_{3}}} \right){{M}_{2}}}}{{{{M}_{1}}}}} \right]g
Ans (b)
2.
In the figure, a block of mass m = 0.5 kg is on a wedge of mass M = 2 kg. The wedge is subjected to a horizontal force \displaystyle {{F}_{o}} and slides on a frictionless surface. The coefficient of static friction between block and wedge is 0.6. Find the range of values of \displaystyle {{F}_{o}} for which the block does not slide on the incline. Take \displaystyle \theta = 37°
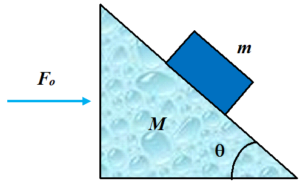
(a)Fmin= 5 N, Fmax= 80.25 N
(b)Fmin= 2.5 N, Fmax= 62.36 N
(c)Fmin= 1.35 N, Fmax= 23.68 N
(d)Fmin= 2.0 N, Fmax= 60.45 N
Ans (b)
3.
A 4 kg block rests on top of a 5 kg block, which rests on a frictionless table. The coefficient of friction between the two blocks is such that the upper block starts to slip when the horizontal force F applied to the lower block is 27 N. Suppose that a horizontal force is now applied only to the upper block. What is its maximum value for the blocks to slide without slipping relative to each other ?
(a) 21.6 N
(b) 20.0 N
(c) 25.5 N
(d) 30.0 N
Ans (a)
4.
Figure shows a small block of mass m kept at the left end of a larger block of mass M and length l. The system can slide on a horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is µ and that between the blocks is µ/2. Find the time elapsed before the smaller block separates from the bigger block.
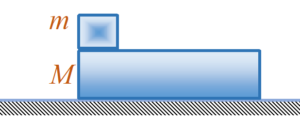
(a)\sqrt{{\frac{{3M\ell }}{{(M\,m)\mu g}}}}
(b)\sqrt{{\frac{{4M\ell }}{{(M\,+m)\mu g}}}}
(c)\sqrt{{\frac{{M\ell }}{{(M\,+m)\mu g}}}}
(d)\sqrt{{\frac{{M\ell }}{{(M\,-m)\mu g}}}}
Ans (b)
5.
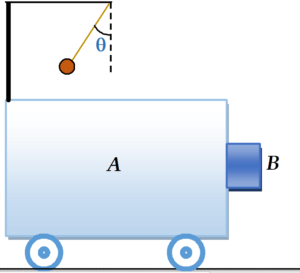
A trolley A has a simple pendulum suspended from a stand fixed to its deck. A block B is in contact with its vertical wall. The trolley is accelerated to the right such that the block just does not fall down. Calculate the inclination \displaystyle \theta of the pendulum thread to the vertical. The coefficient of friction between the block and trolley is µ = 0.5.
(a) \displaystyle {{\tan }^{{-1}}}(1)
(b) \displaystyle {{\tan }^{{-1}}}(2)
(c) \displaystyle {{\tan }^{{-1}}}(3)
(d) \displaystyle {{\tan }^{{-1}}}(4)
Ans (b)
Question (6 and 7)
A massless rod of length l with a small load of mass m at the end is freely pivoted at point A. The rod is initially in a vertical position and is touching a block of mass M which rests on a smooth horizontal ground. The rod is given a slight jerk and it starts rotating about point A. This causes the block to move forward.

After some time the rod forms an angle a with the horizontal. at this instant the speed of the mass m is v and the magnitude of its tangential acceleration is at.
6.
Determine the velocity and acceleration of mass M
(a) v\sin \alpha ;{{a}_{t}}\sin \alpha -\frac{{{{v}^{2}}}}{3}\cos \alpha
(b) v\sin \alpha ;{{a}_{t}}\sin \alpha -\frac{{{{v}^{2}}}}{2}\cos \alpha
(c) v\sin \alpha ;{{a}_{t}}\sin \alpha -\frac{{{{v}^{7}}}}{9}\cos \alpha
(d) v\sin \alpha ;{{a}_{t}}\sin \alpha -\frac{{{{v}^{3}}}}{6}\cos \alpha
Ans(b)
7.
Now when a = 30o the normal force between m and M vanishes.
(i) Find the velocity of mass M at this instant.
(a)\frac{1}{2}\sqrt{{\frac{{gl}}{2}}}
(b)\frac{3}{5}\sqrt{{\frac{{gl}}{2}}}
(c)\frac{1}{9}\sqrt{{\frac{{gl}}{9}}}
(d)\frac{5}{9}\sqrt{{\frac{{gl}}{3}}}
Ans (a)
(ii) Find the value of (M/m) so that this happens
(a)6
(b)4
(c)0
(d)1
Ans(b)
8.
A 40 kg block is moving to the right with a speed of 1.5 m/s when it is acted upon by the forces F1 and F2. These forces vary with time in the manner as shown in the graphs. Find the velocity of the block after t = 6 s. There is no friction anywhere and all the pulleys and string are ideal.
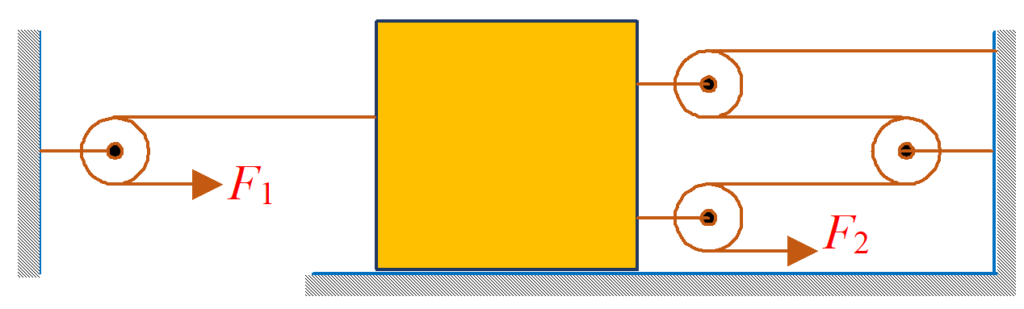
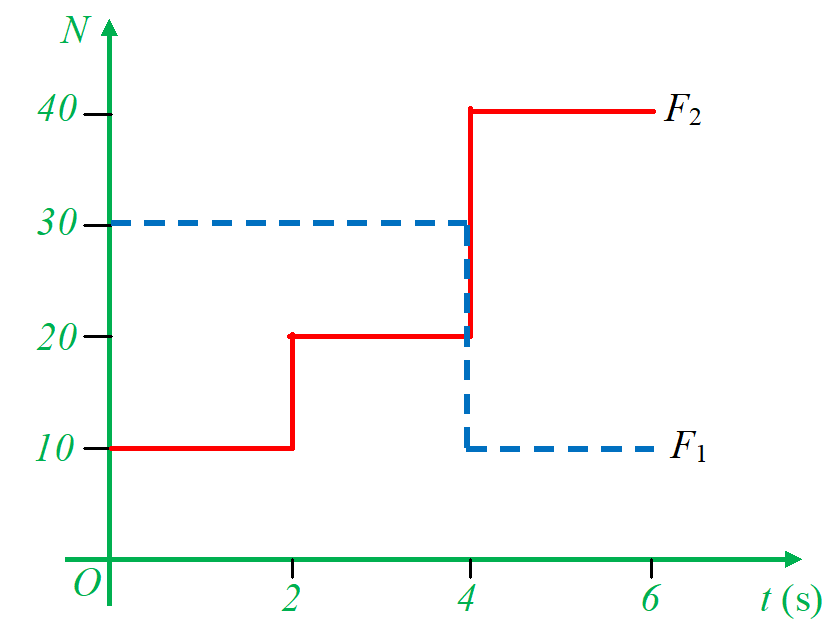
(a) 5 m/s
(b) 3 m/s
(c) 9 m/s
(d) 12 m/s
Ans (d)
9.
A 20 kg block B is suspended from an ideal string attached to a 40 kg block A. The acceleration of the block B shown in figure immediately after the system is released from rest is \frac{{ng}}{{2\sqrt{2}}}. Where n is. (Neglect friction)
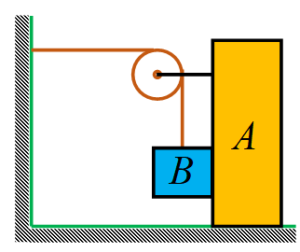
(a) 1
(b) 2
(c) 3
(d) 4
Ans (a)
10.
A heavy spherical ball is constrained in a frame as shown in figure. The inclined surface is smooth. The maximum acceleration with which the frame can move without causing the ball to leave the frame is \frac{n}{{\sqrt{3}}}.The value of n must be
(a) 3
(b) 5
(c)10
(d) 7
Ans (c)