Video Lecture
Theory For Notes Making
Compound Pendulum
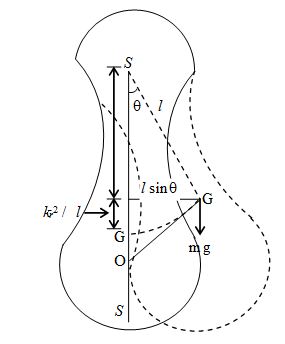
A compound pendulum is a rigid body capable of oscillating freely about a horizontal axis passing through it (figure). At equilibrium position, the centre of gravity G lies vertically below the suspension position S. Let the distance SG be l. If the pendulum is given a small angular displacement q at any instant, it oscillates over the same path. Is its motion simple harmonic? To answer this question we note that the restoring torque about Sis mg l sinq and it tends to bring the pendulum towards the equilibrium position.
If I is the moment of inertia of the body about the horizontal axis passing through S, the restoring torque equals Id2q / dt2. Hence, the equation of motion can be written as
\displaystyle I\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}=-mgl\sin \theta
For small angular displacement, \displaystyle \sin \theta \simeq \theta , above equation takes the form
\displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}+\frac{{mgl}}{I}\theta =0 …(i)
This equation shows that a compound pendulum executes SHM and the time period is given by
\displaystyle T=\frac{{2\pi }}{\omega }=2\pi \sqrt{{I/mgl}}
According to theorem of parallel axes, the moment of inertia I of a body about any axis and its inertia Icm about a parallel axis passing through its centre of gravity are connected by the relation
I = Icm+ml2 …(ii)
Where l is the distance between the two axis and Icm = \displaystyle mk_{r}^{2}.The quantity kr is the radius of gyration of the body about the axis passing through G.
On substituting the expression for I from equation (ii) in equation (i), we obtain
\displaystyle T=2\pi \sqrt{{\frac{{k_{r}^{2}+{{l}^{2}}}}{{gl}}}} …(iii)
On comparing the expression for T with that by time period for a simple pendulum, you will note that two periods become equal if l in equation (iii) is replaced by \displaystyle L=\sqrt{{(k_{r}^{2}/l)}}+l.This is called the length of an equivalent simple pendulum. If we produce the line SG and take a point O on it such that \displaystyle SO=\frac{{k_{r}^{2}}}{l}+l,then O is called the centre of oscillation.
Torsional Systems
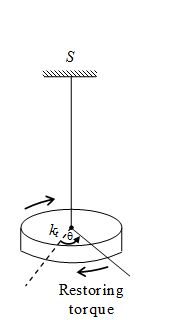
If one end of a long thin wire is clamped to a right support and the other end is fixed to the centre of a massive body such as a disc, cylinder, sphere or rod, then the arrangement is called a torsional pendulum. You will come across many instruments in your physics laboratory which execute torsional oscillations. The most familiar of these is the inertia table. It is commonly used to determine the moment of inertia of regular as well as irregular bodies. Ammeters, voltmeters and moving coil galvanometers are other measuring devices where restoring torque is provided by spiral springs or suspension fibres.
When a torsional system is twisted and then left free, it executes torsional oscillations in a horizontal plane. For an angular displacement q, the restoring torque is –ktq. Here kt is a constant which depends on the properties of the wire.
If I is the moment of inertia of the system about the axis of rotation and d2q/dt2 is the angular acceleration, then according to the equation of motion Ia = t we get
\displaystyle I\frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}=-{{k}_{t}}\theta
Comparing this equation with standard equation of SHM
\displaystyle \frac{{{{d}^{2}}\theta }}{{d{{t}^{2}}}}=-\omega _{0}^{2}\theta , …(i)
we conclude that
\displaystyle w=\sqrt{{{{k}_{t}}/I}}.
Hence \displaystyle T=2\pi \sqrt{{I/{{k}_{t}}}} …(ii)
\displaystyle K.E.=\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}-\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}\cos 2\omega t
Energy Of an Oscillator in SHM (Transformation of Energy in Oscillating system)
Consider the spring-mass system shown in figure. When the mass is pulled, the spring is elongated. The amount of energy required to elongate the spring through a distance dx is equal to the work done in bringing about this change. It is given by dW = dU = Fdx, where F is the applied force (such as by hand). This force is balanced by the restoring force. That is, its magnitude is same as that of F and we can write F = kx. Therefore, the energy required to elongate the spring through a distance x is
\displaystyle U=\int\limits_{0}^{x}{{F\,dx}}=k\int\limits_{0}^{x}{{xdx}}=\frac{1}{2}k{{x}^{2}} … (i)
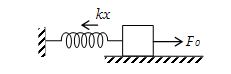
This energy is stored in the spring in the form of potential energy and is responsible for oscillations of the spring-mass system.
On substituting for the displacement \displaystyle x=a\sin \left( {\omega t+\phi } \right)
\displaystyle U=\frac{1}{2}k{{a}^{2}}{{\sin }^{2}}(\omega t+\phi ) … (ii)
Note that at t = 0, the potential energy is zero if f = 0 i.e. the body starts from mean position. Equation shows that potential energy of body is maximum at extreme position i.e. x = ± a and is equal to \displaystyle \frac{1}{2}k{{a}^{2}}
\displaystyle {{U}_{0}}=\frac{1}{2}k{{a}^{2}}{{\cos }^{2}}\phi … (iii)
As the mass moves towards the equilibrium position from the extreme position the potential energy starts changing into kinetic energy (K.E.). The kinetic energy at any time t is given by
K.E. = \displaystyle \frac{1}{2}mv2.
where \displaystyle v=\frac{{dx}}{{dt}}=a\omega \cos (\omega t+\phi )
K.E. = \displaystyle \frac{1}{2}m\omega _{{}}^{2}{{a}^{2}}{{\cos }^{2}}(\omega t+\phi )= \displaystyle \frac{1}{2}k{{a}^{2}}{{\cos }^{2}}(\omega t+\phi ) … (iv)
Since \displaystyle \omega _{{}}^{2}=k/m.
One can also express K.E. in terms of the displacement by writing
K.E. = \displaystyle \frac{1}{2}k{{a}^{2}}[1-{{\sin }^{2}}(\omega t+\phi )] … (v)
= \displaystyle \frac{1}{2}k{{a}^{2}}-\frac{1}{2}k{{a}^{2}}{{\sin }^{2}}(\omega t+\phi )
= \displaystyle \frac{1}{2}k{{a}^{2}}-\frac{1}{2}k{{x}^{2}}=\frac{1}{2}k({{a}^{2}}-{{x}^{2}}) … (vi)
This shows that when an oscillating body passes through the equilibrium position (x = 0), its kinetic energy is maximum and equal to \displaystyle \frac{1}{2}k{{a}^{2}}.
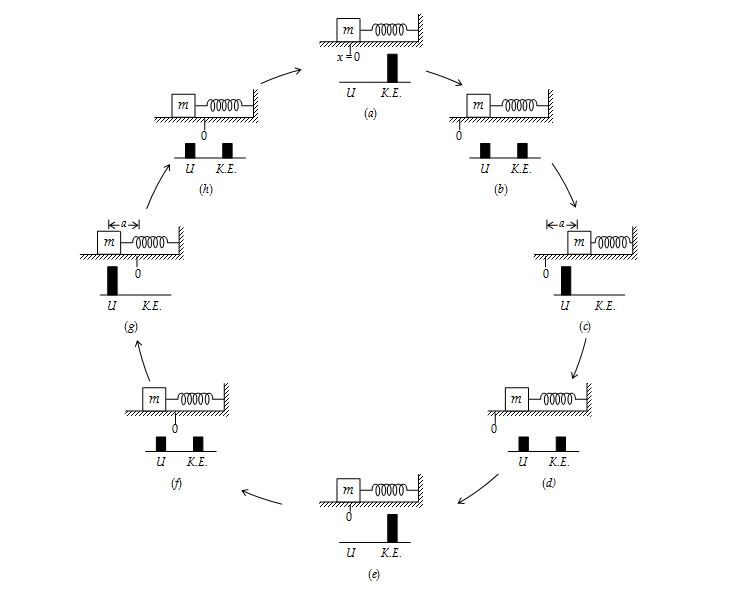
It is thus from the explicit time dependence of equations of kinetic energy and potential energy that in a spring-mass system or any oscillator the total energy of system alternately becomes kinetic and potential energy. Let us consider that the initial phase f = 0. At t = 0, kinetic energy stored in the body is maximum and potential energy of the spring is zero. At t = T /4, when the body is at extreme position the kinetic energy is zero and potential energy is maximum. As the body oscillates, energy oscillates from kinetic form to potential form and vice versa. At any instant, the total energy, E, of the oscillator will be sum of both these energies. Hence, from equation of kinetic energy and potential energy, we can write
\displaystyle E=U+K.E.=\frac{1}{2}k{{a}^{2}}{{\sin }^{2}}(\omega t+\phi )+\frac{1}{2}k{{a}^{2}}{{\cos }^{2}}(\omega t+\phi )=\frac{1}{2}k{{a}^{2}}
This means that the total energy remains constant independent of time and is proportional to the square of the amplitude. As long as there are no dissipative force like friction, the total mechanical energy will be conserved.
The plots of U and K.E. as a function of x as obtained from equation (i) and (vi) are shown in figure.
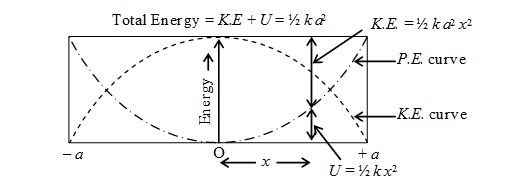
You will note that (i) the shape of these curves is parabolic, (ii) the shape is symmetric about the origin, and (iii) the potential and kinetic energy curves are inverted with respect to one another. This is due to phase difference of p/2 between the displacement and the velocity of harmonic oscillator. For any value of x, the total energy is the sum of kinetic energy and potential energies and is equal to ½ka2. This is represented by the horizontal line.
The points where this horizontal line intersect the potential energy curve are called the ‘turning points’. The oscillating particle cannot be beyond these and turns back towards the equilibrium position. At these points, the total energy of the oscillator is entirely potential (E = U = ½ka2) and K.E is zero. At the equilibrium position (x = 0) the energy is entirely kinetic (K.E. = E = ½ka2).
At any intermediate position energy is partly kinetic and partly potential, but the total energy always remains the same. The transformation of energy in a spring-mass system is shown in figure.
Illustration
A particle executing simple harmonic motion with frequency v. Then calculate the frequency corresponding to its kinetic energy.
\displaystyle K.E.=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}{{\sin }^{2}}\omega t
\displaystyle =\frac{1}{2}\times \frac{1}{2}m{{\omega }^{2}}{{a}^{2}}\left[ {2{{{\sin }}^{2}}\omega t} \right]
\displaystyle =\frac{1}{2}\times \frac{1}{2}m{{\omega }^{2}}{{a}^{2}}\left[ {1-\cos 2\omega t} \right]
\displaystyle \left\{ {\cos 2\omega t=1-2{{{\sin }}^{2}}\omega t} \right\}
\displaystyle K.E.=\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}-\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}\cos 2\omega t
Objective Assignment
Q.1.
The potential energy of a particle executing SHM varies sinusoidally with frequency \displaystyle f. The frequency of oscillation of the particle will be
(a) \displaystyle \frac{f}{2}
(b) \displaystyle \frac{f}{{\sqrt{2}}}
(c) \displaystyle f
(d) \displaystyle 2f
Ans. (a)
Q.2
The amplitude of a particle executing SHM about O is 10 cm. Then
(a) When the KE is 0.64 times of its maximum KE, its displacement is 6 cm
from O
(b) its speed is half of maximum speed when its displacement is half the maximum displacement
(c) Both (a) and (b) are correct
(d) Both (a) and (b) are wrong
Ans. (a)
Q.3
The KE and PE of a particle executing SHM with amplitude A will be equal when its displacement is:
(a) \displaystyle \frac{{f\mu \mu \prime }}{{\mu \mu \prime }}
(b) \displaystyle {{\sin }^{{1}}}\left( {\frac{5}{7}} \right)
(c) \displaystyle {{\sin }^{{1}}}\left( {\sqrt{{\frac{9}{8}}}} \right)
(d) \displaystyle {{\sin }^{{1}}}\left( {\frac{1}{2}} \right)
Ans. (c)
Q.4
A linear harmonic oscillator of force constant 2´106 N/m and amplitude 0.01m ha a total mechanical energy of 160 J. Its
(a) maximum potential energy is 160 J
(b) maximum potential energy is 100 J
(c) maximum potential energy is zero
(d) minimum potential energy is 100 J
Ans. (a)
Q.5
The potential energy of a simple harmonic oscillator when the particle is half way to its end point is
(a) \displaystyle \frac{1}{4}E
(b) \displaystyle \frac{1}{2}E
(c) \displaystyle \frac{2}{3}E
(d) \displaystyle \frac{1}{8}E
Ans. (a)
Q.6
Identify the correct variation of potential energy U as a function of displacement x from mean position of a harmonic oscillator (U at mean position = 0)
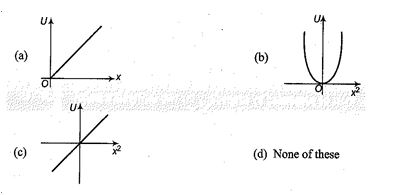
Ans. (c)
Q.7
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
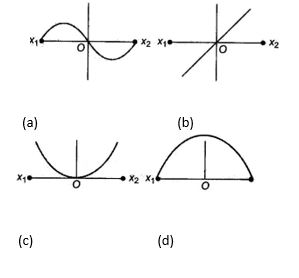
Ans. (c)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
