Video Lecture
Theory For Making Notes
DOPPLER EFFECT
When a source and observer (listener/ Detector) of sound separated by a large distance are stationary then the detector (usually listener) receives the same number of waves per second as that emitted by the source. So the frequency heard by the observer is equal to the frequency emitted by the source.
However, if there is motion of source and/or observer relative to the medium(usually air) along the line joining the source to the detector, the number of waves received per second in usually different from that emitted by the source and therefore the frequency or pitch of the source appear to be different to the observer.
This apparent charge in frequency or pitch due to motion of source and detector relative to the medium along their line of sight is called Doppler-effect.
The most general expression for the Doppler effect can be written as,
\displaystyle f’={{f}_{{}}}\left( {\frac{{C\pm {{V}_{o}}\pm {{V}_{w}}}}{{C\pm {{V}_{S}}\pm {{V}_{w}}}}} \right) (See the video lectures for its detailed derivation)
f’= apparent frequency heard by observer
where f= actual frequency emitted by the source
C= speed of sound
{{V}_{o}}= speed of observer
{{V}_{S}}= speed of source
Vw = speed of wind or medium
We shall analyse changes in frequency under three different situations.
(A) Source alone in motion
(B) Detector alone in motion
(C) Source and detector both in motion.
Important points
(I)
Whenever the source moves towards the observer or observer moves towards the source the apparent frequency tends to increase whereas If they move away from each other the apparent frequency tends to decrease. So while using the above expression choose +ve or –ve sign of velocities accordingly.
(II)
Always take the velocity of sound from source to observer
(III)
If the wind blows in the direction of sound take its velocity as +ve, and if the wind blows against the sound take its velocity as –ve.
(IV)
In all the cases discussed below the velocity of the wind or medium is taken as zero.
(Case -1)
Source is moving towards a stationary observer so Vo = 0.
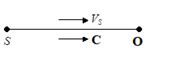
Hence f’=f\left[ {\frac{{C\pm 0}}{{C\pm \,{{V}_{S}}}}} \right]\,\,\,=f\left[ {\frac{C}{{C\pm {{V}_{S}}}}} \right]
Now As the source is moving toward the observer so apparent frequency increases which is possible only if the denominator on RHS should decrease therefore choose –ve sign before the source velocity Vs.
f’=f\left[ {\frac{C}{{C-{{V}_{S}}}}} \right]
i.e., apparent frequency or pitch will increase (f’>f).
(Case -2)
Source moves away from thestationary observer so Vo = 0.
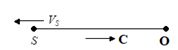
Now As the source is moving away from the observer so apparent frequency decreases which is possible only if the denominator on RHS should increase therefore choose +ve sign before the source velocity Vs.
f’={{f}_{{}}}\left[ {\frac{{C-0}}{{C+{{V}_{S}})}}} \right]\,\,=\,\,{{f}_{{}}}\left[ {\frac{C}{{C+{{V}_{S}}}}} \right]
i.e., apparent frequency or pitch will decrease (f'<{{f}_{{}}})
(Case -3)
Observer is moving away from the stationary source so {{V}_{S}}=0
Now As the observer is moving away from the source so apparent frequency decreases which is possible only if the numerator on RHS should decrease therefore choose -ve sign before the observer velocity Vo.
f’=f\left[ {\frac{{C-{{V}_{o}})}}{{C-0}}} \right]={{f}_{{}}}\left[ {\frac{{C-{{V}_{o}}}}{C}} \right]
i.e., apparent frequency or pitch decreases (f'<f).
(Case -4)
Detector is moving towards a stationary source
Now As the observer is moving towards the source so apparent frequency increases which is possible only if the numerator on RHS should increase therefore choose +ve sign before the observer velocity Vo
f’={{f}_{{}}}\left[ {\frac{{C+{{V}_{o}}}}{{C\pm 0}}} \right]=f\left[ {\frac{{C+{{V}_{o}}}}{C}} \right]
i.e., apparent frequency or pitch increases (f’>f).
(Case -5)
Source and detector both move towards each other.( It’s a combination of case-1 and case-4 )
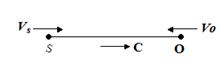
Now As the source is moving toward the observer so apparent frequency increases which is possible only if the denominator on RHS should decrease therefore choose –ve sign before the source velocity Vs. However as the observer is moving towards the source so apparent frequency increases which is possible only if the numerator on RHS should increase therefore choose +ve sign before the observer velocity Vo
\displaystyle f’=f\left[ {\frac{{C\pm {{V}_{o}})}}{{C\pm {{V}_{S}})}}} \right]={{f}_{{}}}\left[ {\frac{{C+{{V}_{o}}}}{{C-{{V}_{S}}}}} \right]
Which shows maximum increase in frequency or pitch.
(Case -6)
Source and detector both move away from each other. ( It’s a combination of case-2 and case-3 )
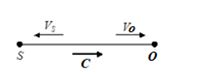
Using the above concept we can choose the signs easily
\displaystyle f’=f\left[ {\frac{{C\pm {{V}_{o}})}}{{C\pm {{V}_{S}})}}} \right]={{f}_{{}}}\left[ {\frac{{C-{{V}_{o}}}}{{C+{{V}_{S}}}}} \right]
Which shown maximum decrease in frequency or pitch.
(Case -7)
Source is chasing the observer
Using the same concept we can choose the signs easily
\displaystyle f’=f\left[ {\frac{{C\pm {{V}_{o}})}}{{C\pm {{V}_{S}})}}} \right]={{f}_{{}}}\left[ {\frac{{C-{{V}_{o}}}}{{C-{{V}_{S}}}}} \right]
(Case -8)
Observer is chasing the source
Using the same concept we can choose the signs easily
\displaystyle f’=f\left[ {\frac{{C\pm {{V}_{o}})}}{{C\pm {{V}_{S}})}}} \right]={{f}_{{}}}\left[ {\frac{{C-{{V}_{o}}}}{{C-{{V}_{S}}}}} \right]
Important Cases and Facts:
1.
The change in frequency or pitch depends on speeds of source and detector and not on distance between them. But intensity, I\,\,\,\propto \,\,\frac{1}{{{{r}^{2}}}}, (r= distance).
2.
If the motion is along some other direction, the components of velocities along the line joining source and detector are considered in equation …(i).
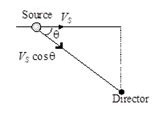
Then, {{V}_{S}}\to {{V}_{S}}\cos \theta \, [from figure]
f’={{f}_{{}}}\left[ {\frac{C}{{C-{{V}_{S}}\cos \theta }}} \right] (where, {{V}_{D}}=0)
In such situations, f‘ is not constant and depends on \theta .
4.
If one is at center of a circle while the other is moving on the circumference then apparent frequency remains equal to the actual frequency.
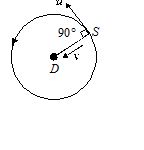
For example if the observer is at the center and the source is moving on the circle then
{{V}_{o}}=0
{{V}_{S}}=u\cos 90{}^\circ =0
f’=f\left[ {\frac{{C\pm 0}}{{C\pm 0}}} \right]={{f}_{{}}}
(no change in frequency)
where, source moving with speed u.
5.
If source and detector both move in same direction with same speed. {{V}_{D}}={{V}_{S}}=u
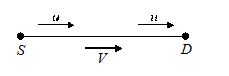
f={{f}_{o}}\left[ {\frac{{V-u}}{{V-u}}} \right]={{f}_{o}} (no charge in frequency)
Beats heard due to Doppler’s effect
In case of reflection of sound from a reflector. The observer `O’ will receive two notes, one directly from the source `S’of frequency f1and other f2from the reflector (which also act as a source of reflected sound).
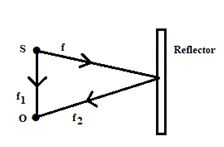
If the two frequencies are slightly different the superposition of there waves will produce beats and beat frequency can be used to determine the speed of the reflector (source).
Take care that f1 and f2 may be equal to f if all are at rest so no beat is produced
When the reflector is moving towards stationary source then we solve the question in two steps
If the source is at rest and a reflector is moving towards the source with speed u, consider the reflector as an observer who will hear the frequency ({{f}_{1}}) { case-4 discussed above}
{{f}_{1}}=f\left[ {\frac{{C+u}}{C}} \right]\,\,\,\,\,\,\,\,={{f}_{{}}}\left[ {1+\frac{u}{C}} \right]
Now, consider the reflector as a source of actual frequency f1 moving toward the observer standing near source .{case –1 discussed above}. So, the frequency received by the observer O from the reflector is f2 which is given below
{{f}_{2}}={{f}_{1}}\left[ {\frac{C}{{C-u}}} \right]\,\,\,\,={{f}_{{}}}\left[ {\frac{{C+u}}{C}} \right]\,\,\,\left[ {\frac{C}{{C-u}}} \right]
hence {{f}_{2}}={{f}_{{}}}\left[ {\frac{{C+u}}{{C-u}}} \right]\,
Special Case:
If u<<C, {{f}_{2}}={{f}_{{}}}\left[ {1+\frac{u}{C}} \right]\,\,{{\left[ {1-\frac{u}{C}} \right]}^{{-1}}}={{f}_{{}}}\left[ {1+\frac{u}{C}} \right]\,\,{{\left[ {1+\frac{u}{C}} \right]}^{{}}}={{f}_{{}}}{{\left[ {1+\frac{u}{C}} \right]}^{2}}
hence {{f}_{2}}=f\left[ {1+\frac{{2u}}{C}} \right]
Therefore, beat frequency is ={{f}_{2}}-f=f\left[ {\frac{{2u}}{C}} \right]
7.
When speed of detector or source becomes equal to or greater than sound. Doppler formula (i) does not apply.
Illustration
A source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, ‘A’ away from the wall and B towards the wall and C inside the source. Velocity of sound in air is 330 m/s
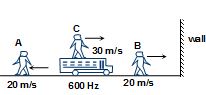
(a) Find the frequency of direct sound observed by observer A.
(b) Find the frequency of reflected sound observed by observer B.
(c) Frequency of directed sound observer by observer C.
Solution:
(a) Use Case-6 .Frequency of direct sound observed by observer A is
\displaystyle f’={{f}_{{}}}\left[ {\frac{{C-{{V}_{o}}}}{{C+{{V}_{S}}}}} \right]
=600\left( {\frac{{330-20}}{{330+30}}} \right)=600\frac{{310}}{{360}}Hz
(b)
Reflected frequency from the wall is
fwall = 600\left\{ {\frac{{330}}{{330-30}}} \right\}=600\frac{{330}}{{300}}
then frequency observed by observer B is
f = fwall \left\{ {\frac{{330+20}}{{330}}} \right\}=600\frac{{330}}{{300}}\cdot \frac{{350}}{{330}} = 600\cdot \frac{{350}}{{300}}
(c)
Frequency of direct sound observer by observer C is 600 Hz.
Illustration
A train is moving with a constant speed along a circular track. The engine of the train emits a sound of frequency f. then find the frequency heard by the guard at rear end of the train.
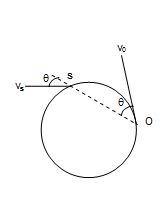
Solution:
Let C be the speed of sound and u the speed of train.
Then vs = v0 = u
and f¢ = f \displaystyle \left( {\frac{{C+{{v}_{0}}\cos \theta }}{{C+{{v}_{s}}\cos \theta }}} \right)
= f \displaystyle \left( {\frac{{C+u\cos \theta }}{{C+u\cos \theta }}} \right) = f
Illustration
A band playing music at a frequency f is moving towards a wall at a speed vb. A motorist is following the band with a speed vm. If v is the speed of sound, obtain an expression for the beat frequency heard by the motorist.
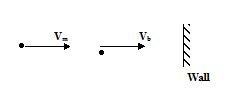
Required beat frequency = |f1 – f2|
Where, f1 = apparent frequency for the motorist corresponding to the signals directly coming to him from source, and f2 = apparent frequency for the motorist corresponding to the signals coming to him after reflection.
Now, f1 = f\left[ {\frac{{V+{{V}_{m}}}}{{V+{{V}_{b}}}}} \right] & f2 = f¢ \displaystyle \frac{{V+{{V}_{m}}}}{V}
Where f ¢ is the frequency at which signals from sources are incident on wall.
f ¢ = f \left[ {\frac{V}{{V-{{V}_{b}}}}} \right]
f2 = f \left[ {\frac{V}{{V-{{V}_{b}}}}} \right]\left[ {\frac{{V+{{V}_{m}}}}{V}} \right]=f\left[ {\frac{{V+{{V}_{m}}}}{{V-{{V}_{b}}}}} \right]
Hence , the beat frequency = |f1 – f2| = \frac{{2{{V}_{b}}\left( {V+{{V}_{m}}} \right)f}}{{\left( {{{V}^{2}}-V_{b}^{2}} \right)}}.
Illustration
A man standing near a railway track hears the whistle of an engine, which is approaching him with a velocity of 36 km/h. What is the actual frequency of the whistle, if the apparent pitch of the whistle as heard by the man is 800 Hz? Velocity of sound is 350 m/s.
Solution:
Using the formula of case-1 discussed above for most general case, \displaystyle f\prime \,=\,f\,\left( {\frac{C}{{C-{{V}_{s}}}}} \right)
here we have, C = 350 m/s, vs = 36 km/h = 10 m/s, and f ¢ = 800 Hz
800 = f \left( {\frac{{350}}{{350\,-\,10}}} \right)
or f = \frac{{800\,\times \,(350-10)}}{{350}}\, = 777.14 Hz
Illustration
The difference between the apparent frequency of a source of sound as perceived by an observer during its approach and its recession is 2% of the natural frequency of the source. If the velocity of sound in air is V= 300 m/s, Find the velocity of the source .
Solution:
The apparent frequency during approach is
\displaystyle {{f}_{a}}\ \,\,\,=\,\ {{f}_{0}}\ \left( {\frac{V}{{V\ -\ {{V}_{a}}}}} \right)\ \,\,\,\,=\,\ {{f}_{0}}\ \left( {\frac{{300}}{{300\ -\ {{V}_{a}}}}} \right)
The apparent frequency during recession is
{{f}_{r}}\ \,\,\,=\,\ {{f}_{0}}\ \left( {\frac{V}{{V\ \,+\,\ {{V}_{r}}}}} \right)\ \,\,\,\,\,=\ \,{{f}_{0}}\ \left( {\frac{{300}}{{300\ +\,\ {{V}_{r}}}}} \right)
Hence ({{f}_{a}}\ -\,\ {{f}_{r}})\ \left( {\frac{2}{{100}}} \right)\ \,{{f}_{0}}\ \,\,\,\,\,\,=\,{{f}_{0}}\ \left[ {\frac{{300}}{{300\ -\ V}}\ \,-\ \,\frac{{300}}{{300\ +\ V}}} \right],
\ {{V}_{a}}\ =\ \,\,{{V}_{r}}= V = velocity of source
or 2[(300)2 – V2] = 3 [2V] ´ 104
or V2 + 3 ´ 104V – (300)2 = 0
Omitting V2, as small quantity,
V\ \,=\,\ \frac{{{{{(300)}}^{2}}}}{{3\ \,\times \,\ {{{10}}^{4}}}} = 3 m/s
Practice Questions (Basic Level)
Q.1
For which one of the following examples will the observed frequency of sound be greater than the true frequency?
(a) When the source of sound moves away from a stationary observer.
(b) When the source of sound moves in a circle with the observer at the centre.
(c) When the source of sound and the observer both move with the same speed in the same direction.
(d) When the observer moves towards a stationary source of sound.
Ans. (d)
Q.2
An electric train in Japan runs with a speed 1.3 mach. It is approaching a station and blows a whistle of frequency 800 Hz. The frequency of the whistle heard by a stationary observer on the platform is
(a) 800 Hz (b) 1600 Hz (c) 1040 Hz (d) insufficient data
Ans. (a)
Q.3
A sound source is moving towards a stationary observer with one-tenth of the speed of sound. The ratio of apparent to real frequency is
(a) {{(9/10)}^{2}}
(b) {{(11/10)}^{2}}
(c) 10/9
(d) 11/10
Ans. (c)
Q.4
A bullet passes past a person at a speed \mathbf{220}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound =\mathbf{330}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{1}}}}
(a) 0.67 (b) 0.8 (c) 1.2 (d) 3.0
Ans. (b)
Q.5
A source of sound is emitting a wave of wavelength 40 cm in air. If this source starts moving towards east with a velocity one-fourth the velocity of sound then the apparent wavelength of sound in a direction opposite to that of source will be
(a) 20 cm (b) 50 cm (c) 80 cm (d) 100 cm
Ans. (b)
Q.6
A sound source rotates anticlock wise with an angular velocity \omega . Radius of the circle is R. A person is at P. The maximum frequency is heared when position of the source is at
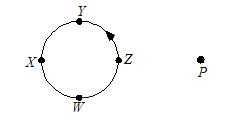
(a) Y (b) X (c) Z (d) W
Ans. (d)
Practice Questions (JEE Main Level)
Q.1
If the speed of sound in air is 340 m/s with what speed a tuning fork of frequency 300 Hz be rushed towards a reflecting wall so that 3 beats are produced per second?
(a) 3.4 m/s (b) 1.7 m/s (c) 17 m/s (d) 34 m/s
Ans. (b)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
