Video Lecture
Theory For Making Notes
Introduction
Kinematics is that branch of mechanics, which describes the motion of bodies without reference to the forces that either cause the motion or are generated as a result of the motion. Kinematics is often referred to as the ‘geometry of motion’.
Rest And Motion
An object is said to be in motion if its position changes with respect to its surroundings with time. On the other hand, if the position of the object does not change with respect to its surroundings, it is said to be at rest. A car speeding on the road, a ship sailing on water and a bird flying in air are examples of objects in motion. A book lying on a table is at rest because its position with respect to the table does not change with time.
Dimensions In Motion
The motion of an object is said to be one dimensional when only one of the three coordinates specifying the position of the object changes with time. The motion of a car on a road, the motion of a train along a railway track or an object falling freely are examples of one dimensional motion. One dimensional motion is also termed as rectilinear motion. The motion of an object is said to be two dimensional when two of the three coordinates specifying the position of the object change with time. The motion of a planet around the sun, a body moving along the circumference of a circle are examples of motion in two dimensions. Two dimensional motion is also referred to as motion in a plane.
Trajectory
The actual path followed by an object in a particular reference frame is termed as its “trajectory”. Thus, the trajectory is a straight line in case of one dimensional motion whereas in case of a two dimensional motion, the trajectory may be a circle, a parabola or in general, any curve.
Displacement And Distance
Displacement | Distance |
1. The displacement of a particle is defined as the difference between its final position and its initial position. We represent the displacement as Dx. Dx = xf – xi 2. Displacement is a vector quantity which has both magnitude and direction. 3. It can increase and decrease with time. 4. Depending on direction it can be positive or negative. | 1. The length of the actual path covered by a body in a time interval is called distance. 2. Distance is a scalar quantity which has magnitude only 3. It never decreases with time. 4. It is always positive |
Average Velocity and Average Speed
The average velocity of an object is defined as the ratio of its displacement to the time taken for that displacement
vav= \frac{{\Delta x}}{{\Delta t}}\,=\frac{{{{x}_{f}}-{{x}_{i}}}}{{{{t}_{f}}-\,{{t}_{i}}}}
The average speed of a particle is defined as the ratio of the total distance travelled to the time taken
Average speed = \displaystyle \frac{{Total\,\,distance\,\,travelled}}{{\Delta t}}
Note that: velocity and speed have different meanings. Velocity is a vector and speed is a scalar
Instantaneous Speed and Instantaneous Velocity
Instantaneous velocity is defined as the value approached by the average velocity when the time interval for measurement becomes closer and closer to zero, i.e. Δt → 0
Mathematically
v(t) = \underset{{\Delta t\to \,0}}{\mathop{{lim}}}\,\,{{v}_{{av}}}\,=\,\underset{{\Delta t\to \,0}}{\mathop{{lim}}}\,\,\frac{{\Delta x}}{{\Delta t}}
The instantaneous velocity function is the derivative of the displacement function with respect to the time
v(t) = \frac{{dx(t)}}{{dt}}
Graphical Analysis of Motion along a straight line
Average Velocity
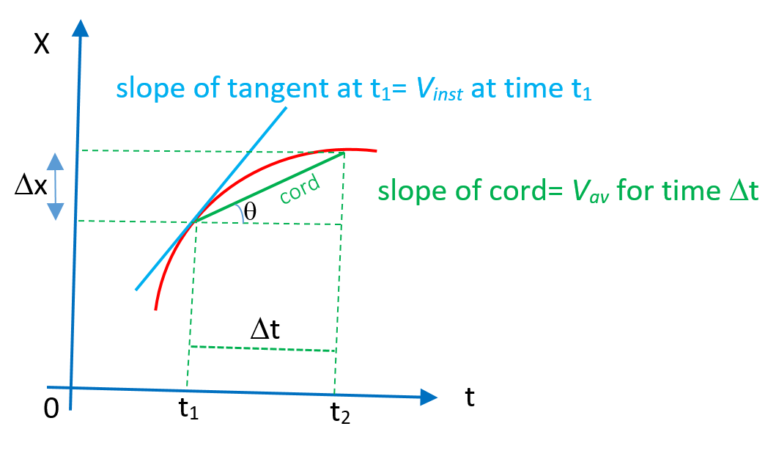
The average velocity between two points in a given time interval can be obtained from a displacement versus-time graph by computing the slope of the straight line joining the coordinates of the two points.
Instantaneous Velocity
The instantaneous velocity at time t is the slope of the tangent line drawn to the position-versus-time graph at that time.
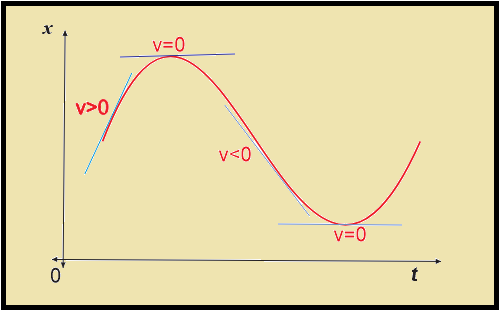
The position (x) versus time (t) graph of a particle whose velocity is not constant is shown in the diagram given below. In a given time interval Dt the slope of the chord joining two points on the curve gives the average velocity of the particle for that time interval. Whereas the instantaneous velocity at any point of time is equal to the slope of the tangent at that point on the curve.
Note :The direction of instantaneous velocity may be different from direction of average velocity
Uniform Motion in a Straight Line
A body is said to be in a uniform motion if it travels equal distance in equal intervals of time along a straight line.
A position(x) Vs time (t) graph for uniform motion is a straight line.
e.g., A vehicle running in a certain direction with the constant speed of 10 m/s will cover equal distances of 10 m in every second, so its motion will be uniform
For a uniform motion along a straight line in a given direction, the magnitude of the displacement is equal to the actual distance covered by the object.
Calculation Of Displacement and Distance
Case-1
When the body is in uniform motion The displacement and distance can be calculated very easily by simple relations
\displaystyle \text{Distance = Displacement = v}\times \text{t}
Since in uniform motion the direction of body remains fixed so we don’t bother about the direction.
Case-2
When the body reverses its direction and changes its speed instantly at the time of changing the direction.
For example the body moves for time t1 in the positive x direction with speed v1 and then for time t2 it moves along the negative x direction with speed v2.
So Distance = v1.t1 + v2.t2
and Displacement = v1.t1 – v2.t2
Case-3
If the veloity of body is changing with time i.e. v = f(t). Then again two cases arises
(A) If the sign of velocity i.e. direction of motion is not changing over the given time interval
(B) If the sign of velocity i.e. direction of motion is changing over the given time interval
Let the displacement or distance is to be calculated from time t1 to t2.
In case (A)
\displaystyle \text{Distance = Displacement = }\int\limits_{{{{t}_{1}}}}^{{{{t}_{2}}}}{{v(t).dt}}
In case (B)
\displaystyle \text{Displacement = }\int\limits_{{{{t}_{1}}}}^{{{{t}_{2}}}}{{v(t).dt}}
\displaystyle \text{Distance = }\left| {\int\limits_{{{{t}_{1}}}}^{{t’}}{{v(t).dt}}} \right|+\left| {\int\limits_{{t’}}^{{{{t}_{2}}}}{{v(t).dt}}} \right|
where t’ is the time instant at which the sign of velocity is changed.
Illustration
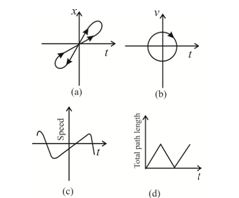
Look at the graphs (a) to (d) carefully and state with reasons, which of these cannot possibly represent one-dimensional motion of a particle
Solution
(a) No, graph (a) is not representing one-dimensional motion of a particle, because graph shows two different positions of the particle at same instant of time.
(b) It is not possible because when we go along the circular graph the time coordinate some time decreases and other time increases which is not possible. Also at a perticular instant there are two velocities of the body which is not possible.
(c) It is not possible because the speed can’t be negative
(d) It is not possible as the total length of path that is distance can’t decrease with time.
Illustration
The position of an object moving along x-axis is given by \displaystyle x\,=\,a+b{{t}^{2}}, where \displaystyle a=\,8.5\,\,m,\,\,b\,=\,2.5\,\,m/s and t is measured in seconds. What is its velocity at t = 0 s and
t = 2.0 s ? What is the average velocity between t = 2s and t = 4.0 s ?
Solution
We know that \displaystyle v\,=\,\frac{{dx}}{{dt}}
On differentiating w.r.t. t, we have
\displaystyle v\,=\,\frac{d}{{dt}}\left( {a\,+\,b{{t}^{2}}} \right)=2bt\,\,=\,\,5t\,\,m/s\,\,\,\left[ {\because \,\,\,b\,=\,2.5\,\,m} \right]
At \displaystyle t\,=\,0,\,\,v\,=\,0,\,\,t=2 and \displaystyle v\,=\,10\,\,m/s
Average velocity \displaystyle =\,\frac{{x\,\left( 4 \right)-x\left( 2 \right)}}{{4-2}}\,=\frac{{a+16b-a-4b}}{2}\,=\,6\times b\,=\,6\,\times \,2.5\,\,=\,\,15\,\,m/s
Illustration
A jogger starts his motion from the position x = 3m and reaches to a position x = 15m and then turns back and move to the position x = 1m. Find the total displacement and the total distance traveled by the jogger
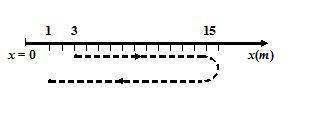
Solution
The initial and final displacements of the jogger are:
\displaystyle {{x}_{i}}=3m;\,\,{{x}_{f}}=1\text{m}
Therefore, displacement \displaystyle \Delta x={{x}_{f}}-{{x}_{i}}=1-3=-2m
distance = (15 – 3) + (15 – 1) = 12 + 14 = 26m
Note that : Displacement can be negative but distance can never be negative. Displacement is always less than or equal to distance. If the jogger returns back to its starting position, then displacement is zero but distance is still non-zero.
Illustration
A bird flies toward east at 10 m/s for 100 m. It then turns around and flies at 20 m/s for 15 s.
(a) Find its average speed
(b) Find its average velocity
Solution
Let us take the +ve x axis to point east and -ve x ais to point west. Now we need the total time interval. The first part of the journey took
Δt1 = (100 m)/ (10 m/s) = 10 s
and we are given Δt2 = 15 s for the second part. Hence the total time interval is
Δt = Δt1 + Δt2 = 25 s
The bird flies 100 m east and then (20 m/s)x(15 s) = 300 m west
(a) Average speed = \frac{{Distance}}{{\Delta t}}\,=\frac{{100\,m\,+\,300\,m}}{{25s}}\,=\,16\, m/s
(b) The net displacement is
Δx = Δx1 + Δx2 = 100 m – 300 m = -200 m
So that vav = \frac{{\Delta x}}{{\Delta t}}\,=\frac{{-200\,m}}{{25\,s}}\,= -8 m/s
The negative sign means that vav is directed toward the west.
Practice Questions (Level-1)
1.
A toy car travels from A to B at a constant speed v1 and without stopping at B returns to A at a constant speed v2 . Then the average speed of the car over the whole journey is
(a) \displaystyle \frac{{{{v}_{1}}+{{v}_{1}}}}{2}
(b) \displaystyle \frac{{2{{v}_{1}}{{v}_{2}}}}{{{{v}_{1}}+{{v}_{2}}}}
(c) \displaystyle \sqrt{{{{v}_{1}}{{v}_{2}}}}
(d) \displaystyle \frac{1}{{\frac{1}{{{{v}_{1}}}}+\frac{1}{{{{v}_{2}}}}}}
Ans. (b)
2.
If a body covers equal displacements in equal intervals of time, however small these intervals may be, its motion is
(a) accelerated motion
(b) uniform motion
(c) non–uniform motion
(d) none of the above
Ans. (b)
3.
A man leaves his house for a cycle ride. He comes back to his house after-an-hour after covering a distance of 1 km. What is his average velocity for the ride?
(a) \mathbf{0}\,\,\mathbf{km}\,\,{{\mathbf{h}}^{{-\mathbf{1}}}}
(b) \mathbf{2}\,\,\mathbf{km}\,\,{{\mathbf{h}}^{{-\mathbf{1}}}}
(c) \mathbf{2}\,\,\mathbf{km}\,\,{{\mathbf{s}}^{{-\mathbf{1}}}}
(d) \frac{\mathbf{1}}{\mathbf{2}}\,\,\mathbf{km}\,\,{{\mathbf{s}}^{{-\mathbf{1}}}}
Ans. (a)
4.
You observe an object covering distances in the direct proportion to the time elapsed. What conclusion might you draw about its acceleration?
(a) It is zero
(b) It is constant
(c) It is decreasing
(d) It is increasing
Ans. (a)
5.
In any journey, numerical value of ratio of displacement & distance must be
(a) 1
(b) ≥ 1
(c) ≤ 1
(d) zero
Ans. (c)
6.
In a journey the magnitude of velocity at a certain instant can be more than average speed.
(a) True
(b) False
(c) depends on direction of motion
(d) never
Ans. (a)
7.
A body with positive displacement cannot have negative velocity
(a) True
(b) False
(c) may be True
(d) None
Ans. (b)
8.
Read the statements carefully and choose the correct option
Statement-1 : If the displacement of the body is zero, the distance covered by it may not be zero.
Statement-2 : Displacement is a vector quantity and distance is a scalar quantity.
(a) Statement-1 is correct but Statement-2 is wrong
(b) Statement-2 is correct but Statement-1 is wrong
(c) Both the statements are correct
(d) Both the statements are wrong
Ans. (c)
9.
A car moves for half of its time at 80 km/h and for rest half of time at 40 km/h. What is the average speed of the car
(a) 80 km/h
(b) 60 km/h
(c) 40 km/h
(d) 100 km/h
Ans. (b)
10.
A wheel of radius 1 meter rolls forward half a revolution on a horizontal ground in 2 sec. The magnitude of the average velocity of the point of the wheel initially in contact with the ground is
(a) \displaystyle \pi
(b) \displaystyle \frac{\pi }{{\sqrt{2}}}
(c) \displaystyle \frac{{\sqrt{{{{\pi }^{2}}+4}}}}{2}
(d) \displaystyle \frac{\pi }{2}
Ans. (c)
Practice Questions (Level-2)
1.
In uniform motion
(a) The instantaneous speed may be greater than the magnitude of average velocity.
(b) The average speed may be greater than the magnitude of average velocity.
(c) The instantaneous speed may be less than the magnitude of instantaneous velocity.
(d) The magnitude of instantaneous speed ,instantaneous velocity, average speed and average velocity all are equal.
Ans : (d)
2.
At any instant during the motion if the velocity of a body is zero then
(a) Its displacement should also be zero
(b) Its distance travelled should also be zero
(c) Its displacement and distance may not be zero
(d)Its displacement must be zero but distance may not be zero
Ans : (c)
3.
At t = 3s a particle is at x = 7 m and has velocity v = 4 m/s. At t = 7s, it is at x = -5 m and has velocity v =-2 m/s. Find its average velocity.
(a) 3 m/s
(b) –3 m/s
(c) 4 m/s
(d) 2 m/s
Ans : (b)
4.
A point traversed half the distance with velocity vo. The remaining part of the distance was covered with velocity v1for half the time and with velocity v2for the other half of the time. Find the average velocity of the point over the whole time of motion.
(a) \displaystyle \frac{{2{{v}_{o}}\,({{v}_{1}}\,+\,{{v}_{2}})}}{{(2{{v}_{o}}\,+\,{{v}_{1}}\,+{{v}_{2}})}}
(b) \displaystyle \frac{{2{{v}_{o}}\left( {{{v}_{1}}-{{v}_{2}}} \right)}}{{\left( {2{{v}_{o}}+{{v}_{1}}+{{v}_{2}}} \right)}}
(c) \displaystyle \frac{{2{{v}_{o}}\left( {{{v}_{1}}+{{v}_{2}}} \right)}}{{\left( {2{{v}_{o}}+{{v}_{1}}-{{v}_{2}}} \right)}}
(d) \displaystyle \frac{{2{{v}_{o}}\,({{v}_{1}}\,-\,{{v}_{2}})}}{{(2{{v}_{o}}\,+\,{{v}_{1}}\,-{{v}_{2}})}}
Ans : (a)
5.
A particle moves according to the equation x = 2t2 – 5t + 6. Find average velocity in the first 3 s.
(a) 2 ms–1
(b) 4 ms–1
(c) 1 ms–1
(d) 4ms–1
Ans : (c)
6.
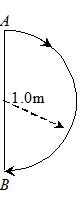
In 1.0 s, a particle goes from point A to point B , moving in a semicircle of radius 1.0 m. Find the magnitude of the average velocity and average speed of the particle.
(a) 2 m/s, 2.14 m/sec
(b) 4 m/s 4.14 m/sec
(c) 1 m/s, 1.14 m/sec
(d) 2 m/s, 3.14 m/sec
Ans. (d)
7.
For a moving particle (choose the correct statement)
(a) magnitude of average velocity > average speed
(b) magnitude of average velocity ≤ average speed
(c) magnitude of average velocity = average speed
(d) magnitude of average velocity ¹ 0 but average speed = 0
Ans. (b)
8.
A child wants to cross a mark on the road 15m away from his initial point. But he decide to move 5m forward and 3m backward and so on. If he takes 1sec for forward and backward motion each, find the time taken by him to cross the mark.
(a) 20sec
(b) 15sec
(c) 14 sec
(d) 11sec
Ans : (d)
9.
A body moves on a circle of radius r. From its starting point when its radius sweeps 120o at the center of circle the ratio of its average speed and average velocity is
(a) \displaystyle \frac{\pi }{{3\sqrt{3}}}
(b) \displaystyle \frac{{2\pi }}{{3\sqrt{3}}}
(c) \displaystyle \frac{\pi }{{\sqrt{3}}}
(d) \displaystyle \frac{{2\pi }}{{\sqrt{3}}}
Ans : (b)
10.
A body is moving on a straight line with velocity v= 6t2 m/sec . Find the average velocity in of the body from t=0 to t=2 sec. (Given at t=0 , x=0)
(a)12m/sec
(b) 6m/sec
(c) 8m/sec
(d) 10m/sec
Ans : (c)



