Video Lecture
Theory For Making Notes
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (Level-1)
1.
By corpuscular theory of light, the phenomenon which can be explained is
(a) Refraction
(b) Interference
(c) Diffraction
(d) Polarisation
Ans (a)
2.
According to corpuscular theory of light, the different colours of light are due to
(a) Different electromagnetic waves
(b) Different force of attraction among the corpuscles
(c) Different size of the corpuscles
(d) None of the above
Ans (c)
3.
Huygen’s conception of secondary waves
(a) Allow us to find the focal length of a thick lens
(b) Is a geometrical method to find a wavefront
(c) Is used to determine the velocity of light
(d) Is used to explain polarization
Ans (b)
4.
The idea of the quantum nature of light has emerged in an attempt to explain
(a) Interference
(b) Diffraction
(c) Radiation spectrum of a black body
(d) Polarisation
Ans (c)
5.
By a monochromatic wave, we mean
(a) A single ray
(b) A single ray of a single colour
(c) Wave having a single wavelength
(d) Many rays of a single colour
Ans (c)
6.
By Huygen’s wave theory of light, we cannot explain the phenomenon of
(a) Interference
(b) Diffraction
(c) Photoelectric effect
(d) Polarisation
Ans (c)
7.
Wavefront means
(a) All particles in it have same phase
(b) All particles have opposite phase of vibrations
(c) Few particles are in same phase, rest are in opposite phase
(d) None of these
Ans (a)
8.
Wavefront of a wave has direction with wave motion
(a) Parallel
(b) Perpendicular
(c) Opposite
(d) At an angle of q
Ans (b)
9.
Which one of the following phenomena is not explained by Huygen’s construction of wavefront
(a) Refraction
(b) Reflection
(c) Diffraction
(d) Origin of spectra
Ans (d)
10.
Which one of the following phenomena is not explained by Huygen’s construction of wavefront
(a) Refraction
(b) Reflection
(c) Diffraction
(d) Origin of spectra
Ans (d)
11.
Huygen’s principle of secondary wavelets may be used to
(a) Find the velocity of light in vacuum
(b) Explain the particle behaviour of light
(c) Find the new position of the wavefront
(d) Explain photoelectric effect
Ans (c)
12.
Select the right option in the following
(a) Christian Huygens a contemporary of Newton established the wave theory of light by assuming that light waves were transverse
(b) Maxwell provided the compelling theoretical evidence that light is transverse wave
(c) Thomas Young experimentally proved the wave behaviour of light and Huygens assumption
(d) All the statements give above, correctly answers the question “what is light”
Ans (b)
13.
A slit of width a is illuminated by white light. For red light (l = 6500 Å), the first minima is obtained at \theta ={{30}^{o}}. Then the value of a will be
(a) 3250 Å
(b) 6.5\times {{10}^{{-4}}}mm
(c) 1.24 microns
(d) 2.6\times {{10}^{{-4}}}cm
Ans (c)
14.
The light of wavelength 6328 Å is incident on a slit of width 0.2 mm perpendicularly, the angular width of central maxima will be
(a) {{0.36}^{o}}
(b) {{0.18}^{o}}
(c) {{0.72}^{o}}
(d) {{0.09}^{o}}
Ans (a)
15.
The bending of beam of light around corners of obstacles is called
(a) Reflection
(b) Diffraction
(c) Refraction
(d) Interference
Ans (b)
16.
The penetration of light into the region of geometrical shadow is called
(a) Polarisation
(b) Interference
(c) Diffraction
(d) Refraction
Ans (c)
17.
A slit of size 0.15 cm is placed at 2.1 m from a screen. On illuminated it by a light of wavelength 5 ´ 10–5 cm. The width of central maxima will be
(a) 70 mm
(b) 0.14 mm
(c) 1.4 mm
(d) 0.14 cm
Ans (c)
18.
A diffraction is obtained by using a beam of red light. What will happen if the red light is replaced by the blue light
(a) Bands will narrower and crowd full together
(b) Bands become broader and further apart
(c) No change will take place
(d) Bands disappear
Ans (a)
19.
Conditions of diffraction is
(a) \frac{a}{\lambda }=1
(b) \frac{a}{\lambda }>>1
(c) \frac{a}{\lambda }<<1
(d) None of these
Ans (a)
20.
Which statement is correct for a zone plate and a lens
(a) Zone plate has multi focii whereas lens has one
(b) Zone plate has one focus whereas lens has multiple focii
(c) Both are correct
(d) Zone plate has one focus whereas a lens has infinite
Ans (a)
21.
In Fresnel diffraction, if the distance between the disc and the screen is decreased, the intensity of central bright spot will
(a) Increase
(b) Decrease
(c) Remain constant
(d) None of these
Ans (b)
22.
A plane wavefront (\lambda =6\times {{10}^{{-7}}}m) falls on a slit v wide. A 0.4\,mmconvex lens of focal length 0.8\,m placed behind the slit focusses the light on a screen. What is the linear diameter of second maximum
(a) 6\,mm
(b) 12\,mm
(c) 3\,mm
(d) 9\,mm
Ans (a)
23.
A zone plate of focal length 60\,cm, behaves as a convex lens, If wavelength of incident light is 6000\,\,{\AA}, then radius of first half period zone will be
(a) 36\times {{10}^{{-8}}}m.
(b) 6\times {{10}^{{-8}}}m.
(c) \sqrt{6}\times {{10}^{{-8}}}m.
(d) 6\times {{10}^{{-4}}}m.
Ans (d)
Practice Questions (Level-2)
1.
A parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction pattern is formed on the screen placed perpendicular to the direction of incident beam. At the first minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of the slit is
(a) Zero
(b) \displaystyle \frac{\pi }{2}
(c) \displaystyle \pi
(d) 2 \displaystyle \pi
Ans :d
2.
A slit of width d is placed in front of a lens of focal length 0.5 m and is illuminated normally with light of wavelength 5.89 × 10–-7m. The first diffraction minima on either side of central diffraction maximum are separated by 2×10–3 m. The width d of the slit is
(a) 5.89 × 10–4 m
(b) 2.945 × 10–4 m
(c) 1.178 × 10–3 m
(d) 1.4725 × 10–4 m
Ans : b
3.
In a single slit diffraction experiment, as shown in fig, I0 is intensity at O corresponding to \displaystyle \theta = 0°. Then intensity at P, I( \displaystyle \theta ) if \displaystyle \lambda is the wavelength of light used is
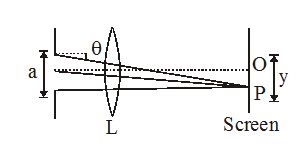
(a) \displaystyle I(\theta )\,=\,{{I}_{o}}\,\left\{ {\frac{{\sin \left( {\frac{{\pi a\,\sin \,\theta }}{\lambda }} \right)}}{{\frac{{\pi a\,\sin \,\theta }}{\lambda }}}} \right\}
(b) \displaystyle I(\theta )\,=\,{{I}_{o}}\,{{\left\{ {\frac{{\sin \left( {\frac{{\pi a\,\sin \,\theta }}{\lambda }} \right)}}{{\frac{{\pi a\,\sin \,\theta }}{\lambda }}}} \right\}}^{2}}
(c) \displaystyle I(\theta )\,=\,{{I}_{o}}\,\left\{ {\frac{{\sin \left( {\frac{{a\,\sin \,\theta }}{\lambda }} \right)}}{{\frac{{\pi a\,\sin \,\theta }}{\lambda }}}} \right\}
(d) \displaystyle I(\theta )\,=\,{{I}_{o}}\,\left\{ {\frac{{{{{\sin }}^{2}}\left( {\frac{{a\,\sin \,\theta }}{\lambda }} \right)}}{{\frac{{a\,\sin \,\theta }}{\lambda }}}} \right\}
Ans : b
4.
A beam of light of wavelength 600 nm from a distant source falls on a single slit 1 mm wide and the resulting diffraction pattern is observed on a screen 2 m away. The distance between the first dark fringes on either side of the central bright fringe is
(a) 1.2 cm
(b) 1.2 mm
(c) 2.4 cm
(d) 2.4 mm
Ans : d
5.
When the diffraction pattern from a certain slit illuminated with laser light ( \displaystyle \lambda = 6660Å) is projected on a screen 150 cm from the slit, the second minima on each side are separated by 8 cm. This tells us that
(a) the slit is approximately 0.005 cm wide
(b) the slit is approximately 0.05 cm wide.
(c) the slit is approximately 0.0025 cm wide
(d) the slit is approximately 0.025 cm wide.
Ans : a
6.
Diffraction occurs for all types of waves, including sound waves. High-frequency sound from a distant source with wave length 9.00 cm passes through a narrow slit 12.0 cm wide. A microphone is placed 40.0 cm directly in front of the center of the slit, corresponding to point O in figure. The microphone is then moved in a direction perpendicular to the line from the centre of the slit to point O. At what distances from O will the intensity detected by the microphone be zero?
(a) 44.5 cm
(b) –47.6 cm
(c)± 45.4 cm
(d) 42.7 cm
Ans : c
7.
Red light of wavelength 633 nm from a helium-neon laser passes through a slit 0.350 mm wide. The diffraction pattern is observed on a screen 3.00 m away. Define the width of a bright fringe as the distance between the minima on either side. (a) What is the width of the central bright fringe?
(a) 10.8 mm
(b) 11.6 mm
(c) 12.4 mm
(d) 13.5 mm
Ans : a
8.
Monochromatic light from a distant source is incident on a slit 0.750 mm wide. On a screen 2.00 m away, the distance from the central maximum of the diffraction pattern to the first minimum is measured to be 1.35 mm. Calculate the wavelength of the light.
(a) 506 nm
(b) 605 nm
(c) 504 nm
(d) 306 nm
Ans : aPolerization
9.
Unpolarised light falls on two polarizing sheets placed one over another. What must be the angle between their transmission axes if the intensity of light transmitted finally is one-third the intensity of the incident light? Assume that each polarizing sheet acts as an ideal polarizer.
(a) \displaystyle {{\cos }^{{-1}}}[\sqrt{{2/3}}]
(b) \displaystyle {{\cos }^{{-1}}}[\sqrt{{2/3}}]
(c) \displaystyle {{\cos }^{{-1}}}[\sqrt{{2/3}}]
(d) \displaystyle {{\cos }^{{-1}}}[\sqrt{{2/3}}]
Ans : a
10.
Unpolarized light of intensity 20.0 W/cm2 is incident on two polarizing filters. The axis of the first filter is at an angle of 25.0° counterclockwise from the vertical (viewed in the direction the light is traveling) and the axis of the second filter is at 62.0 counterclockwise from the vertical. What is the intensity of the light after it has passed through the second polarizer?
(a) 5.38 \displaystyle W/{{m}^{2}}
(b) 6.38 \displaystyle W/{{m}^{2}}
(c) 4.48 \displaystyle W/{{m}^{2}}
(d) 6.8 \displaystyle W/{{m}^{2}}
Ans : b
11.
Three polarizing filters are stacked, with the polarizing axis of the second and third filters at 23.0° and 62.0, respectively, to that of the first. If unpolarized light is incident on the stack, the light has intensity 75.0 W/cm2 after it passes through the stack. If the incident intensity is kept constant, what is the intensity of the light after it passed through the stack if the second polarizer is removed
(a) 34.2 \displaystyle W/{{m}^{2}}
(b) 43.2 \displaystyle W/{{m}^{2}}
(c) 32.3 \displaystyle W/{{m}^{2}}
(d) 42.3 \displaystyle W/{{m}^{2}}
Ans : c
