Video Lecture
Theory For Notes Making
WORK
The work W done by a constant force F when its point of application undergoes a displacement s is defined to be
W = F s cosθ …(1)
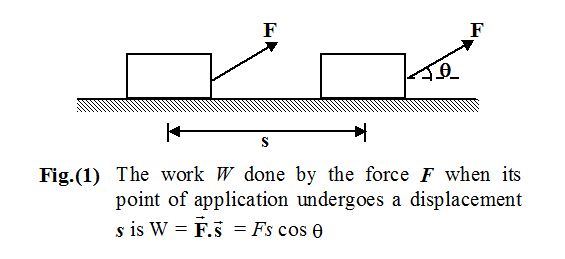
where θ is the angle between \displaystyle \vec{F} and \displaystyle \vec{s} as indicated in figure(1). Only the component of \displaystyle \vec{F} along s, that is , F cosθ, contributes to the work done. Strictly speaking, the work is done by the source or agent that applies the force. Work is a scalar quantity and its SI unit is the joule (J). From equation (1), we see that
1 J = 1 N-m
Work is also defined as the dot product of force and its displacement as given by equation (2)
W = \displaystyle \vec{F}.\vec{s}…(2)
In terms of rectangular components, the two vectors are \displaystyle \vec{F} = Fx \hat{k} + Fy \hat{j}+ Fz \hat{k}and
\displaystyle \vec{s} = Dx \hat{i} + Dy \displaystyle \hat{j} + Dz \hat{k}; hence, equation (2) may be written as
W = Fx Δx + Fy Δy + Fz Δz
The work done by a given force on a body depends only on the force, the displacement, and the angle between them. It does not depend on the velocity or the acceleration of the body, or on the presence of other forces.
Since the work is a scalar, its value also does not depend on the orientation of the coordinate axes. Since the magnitude of a displacement in a given time interval depends on the velocity of the frame of reference used to measure the displacement, the calculated work also depends on the reference frame.
Positive and Negative Work
Work done by a force may be positive or negative depending on the angle θ between the force and displacement. If the angle θ is acute (θ< 90o), then the component of force is parallel to the displacement and the work done is positive. (See figure 2 a)
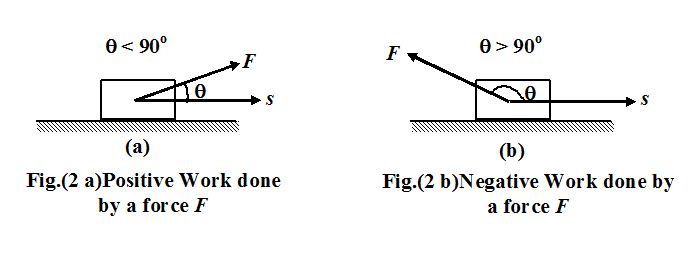
If the angle θ is obtuse (θ> 90o), then the component of force is antiparallel to the displacement and the work done by force is negative (see fig.(2 b)
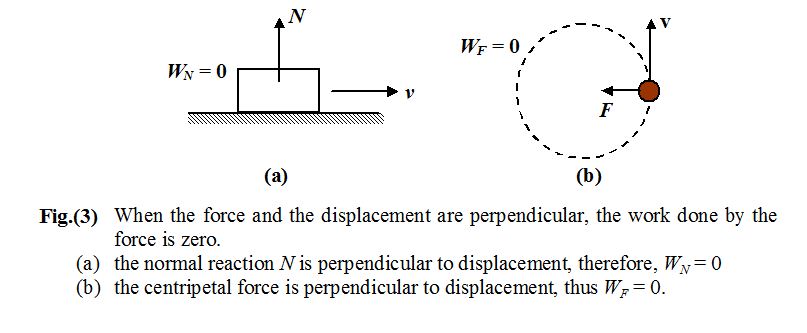
Zero Work Done
It is clear from the equation (1) that the work done by a force is zero when
(a) F = 0
(b) s = 0
(c) cos θ = 0 or θ = 90o
WORK DONE BY A VARIABLE FORCE
When the magnitude and direction of a force vary in three dimensions, it can be expressed as a function of the position vector \displaystyle \vec{F} (r), or in terms of the coordinates \displaystyle \vec{F} (x, y, z). The work done by such a force in an infinitesimal displacement ds is
dW = \displaystyle \vec{F}.d \displaystyle \vec{s}

The total work done in going from point A to point B as shown in the figure is
\displaystyle {{W}_{{A\to B}}}=\int\limits_{A}^{B}{{\vec{F}.d\vec{s}=}}\int\limits_{A}^{B}{{(F\cos \theta )ds}}
In terms of rectangular components,
\displaystyle {F} = Fx \hat{i} + Fy \hat{j} + Fz
\hat{k} and d \displaystyle {\vec{s}} = dx \displaystyle \hat{i} + dy \hat{j} + dz \hat{k}
therefore ,
WA – B= \int\limits_{{{{x}_{A}}}}^{{{{x}_{B}}}}{{{{F}_{x}}dx}}+\int\limits_{{{{y}_{A}}}}^{{{{y}_{B}}}}{{{{F}_{y}}dy}}+\int\limits_{{{{z}_{A}}}}^{{{{z}_{B}}}}{{{{F}_{z}}dz}}
Illustration
A box is moved over a horizontal path by applying force F = 60 N at an angle θ = 30o to the horizontal. What is the work done during the displacement of the box over a distance of 0.5 km.
Solution
By definition, W = F s cos θ
Here F = 60 N; s = 0.5 km = 500 m; θ = 30o.
W = (60)(500) cos30o = 26 kJ
Illustration
A load of mass m = 3000 kg is lifted by a winch with an acceleration a = 2 m/s2. Find the work done during the first one and a half seconds from the beginning of motion.
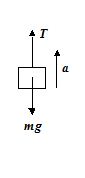
Solution
The height to which the body is lifted during the first t second is h = \frac{1}{2}a{{t}^{2}}.
The tension in the rope is given by
T = mg + ma
Work done is given by
W = Th = m(g + a) \left( {\frac{1}{2}a{{t}^{2}}} \right)
Here m = 3000kg, a = 2m/s2; g = 10m/s2; t = 1.5 s.
W = (3000)(10 + 2) \left[ {\frac{1}{2}\left( 2 \right){{{\left( {1.5} \right)}}^{2}}} \right]
or W = 81 kJ
Illustration
A block of mass 20 kg is to be raised from the bottom to the top of an incline 3 m long and 1 m off the ground at the top. Assuming the incline to be frictionless, how much work must be done by a force parallel to the incline pushing the block up? (g = 9.8 ms–2)
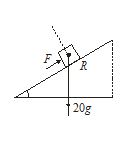
Solution
We have F = 20g sinq
and R = 20g cosq
or F=20g.\frac{1}{3}=\frac{{20g}}{3}\ \text{Newton} F=20g.\frac{1}{3}=\frac{{20g}}{3}\ \text{Newton}
Work done =Fx=\frac{{20g}}{3}.3=20\times 9.8=196\ \text{joule}.Ans.
POWER
The power delivered by an agent is the total work done by the agent divided by the total time interval
or P=\frac{{\Delta W}}{{\Delta t}}.
The instantaneous power of an agent is P=\frac{{dW}}{{dt}}
and W(\text{total work done)}=\int\limits_{{{{\mathbf{t}}_{\mathbf{1}}}}}^{{{{\mathbf{t}}_{\mathbf{2}}}}}{{Pdt.}}
We can easily find an alternative useful formula for power in terms of velocity. We have
P=\frac{{dW}}{{dt}}=\frac{{\overrightarrow{{F\,}}.\,\overrightarrow{{d\,}}x}}{{dt}}=\overrightarrow{{F\,}}.\left( {\frac{{\overrightarrow{{d\,}}x}}{{dt}}} \right)=\overrightarrow{{F\,}}.\overrightarrow{{v\,}}.
In SI the unit of power is joule per second (Js–1), which is called watt (W). The layman’s unit of power is horse power (H.P.) One horse power is equal to 746 watt.
Illustration
A block of mass 2kg is pulled up on a smooth incline of angle 30° with horizontal. If the block moves with an acceleration of 1m/s2, find the power delivered by the pulling force at a time 4 second after the motion has begun. What is the average power delivered during these four second after the motion starts?
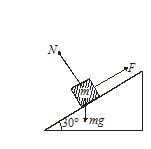
The force acting on the block are shown in figure.
Resolving forces parallel to incline,
F – mg sin θ = ma
F = mg sin q + ma
= 2 × 9.8 × sin 30° + 2 ×1
= 11.8 N
velocity = 0 + 1 × 4 = 4 m/s
Power delivered by force at t = 4 second
= Force × velocity = 11.8 × 4 = 47.2 W
The displacement during 4 second is given by the formula
v2 = u2 + 2aS
v2 = 0 + 2 × 1 × S
S = 8m
Work done in four second = Force × distance = 11.8 × 8 = 94.4J
average power delivered =Work done/time = 94.4/4 =23.6 Ans.
Objective Assignment
Q.1
A body moves a distance of 10 m along a straight line under the action of a force of 5 N. If the work done is 25 J, the angle which the force makes with the direction of motion of the body is
(a) 0o (b) 30o (c) 60o (d) 90o
Ans. (c)
Q.2
A body of mass m is moving in a circle of radius r with a constant speed v. The force on the body is mv2/r and is directed towards the center. What is the work done by the force in moving the body half the circumference of the circle:
(a) \frac{{m{{v}^{2}}}}{r}\times \pi rac
(b) zero
(c) \frac{{m{{v}^{2}}}}{{{{r}^{2}}}}
(d) \frac{{\pi {{r}^{2}}}}{{m{{v}^{2}}}}
Ans. (b)
Q.3
A particle moves along the x–axis from x = 0 to x = 5m under the influence of a force given by F = 7 – 2x + 3x2. The work done in the process is
(a) 70 (b) 270 (c) 35 (d) 135
Ans. (d)
Q.4
A person holds a bucket of weight 60 N. He walks 10 m along the horizontal and then climbs up a vertical distance of 5 m. The work done by the man is
(a) 300 J (b) 420 J (c) 720 J (d) none of these
Ans. (a)
Q.5
An engine develops 10 kW of power. How much time will it take to lift a mass of 200 kg to a height of 40 m( g = 10m/s2)
(a) 4 s (b) 5 s (c) 8s (d) 10 s
Ans. (c)
Q.6
Under the action of a force, a 2 kg body moves such that its position x as a function of time is given by x = \frac{{{{t}^{3}}}}{3}; where x is in meters and t in seconds the work done by the force in the first two seconds is
(a) 1600 J (b) 160 J (c) 16 J (d) 1.6 J
Ans. (c)
Q.7
An electric motor creates a tension of 4500 N in a hoisting cable and reels it in at the rate of 2 m/s. What is the power of this motor
(a) 25 kW (b) 9 kW (c) 225 W (d) 9000 hp
Ans. (b)
Q.8
A particle is acted upon by a conservative force \vec{F}=\left( {7\hat{i}-6\hat{j}} \right) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m), then
(a) work done by the force is 3 J
(b) work done by the force is -45 J
(c) at (0, 0) speed of the particle must be zero
(d) none of these
Ans. (b)
Q.9
Work done by force of friction
(a) can be positive
(b) can be negative
(c) can be zero
(d) all of the above
Ans. (d)
10.
A motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t according to
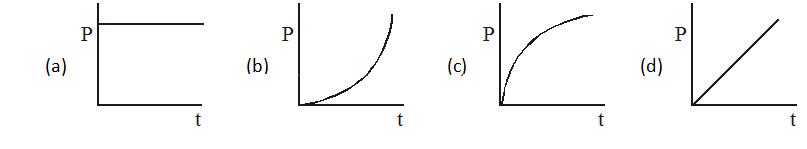
Ans (d)
11.
A force \overrightarrow{F}=(5\hat{i}+3\hat{j}) Newton is applied on a particle which displaces it from its origin to the point \overrightarrow{{r\,}}=(2\hat{i}-1\hat{j})metre. The work done on the particle is
(a) – 7J
(b) +13J
(c) +7J
(d) +11J
Ans (c)
12.
A machine which is 70% efficient raises a 10 kg body through a certain distance and spends 100 J of energy. The body is then released. On reaching the ground, the kinetic energy of the body will be
(a) 50J
(b) 35J
(c) 70J
(d) 100J
Ans (c)
13.
A vehicle is moving on a straight horizontal road with a constant velocity of 10 ms–1. The engine needs to spend 4kJ of energy per second. The force on the vehicle is
(a) 0.2 kN
(b) 0.4 kN
(c) 0.6 kN
(d) 1 N
Ans (b)
14.
A train weighing 1000 ton is moving on a horizontal track with a uniform velocity of 10 ms–1. The total resistance to the motion of the train is 5 kgf per ton. If g = 10 ms–2, then the power of the engine is
(a) 200 kW
(b) 400 kW
(c) 500 kW
(d) 800 kW
Ans (c)
15.
A electric motor creates a tension of 9000 N in cable and reels it in at the rate of 2ms–1. The power of the electric motor is
(a) 18 kW
(b) 15 kW
(c) 81 W
(d) 225 W
Ans (a)
16.
A crane is used to lift 1000 kg of coal from a mine 100 m deep. The time taken by the crane is 1 hour. The efficiency of the crane is 80%. If g = 10 ms–2, then the power of the crane is
(a) 104 W
(b) 105 W
(c) \frac{{{{{10}}^{4}}}}{{36\times 8}}\text{W}
(d) \frac{{{{{10}}^{5}}}}{{36\times 8}}\text{W}
Ans (d)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

