Video Lecture
Theory For Making Notes
IMPULSES AND MOMENTUM
Momentum
The linear momentum of particle is a vector quantity associated with quantity of motion. It is defined as product of mass of the particle and velocity of particle. i.e., linear momentum \overset{\to }{\mathop{P}}\, of a particle of mass m, moving with velocity \overset{\to }{\mathop{v}}\, is given by
\overset{\to }{\mathop{P}}\,\,\,=\,\,m\overset{\to }{\mathop{v}}\, … (i)
The direction of linear momentum is in the direction of velocity \overset{\to }{\mathop{v}}\, of the particle. The SI unit for linear momentum is kg ms–1 and its dimension is \displaystyle [ML{{T}^{{-1}}}]
Note That using Newton’s second law of motion we can relate linear momentum of particle and net force acting on it. The time rate of charge of linear momentum is equal to the resultant force acting on the particle.
This is, \overset{\to }{\mathop{F}}\,\,\,=\,\,\frac{{d\overset{\to }{\mathop{P}}\,}}{{dt}} … (ii)
Impulse of force and conservation of linear momentum
As we have seen, the force is related to momentum as
\overset{\to }{\mathop{F}}\,\,\,=\,\,\frac{{d\overset{\to }{\mathop{P}}\,}}{{dt}}
hence \overset{\to }{\mathop{F}}\,dt\,\,=\,\,d\overset{\to }{\mathop{P}}\,
If momentum of particle changes from {{\overrightarrow{P}}_{i}} to {{\overrightarrow{P}}_{f}} during a time interval of {{t}_{i}}ti to {{t}_{f}}tf, we can write
\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,\overset{{}}{\mathop{{dt}}}\,}}\,\,=\,\,\int\limits_{{{{{\overset{\to }{\mathop{P}}\,}}_{i}}}}^{{{{{\overset{\to }{\mathop{P}}\,}}_{f}}}}{{d\overset{\to }{\mathop{P}}\,}}
hence \int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overrightarrow{F}dt}}\,\,=\,\,{{\overrightarrow{P}}_{f}}-{{\overrightarrow{P}}_{i}}\,\,=\,\,\Delta \overrightarrow{P}
The quantity on the left hand side of this equation is called the impulse of force for the time interval \displaystyle {\Delta}t = {{t}_{f}} – {{t}_{i}} . Impulse is represented by \overset{\to }{\mathop{J}}\, and is given by
\overset{\to }{\mathop{J}}\,\,\,=\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,dt\,\,=\,\,\Delta \overrightarrow{P}}} … (iii)
That is, “The impulse of force equals the change in momentum of the particle.“ This statement called ‘impulse momentum theorem,’ is equivalent to Newton’s second law.
From the equation of impulse, we can see that impulse is a vector quantity having magnitude equal to the area under force-time curve as shown in figure by the shaded area.
Since the force can vary with time, we can define average force \overline{{\overrightarrow{F}}} as
\overline{{\overset{\to }{\mathop{F}}\,}}\,\,=\,\,\frac{1}{{\Delta t}}\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,dt}} …(iv)
Therefore we can also write,
\,\overline{{\overset{\to }{\mathop{F}}\,}}\,\,\Delta t=\Delta \overrightarrow{P} … (v)
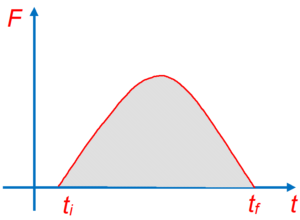
From the equation \overset{\to }{\mathop{F}}\,\,=\,\frac{{\overset{\to }{\mathop{{dP}}}\,}}{{dt}}, we can see that that if the resultant force is zero, the time derivative of the momentum is zero and therefore the linear momentum of a particle is constant. This is called ‘conservation of linear momentum. This conservation principle, we apply for a particle as well as system of particles also. Hence we can define conservation of linear momentum as
“If sum total of forces acting on a particle of system of particles is zero. The linear momentum of the system will remain conserved”.
Illustration
In a particular crash test, an automobile of mass 1500 kg collides with a wall as in figure (a). The initial and final velocities of the automobile are vi = 15.0 m/s and vf = 2.6 m/s. If the collision lasts for 0.150 s, find the impulse due to the collision and the average force exerted on the automobile.
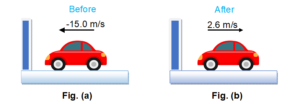
The initial and final momenta of the automobile are (taking rightward as positive)
\displaystyle {{p}_{i}} = m{{v}_{i}}=1500\times(-15.0)=-2.25\times{{10}^{4}} kg.m/s
\displaystyle {{p}_{f}} = m{{v}_{f}}=1500\times2.6 = 0.39\times{{10}^{4}} kg.m/s
Hence, the impulse is
\displaystyle J={\Delta} p ={{p}_{f}}-{{p}_{i}}=0.39\times{{10}^{4}}-{(-2.25)\times{{10}^{4}}} kg.m/s
\displaystyle J=2.64 \times {{10}^{4}} kg.m/s
The average force exerted on the automobile is given by
\overline{F}\,\,=\,\,\frac{{\Delta p}}{{\Delta t}}\,\,=\,\,\frac{{2.64\times {{{10}}^{4}}\,\mathbf{kg}\mathbf{.m/s}}}{{0.150s}} = 1.76 \times {{10}^{5}} N
Illustration
A baseball player uses a pitching machine to help him improve his batting average. He places the 50 kg machine on a frictionless surface . The machine fires a 0.15 kg baseball horizontally with a velocity of 36 m/s. What is the recoil velocity of the machine?
Solution:
We take the system, which consists of the baseball and the pitching machine. Because of the force of gravity and the normal force, the system is not really isolated. However, both of these forces are directed perpendicularly to the motion of the system. Therefore, momentum is constant in the x-direction because there are no external forces in this direction (as the surface is frictionless).
The total momentum of the system before firing is zero \displaystyle {{m}_{1}}{{v}_{1}}\hat {i} +{{m}_{2}}{{v}_{2}}\hat {i}=0 . Therefore, the total momentum after firing must be zero; that is, \displaystyle {{m}_{1}}{{v}_{1f}}\hat {i} +{{m}_{2}}{{v}_{2f}}\hat {i}=0 . With \displaystyle {m}_{1} = 0.15 kg, \displaystyle {{v}_{1}}\hat{i} = 36 m/s, With \displaystyle {m}_{2} = 50 kg, and solving for \displaystyle {v}_{2f}, we find the recoil velocity of the pitching machine to be
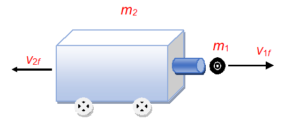
{{v}_{{2f}}}\,=\,\,-\frac{{{{m}_{2}}}}{{{{m}_{2}}}}\,\,{{v}_{1}}_{f}\,\,=\,\,-\,\left( {\frac{{0.15\,kg}}{{50\,\,kg}}} \right) (36 m/s) = -0.11 m/s
The negative sign for \displaystyle {v}_{2f} indicates that the pitching machine is moving to the left after firing, in the direction opposite the direction of motion of the cannon. In the words of Newton’s third law, for every force (to the left) on the pitching machine, there is an equal but opposite force (to the right) on the ball. Because the pitching machine is much more massive than the ball, the acceleration and consequent speed of the pitching machine are much smaller than the acceleration and speed of the ball.
Illustration
A cannon is mounted on a wagon, which stands on a straight section of the track. The mass of the wagon with the cannon, the shots and the men is M. The mass of the shot is m. When the cannon fires, the shot leaves with a muzzle velocity (relative to the cannon) \displaystyle v_{o} in a horizontal direction. Show that after n shots are fired the speed of the wagon is
m{{v}_{0}}\ \left[ {\frac{1}{M}\ +\ \frac{1}{{M\ -\ m}}\ +\ …\ +\ \frac{1}{{M\ -\ (n\ -\ 1)\ m}}} \right]
Solution
Before the first shot is fired, the gun is at rest and the momentum of system is zero. Since there are no external forces, the total momentum of the system after the first shot is fired must also be zero.
Let the velocity of the first shot be \displaystyle v_{1} and that of gun be \displaystyle V_{1} both relative to the ground.
Then,
\displaystyle m{{v}_{1}}+(M-m){V}_{1}=0
\displaystyle m({v}_{1}-{V}_{1}) + M{V}_{1} = 0
The velocity of the shot relative to the gun is \displaystyle {v}_{1}-{V}_{1} and this is the muzzle velocity of the shot.
\displaystyle {v}_{1}-{V}_{1} ={v}_{o}
therefore \displaystyle m{v}_{o}+M{V}_{1}=0
hence {{V}_{1}}\ =\ -\ \frac{{m{{v}_{0}}}}{M} … (i)
The second shot is fired when the gun is moving with a velocity \displaystyle V_{1} . The momentum of the system before the second shot is fired is \displaystyle (M – m){V}_{1}. By conservation of momentum the total momentum after second shot is fired is \displaystyle (M – m){V}_{1} .
If \displaystyle v_{2} and \displaystyle V_{2} are the velocities of the second shot and gun respectively relative to the ground,
\displaystyle mv_{2} + {(M – 2m)} {V}_{2} = (M – m){V}_{1}
\displaystyle mv_{2} –m{V}_{2}+ {(M – m)} {V}_{2} = (M – m){V}_{1}
hence m\frac{{({{v}_{2}}\ -\ {{V}_{2}})}}{{M\ -\ m}}\ +\ {{V}_{2}}\ =\ {{V}_{1}}
Since \displaystyle {v}_{2}-{V}_{2} is the velocity of the shot relative to the gun \displaystyle {v}_{2}-{V}_{2} ={v}_{o}
Thus \ {{V}_{2}}\ =\,\ {{V}_{1}}\,\ -\,\ \frac{{m{{v}_{0}}}}{{M\ -\ m}} =\ \,-\ \,\frac{{m{{v}_{0}}}}{M}\ \,-\ \,\frac{{m{{v}_{0}}}}{{M\ -\ m}} =\ \,-\ \,m{{v}_{0}}\ \left[ {\frac{1}{M}\ \,+\,\ \frac{1}{{M\ -\ m}}} \right]
The momentum of gun before third shot is fired is \displaystyle (M – 2m) {V}_{2}.
Let the velocity of shot relative to ground be \displaystyle v_{3} and that of gun \displaystyle {V}_{2}.
Proceeding in the same way the velocity of the wagon after third shot is fired can be seen to be given by
{{V}_{3}}\ \,=\ \,-\ \,m{{v}_{0}}\ \left[ {\frac{1}{M}\,\ +\,\ \frac{1}{{M\ -\ m}}\ \,+\,\ \frac{1}{{M\ -\ 2m}}} \right]
Proceeding in the same way the velocity of the wagon after n shots are fired will be given by
{{V}_{n}}\ =\,\ m{{v}_{0}}\ \left[ {\frac{1}{M}\,\ +\,\ \frac{1}{{M\ -\ m}}\,\ +\,\ \frac{1}{{M\ -\ 2m}}\ \,+\ \,…\,\ +\ \,\frac{1}{{M\ -\ (n\ -\ 1)\ m}}} \right]
Illustration
A block of mass 37.5 kg is placed on a table of mass 12.25 kg, which can move without friction on a level floor. A particle of mass 0.25 kg moving horizontally with velocity 302 m/s strikes the block inelastically (a) Find the distance through which the block moves relative to the table before they acquire a common velocity (b) also compute the common velocity, if the coefficient of friction between block and table is 0.25.
Solution:
(a) Applying the principle of conservation of momentum to the inelastic impact, we have
0.25 ´ 302 = (0.25 + 37.5 + 12.25)v, where v is the common velocity of the system.
Vcommon = \frac{{0.2\,\,\times \,\,302}}{{50}} = 1.51 m/s
(b) Let u be the velocity of block immediately after impact. Then, 0.25 x 302 = (0.25 + 37.5) u
u = \displaystyle \frac{{0.25\,\,\times \,\,302}}{{37.75}} = 2 m/s
Let \displaystyle a_{1} and \displaystyle a_{2} be the retardation of the block and acceleration of the table respectively.
Then (0.25 + 37.5) \displaystyle a_{1} = 12.25, \displaystyle a_{2}= kinetic frictional force
Because \displaystyle F_{k}={\mu}_{k}mg = 0.25 x [0.25 + 37.5] g = 0.25 x 37.75 g
\displaystyle a_{1} = 2.45 \frac{m}{s^{2}}
\displaystyle a_{2} = 7.55 \frac{m}{s^{2}}
Relative retardation of block = a1 + a2 = 2.45 + 7.55 = 10 \displaystyle \frac{m}{s^{2}}
hence v^{2} = 2 \times 10\times s
v = 2 m/s
4 = 20 s
s = \frac{4}{{20}}\,\,=\,\,\frac{1}{5}\,\,m = 0.2 m
Practice Questions (Basic Level)
1.
A 2 kg is moving at a speed of 6 m/s. How large a force F is needed to stop the block in a time of 0.5 ms?
(a) \displaystyle -4.4\times{{10}^{3}}N
(b) \displaystyle -2.4\times{{10}^{4}}N
(c) \displaystyle 2.4\times{{10}^{4}}N
(d) \displaystyle 4.4\times{{10}^{4}}N
Ans. (b)
2.
A ball falling with velocity {{\vec{v}}}_{i}=\left( {0.65\,\hat{i}-0.35\,\hat{j}} \right) m/s subjected to a net impulse \displaystyle \hat{J}=0.6\hat{i}+0.18\hat{j}\text{ Ns}. If the ball has a mass of 275 g, calculate its velocity immediately after following the impulse.
(a) \displaystyle \hat{v}_{f}=1.68\hat{i}+0.45\hat{j}\text{ m/s}
(b) \displaystyle \hat{v}_{f}=-2.68\hat{i}+0.14\hat{j}\text{ m/s}
(c) \displaystyle \hat{v}_{f}=1.53\hat{i}+0.305\hat{j}\text{ m/s}
(d) \displaystyle \hat{v}_{f}=-1.53\hat{i}-0.305\hat{j}\text{ m/s}
Ans. (c)
3.
An 150 g ball is thrown at 30 m/s. It is struck by a bat which gives it a velocity of 40 m/s in the opposite direction. If the time of contact is \displaystyle 10^{-2}s, what is the average force on the ball?
(a) -1050\,\hat{i}\,N
(b) -1750\,\hat{i}\,N
(c) 1050\,\hat{i}\,N
(d) -2057\,\hat{i}\,N
Ans. (a)
4.
A ball weighing 10 gm hits a hard surface vertically with a speed of 5 m/s and rebounds with the same speed. The bal remains in contact with the surface for 0.01 s. The average force exerted by the surface on the ball is
(a) 100 N
(b) 10 N
(c) 1 N
(d) 0.1 N
Ans. (b)
5.
If a stationary bomb explodes which of the following conditions will hold
(a) If the bomb explodes in two parts they may flyoff mutually opposite
(b) If the bomb explodes in three parts they may flyoff in different planes
(c) If the bomb explodes in four parts they may flyoff in different planes
(d) There may be a change in the momentum of the system during explosion
Ans. (c)
6.
Which of the following is a scalar
(a) Momentum
(b) Kinetic energy
(c) Impulsive force
(d) None of these
Ans. (b)
Practice Questions (JEE Main Level)
1.
A lead ball strikes a wall and falls down. A tennis ball having the same mass and velocity strikes the same wall and bounces back. Which is the correct statement
(a) The tennis ball suffers a greater change in momentum
(b) The lead ball suffers a greater change in momentum
(c) Both the balls suffers equal change in momentum
(d) The momentum of lead ball is greater than that of tennis ball
Ans. (a)
2.
A particle of mass 15 kg has an initial velocity {{\vec{v}}_{i}}=\hat{i}-2\hat{j} m/s. It collides with another body and the impact time is 0.1 s, resulting in a velocity {\vec{v}_{t}}=6\hat{i}+4\hat{j}+5\hat{k} m/s after impact. The average force of impact on the particle is
(a) 15\left( {5\hat{i}+6\hat{j}+5\hat{k}} \right) N
(a) 15\left( {5\hat{i}+6\hat{j}-5\hat{k}} \right) N
(c) 150\left( {5\hat{i}-6\hat{j}+5\hat{k}} \right) N
(d) 150\left( {5\hat{i}+6\hat{j}+5\hat{k}} \right) N
Ans. (d)
3.
If the linear momentum of a body is increased by \displaystyle 50\%, its KE will increase by
(a) \displaystyle 50\%
(b) \displaystyle 100\%
(c) \displaystyle 125\%
(d) \displaystyle 150\%
Ans. (c)
4.
The variation of momentum with time of one of the body in a two body collision is shown in figure.
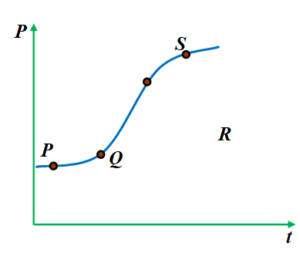
The instantaneous force is maximum corresponding to point
(a) P
(b) Q
(c) R
(d) S
Ans. (c)
5.
A particle of mass m moving with velocity u makes an elastic one-dimensional collision with a stationary particle of mass m. They are in contact for a very brief time T. Their force of interaction increases from zero to \displaystyle F_{o} linearly in time T/2, and decreases linearly to zero in further time T/2 as shown in the figure
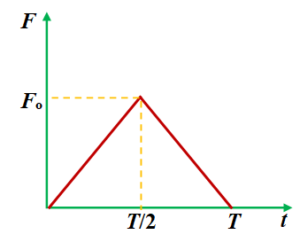
The magnitude of \displaystyle F_{o} is
(a) mu/T
(b) 2mu/T
(c) mu/2T
(d) none of these
Ans. (b)
6.
The magnitude of the impulse developed by a mass of 0.2 kg which changes its velocity from \displaystyle 5\,\hat{i}-3\hat{j}+7\hat{k}m/s to \displaystyle 2\,\hat{i}+3\hat{j}+\hat{k}m/s is
(a) 2.7 N-s
(b) 1.8 N-s
(c) 0.9 N-s
(d) 3.6 N-s
Ans. (b)
7.
A particle of mass 15 kg has an initial velocity \displaystyle {{v}_{i}}=\,\hat{i}-2\hat{j}. It collides with another body and the impact time is 0.1 s, resulting in a velocity \displaystyle {{\vec{v}}_{f}}=6\,\hat{i}+4\hat{j}+5\hat{k}m/s after impact. The average force of impact on the particle is
(a) \displaystyle 15|5\,\hat{i}+6\hat{j}+5\hat{k}|
(b) \displaystyle 15|5\,\hat{i}+6\hat{j}-5\hat{k}|
(c) \displaystyle 150|5\,\hat{i}-6\hat{j}+5\hat{k}|
(d) \displaystyle 150|5\,\hat{i}+6\hat{j}+5\hat{k}|
Ans. (d)
8.
A unidirectional force F varying with time t as shown in the figure acts on a body initially at rest for a short duration 2T.
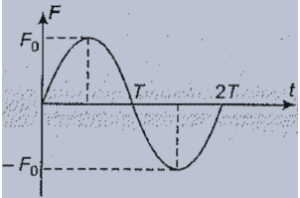
Then, the velocity acquired by the body is
(a) \displaystyle \frac{{\pi {{F}_{0}}T}}{{4m}}
(b) \displaystyle \frac{{\pi {{F}_{0}}T}}{{2m}}
(c) \displaystyle \frac{{{{F}_{0}}T}}{{4m}}
(d) zero
Ans. (d)
9.
A player takes 0.1 s in catching a ball of mass 150 g moving with velocity of 20 m/s. The force imparted by the ball on the hands of the player is
(a) 0.3 N
(b) 3 N
(c) 30 N
(d) 300 N
Ans. (c)
Practice Questions (JEE Advance Level)
Question no. 1 and 2
A 6 gm tennis ball strikes the ground at 25 m/s at 40° to the horizontal. It bounces off at 20 m/s at 30° to the horizontal as shown in the figure.
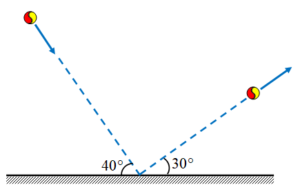
1.
Find the impulse exerted on the ball.
(a) -0.28\,\hat{i}+4.56\hat{j} kg m/s
(b) -0.11\,\hat{i}+1.56\hat{j} kg m/s
(c) 1.2\,\hat{i}-2.56\hat{j} kg m/s
(d) 0.11\,\hat{i}-1.56\hat{j} kg m/s
Ans. (b)
2.
If the collision lasted 5 ms, find the average force exerted on the ball by the court.
(a) -22\,\hat{i}+312\hat{j} N
(b) 22\,\hat{i}-312\hat{j} N
(c) -42\,\hat{i}+212\hat{j} N
(d) 25\,\hat{i}-300\hat{j} N
Ans. (a)
3.
A chain of length L and linear mass density \displaystyle \lambda is kept in a vertical position with its lower end touching the floor. The upper end of the chain is left and the chain is allowed to fall freely under gravity. When x length of the chain comes on the floor the force acting on the floor is \displaystyle n\lambda gx . Here n is
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (c)
4.
A uniform chain AB of length 2L having linear mass density \displaystyle \lambda is hanging from the ceiling of an elevator by two light threads AA’ and BB’ of equal length.(AB is negligible) as shown in the figure.
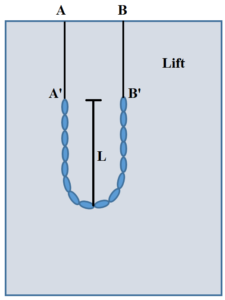
At a certain instant the elevator starts ascending with constant acceleration a. Two seconds after begining of motion thread BB’ is burnt. Assuming the instant as t=0, then the tension in the thread AA’ at any time t must be
(a) \displaystyle T=\lambda \left( {L+\frac{3}{4}(g+a){{t}^{2}}} \right){{(g+a)}^{2}}
(b) \displaystyle T=\lambda \left( {L+\frac{1}{4}(g+a){{t}^{2}}} \right)(g+a)
(c) \displaystyle T=\lambda \left( {2L+\frac{3}{4}(g+a){{t}^{2}}} \right)(g+a)
(d) \displaystyle T=\lambda \left( {L+\frac{3}{4}(g+a){{t}^{2}}} \right)(g+a)
Ans. (d)
5.
Two balls A and B of same mass m are attached at the ends of a string of length 2L. The system is placed on a smooth horizontal surface with the distance between the balls equal to L as shown in figure
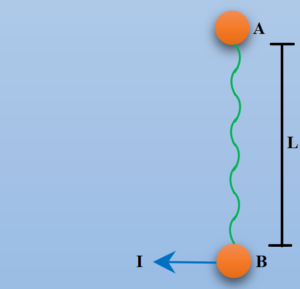
An impulse I is given to ball B in a direction perpendicular to the line joining A and B. Then the velocity of ball A just after the string becomes taut must be
(a) \displaystyle {{v}_{A}}=\frac{{\sqrt{5}I}}{{2m}}
(b) \displaystyle {{v}_{A}}=\frac{{\sqrt{3}I}}{{4m}}
(c) \displaystyle {{v}_{A}}=\frac{{\sqrt{2}I}}{{m}}
(d) \displaystyle {{v}_{A}}=\frac{{\sqrt{3}I}}{{2m}}
Ans. (b)



