Video Lecture
Theory For Making Notes
Momentum
The linear momentum of particle is a vector quantity associated with quantity of motion. It is defined as product of mass of the particle and velocity of particle. i.e., linear momentum \overset{\to }{\mathop{P}}\, of a particle of mass m, moving with velocity \overset{\to }{\mathop{v}}\, is given by
\overset{\to }{\mathop{P}}\,\,\,=\,\,m\overset{\to }{\mathop{v}}\,
Remember that the direction of linear momentum is always taken in the direction of velocity \overset{\to }{\mathop{v}}\, of the particle. The SI unit for linear momentum is kg ms–1 and its dimension is [MLT–1].
Newton’s second law of motion :
Through Newton’s second law we can relate linear momentum of particle and net force acting on it. The time rate of charge of linear momentum is equal to the resultant external force acting on the particle.
Hence \overset{\to }{\mathop{F}}\,\,\,=\,\,\frac{{d\overset{\to }{\mathop{P}}\,}}{{dt}}
Also remember that the direction of change in momentum \,d\overset{\to }{\mathop{P}}\, is always same as that of the net external force \overset{\to }{\mathop{F}}\, acting on the body.
Impulse of force
As we know that the force is related to momentum as
\overset{\to }{\mathop{F}}\,\,\,=\,\,\frac{{d\overset{\to }{\mathop{P}}\,}}{{dt}}
\overset{\to }{\mathop{F}}\,dt\,\,=\,\,d\overset{\to }{\mathop{P}}\,
If momentum of particle changes from {{\overrightarrow{P}}_{i}} to {{\overrightarrow{P}}_{f}} during a time interval of ti to tf, we can write
\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,\overset{{}}{\mathop{{dt}}}\,}}\,\,=\,\,\int\limits_{{{{{\overset{\to }{\mathop{P}}\,}}_{i}}}}^{{{{{\overset{\to }{\mathop{P}}\,}}_{f}}}}{{d\overset{\to }{\mathop{P}}\,}} Þ \int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overrightarrow{F}dt}}\,\,=\,\,{{\overrightarrow{P}}_{f}}-{{\overrightarrow{P}}_{i}}\,\,=\,\,\Delta \overrightarrow{P}
The quantity on the left hand side of this equation is called the impulse of force for the time interval Dt = tf – ti. Impulse is represented by \overset{\to }{\mathop{J}}\, and is given by
\overset{\to }{\mathop{J}}\,\,\,=\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,dt\,\,=\,\,\Delta \overrightarrow{P}}} … (iii)
That is, “The impulse of force equals the change in momentum of the particle.“ This statement called ‘impulse momentum theorem,’ is equivalent to Newton’s second law.
From the equation of impulse, we can see that impulse is a vector quantity.
Let us say that a variable force is acting on a body whose graph is shown in the diagram given below. Then the magnitude of impulse is equal to the area under force-time graph as shown in figure by the shaded area.
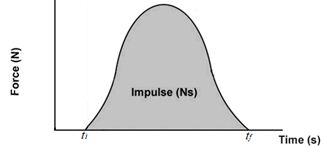
Since the force can vary with time, we can define average force ( {{\vec{F}}_{{av}}}) as {{\overset{\to }{\mathop{F}}\,}_{{av}}}\,\,=\,\,\frac{{\Delta \overset{\to }{\mathop{P}}\,}}{{\Delta t}}
But we know that \Delta \overrightarrow{P}\,=\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,dt\,}}
Therefore {{\vec{F}}_{{av}}}\,\,=\,\,\frac{1}{{\Delta t}}\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,dt}}
From equation {{\overset{\to }{\mathop{F}}\,}_{{av}}}\,\,=\,\,\frac{{\Delta \overset{\to }{\mathop{P}}\,}}{{\Delta t}} we conclude that to change the momentum of a body some external force is required. Here Δt is the time of contact between the force and the body or we can also say that it is the time available for changing the momentum.
So if time of contact Δt is increased, average force is decreased and vice-versa.
This concept gives explanation of many questions where the momentum of a system is changed in a large time just to decrease the force.
For example
(i)
In catching a ball a player by drawing his hands backwards increases the time of contact and so, lesser force acts on his hands and his hands are saved from getting hurt.
(ii) In jumping on sand (or water) the time of contact is increased due to yielding of sand or water so force is decreased and we are not injured. However if we jump on cemented floor the motion stops in a very short interval of time resulting in a large force due to which we are seriously injured.
Whereas in some cases we can increase the force by decreasing the time of contact or by applying sudden force called impact on a body. For example In hitting or kicking a ball we decrease the time of contact so that large force acts on the ball producing greater acceleration
In all cases of Hitting, kicking, collision etc. the time is negligibly small where as the force is variable and reaches a extremely large magnitude as shown in the graph given below.
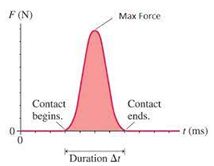
In all such cases an impulse acts on the body which is equal to the change in momentum as given by the following equation
\overset{\to }{\mathop{J}}\,\,\,=\,\,\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\overset{\to }{\mathop{F}}\,\,dt\,\,=\,\,\Delta \overrightarrow{P}}}
Illustration
Figure shows the variation of force acting on a body with time. Calculate the impulse of this force.
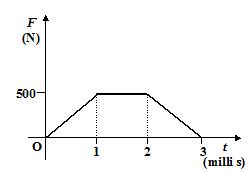
Solution
Impulse of a force is the area under the graph.
Thus
J= \left[ {\frac{1}{2}\left( {500} \right)\left( 1 \right)+\left( {500} \right)\left( {2-1} \right)+\frac{1}{2}\left( {500} \right)\left( {3-2} \right)} \right]{{10}^{{-3}}}
or J = [250 + 500 + 250]10-3
or J = 1 Ns
Illustration
An 150 g ball is thrown at 30 m/s. It is struck by a bat which gives it a velocity of 40 m/s in the opposite direction. If the time of contact is 10-2s, what is the average force on the ball?
Solution
If we choose the original direction as +x axis, then
The average force is
Fav= \frac{{\Delta p}}{{\Delta t}}=\frac{{-0.15kg\times 70\,\hat{i}}}{{{{{10}}^{{-2}}}}}=-1050\,\hat{i}\,N
Notice that this is much larger than the weight (1.5 N) of the ball.
Illustration
Find the impulse due to the force \displaystyle \vec{F} = a\,\hat{i}+bt\,\hat{j}, where a = 2N and b = 4 N/s, if this force acts from ti= 0 to tf= 0.3 s.
Solution
As we know that \overrightarrow{J}=\int\limits_{{{{t}_{i}}}}^{{{{t}_{f}}}}{{\vec{F}dt}}= \int\limits_{0}^{{0.3}}{{\left( {a\,\hat{i}+bt\,\hat{j}} \right)}}dt
or \overrightarrow{J}=a\,\hat{i}\int\limits_{0}^{{0.3}}{{dt}}+b\,\hat{j}\int\limits_{0}^{{0.3}}{{tdt}}
or \overrightarrow{J}=\left| {at\,\hat{i}\,\,} \right|_{0}^{{0.3}}+\left| {\frac{{b{{t}^{2}}}}{2}\hat{j}} \right|_{0}^{{0.3}}
or \overrightarrow{J} = (2)(0.3) \hat{i}+ \frac{{\left( 4 \right){{{\left( {0.3} \right)}}^{2}}}}{2}\hat{j}
thus \overrightarrow{J} = (0.6 \hat{i} + 0.18 \hat{j}) Ns
Illustration
In a particular crash test, an automobile of mass 1500 kg collides with a wall as in figure (a). The initial and final velocities of the automobile are vi = 15.0 m/s and vf = 2.6 m/s. If the collision lasts for 0.150 s, find the impulse due to the collision and the average force exerted on the automobile.
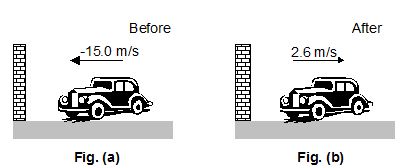
Solution
The initial and final momenta of the automobile are (taking rightward as positive)
pi = mvi = (1500 kg) (-15.0 m/s) = 2.25 × 104kg.m/s
pf = mvf = (1500 kg) (2.6 m/s) = 0.39 × 104kg.m/s
Hence, the impulse is
J = Δp = pf – pi = 0.39 × 104kg.m/s – (–2.25 × 104kg.m/s)
J = 2.64 × 104kg.m/s
The average force exerted on the automobile is given by
\overline{F}\,\,=\,\,\frac{{\Delta p}}{{\Delta t}}\,\,=\,\,\frac{{2.64\times {{{10}}^{4}}\,\mathbf{kg}\mathbf{.m/s}}}{{0.150s}}= 1.76 × 105 N
CONSERVATION OF LINEAR MOMENTUM
When the sum of the forces on an object is zero, the equation
\displaystyle {{\vec{F}}_{{net}}}=\frac{{d\vec{P}}}{{dt}}
Tell us that the time derivative of momentum is zero.
That is, \displaystyle \frac{{d\vec{P}}}{{dt}}=0
This implies \displaystyle \vec{P}= constant
Consequently, one can state a conservation law for momentum:
When the net force on a particle is zero, its momentum is constant.
The real utility of the momentum conservation concept comes about when it is applied to a collection of particles. For a system of particles, the total momentum is simply the vector sum of the momentum of each of the particles in the system. That is
\displaystyle {{\vec{F}}_{{net}}}=\sum{{({{{\vec{F}}}_{{ext}}}+}}{{\vec{F}}_{{\operatorname{int}}}}) (9)
Now consider the net force on a system of particles.
There are two kinds of forces:
(i)
Internal forces, resulting from the forces between the particles within the system, and
(ii)
External forces, arising from the forces between the particles in the system and objects outside the system.
For example, consider a system of two blocks joined together with a spring. If the system is allowed to fall freely under gravity, then the gravitational force acting on each block is the external force and the spring force acting on each block is internal.
When we calculate the net force on a system of particles by performing the vector sum of all the forces then \displaystyle {{\vec{F}}_{{net}}} is the summation of all the internal and external forces and can be written as \displaystyle {{\vec{F}}_{{net}}}=\sum{{({{{\vec{F}}}_{{ext}}}+}}{{\vec{F}}_{{\operatorname{int}}}}) . But the vector sum of all internal forces acting within the system is always zero because they exist in equal and opposite pairs.
Hence \displaystyle \sum{{{{{\vec{F}}}_{{\operatorname{int}}}}}}=0 and therefore \displaystyle {{\vec{F}}_{{net}}}=\sum{{({{{\vec{F}}}_{{ext}}})}}
Now we can write Newton’s second law \displaystyle {{\vec{F}}_{{net}}}=\frac{{d\vec{P}}}{{dt}} as
or \displaystyle \sum{{{{{\vec{F}}}_{{ext}}}}}=\frac{{d\vec{P}}}{{dt}} (10)
Now, if the summation of external forces is zero, then
\displaystyle \frac{{d\vec{P}}}{{dt}}=0
Thus,
\displaystyle \vec{P} = constant (that is the linear momentum of the system remains conserved)
Law of Conservation of Momentum
So we can state the conservation of linear momentum as follows:
In the absence of a net external force, the linear momentum of a system is conserved.
The conservation of momentum law can be used to relate the initial motion of particles within a system to the motion of those same particles sometime later. The law emphasizes the equality of momentum before and after something happens within the system.
Thus, the conservation law is usually written as
\displaystyle {{\vec{P}}_{{initial}}}={{\vec{P}}_{{final}}}\sum\limits_{{i=1}}^{N}{{{{P}_{i}}}}=\sum\limits_{{f=1}}^{N}{{{{P}_{f}}}}
Recoiling of a gun :
For bullet and gun system, the force exerted by trigger will be internal so the momentum of the system remains conserved. Here system means gun + bullet

Let {{m}_{G}}= mass of gun, {{m}_{B}}=mass of bullet,
{{v}_{G}}= velocity of gun , {{v}_{B}}=velocity of bullet
(Note that both the velocities are in the ground frame)
Initial momentum of system = 0 (Before firing)
Final momentum of system ={{m}_{G}}{{\vec{v}}_{G}}+{{m}_{B}}{{\vec{v}}_{B}} (After firing)
By the law of conservation of linear momentum
{{m}_{G}}{{\vec{v}}_{G}}+{{m}_{B}}{{\vec{v}}_{B}}=0
So recoil velocity {{\vec{v}}_{G}}=-\frac{{{{m}_{B}}}}{{{{m}_{G}}}}\,{{\vec{v}}_{B}}
(a)
Here negative sign indicates that the velocity of recoil {{\vec{v}}_{G}} is opposite to the velocity of the bullet.
(b)
{{v}_{G}}\propto \frac{1}{{{{m}_{G}}}} i.e. higher the mass of gun, lesser the velocity of recoil of gun.
Illustration
A baseball player uses a pitching machine to help him improve his batting average. He places the 50-kg machine on a frictionless surface as in figure. The machine fires a 0.15 kg baseball horizontally with a velocity of 36 m/s. What is the recoil velocity of the machine?
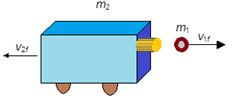
Solution:
We take the system, which consists of the baseball and the pitching machine. Because of the force of gravity and the normal force, the system is not really isolated. However, both of these forces are directed perpendicularly to the motion of the system. Therefore, momentum is constant in the x-direction because there are no external forces in this direction (as the surface is frictionless).
The total momentum of the system before firing is zero (m1v1i +m2v2i = 0). Therefore, the total momentum after firing must be zero; that is, m1v1f +m2v2f = 0
With m1 = 0.15 kg, v1i = 36 m/s, and m2 = 50 kg, solving for v2f, we find the recoil velocity of the pitching machine to be
{{v}_{{2f}}}\,=\,\,-\frac{{{{m}_{2}}}}{{{{m}_{2}}}}\,\,{{v}_{1}}_{f}\,\,=\,\,-\,\left( {\frac{{0.15\,kg}}{{50\,\,kg}}} \right) (36 m/s) = –0.11 m/s
The negative sign for v2f indicates that the pitching machine is moving to the left after firing, in the direction opposite the direction of motion of the cannon. In the words of Newton’s third law, for every force (to the left) on the pitching machine, there is an equal but opposite force (to the right) on the ball. Because the pitching machine is much more massive than the ball, the acceleration and consequent speed of the pitching machine are much smaller than the acceleration and speed of the ball.
Illustration
A man moving on a platform (or boat) kept on a frictionless surface.

When a man moves on a boat ,the frictional force acting between his feet and boat acts as an internal force therefore it cannot change the momentum of system (boat+man). Hence the conservation of momentum is applicable. This can be understood by the following solved example.
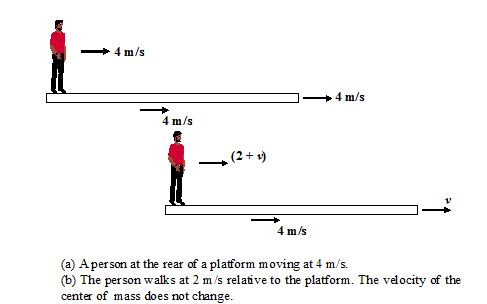
A 75 kg man stands at the rear end of a platform of mass 25 kg and length 4m, which moves initially at 4 \hat{i} m/s over a frictionless surface. At t = 0, he walks at 2 m/s relative to the platform and then stops at the front end. During the period of walking, find the displacement of
(a) the platform,
(b) the man
Solution
Initially the man, the platform, and the cm have the same velocity, 4 \hat{i}m/s, as shown in the figure. When he begins to walk forward, his increase in momentum must be compensated for by a decrease in the platform’s momentum. Let us say that the velocity of the platform relative to the ground while he is walking i.e.
\displaystyle {{\vec{v}}_{{PG}}} ={{v}_{p}}\hat{i}
The velocity of man relative to the ground is then
\displaystyle {{\vec{v}}_{{MG}}}={{\vec{v}}_{{MP}}}+/katex]{{\vec{v}}_{{PG}}}[.= (2 + <em>v<sub>P</sub></em>) 4 \hat{i}.
From the conservation of momentum, we have
(75 + 25) x 4 = 75( 2 + vp) + 25 vP
Thus, the velocity of the platform is vP= 2.5 m/s, and
The velocity of the man is vm= 4.5 m/s.
Since the velocity of man relative to platform is 2 m/s,
Therefore, it takes
t = \frac{{4m}}{{2m/s}}=2s
to walk from the rear to the front.
Displacement of platform is
xp= vpt= (2.5)(2) = 5 m
Displacement of the man is
Xm= vmt= (4.5)(2) = 9 m
SYSTEM OF VARIABLE MASS
So far we have dealt with the dynamics of a system whose mass is constant. We now wish to discuss the dynamics of a system, such as a rocket, whose mass varies. One may try to apply the following equation in such a case.
\displaystyle {{\vec{F}}_{{ext}}}=\frac{{d\vec{P}}}{{dt}}=M\frac{{d\vec{v}}}{{dt}}+\vec{v}\frac{{dM}}{{dt}} (1))
However, this equation is correct in only a few very special cases. This approach is not correct when mass actually enters or leaves the system.
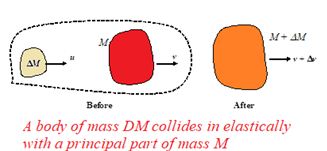
Let us examine the motion of a body of mass M, moving with velocity v. Another small body of mass M approaches with velocity u along the same line. We assume u >v and that after the collision the two bodies stick together and move at velocity (v + v), as shown in the figure.
By defining the system comprises both the bodies we can use \displaystyle \sum{{{{{\vec{F}}}_{{ext}}}}}=\frac{{d\vec{P}}}{{dt}}
, where i \displaystyle \vec{P} is the total momentum of the system of constant mass, M + M. The change in momentum of the system in time t is
P = (M + M)(v + v) – Mv– Mu
= Mv – (u – v)M
Now (u – v) = vrel is the velocity of M relative to M before the collision.
We divide both sides of this equation by t and take the limit as t’ 0:
\displaystyle {{\vec{F}}_{{ext}}}=\frac{{d\vec{P}}}{{dt}}=M\frac{{d\vec{v}}}{{dt}}+\vec{v}\frac{{dM}}{{dt}} (2)
Note how equation (2) differs from equation (1), the sign of the second term is negative and \displaystyle \vec{v} is replaced by \displaystyle {{\vec{v}}_{{rel}}}. The reason for this discrepancy is that the expression
\displaystyle \vec{P}=M\vec{v} for the total momentum is valid only if we take \displaystyle \vec{v} to be \displaystyle {{\vec{v}}_{{cm}}} . In equation (), \displaystyle \vec{v} refers to the velocity of just the principal part of the system.
It is convenient to rewrite it in the form
\displaystyle M\frac{{d\vec{v}}}{{dt}}={{\vec{F}}_{{ext}}}+{{\vec{v}}_{{rel}}}\frac{{dM}}{{dt}} (3)
The acceleration \displaystyle \frac{{d\vec{v}}}{{dt}} of the principal part, whose instantaneous mass is M, is determined.
By \displaystyle {{\vec{F}}_{{ext}}}, the net external force on the whole system (of constant mass M + ÄM), and
By \displaystyle {{\vec{v}}_{{rel}}}\frac{{dM}}{{dt}} , which is the rate at which momentum is being transferred into, or out, the principal part. It is also called the thrust force or reactive force.
\displaystyle {{\vec{F}}_{{thrust}}}={{v}_{{rel}}}\frac{{dM}}{{dt}}
ROCKET PROPULSION
Consider a rocket of mass M with fuel of mass Äm. Their common velocity is v relative to some inertial frame. When the rocket engines are fired, the gases expelled backward with an exhaust velocity \displaystyle {{\vec{v}}_{{ex}}} = –vex \hat{i} relative to the rocket. This is a fixed quantity determined by the design of the engine and the type of fuel. If the rocket’s velocity changes to v+\Delta v relative to the inertial frame, then the velocity of gas with respect to the frame will be
\displaystyle {{\vec{v}}_{{gas}}}={{\vec{v}}_{{ex}}}+\vec{v}+\Delta v= (-vex+ v + Äv) \hat{i}
Applying the law of conservation of momentum, we get
(M + Äm) v = M(v + Äv) + Äm(-vex+ v + Äv)
After some cancellation we find
0 = MÄv + Äm(-vex + Äv)
If both Äv and Äm are small quantities relative to v and M, respectively, their product ,ÄvÄm, is negligible in comparison with the other terms, and we are left with
Äv = vex \frac{{\Delta m}}{M} (1)
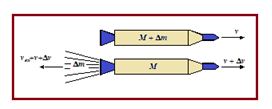
Since an increase in the mass of the expelled gases corresponds exactly to the loss in mass of the rocket system, we have Äm = -ÄM. In the limit as ÄM0 equation(1) becomes
dv= –vex \frac{{dM}}{M} On integrating both sides,
\int\limits_{{{{v}_{i}}}}^{{{{v}_{f}}}}{{dv}}=-\int\limits_{{{{M}_{i}}}}^{{{{M}_{f}}}}{{{{v}_{{ex}}}\frac{{dM}}{M}}}
we find
vf– vi= vexln \frac{{{{M}_{i}}}}{{{{M}_{f}}}} (2)
Illustration
The mass of a rocket is 2.8 x 106 kg at the launch time. Of this, 2 x 106 kg is fuel. The exhaust speed is 2500 m/s and the fuel is ejected at the rate of 1.4 x 104 kg/s.
(a) Find the thrust of the rocket
(b) What is its initial acceleration at launch time? Ignore air resistance.
Solution
(a) The magnitude of the thrust is given by
Thrust = vex \frac{{dM}}{{dt}} = (2500)(1.4 ´ 104) = 3.5 ´ 107 N
(b) Using equation
M\frac{{dv}}{{dt}}={{F}_{{ext}}}+{{v}_{{rel}}}\frac{{dM}}{{dt}}
We get the acceleration
a = \frac{{dv}}{{dt}}=\frac{{{{F}_{{ext}}}}}{M}+\frac{{{{v}_{{rel}}}}}{M}\frac{{dM}}{{dt}}
\frac{{dv}}{{dt}} = –g + \frac{1}{M} vex \frac{{dM}}{{dt}} = -9.8 + 12.5 = +2.7 m/s2
Illustration
A Chopper releases grain at a rate dm/dt onto a conveyor belt that moves at a constant speed v. What is the power of the motor driving the belt?

Let the system is some arbitrary length of belt whose mass we can call M. This mass of the system increases at the same rate that the grain falls,
so dM/dt= dm/dt.
Since the grain falls vertically, \displaystyle \vec{u}= 0 and \displaystyle {{\vec{v}}_{{rel}}}=\vec{u}-\vec{v}=-\vec{v}. Since the speed is constant,
dv/dt= 0. Thus from equation
\displaystyle 0={{\vec{F}}_{{ext}}},-\vec{v}\frac{{dm}}{{dt}}
Where \displaystyle {{\vec{F}}_{{ext}}} is the force needed to maintain constant speed because the mass is increasing. The power required \displaystyle (p=\vec{F}.\vec{v}) is
P = v2 \frac{{dm}}{{dt}}
It is interesting to compare this with the rate at which the kinetic energy of the grain increases.
\frac{{dK}}{{dt}} = \frac{d}{{dt}} \left( {\frac{1}{2}m{{v}^{2}}} \right) = \frac{1}{2}v2 \left( {\frac{{dm}}{{dt}}} \right)
This is only half the power input. The other half is dissipated as heat when the grain lands on the belt and slips relative to it.
Illustration
A uniform chain of mass m and length l hangs on a thread and touches the surface of a table by its lower end. Find the force exerted by the chain on the surface when half of its length has fallen on the table. The fallen part does not form heap.
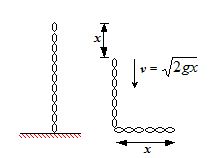
Solution
Let N be the normal reaction acting on the chain.
It consists of two parts
N = Nwt+ Nthrust
Nwt= \frac{m}{l}xg
Nthrust= vrel \frac{{dm}}{{dt}}
If v be the instantaneous velocity of the particle falling on the floor, then
vrel= v – 0 = v
\frac{{dm}}{{dt}}=\frac{{dm}}{{dx}}\frac{{dx}}{{dt}}
or \frac{{dm}}{{dt}}=v\left( {\frac{m}{l}} \right)
Thus Nth= {{v}^{2}}\left( {\frac{m}{l}} \right)
Since v = \sqrt{{2gx_{{}}^{{}}}}
Nth= \frac{{2mg}}{l}x
Total reaction is
N = \frac{{mgx}}{l}+\frac{{2mgx}}{l}
N = 3mg \left( {\frac{x}{l}} \right)
for x = l/2
N = \frac{3}{2}mg
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
Comprehension Based Question ( 1 And 2)
A bomb at rest explodes into two fragments of masses 3.0 kg and 1.0 kg. The total kinetic energy of the fragments is 6 × 104J. Calculate
1.
kinetic energy of the bigger fragment
(a) 3.0 × 104 J
(b) 1.5 × 104 J
(c) 1.2 × 104 J
(d) 1.5 × 10-4 J
Ans (b)
2.
momentum of the smaller fragment.
(a) 500 kgms–1
(b) 300 kgms–3
(c) 300 kgms–1
(d) –300 kgms–1
Ans (d)
3.
A man weighing 80 kg is standing on a trolley weighing 320 kg. The trolley is resting on frictionless horizontal rails. If the man starts walking on the trolley along the rails at speed 1 m/s then after 4s his displacement relative to the ground will be:
(a) 5 m
(b) 4.8 m
(c) 3.2 m
(d) 3.0 m
Ans (c)
4.
In a two block system an initial velocity v0 (with respect to ground) is given to block A:
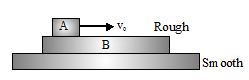
(a) the momentum of block A is not conserved
(b) the momentum of system of blocks A and B is conserved
(c) the increases in momentum of B is equal to the decrease in momentum block A
(d) all of the above
Ans (d)
5.
A uniform metal disc of radius R is taken and out of it a disc of diameter R is cut off from the end. The centre of mass of the remaining part will be:
(a) \frac{R}{4}\,\text{from}\,\,\text{the}\,\,\text{centre}
(b) \frac{R}{3}\text{from}\,\,\text{the}\,\,\text{centre}
(c) \frac{R}{5}\text{from}\,\,\text{the}\,\,\text{centre}
(d) \frac{R}{6}\text{from}\,\,\text{the}\,\,\text{centre}
Ans (d)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
1.
Two inclined surface of two movable smooth wedges of the same mass M are smoothly conjugated with the horizontal plane. A washer of mass m slides down the wedge from a height h. To what height (maximum) will the washer rise along the right wedge?
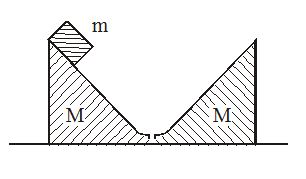
(a) h{{\left( {\frac{M}{{M-m}}} \right)}^{2}}
(b) h{{\left( {\frac{M}{{M-m}}} \right)}^{-2}}
(c) h{{\left( {\frac{M}{{M+m}}} \right)}^{2}}
(d) h{{\left( {\frac{M}{{M+m}}} \right)}^{3}}
Ans (c)
2.
A particle of mass 4m, which is at rest, explodes into three fragments. Two of the fragments each of mass m are found to move with speed v each in mutually perpendicular directions. Find the total energy released in the process of explosion.
(a) \frac{2}{3}m{{v}^{3}}
(b) \frac{3}{2}m{{v}^{-2}}
(c) \frac{3}{-2}m{{v}^{2}}
(d) \frac{3}{2}m{{v}^{2}}
Ans (d)
3.
A stationary U238 nucleus emits an a-particle (2He4) with velocity 1.4 × 107 m/s and kinetic energy 4.1 MeV. Calculate the velocity of the residual nucleus.
(a) –2.4 × 105 m/s
(b) 2.4 × 105 m/s
(c) 2.4 × 10-5 m/s
(d) 3.0 × 105 m/s
Ans (a)
4.
A boat with a man is moving near a dock. At a certain instant the boat is connected to a fixed point A on the shore by a rope. Initially the length of rope between the boat and point A is l1 = 25 m and the boat has velocity v1 = 5 m/s perpendicular to the rope. The man in the boat pulls the rope with a constant force F = 500 N to draw the boat near the dock. The boat and the man have a combined mass M = 200 kg. At the moment the length of the rope between the boat and point A is l2 = 20 m, find
(a)
the speed of the boat and
(a)7.50 m/s
(b)7.00 m/s
(c)7.22 m/s
(d)7.07 m/s
Ans (d)
(b)
the direction of motion of the boat with respect to the rope.
(resistance of water is negligible)
(a) \frac{6}{5}\sqrt{7}m/s at q = 62o
(b) \frac{5}{4}\sqrt{7}m/s at q = 62o
(c) \frac{3}{4}\sqrt{7}m/s at q = 62o
(d) \frac{-5}{4}\sqrt{7}m/s at q = 62o
Ans (b)
