Video Lecture
Theory For Making Notes
Circular Motion in a Vertical Plane
A particle of mass m is attached to a light and inextensible string. The other end of the string is fixed at O and the particle moves in a vertical circle of radius R equal to the length of the string as shown in the figure.
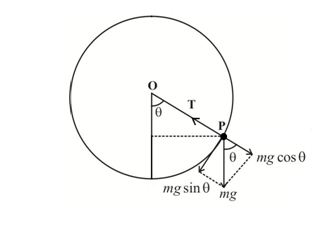
Consider the particle when it is at the point P and the string makes an angle θ with vertical. Forces acting on the particle are:
T = tension in the string along its length, and
mg = weight of the particle vertically downward.
Hence, net radial force on the particle is FR = T – mg cos θ
=> T – mgcos θ = mv2/R
=> T = mv2/R + mg cos θ ———–(1)
Since speed of the particle decreases with height, hence tension is maximum at the bottom most position, where θ =0
hence cos θ = 1 putting it in equation (1) we can find the maximum tension
Therefore Tmax = mv2/R + mg ( at the bottom )
Whereas tension is minimum at the highest position where θ = π. hence cos θ = -1 , putting it in equation (1) we can calculate the minimum tension
Hence Tmin = mv‘2/R – mg (at the top)
Here, v‘ = speed of the particle at the top.
Critical Velocity
It is the minimum velocity given to the particle at the lowest point to complete the circle.
The tendency of the string to slack is maximum when the particle is at the topmost point of the circle.
At the top, tension is given by
T = mv12/R – mg, where v1 = speed of the particle at the top.
If the string slacks at the highest point the body will leave the circular path hence the tension becomes zero. Lets’ calculate the velocity v1 at which tension becomes zero
T = mv12/R – mg putting T=0 we get
v1 = √gR
(this the minimum velocity that a body must have at the highest point in order to complete a vertical circle)
To achieve this velocity there must be a minimum velocity that the body must have at the lowest position called critical velocity ‘v’ . To calculate this critical velocity we must apply conservation of mechanical energy between uppermost and lowermost position.
KEbottom + PEbottom = KEtop + PEtop
1/2 mv2 + 0 = Mg(2R) + 1/2 mv12 … (2)
As v1 = √gR putting it in equation number (2)
We have 1/2 mv2 = 2mgR + 1/2 mgR
Thus we get
\displaystyle v=\,\sqrt{{5gR}}
In case of vertical circular motion this is the minimum velocity that a body must be given at the lowest position to complete a vertical circle
Note: In case the particle is attached with a light rod of length l, at the highest point its minimum velocity may be zero. Then, the critical velocity is 2√gl.
Illustration
A body slides down an inclined surface which ends into a vertical loop of radius R = 40 cm. What must be the height H of the inclined surface for the body not to fall at the uppermost point of the loop? Assume friction to be absent.
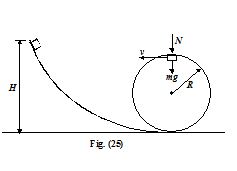
Solution
Let v be the velocity of the particle at the highest point.
According to Newton’s Second Law, the net force
Fnet = N + mg provides the centripetal force.
Therefore, N + mg = \frac{{m{{v}^{2}}}}{R}
The body is not detached from the loop if N ³ 0. In the limiting case, N = 0.
That is mg = \frac{{m{{v}^{2}}}}{R} or v2 = gR
Applying energy conservation at the initial and highest point of the loop, we get
mgH = mg(2R) + \frac{1}{2}m{{v}^{2}}
Using v2 = gR, we obtain,
mgH = mg(2R) + \frac{1}{2}m\left( {gR} \right)
or H = \frac{5}{2}R=2.5R
Putting R = 40 cm = 0.4 m, we get
H = (2.5) (0.4) = 1m.
Illustration
The bob of a simple pendulum of length L = 2 m has a mass m = 2 kg and a speed
v = 1 m/s when the string is at 35o to the vertical. Find the tension in the string at
(a) the lowest point in its swing
(b) the highest point
Solution
The problem requires to use dynamics and the conservation of mechanical energy. The forces on the bob are shown in the figure.
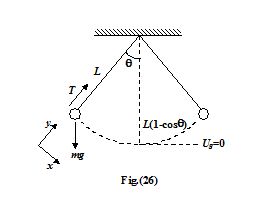
The acceleration has both radial and tangential components.
The equation for tangential component, ∑Fx = mg sinθ = ma
Since the bob is moving in a circular path of radius L, the equation for the radial component is
∑Fy = T – mg cosq = \frac{{m{{v}^{2}}}}{L} …(i)
To find the tension we need the speed, which can be found from the conservation law. We set Ug = 0 at the lowest point.
Note that the height is y = L – L cosθ. The mechanical energy is
E = \frac{1}{2}m{{v}^{2}}+mgL\left( {1-\cos \theta } \right) …(ii)
= \frac{1}{2} (2kg)(1 m/s)2 + (2kg)(9.8 N/kg)(2m)(1 – 0.8) = 9 J
(a) At the lowest point θ = 0; hence (ii) becomes
E = \frac{1}{2}mv_{{\max }}^{2}+ 0
Since E = 9 J we find vmax = 3 m/s.
Now we have the speed we can find the tension at θ = 0. From (i), T – mg = \frac{{mv_{{\max }}^{2}}}{L}, from which we find
T = 20 + 9 = 29 N
(b) At the highest point v = 0; hence, (ii) becomes
E = 0 + mgL(1 – cosθmax)
Using E = 9 J lead to cosθmax = \frac{{31}}{{40}}
Since v = 0, therefore, T = mgcosθmax = 15.5 N
Illustration
A mass ‘m’ is revolving in a vertical circle at the end of a string of length 20 cm. By how much does the tension of the string at the lowest point exceed the tension at the topmost point?
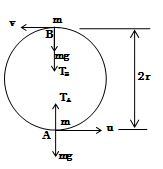
(A) 2 mg (B) 4 mg
(C) 6 mg (D) 8 mg
Solution
At the lowest point A
\displaystyle {{T}_{A}}-mg=\frac{{m{{u}^{2}}}}{r} …(1)
At the highest point B
\displaystyle {{T}_{B}}+mg=\frac{{m{{v}^{2}}}}{r} …(2)
Gain in PE from A to B = 2mgr = loss in KE
2 mgr = (1/2) m(u2 – v2)
u2 – v2 = 4gr …(3)
From (1), (2) and (3)
\displaystyle {{T}_{A}}-{{T}_{B}}-2mg=\frac{m}{r}\left( {{{u}^{2}}-{{v}^{2}}} \right)
\displaystyle {{T}_{A}}-{{T}_{B}}=2mg+\frac{m}{r}\times 4gr=6\ mg
∴ Option (c) Is The Correct Answer.
Illustration
A point mass m starts from rest and slides down the surface of a fixed frictionless solid hemisphere of radius R as shown in figure. Measure angles from the vertical and potential energy from the top. Find
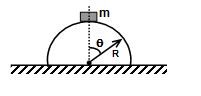
(a) the change in potential energy of the mass with angle
(b) the kinetic energy as a function of angle,
(c) the radial and tangential acceleration as a function of angle,
Solution
(a)
Consider the mass when it is at the point B.
UA (P.E. at A) = 0
UB(P.E. at B)= -mgR (1 – cosθ)
ΔU = UB – UA
ΔU = – mgR(1 – cosθ)
Negative sign indicates that P.E. decreases as particle slides down.
(b)
Conserving energy at points A and B.
UA + TA = UB + TB
where UA = P.E. at A, UB = P.E. at B
TA = K.E. at A, TB = K.E. at B
0 + 0 = -mgR(1- cosθ) + TB
T = mgR(1 – cosθ)
(c)
Since T = \displaystyle \frac{1}{2}m{{v}^{2}}
\displaystyle \frac{1}{2}m{{v}^{2}} = mgR(1 – cosθ) = 2mgR sin2(θ/2)
v = \displaystyle 2\sqrt{{gR}} sin(q/2) ∴ ar = v2/R
ar = 4g sin2(θ/2) As at = \frac{{dv}}{{dt}}
at = √(gR) cos(θ/2) \displaystyle \frac{{d\theta }}{{dt}}
= √(gR) wcos(θ/2)
at = √(g/R) v cos (θ/2) , as ωR = v
Practice Questions (Basic Level)
Q.1
The tube AC forms a quarter circle in a vertical plane. The ball B has an area of cross-section slightly smaller than that of the tube, and can move without friction through it. B is placed at A and displaced slightly. It will
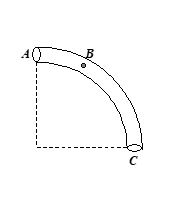
(a) always be in contact with the inner wall of the tube
(b) always be in contact with the outer wall of the tube
(c) initially be in contact with the inner wall and later with the outer wall
(d) initially be in contact with the outer wall and later with the inner wall
Ans. (c)
Practice Questions (JEE Main Level)
Q.1
A particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be
(a) zero
(b) \sqrt{{gl}}
(c) \sqrt{{1.5gl}}
(d) \sqrt{{2gl}}
Ans. (a)
Q.2
A stone tied to a string of length L is whirled in a vertical circle, with the other end of the string at the centre. At a certain instant of time, the stone is at its lower position and has a speed u. The magnitude of the change in its velocity as it reaches a position where the string is horizontal is
(a) \sqrt{{{{u}^{2}}-2gL}}
(b) \sqrt{{2gL}}
(c) \sqrt{{{{u}^{2}}-gL}}
(d) \sqrt{{2\left( {{{u}^{2}}-gL} \right)}}
Ans. (d)
Q.3
A particle is placed at the highest point of a frictionless hemispherical surface. If the particle is allowed to slide down, the angular displacement q at which it will leave the surface is
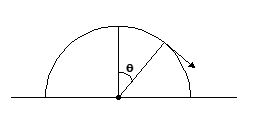
(a) cos-1(1/3)
(b) cos-1(1/2)
(c) cos-1(2/3)
(d) cos-2(3/4)
Ans. (c)
Practice Questions (JEE Advance Level)
Q.1
A small spherical ball is suspended through a string of length l. The whole arrangement is placed in a vehicle which is moving with velocity v. Now suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then
(a) v=\sqrt{{5gl}}
(b) v=\sqrt{{10gl}}
(c) velocity of the ball at highest point is \sqrt{{gl}}
(d) velocity of the ball at the highest point is \sqrt{{3gl}}
Ans. (d)
Q.2
A simple pendulum has a bob of mass m and swings with an angular amplitude f. The tension in the thread is T. At a certain time, the string makes an angle q with the vertical
(q £ f). Choose the incorrect option regarding tension T
(a) T = mg cosq, for all values of q
(b) T = mg cosq, only for q = f
(c) T = mg, for q = {{\cos }^{{-1}}}\left[ {\frac{1}{3}\left( {2\cos \varphi +1} \right)} \right]
(d) T will be larger for smaller values of q
Ans. (a)

