Video Lecture
Theory For Making Notes
Dynamics of Circular Motion
A body moving with constant speed in a circular path is continuously accelerated towards the centre of rotation. The magnitude of acceleration is given by
a=\frac{{{{v}^{2}}}}{r}={{\omega }^{2}}r
where v is the constant speed \left( {v=\omega r} \right) and
r is the radius of the circular path.
According to Newton’s Second Law, a body moving in a circular path with constant speed must be acted upon by an unbalanced force which is always directed towards the centre. This necessary unbalanced force is called the centripetal force.
F=\frac{{m{{v}^{2}}}}{r}=m{{\omega }^{2}}r
A body moving with constant speed in a circle is not in equilibrium.
It should be remembered that in the absence of the centripetal force the body will move in a straight line with constant speed.
It is not a new kind of force which acts on bodies. In fact, any force which is directed towards the centre may provide the necessary centripetal force.
For example
- when a stone tied with a string is rotated in a circular path, the tension in the string provides the centripetal force.
- when a car negotiates a curve the force of friction between the tyres and the road provide the necessary centripetal force.
- the gravitational force of attraction between the sun and a planet provides the centripetal force.
- the electric force of attraction between the nucleus and the revolving electron provides the centripetal force in an atom.
Centripetal and Centrifugal force
Consider a block which is tied to the centre post of a rotating platform by a string. Now the cofusion of students is when to use the centripetal force and when centrifugal force.
For understanding this concept consider two observers one standing on the ground called inertial frame and the other standing on the rotating plateform and is in circular motion called non inertial frame.
From the perspective of inertial frame
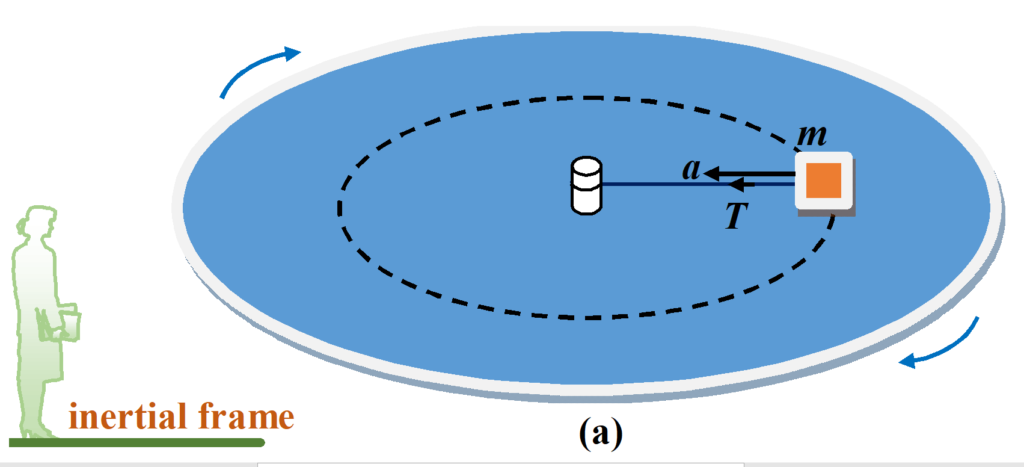
An inertial observer sees the block moving in a circle and hence the observer consider a centripetal force on the block and applies newton’s second law and say that tension T is providing centripetal force to the block.
Therefore \displaystyle T= \frac{{m{{v}^{2}}}}{r}\,
From the perspective of non inertial frame
According to a non inertial observer on the platform, the circular motion of the block is not visible but it appears at rest . At the same time the non inertial frame apply a pseudo force on the block. This pseudo force is nothing but the centrifugal force that acts on the block radially outwards.
Centrifugal force is a pseudo force which is experienced by the occupants of non-inertial frames moving in a circular path with constant speed. Its magnitude is equal to that of the centripetal force but its direction is exactly opposite to that.
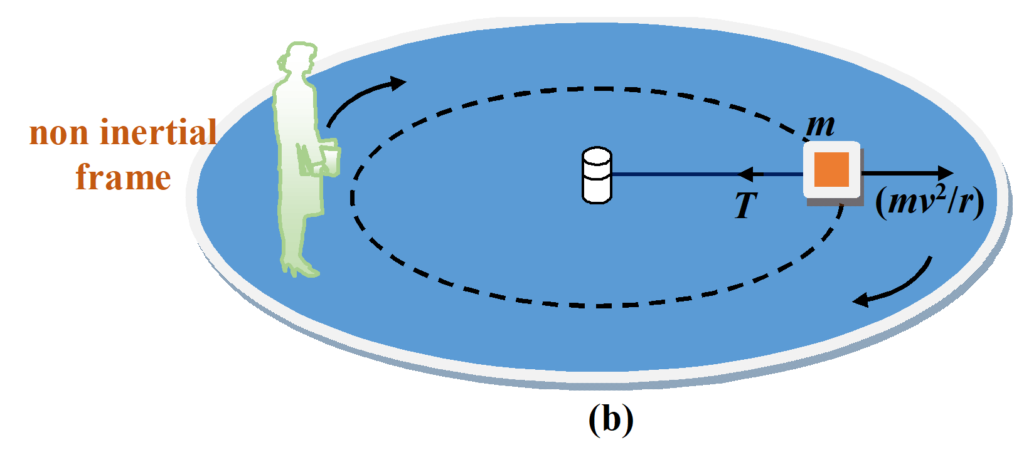
Hence the non inertial observer will say that under the action of two forces that is tension and centrifugal force the block is at rest hence he will balance the outward and inward forces acting on the block. So according to him the equation will be given by \displaystyle T= \frac{{m{{v}^{2}}}}{r}\,
Note that for inertial frame the block is in circular motion and for non inertial frame the block is at rest . Their observations and explanations are different but final equation from inertial and non inertial frame comes out to be same.
Motion of a car on a circular level road
Consider a car of weight mg going around on a circular turn of radius r with constant velocity v on a level road as shown in following figure.
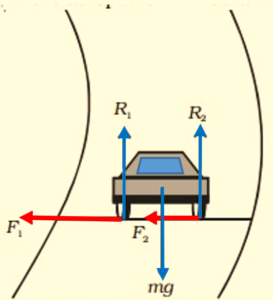
While taking the round, the tyres of the car tend to leave the road and move away from the centre of curve. Hence the forces of friction f1 and f2 will act inward at the inner and the outer tyres respectively. If R1 and R2 are the normal reactions of ground on the tyres, then
\displaystyle {{f}_{1}}={{\mu }_{s}}{{R}_{1}} and \displaystyle {{f}_{2}}={{\mu }_{s}}{{R}_{2}}
Where \displaystyle {{\mu }_{s}} is the coefficient of static friction between the tyre and the road
Hence, total frictional force
\displaystyle f={{\mu }_{s}}{{R}_{1}}+{{\mu }_{s}}{{R}_{2}}={{\mu }_{s}}({{R}_{1}}+{{R}_{2}})={{\mu }_{s}}R
Where R is the reaction of the ground on the car.
Because the total frictional force f cannot exceed μsR, therefore we may write
\displaystyle f\le {{\mu }_{s}}R
This frictional force will provide the necessary centripetal force f i.e., \displaystyle f=\frac{{m{{v}^{2}}}}{r}
Hence, \displaystyle \frac{{m{{v}^{2}}}}{r}\le {{\mu }_{s}}R ….(i)
As total normal reaction balances the weight of the car, hence R = mg …..(ii)
From equation (i) and (ii), we get
\displaystyle \frac{{m{{v}^{2}}}}{r}\le {{\mu }_{s}mg}
or \displaystyle {{v}^{2}}\le {{\mu }_{s}}rg
or \displaystyle v\le \sqrt{{{{\mu }_{s}}rg}}
Therefore, the maximum velocity ( \displaystyle {{V}_{{\max }}}) with which a car can travel on level curved road is given by \displaystyle {{V}_{{\max }}}\,=\,\sqrt{{\left( {{{\mu }_{s}}rg} \right)}}
If the car is driven at a speed greater than \displaystyle {{V}_{{\max }}}, then the car will skip and go off the road in a circle of radius greater than r. This is because even the maximum available friction will be in adequate to provide the necessary centripetal force.
Motion Of Vehicle on a curved banked road
Friction is not always reliable at circular turns if high speeds and sharp turns are involved. To avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is somewhat lifted up as compared to the inner part.
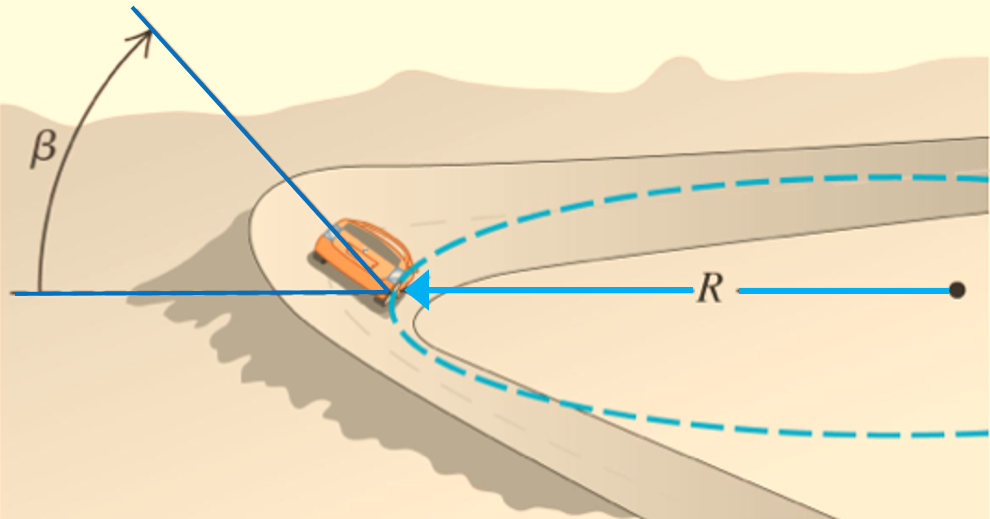
The surface of road and hence, even the normal force of contact make an angle q with horizontal and vertical respectively. The various forces acting on the body are shown in the figure given below A.At high speed the car has a tendency to skid upward so friction acts along the plane downward .Resolving the forces into two components along x axis and y axis.
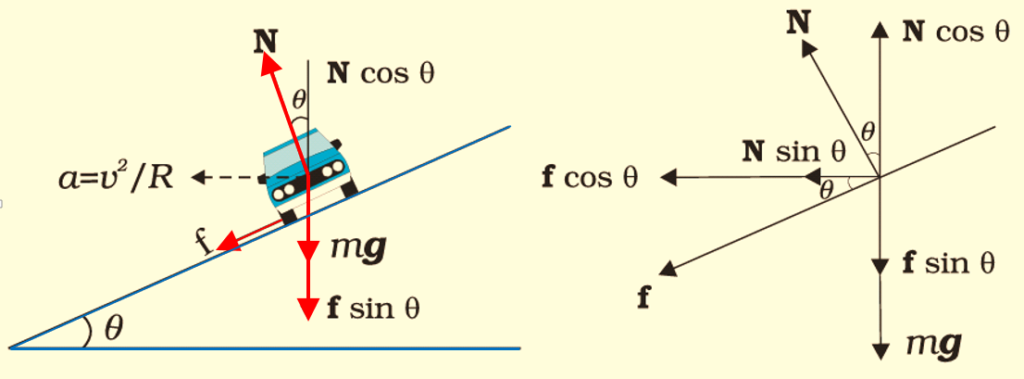
Hence
\displaystyle mg+f\sin \theta =N\cos \theta ( where \displaystyle f=\mu N)
Hence, \displaystyle mg=N\cos \theta -\mu N\sin \theta …(i)
\displaystyle \frac{{m{{v}^{2}}}}{r}\,=\,N\,\,\sin \,\theta \,+\,\mu \,N\,\,\cos \,\theta …(ii)
Divide (ii) by (i)
\displaystyle \frac{{{{v}^{2}}}}{{rg}}\,=\,\frac{{\sin \,\theta \,+\,\mu \,\cos \,\theta }}{{\cos \,\theta \,-\,\mu \,\sin \,\theta }}
\displaystyle \therefore v=\sqrt{{rg\left( {\frac{{\tan \theta +\mu }}{{1-\mu \tan \theta }}} \right)}}
If the speed of the car increases above v then the car skids up the plane.
Optimum Speed
The speed at which the wear and tear of the tyres of car is minimum called optimum speed. At this speed no friction acts side wise on the car.
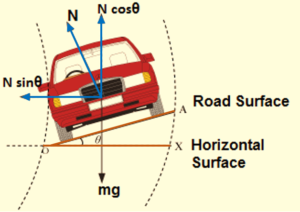
\displaystyle \frac{{m{{v}^{2}}}}{r}\,=\,N\,\sin \,\theta …(i)
\displaystyle mg\,=\,N\,\cos \,\theta …(ii)
Dividing equation (1) by (2)
\displaystyle \frac{{{{v}^{2}}}}{{rg}}\,=\,\tan \,\theta
Hence
\displaystyle v\,=\,\sqrt{{r\,\,g\,\tan \,\theta }}
Conical Pendulum
This is the example of uniform circular motion in horizontal plane.
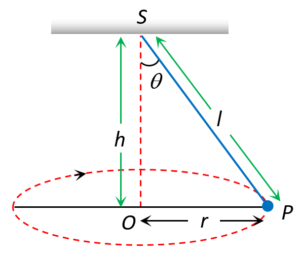
A bob of mass m attached to a light and in-extensible string rotates in a horizontal circle of radius r with constant angular speed w about the vertical. The string makes angle q with vertical and appears tracing the surface of a cone. So this arrangement is called conical pendulum.
The force acting on the bob are tension and weight of the bob.
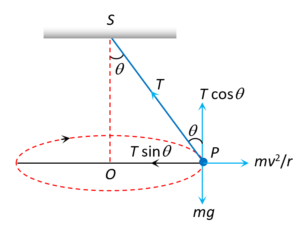
From the figure T\sin \theta =\frac{{m{{v}^{2}}}}{r} ….(i)
and T\cos \theta =mg ….(ii)
squaring and adding equation (i) and (ii) gives tension T
Tension in the string : T=mg\sqrt{{1+{{{\left( {\frac{{{{v}^{2}}}}{{rg}}} \right)}}^{2}}}}
From equation (ii)
T=\frac{{mg}}{{\cos \theta }}=\frac{{mgl}}{{\sqrt{{{{l}^{2}}-{{r}^{2}}}}}} [As \cos \theta =\frac{h}{l}=\frac{{\sqrt{{{{l}^{2}}-{{r}^{2}}}}}}{l}]
On dividing equation (i) and (ii) the angle of string with the vertical can be found as
\tan \theta =\frac{{{{v}^{2}}}}{{rg}}
hence v=\sqrt{{gr\tan \theta }}
Angular velocity of the bob \omega :
\omega ={\frac{v}{r}}=\sqrt{{\frac{g}{r}\tan \theta }}=\sqrt{{\frac{g}{h}}}=\sqrt{{\frac{g}{{l\cos \theta }}}} [As \tan \theta =\frac{r}{h} and \cos \theta =\frac{h}{l}]
Time period of revolution :
T={\frac{2\pi}{\omega}}=2\pi \sqrt{{\frac{{l\cos \theta }}{g}}}=2\pi \sqrt{{\frac{h}{g}}}.
Bending Of Cyclist on a circular turn
A cyclist provides himself the necessary centripetal force by leaning inward on a horizontal track, while going round a curve. Consider a cyclist of weight mg taking a turn of radius r with velocity v. In order to provide the necessary centripetal force, the cyclist leans through angle \theta inwards as shown in figure.
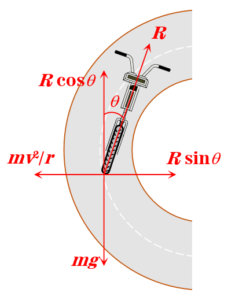
The cyclist is under the action of the following forces :
(i) The weight mg acting vertically downward at the centre of gravity of cycle and the cyclist.
(ii) The reaction R of the ground on cyclist. It will act along a line-making angle \theta with the vertical.
The vertical component R\cos\theta of the normal reaction R will balance the weight of the cyclist, while the horizontal component R\sin\theta will provide the necessary centripetal force to the cyclist.
R\sin \theta =\frac{{m{{v}^{2}}}}{r} …(i)
and R\cos\theta=mg …(ii)
Dividing equation (i) by (ii), we have
\frac{{R\sin \theta }}{{R\cos \theta }}=\frac{{m{{{{v}^{2}}}}/{r}\;}}{{mg}}
or \tan \theta =\frac{{{{v}^{2}}}}{{rg}} …(iii)
Therefore, the cyclist should bend through an angle \theta ={{\tan }^{{-1}}}\left( {\frac{{{{v}^{2}}}}{{rg}}} \right)
It follows that the angle through which cyclist should bend will be greater, if
(i) The radius of the curve is small i.e. the curve is sharper
(ii) The velocity of the cyclist is large.
For the same reasons, an ice skater or an aeroplane has to bend inwards, while taking a turn.
Practice Questions (Basic Level)
1.
A car of mass M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
(a) The acceleration of the car is towards the centre of the path.
(b) The magnitude of the frictional force on the car is greater than \displaystyle \frac{{m{{v}^{2}}}}{r}.
(c) The friction coefficient between the ground and the car is not less than \frac{a}{g}.
(d) Both (b) and (c)
Ans. (d)
2.
A block of mass \displaystyle \frac{1}{{{{\pi }^{2}}}} kg is constrained to move in a circular path and makes one revolution in 1s. It is attached to the centre of circle by a light spring of spring constant 5N/m and natural length 1m. The radius of the circular path is
(a) \frac{1}{4} m
(b) 1.25 m
(c) 2.5 m
(d) 1.5 m
Ans. (b)
3.
A cyclist speeding at 18 km/hr on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The co-efficient of static friction between the tyres and the road is 0.1. Will the cyclist slip while taking the turn?
(a)Yes,The cyclist will slip while taking the circular turn.
(b)No,The cyclist will not slip while taking the circular turn.
(c)May slip depending upon his angle with the vertical
(d) none
Ans (a)
Question ( 4 And 5)
A circular racetrack of radius 300 m is banked at an angle of 15o. If the coefficient of friction between the wheels of race car and the road is 0.2, what is the (tan15 = 0.27)
4.
(a) optimum speed of the racecar to avoid wear and tear on its tyres
(a)10.00 m/s
(b)20.5 m/s
(c)28.4 m/s
(d)25.6 m/s
Ans (c)
5.
Maximum permissible speed to avoid slipping?
(a)35.0 m/s
(b) 36.8 m/s
(c)38.6 m/s
(d)40.0 m/s
Ans (c)
6.
A stone tied to a string is rotated in a circle. If the string is cut, the stone flies away from the circle because
(a) A centrifugal force acts on the stone
(b) A centripetal force acts on the stone
(c) Of its inertia
(d) Reaction of the centripetal force
Ans (c)
7.
A motor cyclist moving with a velocity of 72 km/hour on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20 meters. The acceleration due to gravity is 10 m/sec2. In order to avoid skidding, he must not bend with respect to the vertical plane by an angle greater than
(a) \theta ={{\tan }^{{-1}}}6
(b) \theta ={{\tan }^{{-1}}}2
(c) \theta ={{\tan }^{{-1}}}3
(d) \theta ={{\tan }^{{-1}}}7
Ans (b)
8.
Two masses m and M are attached at the opposite ends A and B of a string AOB of length L.The system is made to rotate about a vertical axis passing through O on a horizontal frictionless surface with an angular velocity \omega. Find OB such that the tension in part OA and OB is same.
(a) OB=\frac{{mL}}{{M+m}}
(b) OB=\frac{{ML}}{{M+m}}
(c) OB=\frac{{mML}}{{M+m}}
(d) OB=\frac{{2mL}}{{M+m}}
Ans (a)
9.
Radius of the curved road on national highway is R. Width of the road is b. The outer edge of the road is raised by a small height h with respect to inner edge so that a car with velocity v can pass safe over it. The value of h is
(a) \frac{{{{v}}R}}{{bg}}
(b) \frac{{{{v}^{2}}R}}{{bg}}
(c) \frac{{{{v}}b}}{{Rg}^{2}}
(d) \frac{{{{v}^{2}}b}}{{Rg}}
Ans (d)
10.
A ball of mass 0.1 is whirled in a horizontal circle of radius 1 m. by means of a string at an initial speed of 10 R.P.M. Keeping the radius constant, the tension in the string is reduced to one quarter of its initial value. The new speed is
(a) 5 r.p.m.
(b) 10 r.p.m.
(c) 20 r.p.m.
(d) 14 r.p.m.
Ans (a)
Practice Questions (JEE Main Level)
1.
A block of mass {m}_{1} is attached to a cord of length {L}_{1} which is fixed at one end. The mass moves in a horizontal circle on a frictionless table. A second block of mass {m}_{2} is attached to the first mass {m}_{1} by a cord of length {L}_{2} and also moves in a circle, as shown in the figure. If the angular speed is {\omega}, find the tension in each cord.
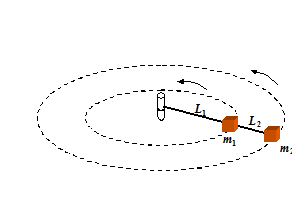
(a) \displaystyle {{T}_{2}}={{m}_{2}}({{L}_{1}}+{{L}_{2}}){{\omega }^{2}}\text{ , }{{T}_{1}}={{m}_{2}}({{L}_{1}}+{{L}_{2}}){{\omega }^{2}}\text{ +}{{m}_{1}}{{L}_{1}}{{\omega }^{2}}
(b) \displaystyle {{T}_{2}}={{m}_{1}}({{L}_{1}}+{{L}_{2}}){{\omega }^{2}}\text{ , }{{T}_{1}}={{m}_{1}}({{L}_{1}}+{{L}_{2}}){{\omega }^{2}}\text{ +}{{m}_{2}}{{L}_{1}}{{\omega }^{2}}
(c) \displaystyle {{T}_{2}}={2{m}_{1}}({{L}_{1}}-{{L}_{2}}){{\omega }}\text{ , }{{T}_{1}}={2{m}_{1}}({{L}_{1}}-{{L}_{2}}){{\omega }}\text{ +}{2{m}_{2}}{{L}_{1}}{{\omega }^{2}}
(d) \displaystyle {{T}_{2}}={{{m}_{1}}^{2}}({{L}_{1}}-{{L}_{2}}){{\omega }}\text{ , }{{T}_{1}}={2{m}_{1}}({{L}_{1}}-{{L}_{2}}){{\omega }^{2}}\text{ +}{2{m}_{2}}{{L}_{1}}{{\omega }}
Ans (a)
2.
A mass m on a frictionless table is attached to a hanging mass M by a string through a hole in the surface as shown in the figure. Find the linear speed with which m must move in order for Mto stay at rest.
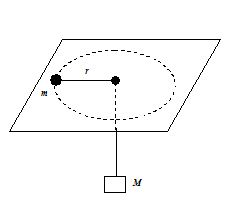
(a)\sqrt{{\frac{{Mg}}{m}}}
(b)\sqrt{{\frac{{Mgr}}{m}}}
(c)\sqrt{{\frac{{Mgr}}{2m}}}
(d)\sqrt{{\frac{{2Mgr}}{m}}}
Ans (b)
3.
A block of mass 0.4 kg is attached to a vertical rotating spindle by two strings of equal length, as shown in the figure. The time period of rotation is 1.2 s. Determine the tensions in the strings.
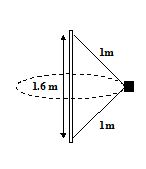
(a) 2 N, 5 N
(b) 8 N, 3 N
(c) 5 N, 3 N
(d) 1 N, 5 N
Ans (b)
4.
A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity {{\omega }_{0}}. If the length of the string and angular velocity are doubled, the tension in the string which was initially {{T }_{0}} is now
(a) {{T }_{0}}
(b) \frac {{T }_{0}}{2}
(c) {4{T }_{0}}
(d) {8{T }_{0}}
Ans (d)
5.
Three identical particles are joined together by a thread at A,B and C as shown in figure. All the three particles are rotated with an angular velocity \omega in a horizontal plane, then the ratio of tensions in the three sections BC, AB and OA of the string is
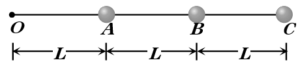
(a) 3 : 5 : 7
(b) 3 : 4 : 5
(c) 7 : 11 : 6
(d) 3 : 5 : 6
Ans (d)
6.
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/sec. A plumb bob is suspended from the roof of the car by a light rigid rod of length 1.00 m. The angle made by the rod with track is
(a) {0}^o
(b) {60}^o
(c) {45}^o
(d) {30}^o
Ans (c)
7.
Choose the incorrect statement
(a) When an automobile while going too fast around a curve overturns, its inner wheels leave the ground first.
(b) Two similar trains are moving along the equatorial line with the same speed but in opposite direction. They will exert equal pressure on the rails.
(c) Centripetal and centrifugal forces don’t act at the same time.
(d) Improper banking of roads causes wear and tear of tyres.
Ans (b)
Practice Questions (JEE Advance Level)
1.
A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The co-efficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
(a)1.4 s-1
(b) 2.5 s-1
(c)3.0 s-1
(d)4.7 s-1
Ans(d)
2.
An automobile enters a turn whose radius is R. The road is banked at angle {\theta}, and the coefficent of friction between wheels and road is {\mu}. Find the maximum and minimum speeds for the car to stay on the road without skidding sidways.
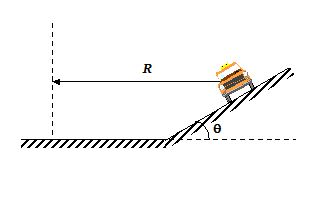
(a)vmin= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,-\,\mu \,\cos \theta }}{{\cos \theta \,+\,\mu \,\sin \theta }}} \right)}}; vmax= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,\mu \,\cos \theta }}{{\cos \theta \,-\,\mu \,\sin \theta }}} \right)}}
(b)vmin= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,\mu \,\cos \theta }}{{\cos \theta \,+\,\mu \,\sin \theta }}} \right)}}; vmax= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,-\,\mu \,\cos \theta }}{{\cos \theta \,-\,\mu \,\sin \theta }}} \right)}}
(c)vmin= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,\mu \,\cos \theta }}{{\cos \theta \,-\,\mu \,\sin \theta }}} \right)}}; vmax= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,\mu \,\cos \theta }}{{\cos \theta \,-\,\mu \,\sin \theta }}} \right)}}
(d)vmin= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,\mu \,\cos \theta }}{{\cos \theta \,-\,\mu \,\sin \theta }}} \right)}}; vmax= \sqrt{{Rg\,\left( {\frac{{\sin \theta \,+\,{{\mu}^{2}} \,\cos \theta }}{{\cos \theta \,+\,\mu \,\sin \theta }}} \right)}}
Ans(a)
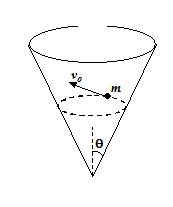
3.
A particle of mass m slides without friction on the inside of a cone. The axis of the cone is vertical, and gravity is directed downward. The apex half-angle of the cone is {\theta}, as shown. The path of the particle happens to be a circle in a horizontal plane. The speed of the particle is {{v}_{o}}. Then the radius of the circular path is.
(a)\frac{{v_{o}^{3}}}{g}\tan \theta
(b)\frac{{v_{o}}}{g}\cot \theta
(c)\frac{{v_{o}^{2}}}{g}\tan \theta
(d)\frac{{v_{o}^{2}}}{g}\cot \theta
Ans(c)
Question ( 4 to 6)
Two blocks of masses m1 = 10 kg and m2 = 5 kg, connected to each other by a massless inextensible string of length 0.3 m, are placed along a diameter of turn table. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. The table is rotating with an angular velocity of 10 rad/s about a vertical axis passing through its centreO. The masses are placed along the diameter of the table on either side of the centre O such that the mass m1 is at a distance of 0.124 m from O. The masses are observed to be at rest with respect to an observer on the turn table.
4.
Calculate the frictional force on m1.
(a)33 N
(b)30 N
(c)40 N
(d) 36 N
Ans (d)
5.
What should be the minimum angular speed of the turn table so that the masses will slip from this position?
(a)12.37 rad/s
(b)11.7 rad/s
(c) 14.15 rad/s
(d)9.25 rad/s
Ans(b)
6
How should the masses be placed with the string remaining taut, so that there is no frictional force acting on the mass m Take g = 10 m/s2.
(a)0 m and 0 m
(b)0.1 m and 0.2 m
(c)0.3 m and 0.5 m
(d)1 m and 2 m
Ans(b)
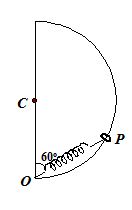
7.
A smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length (3R/4) is attached to the lower point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held stationary at the point P such that the spring makes an angle of 60o with the vertical. The spring constant k = mg/R.Consider the instant when the ring is released and determine the tangential acceleration of the ring and the normal reaction.
(a)\frac{{4\sqrt{3}}}{9}g, (3/7)mg
(b)\frac{{5\sqrt{3}}}{8}g, (3/8)mg
(c)\frac{{2\sqrt{6}}}{3}g, (5/8)mg
(d)\frac{{3\sqrt{2}}}{2}g, (1/8)mg
Ans(b)
8.
A toy car of mass m can travel at a fixed speed. It moves in a circle on a horizontal table. The centripetal force is provided by a string attached to a block of mass M that hangs as shown in the figure. The coefficient of static friction is µ. Then ratio of the maximum radius to the minimum radius possible is
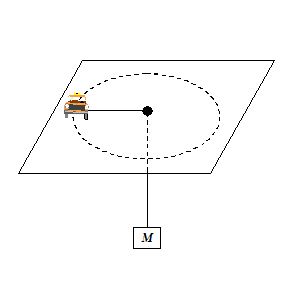
(a) \frac{{M\,-\,{\mu} m}}{{M\,+\,2{\mu} m}}
(b) \frac{{M\,-\,\mu m}}{{M\,+\,\mu m}}
(c) \frac{{M\,+\,\mu m}}{{M\,-\,\mu m}}
(d) \frac{{M\,+\,2{\mu} m}}{{M\,-\,{\mu} m}}
Ans (c)
Question (9 and 10)
In the figure shown, if the system is rotated in horizontal circle with angular velocity w,
Given m1 = 10 kg, m2 = 5 kg, R = 10 m and g = 10 m/s2.
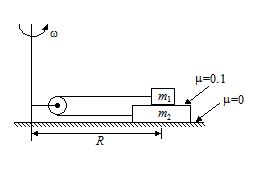
9.
calculate the minimum value of w to start relative motion between the two blocks, and
(a) 0.63 rad/s
(b) 0.50 rad/s
(c) 0.25 rad/s
(d) 0.70 rad/s
Ans (a)
10.
calculate the tension in the string connecting m1 and m2 when slipping just starts between the blocks.
(a) 100 N
(b) 60 N
(c) 30 N
(d) 50 N
Ans (c)


