Video Lecture
Theory For Making Notes
Centre of mass
It is a point inside or outside of a body where the whole mass of the body is suppose to be concentrated. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion.The centre of mass of a body or a system of bodies is the point that moves as through all of the mass were concentrated there.This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. This may also be defined as a point where the body can be balanced by simply giving a support at this point.
The centre of mass of a bat lies along the bat’s central axis. One can locate it by balancing the bat horizontally on an outstretched finger or any small support as shown in the figure. The centre of mass is on the bat’s axis just above the finger or support.

Location Of Centre of mass
For a system of n particles whose position vectors are \displaystyle {{\vec{r}}_{1}},{{\vec{r}}_{2}},………{{\vec{r}}_{n}} as shown in the figure,
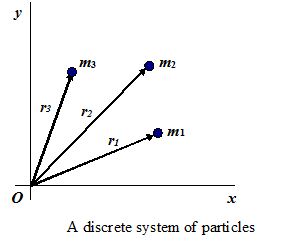
the position vector for the center of mass {{\text{vec{ r}}}_{{\text{cm}}}} is defined as
\displaystyle {{\vec{r}}_{{cm}}}=\frac{{{{m}_{1}}{{{\vec{r}}}_{1}}+{{m}_{2}}{{{\vec{r}}}_{2}}+……+{{m}_{n}}{{{\vec{r}}}_{n}}}}{{{{m}_{1}}+{{m}_{2}}+……+{{m}_{n}}}} —(1)
Or \displaystyle {{\vec{r}}_{{cm}}}=\sum{{\frac{{{{m}_{i}}{{{\vec{r}}}_{i}}}}{M}}}
where \overrightarrow{{{{r}_{1}}}}={{x}_{i}}\hat{i}+{{y}_{i}}\hat{j}+{{z}_{i}}\hat{k}. and {{\overrightarrow{{r\,}}}_{{\mathbf{CM}}}}={{x}_{{\mathbf{CM}}}}\,\hat{i}+\ {{y}_{{\mathbf{CM}}}}\,\hat{j}+{{z}_{{\mathbf{CM}}}}\,\hat{k}.
where M = ∑mi is the total mass of the system.
The components ofequation (1) are defined as
{{x}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{x}_{i}}}},\ \,\,{{y}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{y}_{i}}}},\ \,{{z}_{{\mathbf{CM}}}}=\frac{1}{M}\sum\limits_{{i=1}}^{n}{{{{m}_{i}}{{z}_{i}}}},
For locating center of mass of a continuous distribution of mass like 3D bodies etc.
We can write, {{x}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{x\,dm}} , {{y}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{y\,dm}} , {{z}_{{\mathbf{CM}}}}=\frac{1}{M}\int{{z\,dm}}
For derivation part please see the video lectures
Certain Important Points Related To Centre of mass
(1)
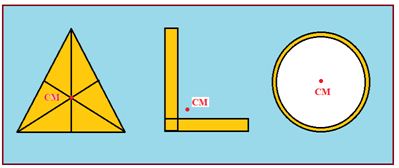
There may or may not be any mass present physically at centre of mass.
(2)
It may be within or outside the body.
(3)
Its position depends on the shape of the body.
(4)
For a given shape it depends on the distribution of mass within the body and is closer to massive part.
(5)
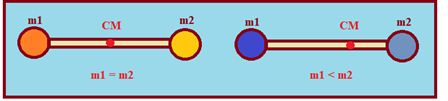
For symmetrical bodies having homogeneous distribution of mass it coincides with centre of symmetry or geometrical centre.
Symmetry can give an idea to locate the position of center of mass
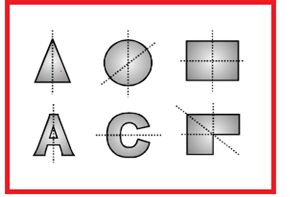
The center of mass of the above sheets will lie on the dotted line shown.
(6)
If we know the centre of mass of parts of the system and their masses, we can get the combined centre of mass by treating the parts as point particles placed at their respective centre of masses.
(7)
It is independent of the co-ordinate system, e.g., the centre of mass, i.e., {{\overrightarrow{{R\,}}}_{{CM}}}=0, then by definition (1/M)\sum{{{{m}_{i}}}}\,\overrightarrow{{{{r}_{i}}}}=0 or \sum{{{{m}_{i}}}}\,\overrightarrow{{{{r}_{i}}}}=0 .
i.e., the sum of the moments of the masses of a system about its centre of mass is always zero.
Are centre of mass and centre of gravity, two words for one and the same point?
No, centre of mass of a body is defined as the point at which the whole of its mass is supposed to be concentrated while centre of gravity of a body is defined as the point at which whole of its weight is supposed to be concentrated.
Illustration
Calculate the position of centre of mass of a system consisting of two particles of masses m1 and m2 separated by a distance L apart, from m1.
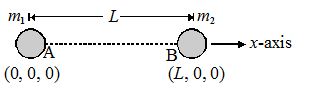
Solution
Treating the line joining the two particles as x-axis, and m1 at the origin, the co-ordinates of the two particles will be (0, 0, 0) and (L, 0, 0). So,
{{X}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}L}}{{{{m}_{1}}+{{m}_{2}}}};\ \,\,\,{{X}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}\times 0}}{{{{m}_{1}}+{{m}_{2}}}}\ \,\,\,\text{and}\ \,\,{{Z}_{{CM}}}=\frac{{{{m}_{1}}\times 0+{{m}_{2}}\times 0}}{{{{m}_{1}}+{{m}_{2}}}}\
i.e., {{X}_{{CM}}}=\frac{{{{m}_{2}}L}}{{{{m}_{1}}+{{m}_{2}}}};\ {{Y}_{{CM}}}=0\ \,\,\text{and}\ \,\,{{Z}_{{CM}}}=0\
i.e., centre of mass is at a distance [{{m}_{2}}L/({{m}_{1}}+{{m}_{2}})] from m1 internally on the line joining the two particles.
Illustration
The position vectors of three particles of mass m1 = 1 kg, m2 = 2 kg, and m3 = 3 kg are \overrightarrow{{{{r}_{1}}}}=(\hat{i}+4\hat{j}+\hat{k})\mathbf{m},\ \overrightarrow{{{{r}_{2}}}}=(\hat{i}+\hat{j}+\hat{k})\mathbf{m}\ \,\,\text{and}\,\,\ \overrightarrow{{{{r}_{3}}}}=(2\hat{i}-\hat{j}-2\hat{k})\mathbf{m} respectively. Find the position vector of their centre of mass.
Solution:
The position vector of CM of the three particles will be given by
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{{{{m}_{1}}\overrightarrow{{{{r}_{1}}}}+{{m}_{2}}\overrightarrow{{{{r}_{2}}}}+{{m}_{3}}\overrightarrow{{{{r}_{3}}}}}}{{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}}
Substituting the values, we get
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{{(1)\ (\hat{i}+4\hat{j}+\hat{k})+(2)(\hat{i}+\hat{j}+\hat{k})+3(2\hat{i}-\hat{j}-2\hat{k})}}{{1+2+3}} =\frac{{9\hat{i}+3\hat{j}-3\hat{k}}}{6}
{{\overrightarrow{{r\,}}}_{{CM}}}=\frac{1}{2}(3\hat{i}+\hat{j}-\hat{k})\text{m}Ans.
Centre of mass of a uniform Rod
Suppose a rod of mass M and length L is lying along the x-axis with its one end at x = 0 and the other at x = L.
Mass per unit length of the rod =\frac{M}{L}
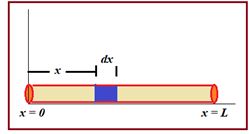
Hence, the mass of the element of length dx situated at x = x is dm=\frac{M}{L}dx
The coordinate of the element of length dx is (x, 0, 0). Therefore, x-coordinate of CM of the rod will be
{{x}_{{CM}}}=\frac{{\int\limits_{0}^{L}{{x\,dm}}}}{{\int{{dm}}}}
=\frac{{\int\limits_{0}^{L}{{(x)\,\left( {\frac{M}{L}dx} \right)}}}}{M}=\frac{1}{L}\int_{0}^{L}{{x\ dx}}=\frac{L}{2}
The y-coordinate of CM is
{{y}_{{CM}}}=\frac{{\int_{{}}^{{}}{{ydm}}}}{{\int_{{}}^{{}}{{dm}}}}=0
(as y = 0)
Similarly, zCM = 0
i.e., the coordinates of CM of the rod are \left( {\frac{L}{2},0,0} \right).
Proceeding in the similar manner, we can find the CM of certain rigid bodies. Centre of mass of some well known rigid bodies are given below:
1.
Centre of mass of a uniform rectangular, square or circular plate lies at their geometrical centre.
2.
Centre of mass of a uniform semicircular ring lies at a distance of h=\frac{{2R}}{\pi } from its centre, on the axis of symmetry where R is the radius of the ring.
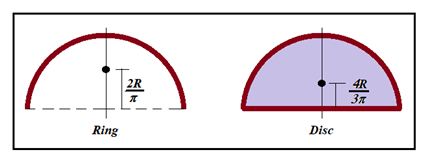
3.
Centre of mass of a uniform semicircular disc of radius R lies at a distance of h=\frac{{4R}}{{3\pi }} from the centre on the axis of symmetry.
4.
Centre of mass of a hemispherical shell of radius R lies at a distance of h=\frac{R}{2} from its centre on the axis of symmetry.
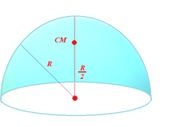
5.
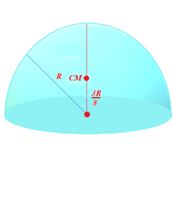
Centre of mass of a Solid hemisphere of radius R lies at a distance of h=\frac{{3R}}{8} from its centre on the axis of symmetry.
Illustration
Find the position of centre of mass of the uniform lamina shown in figure.
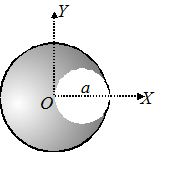
Solution
Here, A1 = area of complete circle =\pi {{a}^{2}}
A2 = area of small circle =\pi \,{{\left( {\frac{a}{2}} \right)}^{2}}=\frac{{\pi {{a}^{2}}}}{4}
(x1, y1) = coordinates of centre of mass of large circle = (0, 0)
and (x2, y2) = coordinates of centre of mass of small circle =\left( {\frac{a}{2},0} \right)
Using {{x}_{{\mathbf{CM}}}}=\frac{{{{A}_{1}}{{x}_{1}}-{{A}_{2}}{{x}_{2}}}}{{{{A}_{1}}-{{A}_{2}}}}
We get {{x}_{{\mathbf{CM}}}}=\frac{{-\frac{{\pi {{a}^{2}}}}{4}\left( {\frac{a}{2}} \right)}}{{\pi {{a}^{2}}-\frac{{\pi {{a}^{2}}}}{4}}}=\frac{{-\left( {\frac{1}{8}} \right)}}{{\left( {\frac{3}{4}} \right)}}a=-\frac{a}{6}
and {{y}_{{\mathbf{CM}}}}=0 as y1 and y2 both are zero.
Therefore, coordinates of CM of the lamina shown in figure are \left( {-\frac{a}{6},0} \right).
Motion of the centre of mass
The equations of motion of the centre of mass are as follows:
\overrightarrow{{{{V}_{{CM}}}\,}}=\frac{{\overrightarrow{{dR\,}}}}{{dt}}
M\frac{{\overrightarrow{{d{{V}_{{CM}}}\,}}}}{{dt}}=M\frac{{{{d}^{2}}\overrightarrow{{{{R}_{{CM}}}\,}}}}{{d{{t}^{2}}}}
or M\frac{{\overrightarrow{{d{{V}_{{CM}}}\,}}}}{{dt}}=\overrightarrow{{F\,}}
Working in terms of the centre of mass of the system gives us the advantage of ignoring the internal forces, internal motion and internal structure. We need to take into account only the external forces acting on the system.
Let us now establish a relation between the momentum of the system and the momentum of centre of mass of the system.
Let us consider a system consisting of n particles of masses m1, m2 …mn. The total mass M of the system is given by
M={{m}_{1}}+{{m}_{2}}+\ldots +{{m}_{n}}
The position vector of the centre of mass is given by
\overrightarrow{{{{R}_{{CM}}}\,}}=\frac{{{{m}_{1}}\overrightarrow{{{{r}_{1}}}}+{{m}_{2}}\overrightarrow{{{{r}_{2}}}}+\ldots +{{m}_{n}}\overrightarrow{{{{r}_{n}}}}}}{{{{m}_{1}}+{{m}_{2}}+\ldots +{{m}_{n}}}}
or \overrightarrow{{{{R}_{{CM}}}\,}}=\frac{{{{m}_{1}}\overrightarrow{{{{r}_{1}}}}+{{m}_{2}}\overrightarrow{{{{r}_{2}}}}+\ldots +{{m}_{n}}\overrightarrow{{{{r}_{n}}}}}}{M}
Differentiating both sides with respect to time t, we get
\frac{d}{{dt}}({{\overrightarrow{R}}_{{CM}}})=\frac{1}{M}\left[ {\frac{d}{{dt}}({{m}_{1}}\overrightarrow{{{{r}_{1}}}})+\frac{d}{{dt}}({{m}_{2}}\overrightarrow{{{{r}_{2}}}})+\ldots +\frac{d}{{dt}}({{m}_{n}}\overrightarrow{{{{r}_{n}}}})} \right]
or M\frac{{\overrightarrow{{d{{R}_{{CM}}}\,}}}}{{dt}}={{m}_{1}}\frac{{\overrightarrow{{d{{r}_{1}}}}}}{{dt}}+{{m}_{2}}\frac{{\overrightarrow{{d{{r}_{2}}}}}}{{dt}}+\ldots +{{m}_{n}}\frac{{\overrightarrow{{d{{r}_{n}}}}}}{{dt}}
But \frac{{\overrightarrow{{d{{R}_{{CM}}}\,}}}}{{dt}}=\overrightarrow{{{{V}_{{CM}}}\,}} (velocity of centre of mass)
\frac{{\overrightarrow{{d{{r}_{1}}}}}}{{dt}}=\overrightarrow{{{{v}_{1}}}},\frac{{\overrightarrow{{d{{r}_{2}}}}}}{{dt}}=\overrightarrow{{{{v}_{2}}}},\ldots ,\frac{{\overrightarrow{{d{{r}_{n}}}}}}{{dt}}=\overrightarrow{{{{v}_{n}}}}
Where \,\overrightarrow{{{{v}_{1}}}},\,\overrightarrow{{{{v}_{2}}}},\ldots \,\overrightarrow{{{{v}_{n}}}} are the velocities of the individual particles of the system.
M\,\overrightarrow{{{{V}_{{CM}}}\,}}={{m}_{1}}\overrightarrow{{{{v}_{1}}}}+{{m}_{2}}\overrightarrow{{{{v}_{2}}}}+\ldots +{{m}_{n}}\overrightarrow{{{{v}_{n}}}} …(i)
or M\,\overrightarrow{{{{V}_{{CM}}}\,}}=\sum\limits_{{i=1}}^{n}{{{{m}_{i}}\overrightarrow{{{{v}_{i}}}}}}
We conclude from this equation that the total momentum of the system is the same as the moment tum of the centre of mass
(ii)
Now let usestablish a relation between the force acting on the centre of mass and the forces acting on the individual particles of the system.
Differentiating both sides of equation (1) w.r.t. time, we get
\frac{d}{{dt}}(M\overrightarrow{{{{V}_{{CM}}}\,}})=\frac{d}{{dt}}({{m}_{1}}\overrightarrow{{{{v}_{1}}}})+\frac{d}{{dt}}({{m}_{2}}\overrightarrow{{{{v}_{2}}}})+\ldots +\frac{d}{{dt}}({{m}_{n}}\overrightarrow{{{{v}_{n}}}})
or M\frac{d}{{dt}}(\overrightarrow{{{{V}_{{CM}}}}})={{m}_{1}}\frac{d}{{dt}}(\overrightarrow{{{{v}_{1}}}})+{{m}_{2}}\frac{d}{{dt}}(\overrightarrow{{{{v}_{2}}}})+\ldots +{{m}_{n}}\frac{d}{{dt}}(\overrightarrow{{{{v}_{n}}}})
But \frac{d}{{dt}}(\overrightarrow{{{{V}_{{CM}}}}})=\overrightarrow{{{{A}_{{CM}}}\,}} (acceleration of centre of mass)
\frac{d}{{dt}}(\overrightarrow{{{{v}_{1}}}})=\overrightarrow{{{{a}_{1}}}},\frac{d}{{dt}}(\overrightarrow{{{{v}_{2}}}})=\overrightarrow{{{{a}_{2}}}},\ldots \frac{d}{{dt}}(\overrightarrow{{{{v}_{n}}}})=\overrightarrow{{{{a}_{n}}}}
Where \overrightarrow{{{{a}_{1}}}},\overrightarrow{{{{a}_{2}}}}\ldots \overrightarrow{{{{a}_{n}}}} are the acceleration of the individual particles of the system.
M\overrightarrow{{{{A}_{{CM}}}\,}}={{m}_{1}}\overrightarrow{{{{a}_{1}}}}+{{m}_{2}}\overrightarrow{{{{a}_{2}}}}+\ldots +{{m}_{n}}\overrightarrow{{{{a}_{n}}}}
Applying Newton’s 2nd law of motion,
\overrightarrow{{F\,}}=\overrightarrow{{{{F}_{1}}}}+\overrightarrow{{{{F}_{2}}}}+\ldots +\overrightarrow{{{{F}_{n}}}}
Here \overrightarrow{{F\,}} is the force acting on the centre of mass. This is clearly equal to the vector sum of the forces acting on the individual particles of the system.
Momentum conservation and motion of the centre of mass
The equation of motion of centre of mass is
\overrightarrow{{F\,}}=\frac{d}{{dt}}(M{{\vec{V}}_{{CM}}})
Where \overrightarrow{{F\,}} is the net external force acting on the system, M is the mass of the system and \displaystyle {{\vec{V}}_{{cm}}} is the velocity of the centre of mass of the system.
If no external force acts on the system, then \overrightarrow{{F\,}}=0.
\frac{d}{{dt}}(M{{\vec{V}}_{{CM}}})=0
\displaystyle M{{\vec{V}}_{{CM}}}=\text{constant} …(i)
{{m}_{1}}\overrightarrow{{{{v}_{1}}}}+{{m}_{2}}\overrightarrow{{{{v}_{2}}}}+\ldots +{{m}_{n}}\overrightarrow{{{{v}_{n}}}}=\text{constant} …(ii)
It is clear from equations (i) and (ii) that if no external force acts on the system, then the total momentum of the system is constant. This is law of conservation of momentum.
It is further clear from equation (i) that
{{\vec{V}}_{{CM}}}=\text{constant} (QM is constant)
Thus, if no external force acts on a system, then its centre of mass moves uniformly in a straight line. This is Newton’s first law of motion.
Illustration
In the arrangement shown in figure, {{m}_{A}}=2\mathbf{kg} and {{m}_{B}}=1\mathbf{kg} String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect friction everywhere.
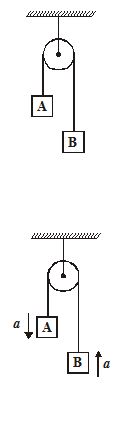
Solution:
Net pulling force on the system is ({{m}_{A}}-{{m}_{B}})g
or, (2-1)g=g
Total mass being pulled is ({{m}_{A}}+{{m}_{B}}) or 3 kg
a=\frac{{\text{Net}\ \text{pulling}\ \text{force}}}{{\text{Total}\ \text{mass}}}=\frac{g}{3}
Now, {{\overrightarrow{{a\,}}}_{{CM}}}=\frac{{{{m}_{A}}\overrightarrow{{{{a}_{A}}}}+{{m}_{B}}\overrightarrow{{{{a}_{B}}}}}}{{{{m}_{A}}+{{m}_{B}}}}
hence \left| {{{{\vec{a}}}_{{cm}}}} \right|=\frac{{(2)(a)-(1)(a)}}{{1+2}}=\frac{a}{3} =\frac{g}{9} downward.
Illustration
Two blocks A and B of equal masses are released on two sides of a fixed wedge C as shown in figure. Find the acceleration of centre of mass of blocks A and B. Neglect friction.
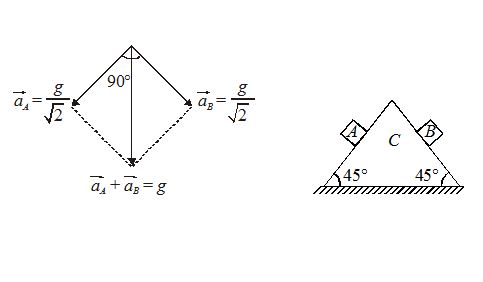
Solution:
Acceleration of both the blocks will be g\sin 45{}^\circ \,\text{or}\,\frac{g}{{\sqrt{2}}} at right angles to each other. Now,
{{\overrightarrow{{a\,}}}_{{CM}}}=\frac{{{{m}_{A}}\overrightarrow{{{{a}_{A}}}}+{{m}_{B}}\overrightarrow{{{{a}_{B}}}}}}{{{{m}_{A}}+{{m}_{B}}}}
Here, mA = mB
{{\overrightarrow{{a\,}}}_{{CM}}}=g downwards.
Illustration
Two particles of equal mass have velocity \overrightarrow{{{{v}_{1}}}}=2\hat{i}\,\text{m/s} and \overrightarrow{{{{v}_{2}}}}=2\hat{j}\,\text{m/s}\text{.} First particle has an acceleration \overrightarrow{{{{a}_{1}}}}=(3\hat{i}+3\hat{j})\,\text{m/}{{\text{s}}^{\text{2}}} while the acceleration of the other particle is zero. The centre of mass of the two particles moves on a
(1) circle
(2) parabola
(3) straight line
(4) ellipse
Solution:
{{\overrightarrow{{v\,}}}_{{COM}}}=\frac{{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}} =\frac{{\overrightarrow{{{{v}_{1}}}}+\overrightarrow{{{{v}_{2}}}}}}{2} Q ({{m}_{1}}={{m}_{2}})
=(\hat{i}+\hat{j})\,\text{m/s}
Similarly, {{\overrightarrow{{a\,}}}_{{COM}}}=\frac{{\overrightarrow{{{{a}_{1}}}}+\overrightarrow{{{{a}_{2}}}}}}{2}=\frac{3}{2}(\hat{i}+\hat{j})\,\text{m/}{{\text{s}}^{2}}
Since {{\overrightarrow{{v\,}}}_{{COM}}} is parallel to {{\overrightarrow{{a\,}}}_{{COM}}} the path will be a straight line
(3)
Illustration
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr, relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction of the pulley axis, the velocity of the centre of mass of this system is
(1) \frac{m}{M}{{v}_{r}}
(2) \frac{m}{{2M}}{{v}_{r}}
(3) \frac{M}{m}{{v}_{r}}
(4) \frac{{2M}}{m}{{v}_{r}}
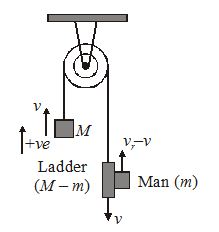
Solution:
The rope tension is the same on both the left and right hand side at every instant, and consequently momentum of both sides are equal
Mv=(M-m)\ (-v)+m({{v}_{r}}-v)
or v=\frac{m}{{2M}}{{v}_{r}}
Momentum of the centre of mass is P={{P}_{1}}+{{P}_{2}}
or {{v}_{{COM}}}=v=\frac{m}{{2M}}{{v}_{r}}
(2).
Illustration
Find the center of mass of a semicircular rod of radius R and linear density λ kg/m as shown in the figure.
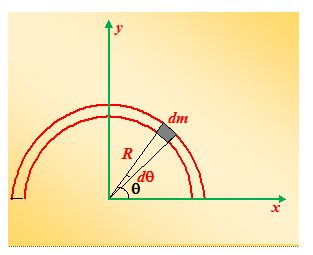
Solution
From the symmetry of the body we see that at once that the c.m. must lie along the y axis, so xc.m.= 0. In this case it is convenient to express the mass element in terms of the angle θ, measured in radians. The element, which subtends an angle dθ at the origin, has a length Rdθ and a mass dm = λRdq.
Here y = Rsinθ. Therefore, ycm= \int{{y\frac{{dm}}{M}}} takes the form
ycm= \displaystyle \frac{1}{M}\int\limits_{0}^{\pi }{{\lambda {{R}^{2}}\sin \theta \,d\theta }}=\frac{{\lambda {{R}^{2}}}}{M}\left[ {-\cos \theta } \right]_{0}^{\pi } = \frac{{2\lambda {{R}^{2}}}}{M}
The total mass of the ring is M = pRλ; therefore, ycm= 2R/π
Illustration
Find the center of mass of a uniform solid cone of height h and semiangle a, as shown in the figure
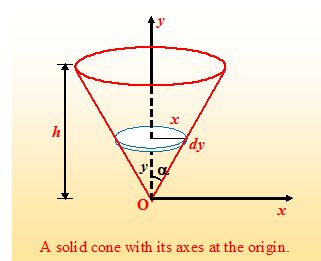
Solution
We assume the apex of the cone at the origin. It is clear that the c.m. will lie along the y axis. We divide the cone into disc of radius x and thickness dy. The volume of such a disc is
dV = πx2dy = π(y tanα)2 dy. The mass of the disc is dm = ρdV. Let us first find the total mass of the cone
M \int{{dm}}=\pi \rho {{\tan }^{2}}\alpha \int\limits_{0}^{h}{{{{y}^{2}}dy}}=\pi \rho {{\tan }^{2}}\alpha \frac{{{{h}^{3}}}}{3} (i)
The position of the c.m. is given by yc.m.= \frac{{\int{{y\,dm}}}}{M}
yc.m. = \frac{1}{M}\pi \rho {{\tan }^{2}}\alpha \int\limits_{0}^{h}{{{{y}^{3}}}}dy=\frac{1}{M}\pi \rho {{\tan }^{2}}\alpha \frac{{{{h}^{4}}}}{4} (ii)
Using (i) and (ii), we find
yc.m. = \frac{{3h}}{4}
Illustration
A man of mass m1= 60 kg is at the rear of a stationary boat of mass m2= 40 kg and length 3 m, which can move freely on the water, as shown in the figure. The front of the boat is 2 m from the dock. What happens when the man walks to the front? Treat the boat as a uniform object.
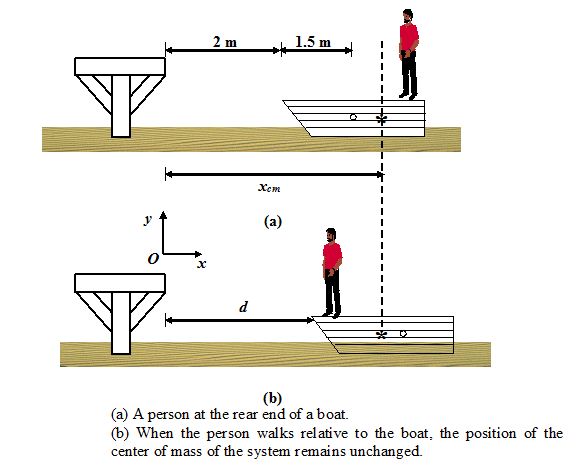
Solution
The initial position of the c.m. is indicated by a star as shown in the in figure. Since there is no net external force, xc.m.is fixed. We treat the boat as a point particle at its center. In terms of the initial positions,
xc.m.= \frac{{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}}{M}=\frac{{\left( {60\,\,kg} \right)\left( {5\,\,m} \right)+\left( {40\,\,kg} \right)\left( {3.5\,m} \right)}}{{100\,kg}}=4.4m (i)
After the man walks to the front, let us say the front is at a distance d from the dock as shown in figure. In terms of the new positions,
xc.m.= \frac{{{{m}_{1}}d+{{m}_{2}}\left( {d+1.5} \right)}}{{100}} (ii)
On equating (i) and (ii) we find d = 3.8 m.
The negative displacement of the man is accompanied by a positive displacement of the boat such that the cm stays fixed. The total momentum of the system remains zero at all times.
Practice Questions (Basic Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Practice Questions (JEE Main Level)
1.
Four particles each of mass m are placed at the four corners of a square of side a as shown. The (x, y) coordinates of centre of mass are
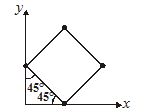
(a) \left( {\frac{a}{{\sqrt{2}}},\frac{a}{{\sqrt{2}}}} \right)
(b) \left( {a\sqrt{2},a\sqrt{2}} \right)
(c) \left( {\frac{a}{2},\frac{a}{2}} \right)
(d) (a, a)
Ans (a)
2.
A thin uniform disc of shape half of the ellipse with major axis 2a and minor axis 2b, is shown. Find x coordinate of centre of mass
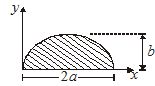
(a) a
(b) \frac{{3a}}{2}
(c) \frac{{3b}}{4}
(d) \frac{b}{4}
Ans (a)
3.
A meter stick is placed vertically at the origin on a frictionless surface. A gentle push in + x direction is given to the top most point of the rod. What will be the position of the lowest point of the rod, when it has fallen completely?
(a) origin
(b) –0.5 m
(c) –1 m
(d) + 0.5 m
Ans (b)
4.
A cyclist moves in a circular track of diameter d and with speed v. He leans at an angle of q from the vertical. Then q is equal to
(a) {{\tan }^{{-1}}}\left( {\frac{{{{v}^{2}}}}{{dg}}} \right)
(b) {{\tan }^{{-1}}}\left( {\frac{{2{{v}^{2}}}}{{dg}}} \right)
(c) {{\tan }^{{-1}}}\left( {\frac{{{{v}^{2}}}}{{8dg}}} \right)
(d) {{\tan }^{{-1}}}\left( {\frac{{{{v}^{2}}}}{g}} \right)
Ans (b)
5.
Two heavenly bodies of mass m and 2m moves towards each other under mutual force of attraction. Then acceleration of centre of mass of the system having both bodies is
(a) greater than acceleration of heavier body but smaller than acceleration of lighter body
(b) greater that acceleration of lighter body but smaller than acceleration of lighter body
(c) greater than acceleration of both the bodies
(d) always zero
Ans (d)
6.
All the particles of a body are situated at a distance R from the origin. The distance of centre of mass of the body from the origin is:
(a) = R
(b) < R
(c) >R
(d) > R
Ans (b)
7.
Two blocks of mass 10 kg and 30 kg are placed along a vertical line. The first block is raised through a height of 7 cm. By what distance should the second mass be moved to raised the centre of mass by 1cm?
(a) 2 cm upward
(b) 1 cm upward
(c) 2 cm downward
(d) 1 cm downward
Ans (d)
8.
Two persons A and B having masses 50 kg and 60 kg respectively are sitting at the two extreme to a 4 m long platform of mass 40 kg kept on smooth ice. If they come to the middle of the boat then how (approximately) far does the boat move on the ice during the process?
(a) 10 cm
(b) 11 cm
(c) 12 cm
(d) 13 cm
Ans (d)
9.
Two vehicles of equal masses are moving with same speed v on two roads inclined at an angle q. They collide inelastically at the junction and then move together. The speed of the combination is:
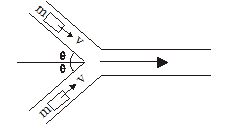
(a) v cos q
(b) 2v cos q
(c) \frac{v}{2}\cos \,\theta
(d) \frac{v}{2}\cos \,\frac{\theta }{2}
Ans (a)
10.
Two particles P and Q initially at rest, move towards each other under a mutual force of attraction. At the instant when the speed of P is v and the speed of Q is 2v, the speed of the centre of mass of the system is:
(a) 3v
(b) 1.5v
(c) v
(d) zero
Ans (d)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
