Video Lecture
Theory For Making Notes
Calorimetry, Concept Of Latent Heat And Specific Heat
Study of heat exchange is known as calorimetry. It is use to determine specific heat and latent heat of substance.
Specific heat capacity and molar heat capacity
When heat is supplied to a body the temperature of the body increases. The increase in temperature of the body depends upon the mass of the substance, heat supplied, the material of the body as well as the surrounding conditions. We write the equation.
Q=mc\Delta t … (i)
Where Δt is the change in temperature m is the mass of the body, Q is the heat supplied and s is a constant for given material under the given surrounding conditions. The constant s is called specific heat capacity of the substance.
The SI unit for specific heat capacity is J/kg–K or J/kg–°C. The specific heat capacity is also called specific heat in short. The amount of substance in the given body may also be measured in terms of number of moles. So equation (1) may be rewritten as
Q = nCΔt … (ii)
Where n is the number of moles in the sample. The constant C is called molar heat capacity.
Mathematically specific heat is defined as heat exchange to change the temperature by unity of unit mass body.
C=\frac{{\Delta Q}}{{m\Delta \,t}} If m=1,\,\,\Delta t=1,\,\,\,C=\Delta Q
Specific heat depends on (i) type and nature of material (ii) temperature (iii) state of matter.
{{C}_{{gas}}}>{{C}_{{liquid}}}>{{C}_{{solid}}}
DEFINITION OF ONE CALORIE
Amount of heat required to raise the temperature of one gm water from 14.5°C to 15.5°C under one atmospheric pressure.
Mechanical equivalent of heat
Since we define heat as energy in transit hence it can be compared to work. In fact we do have a relation, which tells us that how much mechanical energy is equivalent to work. If mechanical work W joule produces the same temperature difference as is produced by a heat H calories then we write.
W = JH
Where J is called mechanical equivalent of heat. The unit of J is joule/calorie.
J=4.2\,\,J/cal
Heat Capacity
The heat capacity C of an object is the proportionality constant between the heat Q that the object absorbs or loses and the resulting temperature change ΔT of the object; that is,
Q=C\Delta T=C({{T}_{f}}-{{T}_{i}}),
in which Ti and Tf are the initial and final temperatures of the object. Heat capacity C has the unit of energy per degree or energy per Kelvin.
LATENT HEAT
The amount of energy per unit mass that must be transferred as heat when a sample completely undergoes a phase change is called the heat of transformation L. This is also known as latent heat. Thus, when a sample of mass m completely undergoes a phase change, the total energy transferred is
Q=Lm
When the phase change is from liquid to gas (then the sample must absorb heat) or from gas to liquid (then the sample must release heat), the heat of transformation is called the heat of vaporization LV. For water at its normal boiling or condensation temperature,
LV = 539 cal/g = 40.7 kJ/mol = 2256 kJ/kg.
When the phase change is from solid to liquid (then the sample must absorb heat) or from liquid to solid (then the sample must release heat), the heat of transformation is called the heat of fusion LF. For water at its normal freezing or melting temperature,
Lf = 79.5 cal/g = 6.01 kJ/mol = 333 kJ/kg.
Water equivalent
Water equivalent of the body is the mass of water, which when given same amount of heat as given to the body changes the temperature of water through same range as that of the body.
w=m\,c
w= water equivalent
m=mass of body
c=specific heat of body
It’s unit is kg.
LAW OF Calorimetry
When two bodies at different temperatures are mixed heat will be transfer from higher temperature to at lower temperature till both body acquire temperature.
Heat lost by hotter body = Heat gained by colder body.
Temperature of mixture cannot be greater than hotter body and lesser than colder body.
Mixing of two substances when temperature changes only : It means no phase change. Suppose two substances having masses {{m}_{1}} and {{m}_{2}} , gram specific heat {{c}_{1}} and {{c}_{2}} , temperatures {{t}_{1}} and {{t}_{2}} ({{t}_{1}}>{{t}_{2}})are mixed together such that temperature of mixture at equilibrium is tmix
Hence, Heat lost = Heat gained
Þ {{m}_{1}}{{c}_{1}}({{t}_{1}}-{{t}_{{mix}}})={{m}_{2}}{{c}_{2}}({{t}_{{mix}}}-{{t}_{2}})
hence {{t}_{{mix}}}=\frac{{{{m}_{1}}{{c}_{1}}{{t}_{1}}+{{m}_{2}}{{c}_{2}}{{t}_{2}}}}{{{{m}_{1}}{{c}_{1}}+{{m}_{2}}{{c}_{2}}}}
Specific heat for Solids
When a solid is heated through a small range of temperature, its volume remains more or less constant. Therefore specific heat of a solid may be called its specific heat at constant volume CV.
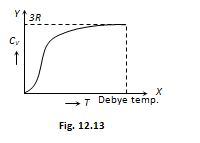
From the graph it is clear that at T = 0, CV tends to zero whereas with rise in temperature, CV increases and at a particular temperature (called Debey’s temperature) it becomes constant = 3R = 6 cal/molekelvin = 25 J/molekelvin
(4) Dulong and Petit law : Average molar specific heat of all metals at room temperature is constant, being nearly equal to 3R = 6 cal. mole–1K–1 = 25 Jmole–1K–1, where R is gas constant for one mole of the gas. This statement is known as Dulong and Petit law.
(5) Debey’slaw :It was observed that at very low temperature molar specific heat µ {{T}^{3}} (exception are Sn, Pb and Pt)
Heating Curve
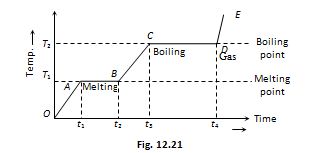
If to a given mass (m) of a solid, heat is supplied at constant rate P (where P=Q/Δt) and a graph is plotted between temperature and time, the graph is as shown in figure and is called heating curve. From this curve it is clear that
1.
In the region OA temperature of solid is changing with time so, Q=m{{c}_{S}}\Delta T
P\,\Delta t=m{{c}_{S}}\Delta T [asQ = PΔt]
But as (ΔT/Δt) is the slope of temperature-time curve
{{c}_{s}}\propto \frac{1}{{\text{Slope of line }OA}}
i.e. specific heat (or thermal capacity) is inversely proportional to the slope of temperature-time curve.
(2)
In the region AB temperature is constant, so it represents change of state, i.e., melting of solid with melting point T1. At A melting starts and at B all solid is converted into liquid. So between A and B substance is partly solid and partly liquid. If LF is the latent heat of fusion. Q=m{{L}_{F}} or {{L}_{F}}=\frac{{P({{t}_{2}}-{{t}_{1}})}}{m} [as Q=P({{t}_{2}}-{{t}_{1}})]
or LFµ length of line AB
i.e. Latent heat of fusion is proportional to the length of line of zero slope. [In this region specific heat µ \frac{1}{{\tan 0}}=\infty ]
(3)
In the region BC temperature of liquid increases so specific heat (or thermal capacity) of liquid will be inversely proportional to the slope of line BC
i.e., {{c}_{L}}\propto \frac{1}{{\text{Slope of line }B\text{C}}}
(4)
In the region CD temperature is constant, so it represents the change of state, i.e., boiling with boiling point T2. At C all substance is in liquid state while at D in vapour state and between C and D partly liquid and partly gas. The length of line CD is proportional to latent heat of vaporisation
i.e., LVµ Length of line CD [In this region specific heat µ \frac{1}{{\tan 0}}=\infty ]
(5)
The line DE represents gaseous state of substance with its temperature increasing linearly with time. The reciprocal of slope of line will be proportional to specific heat or thermal capacity of substance in vapour state.
Illustration
How should one kg of water at 5°C be so divided that one part of it when converted into ice at 0°C, would by this change of state provide a quantity of heat that would be sufficient to vaporize the other part?
Solution:
Initially 1000 g of water is at 5°C.
Let m gram of it be cooled to ice at 0°C.
Heat released due to this = (m x 1 x 5) + (m x 80) = 5m + 80m = 85m cal.
The heat required by (1000 – m) g of water at 5°C to become steam at 100°C
= (1000 – m) (100 – 5) + (1000 – m) 540 cal
= (1000 – m) (95 + 540) cal
= (1000 – m) (635) cal
Now, 85 m = (1000 – m) 635 or 720 m = 635 ´ 1000
m = \frac{{635\times 1000}}{{720}} = 881.9 g
Hence 881.9 g of water by turning into ice at 0°C will supply heat to evaporate 118.1 g of water.
Illustration
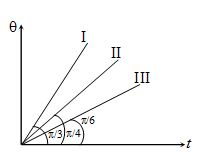
Three bodies A, B and C of masses m, m and \sqrt{{3\,\,}}m respectively are supplied heat at a constant rate. The change in temperature q versus time t graph for A, B and C are shown by I, II and III respectively. If their specific heat capacities are SA, SB and SC respectively then which of the following relation is correct? (Initial temperature of each body is 0°C)
(a) SA>SB>SC
(b) SB = SC<SA
(c) SA = SB = SC
(d) SB = SC>SA
Solution
If R is rate of heating, \Delta Q=ms(\theta )
Rt=ms\theta \theta =\left( {\frac{R}{{ms}}} \right)t
Slope of q-t curve =\frac{R}{{ms}}=\tan \varphi {{S}_{B}}={{S}_{C}}>{{S}_{A}}
(d)
Illustration
100 g of ice at 0°C is mixed with 100 g of water at 100°C. What will be the final temperature of the mixture?
(a) 10°C
(b) 20°C
(c) 30°C
(d) 0°C
Solution
Let the final temperature of mixture be q.
Then 100 x 80 + 100(q – 0) = 100 x 1 x (100 – q)
Solving, we get q = 10°C
(a)
Illustration
1 kg water of specific heat 1 cal/gm-0C is kept in a container at 100 C. If 50 gm of ice at 00C is required to cool down the water from 100C to 00C, the water equivalent of container is
(Latent of fusion for ice = 80 cal/gm and specific heat of water is 1 cal/gm-0C0)
(a) 1 kg
(b)2 kg
(c) 3 kg
(d) \frac{1}{2}kg
Solution
\left( {m+1000} \right)\times 1\times 10=50\times 80
\left( {m+1000} \right)=4000
m=3000gm = 3 kg
(c)
Illustration
Two litres of water at initial temperature of 27°C is heated by a heater of power 1 kW in a kettle. If the lid of the kettle is open, then heat energy is lost at a constant rate of 160 J/s. The time in which the temperature will rise from 27°C to 77°C is (specific heat of water
= 4.2 kJ/kg)
(a) 5 min. 20 sec.
(b) 8 min. 20 sec.
(c) 10 min. 40 sec.
(d) 12 min. 50 sec.
Solution
Heat gained by water = Heat supplied – Heat loss
ms\Delta \theta =1000t-160t t=\frac{{2\times 4200\times 50}}{{840}}=8\min .20\sec .
(b)
Practice Questions (Basic Level)
1.
Heat required to convert 1g of ice at 0°C into steam at 100°C is (Latent heat of steam =536\,\,cal\,{{g}^{{-1}}})
(a) 100 cal
(b) 0.01 kcal
(c) 716 cal
(d) 1 kcal
Ans (c)
2.
200 gram of water at 48°C is mixed with 100 gram of water at 30°C. The resulting temperature of water is
(a) 39°C
(b) 42°C
(c) 36°C
(d) 45°C
Ans(b)
3.
The temperatures of equal masses of three different liquids A, B and C are 12°C, 19°C and 28°C respectively. The temperatures when A and B are mixed is 16°C and when B and C are mixed is 23°C. If A and C are mixed, the temperature will be
(a) 20.3°C
(b) 19.8°C
(c) 18.2°C
(d) 21.6°C
Ans (a)
4.
10 g of ice at –20°C is added to 10 g of water at 50°C. Then the resulting temperature is (Specific heat of ice =0.5\,cal\,{{g}^{{-1}}}\,{}^\circ {{C}^{{-1}}} and latent heat of ice =80\,cal\,{{g}^{{-1}}})
(a) –20°C
(b) 15°C
(c) 0°C
(d) 25°C
Ans (c)
5.
Hailstone at 0°C falls from a height of 1 km on an insulating surface converting whole of its kinetic energy into heat. What part of it will melt? (Given )
(a) \frac{1}{{33}}
(b) \frac{1}{8}
(c) \frac{1}{{33}}\times {{10}^{{-4}}}
(d) All of it will melt
Ans (a)
6.
An electric kettle contains 1.5 kg of water at 100°C and is powered by a 2.0 kW electric element. If the thermostat of the kettle fails to operate, approximately how long will the kettle take to boil dry? (Take the specific latent heat of vaporization of water as 2000 kJ k{{g}^{{-1}}})
(a) 500 s
(b) 1000 s
(c) 1500 s
(d) 3000 s
Ans (c)
Practice Questions (JEE Main Level)
1.
Three liquids with masses are thoroughly mixed. If their specific heats are {{s}_{1}},{{s}_{2}},{{s}_{3}} and their temperatures {{\theta }_{1}},{{\theta }_{2}},{{\theta }_{3}} respectively, then the temperature of the mixture is
(a) \frac{{{{s}_{1}}{{\theta }_{1}}+{{s}_{2}}{{\theta }_{2}}+{{s}_{3}}{{\theta }_{3}}}}{{{{m}_{1}}{{s}_{1}}+{{m}_{2}}{{s}_{2}}+{{m}_{3}}{{s}_{3}}}}
(b) \frac{{{{m}_{1}}{{s}_{1}}{{\theta }_{1}}+{{m}_{2}}{{s}_{2}}{{\theta }_{2}}+{{m}_{3}}{{s}_{3}}{{\theta }_{3}}}}{{{{m}_{1}}{{s}_{1}}+{{m}_{2}}{{s}_{2}}+{{m}_{3}}{{s}_{3}}}}
(c) \frac{{{{m}_{1}}{{s}_{1}}{{\theta }_{1}}+{{m}_{2}}{{s}_{2}}{{\theta }_{2}}+{{m}_{3}}{{s}_{3}}{{\theta }_{3}}}}{{{{m}_{1}}{{\theta }_{1}}+{{m}_{2}}{{\theta }_{2}}+{{m}_{3}}{{\theta }_{3}}}}
(d) \frac{{{{m}_{1}}{{\theta }_{1}}+{{m}_{2}}{{\theta }_{2}}+{{m}_{3}}{{\theta }_{3}}}}{{{{s}_{1}}{{\theta }_{1}}+{{s}_{2}}{{\theta }_{2}}+{{s}_{3}}{{\theta }_{3}}}}
Ans (b)
2.
During melting process, the heat given to a body is utilized in
(a) increasing the temperature
(b) increasing the density of material
(c) increasing the average distance of the molecules
(d) decreasing the average distance of the molecules
Ans (c)
3.
A calorimeter contains 0.2 kg of water at 30°C. 0.1 kg of water at 60°C is added to it, the mixture is well stirred and the resulting temperature is found to be 35°C. The thermal capacity of the calorimeter is
(a) 6300 J/K
(b) 1260 J/K
(c) 4200 J/K
(d) none of these
Ans (b)
4.
If specific heat of a substance is infinite. It means
(a) heat is given out
(b) heat is taken in
(c) no change in temperature takes place whether heat is taken in or given out
(d) all of the above
Ans (c)
5.
It takes 10 min for an electric kettle to heat a certain quantity of water from 0°C to 100°C. If it takes 54 min to convert this water at 100°C into steam, then latent heat of steam is
(a) 80 cal/gm
(b) 540 cal/kg
(c) 540 cal/gm
(d) 80 cal/kg
Ans (c)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
