Video Lectures
Theory For Notes Making
INTRODUCTION
A projectile motion near the surface of the earth consists of two independent motions, a horizontal motion at constant speed and a vertical one subject to the acceleration due to gravity.
In order to deal with problems in projectile motion, one has to choose a coordinate system and clearly specify the origin. If the x axis is horizontal and the y-axis points vertically
ax= 0 and ay = –g
One can easily assume the origin such that the initial horizontal coordinate is zero.
i.e. xo= 0
The equations of kinematics for projectile motion are
x = uxt
vy= uy–gt
y = yo+ uyt – \displaystyle \frac{1}{2}gt2 \displaystyle v_{y}^{2}\,=\,u_{y}^{2}-2g (y–yo)
A bomb is fired from a cannon with a velocity of 1000 m/s making an angle of 30o with the horizontal (g = 10 m/s2).
(i) What is the time taken by the bomb to reach the highest point?
(ii) What is the total time of its motion ?
(iii) With what speed the bomb will hit the ground and what will be its direction of motion while hitting?
(iv) What is the maximum height attained by the bomb?
(v) At what distance from the cannon the bomb will hit the ground ?
Solution
(i) Let u be the initial velocity of the bomb and qo its angle of projection. The time taken by the bomb to reach the highest point is given by
t = \displaystyle \frac{{u\sin {{\theta }_{o}}}}{g}=\frac{{1000\times \sin 30{}^\circ }}{{10}}=\frac{{1000\times \frac{1}{2}}}{{10}} = 51 s
(ii) The total time of its motion is, T = 2t = 2 x 51 = 102 s.
(iii) The bomb will hit the ground with the same speed with which it was fired. Hence its speed of hitting = 1000 m/s. Also, the angle of hitting with respect to the horizontal is 30o.
(iv) The maximum height attained by the bomb is
h = \displaystyle \frac{{{{u}^{2}}{{{\sin }}^{2}}{{\theta }_{o}}}}{{2g}}
= \displaystyle \frac{{{{{\left( {1000} \right)}}^{2}}\times {{{\sin }}^{2}}{{{30}}^{o}}}}{{2\times 10}}=\frac{{{{{\left( {1000} \right)}}^{2}}\times {{{\left( {0.5} \right)}}^{2}}}}{{2\times 10}} =1.25 x 104 m
(v) Horizontal range is
R = \displaystyle \frac{{{{u}^{2}}\sin 2{{\theta }_{o}}}}{g}=\frac{{{{{\left( {1000} \right)}}^{2}}\times \sin {{{60}}^{o}}}}{{10}} = 8.66 x 104 m
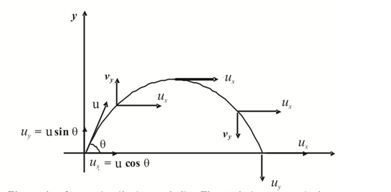
The Path Of a Projectile Is Parabolic.The Path Is Symmetrical About The Highest Point Only If The Particle Lands On the Same Level From Which It Was Fired.
Let us consider the case when a ball is projected from the ground with an initial velocity u at an angle θ above the horizontal
The origin is assumed at the point of projection. The instantaneous x and y coordinates of the ball are given by
x = (u cos θ) t …(1)
y = (u sin θ) t-1/2gt2 …(2)
To find the time of flight
That is time from point of projection to a point on the same horizontal level passing through the point of projection
we put y = 0 in equation (2)
0 = (u sin θ) t-1/2gt2
or t = \displaystyle \frac{{2u\sin \theta }}{g} …(3)
Note :
Time of flight is maximum at = 90º
To find the horizontal range
we substitute (3) in (1)
R = (ucos θ) \displaystyle \left( {\frac{{2u\sin \theta }}{g}} \right)
or R = \displaystyle \frac{{u_{{}}^{2}\,\sin 2\theta }}{g}
Note :
(i) Horizontal range is maximum at an angle of projection of 45º.
(ii) Range is same at two complimentary angle and θ and 90 – θ
(iii) maximum range at is equal to \displaystyle \frac{{u_{{}}^{2}}}{g}
The maximum height H for the projectile
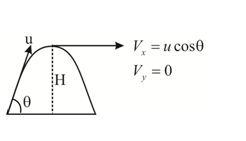
\displaystyle v_{y}^{2}\,=\,u_{y}^{2}\,-2gH
Since vy=0, therefore,
H = \displaystyle \frac{{u_{y}^{2}}}{{2g}}\,=\frac{{u_{{}}^{2}\,{{{\sin }}^{2}}\theta }}{{2g}} …(4)
The trajectory of the projectile
We have to express y in terms of x. Therefore eliminating t from (1) and (2), we get
y = x tan θ- \displaystyle \frac{g}{{2{{{\left( {u\cos \theta } \right)}}^{2}}}}\,{{x}^{2}} … (5)
Illustration
A ball is projected horizontally at 20 m/s from a cliff of height 45 m
(a) Find its time of flight
(b) Find its horizontal range R (the horizontal displacement from the point of firing).
Solution
The origin is assumed to be at the base of the cliff
Given: xo=0; yo= 45 m; vox= 20 m/s and voy= 0
The coordinates at a latter time are given by
x = 20 t … (i)
x = 45 – 5t2 … (ii)
(a) When the ball lands, its vertical coordinate is zero
i.e. y = 0 From (ii) , we get
y = 45 – 5t2 or t = 3 s
(b) To find the horizontal range we use the horizontal velocity and the time of flight.
R = voxt = (20) (3) = 60 m
Illustration
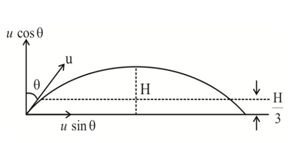
Find the average velocity of a projectile between the instants it crosses one third the maximum height. It is projected with u making an angle q with the vertical.
(a) u cos q
(b) u
(c) u sin q
(d) u tan q
Solution
Note carefully the vertical velocities at the same height are in opposite direction and therefore their average sum = 0. It is horizontal velocity which is uniform and hence vav = u sin θ( = ux)
Illustration
A person observes a bird on a tree 40 m high and at a distance of 60 m. With what velocity the person should throw an arrow at an angle of 45o so that it may hit the bird? g = 10 m/s2.
Solution
Let u be the initial velocity of the arrow and let it hit the bird after t.
The horizontal component of velocity u is u cos 45o = \frac{u}{{\sqrt{2}}}. Hence the horizontal distance traveled in t s is \frac{u}{{\sqrt{2}}}x t = 60 … (1)
The vertical distance traveled in time t s is 40 m, acceleration g = – 10 m/s2 and initial vertical velocity = u sin 45o = \frac{u}{{\sqrt{2}}}. Hence by the formula h = ut + \displaystyle \frac{1}{2}gt2, we have
40 = \displaystyle \frac{u}{{\sqrt{2}}}t-\frac{1}{2}\left( {10} \right){{t}^{2}} … (2)
By equation (1) and (2), we get
40 = 60 – \displaystyle \frac{1}{2}\left( {10} \right){{t}^{2}}
or t2 = \displaystyle \frac{{60-40}}{5}=\frac{{20}}{5}=4
t = 2 s
Substituting the value of t in equation (1), we get
\frac{u}{{\sqrt{2}}}´ 2 = 60
u = 30 \displaystyle \sqrt{2} m/s
Illustration
A bomb is fired from a cannon with a velocity of 1000 m/s making an angle of 30o with the horizontal (g = 10 m/s2).
(i) What is the time taken by the bomb to reach the highest point?
(ii) What is the total time of its motion ?
(iii) With what speed the bomb will hit the ground and what will be its direction of motion while hitting?
(iv) What is the maximum height attained by the bomb?
(v) At what distance from the cannon the bomb will hit the ground ?
Solution
(i) Let u be the initial velocity of the bomb and qo its angle of projection. The time taken by the bomb to reach the highest point is given by
t = \displaystyle \frac{{u\sin {{\theta }_{o}}}}{g}=\frac{{1000\times \sin 30{}^\circ }}{{10}}=\frac{{1000\times \frac{1}{2}}}{{10}} = 51 s
(ii) The total time of its motion is, T = 2t = 2 x 51 = 102 s.
(iii) The bomb will hit the ground with the same speed with which it was fired. Hence its speed of hitting = 1000 m/s. Also, the angle of hitting with respect to the horizontal is 30o.
(iv) The maximum height attained by the bomb is
h = \displaystyle \frac{{{{u}^{2}}{{{\sin }}^{2}}{{\theta }_{o}}}}{{2g}}
= \displaystyle \frac{{{{{\left( {1000} \right)}}^{2}}\times {{{\sin }}^{2}}{{{30}}^{o}}}}{{2\times 10}}=\frac{{{{{\left( {1000} \right)}}^{2}}\times {{{\left( {0.5} \right)}}^{2}}}}{{2\times 10}} =1.25 x 104 m
(v) Horizontal range is
R = \displaystyle \frac{{{{u}^{2}}\sin 2{{\theta }_{o}}}}{g}=\frac{{{{{\left( {1000} \right)}}^{2}}\times \sin {{{60}}^{o}}}}{{10}} = 8.66 x 104 m
Illustration
A ball is thrown from the top of a tower with an initial velocity of 10 m/s at an angle of 30o with the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. Calculate the height of the tower. (g = 10 m/s2)
Solution
The angle of projection of the ball is qo (=30o) and the velocity of projection is u (= 10 m/s). Resolving u in horizontal and vertical components, we have horizontal component,
ux= u cos qo = 10 cos 30o = 8.65 m/s
and vertical component (upward), uy= u sin30o = 5 m/s.
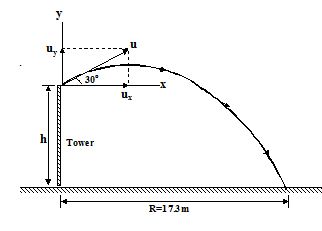
f the ball hits the ground after time t of projection, then the horizontal range is
R = ux X t = 8.65 t m
t = \displaystyle \frac{R}{{8.65}}=\frac{{17.3}}{{8.65}} = 2 s
If h be the height of the tower, then
h = uyt + \frac{1}{2}gt2
Here uy= 5 m/s , t = 2 s and g = -10m/s2
h = (5) x 2 + 1/2 x (-10) x (2)2 = 10 – 20 = – 10 m
The negative sign shows that the displacement is negative (downward).
Thus the height of the tower = 10 m
Illustration
A foot ball is kicked with a velocity of 20 m/s at an angle of 45° with the horizontal. (a) Find the time taken by the ball to strike the ground, (b) Find the maximum height it reaches. (c) How far away from the kick does it hit the ground? Take g = 10 m/s2.
Solution
(a) Take the origin at the point where the ball is kicked, vertically upward as the Y-axis and the horizontal in the plane of motion as the X-axis. The initial velocity has the components
\displaystyle {{u}_{x}}=(20\text{m/s})\cos 45{}^\circ =10\sqrt{2}\text{m/s}
& \displaystyle {{u}_{y}}=(20\text{m/s})\sin 45{}^\circ =10\sqrt{2}\text{m/s}
When the ball reaches the ground, y = 0.
Using \displaystyle y={{u}_{y}}t-\frac{1}{2}g{{t}^{2}}
\displaystyle 0=(10\sqrt{2}\text{m/s})t-\frac{1}{2}\times (10\,\text{m/}{{\text{s}}^{2}})\times {{t}^{2}}
or, \displaystyle t=2\sqrt{2}s=2.8s.
Thus, it takes 2.8s for the football to fall on the ground
(b) At the highest point Using the equation
\displaystyle v_{y}^{2}=u_{y}^{2}-2gy,
\displaystyle 0={{(10\sqrt{2}\text{m/s})}^{2}}-2\times (10\text{m/}{{\text{s}}^{2}})H
or, H = 10m.
Thus, the maximum height reached is 10 m.
(c) The horizontal distance traveled before falling to the ground is
x = uxt
x = \displaystyle (10\sqrt{2}\text{m/s})\,\,(2\sqrt{2}\text{s})=40\text{m}
Illustration
A ball is projected with velocity v0 and at an angle of projection a. After what time is the ball moving at right angles to the initial direction?
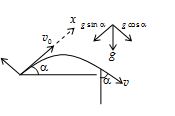
Solution
We choose x-axis along the initial velocity. If after time t the velocity is perpendicular to initial direction, vx must be zero after time t,
i.e. \displaystyle 0={{v}_{0}}-(g\sin \alpha )t
or \displaystyle t=\frac{{{{v}_{0}}}}{{g\sin \alpha }}
Objective Assignment
1.
Which of the following is the largest when the height attained by projectile is the greatest?
(a) Angle of projectile with the vertical (b) Range
(c) Time of light (d) None of these
Ans (b)
2.
A projectile is thrown to have the maximum possible horizontal range of 400 m. Taking the point of projection as the origin, the co-ordinate of the point where the velocity of the projectile is minimum are
(a) (400m, 200m) (b) (200m, 200m)
(c) (400m, 100m) (d) (200m, 100m)
Ans (d)
3.
In case of a projectile, what is the angle between its instantaneous velocity and acceleration at the highest point?
(a) 180° (b) 90° (c) 45° (d) 0°
Ans (b)
4.
The range of a projectile when fired at 75° with the horizontal is 0.5 km. What will be its range when fired at 45°?
(a) 2 km (b) 1.5 km (c) 1 km (d) 0.5 km
Ans (c)
5.
If a man wants to hit a target, he should aim his rifle in a direction:
(a) Lower than the target (b) Of the target
(c) Higher than the target (d) None of these
Ans (c)
6.
The x and y coordinates of a particle at any time t are given by x=7t+4{{t}^{2}} and y=5t where x and y are in metre and t in second. The acceleration of the particle at t=5s is
(a) \mathbf{40}\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}} (b) 20\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}} (c) \mathbf{8}\,\,\mathbf{m}{{\mathbf{s}}^{{-\mathbf{2}}}} (d) Zero
Ans (c)
7.
The coordinate of a moving particle at any instant of time t are x= at and y=b{{t}^{2}}. The trajectory of the particle is
(a) y=\frac{{{{b}^{2}}x}}{{{{a}^{2}}}} (b) y=\frac{{{{b}^{2}}{{x}^{2}}}}{{{{a}^{2}}}} (c) {{y}^{2}}=\frac{{{{b}^{2}}x}}{{{{a}^{2}}}} (d) y=\frac{{b{{x}^{2}}}}{{{{a}^{2}}}}
Ans (d)
8.
The equation of motion of a projectile is y=12x-\frac{3}{4}{{x}^{2}}. What is the range of the projectile?
(a) 3m (b) 4m (c) 12m (d) 16m
Ans (c)
9.
A passenger traveling in a train, which is moving with constant velocity, drops a stone from the window. To the passenger, the path of projectile will appear to be:
(a) An arc of a circle (b) An elliptical (c) A straight line (d) A parabola.
Ans (c)
10.
Two projectiles are fired at different angles with the same magnitude of velocity such that they have the same range. At what angles they might have been projected?
(a) 35° and 75° (b) 25° and 65° (c) 10° and 50° (d) None of these
Ans (b)
11.
Four projectiles are fired with the same speed at the angles 25°, 40°, 55° and 70° with the horizontal. The range of projectile will be largest for the one projected at an angle
(a) 70° (b) 40° (c) 55° (d) 25°
Ans (b)
12.
From the top of a tower, which is 19.6 m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45° with the horizontal, then the initial velocity of the ball is
(a) 9.8 m/s (b) 4.9 m/s (c) 14.7 m/s (d) 2.8 m/s
Ans (a)
13.
The pervious question, the magnitude of the velocity of ball when it collide with the ground is
(a)9.8m/s (b) 9.8\sqrt{3}\,\mathbf{m/s} (c) 19.6 m/s (d) 9.8\sqrt{5}\,\mathbf{m/s}
Ans (d)
14.
An aero-plane is moving horizontally with a velocity of magnitude u. It drops a packet when it is at a height h. The time taken by the packet to reach the ground is
(a) \sqrt{{\frac{{2u}}{g}}} (b) \sqrt{{\frac{{2g}}{h}}} (c) \sqrt{{\frac{u}{{2g}}}} (d) \sqrt{{\frac{{2h}}{g}}}
Ans c
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.



