Video Lecture
Theory For Notes Making
Angular Momentum
Consider a particle P of mass m, having position vector \displaystyle \overrightarrow{r} , rotating about the z-axis. If \displaystyle \overrightarrow{P} is the momentum of the particle , then its angular momentum L is defined as
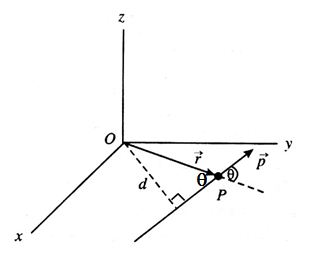
\displaystyle \overrightarrow{L}=\overrightarrow{r}\,\times \,\overrightarrow{p}
The magnitude of angular momentum is
\displaystyle L=r\,p\,\,\sin \theta
and its direction is normal to the plane containing \displaystyle \overrightarrow{r} and \displaystyle \overrightarrow{P}, i.e., along the z-axis in this case.
Simplifying L = P (r sinq) = P.d, where d is perpendicular distance of the line of direction of \displaystyle \overrightarrow{P}. From (O).
If we have a collection of particles or a rigid body, the total angular momentum \displaystyle \overrightarrow{L} will be the vector sum of the angular moment of the individual particles:
Relation between angular momentum, moment of inertia and angular velocity
The angular momentum of a body about a given axis is the sum of moments of linear momenta of the constituent particles of the body about the given axis.
Let {{m}_{1}},{{m}_{2}},\ldots {{m}_{n}} be the masses of the constituent particles of the body. Let {{r}_{1}},{{r}_{2}},\ldots {{r}_{n}} be their respective distances from the axis of rotation. If {{v}_{1}},{{v}_{2}},\ldots {{v}_{n}} be the respective velocity of the particles, then the magnitudes of their linear momenta are {{m}_{1}}{{v}_{1}},{{m}_{2}}{{v}_{2}},\ldots {{m}_{n}}{{v}_{n}} respectively.
Angular momentum of the body about the given axis, L = sum of the moments of momenta of the constituent particles of the body about the given axis.
L=({{m}_{1}}{{v}_{1}}){{r}_{1}}+({{m}_{2}}{{v}_{2}}){{r}_{2}}+\ldots +({{m}_{n}}{{v}_{n}}){{r}_{n}}
If w is the angular velocity of the body about the given axis, then the angular velocity of all the constituent particles will also be w, irrespective of their distances from the axis.
Then, {{v}_{1}}={{r}_{1}}\omega ,{{v}_{2}}={{r}_{2}}\omega ,\ldots ,{{v}_{n}}={{r}_{n}}\omega
∴ L=({{m}_{1}}{{r}_{1}}\omega ){{r}_{1}}+({{m}_{2}}{{r}_{2}}\omega ){{r}_{2}}+\ldots +({{m}_{n}}{{r}_{n}}\omega ){{r}_{n}}
or L={{m}_{1}}r_{1}^{2}\omega +{{m}_{2}}r_{2}^{2}\omega +\ldots +{{m}_{n}}r_{n}^{2}\omega
or L=({{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}+\ldots +{{m}_{n}}r_{n}^{2})\omega
or L=\left( {\sum{{m{{r}^{2}}}}} \right)\omega
But \sum{{m{{r}^{2}}}}=I
Where I is the moment of inertia of the body about the given axis.
\displaystyle L=I\omega
Relation between the torque and angular momentum
We know that \displaystyle \overrightarrow{{L\,}}\,\,=\,\,\overrightarrow{{r\,}}\,\,\times \,\,\overrightarrow{{p\,}}, on differentiating the equation with respect to time we get
\displaystyle \frac{{d\overrightarrow{L}}}{{dt}}\,\,=\,\overrightarrow{{r\,}}\,\,\times \,\,\frac{{d\overrightarrow{p}}}{{dt}}\,\,+\,\,\frac{{d\overrightarrow{r}}}{{dt}}\,\,\times \,\,\overrightarrow{{p\,}}
= \displaystyle \overrightarrow{{r\,}}\,\,\times \,\,\overrightarrow{F}\,\,\,+\,\,\,\overrightarrow{v}\,\,\times \,\,m\overrightarrow{{v\,}} [As \displaystyle \frac{{d\overrightarrow{{p\,}}}}{{dt}}\,\,=\,\,\overrightarrow{{F\,}}\,\,and\,\,\,\overrightarrow{{p\,}}\,\,=\,\,m\overrightarrow{{v\,}}]
= \displaystyle \overrightarrow{{\tau \,}}\,\,+\,\,m\,\,(\overrightarrow{v}\,\times \,\,\overrightarrow{{v\,}}) \displaystyle \overrightarrow{v}\,\,\times \,\overrightarrow{v}\,\,=\,\,0
∴ \displaystyle \overrightarrow{{\tau \,}}\,\,=\,\,\frac{{d\overrightarrow{L}}}{{dt}}
The above equation is also known as Newton’s IInd law of rotation. Hence the time rate of change of angular momentum is equal to net external torque applied an the body.
The simplified form of this equation in the case of pure rotation is,
\displaystyle \overrightarrow{\tau }=\frac{{\overrightarrow{{dL}}}}{{dt}}=\frac{d}{{dt}}(I\overrightarrow{\omega })=\frac{{I\overrightarrow{\omega }}}{{dt}}
= \displaystyle I\overrightarrow{\alpha }
This result is the rotational analogue of Newton’s second law:
\displaystyle \overrightarrow{F}=\frac{{\overrightarrow{{dp}}}}{{dt}}=\frac{d}{{dt}}(m\overrightarrow{v})=\frac{{md\overrightarrow{{{{v}_{{CM}}}}}}}{{dt}}=m\overrightarrow{{{{a}_{{CM}}}}}
Angular Impulse
The product of torque and time is defined as angular impulse. It we know that,
\displaystyle \overrightarrow{\tau }=\frac{{d\overrightarrow{L}}}{{dt}}
or \displaystyle \overrightarrow{\tau }dt=d\overrightarrow{L}
\displaystyle \int\limits_{{\overrightarrow{{{{L}_{1}}}}}}^{{\overrightarrow{{{{L}_{2}}}}}}{{d\overrightarrow{L}}}=\left[ {\overrightarrow{{{{L}_{1}}}}} \right]_{{\overrightarrow{{{{L}_{1}}}}}}^{{\overrightarrow{{{{L}_{1}}}}}}
\displaystyle \int{{\overrightarrow{\tau }}}\,\,(dt)=\overrightarrow{{{{L}_{2}}}}-\overrightarrow{{{{L}_{1}}}}
So, the value of angular impulse is equal to change in angular momentum
The above equation is rotational analogous to impulse momentum equation.
Law of Conservation of Angular Momentum
We know that \displaystyle {{\overrightarrow{\tau }}_{{ext}}}=\frac{{d\overrightarrow{L}}}{{dt}}
if \displaystyle {{\overrightarrow{\tau }}_{{ext}}}=0, then \displaystyle \frac{{\overrightarrow{{dL}}}}{{dt}}=0, which means that \displaystyle \overrightarrow{L} is constant. This leads to the law of conservation of angular momentum.
If the resultant external torque on a system is zero, then the total angular momentum of the system remains constant.
\displaystyle I\overrightarrow{\omega }= constant
This is the rotational analogue of the law of conservation of linear momentum
Applications of the law of conservation of angular momentum
1.
A diver jumping from a spring board perform somersaults in air.
When a diver jumps from spring board, he curls his body by rolling his arms and legs. This decreases moment of inertia and hence increases angular velocity. He then performs somersaults. As the diver is about to touch the surface of water, he stretches out his limbs. By doing so, he increases his moment of inertia, thereby reducing his angular velocity.
2.
A ballet dancer can vary her angular speed by outstretching her arms and legs.
Suppose a ballet dancer is rotating with her legs and arms stretched outwards. When she suddenly folds her arms and brings the stretched leg close to the other leg, her angular velocity increases on account of decrease in moment of inertia.
3.
A man carrying heavy weights in his hands and standing on a rotating table can vary the speed of the table.
Suppose a man is standing on a rotating table with his arms outstretched. Suppose he is holding heavy weights in his hands. When the man suddenly folds his arms, his angular velocity increases on account of the decrease in moment of inertia.
4.
During collision also the angular momentum remains conserved JEE only
Consider a rod which is hinged about an axis passing through (O). A small mass m moving with velocity u strikes at the free end of the rod .So, now we have pure rotational motion of the rod after the collision. As the ball collides with rod, two different collision force acts.
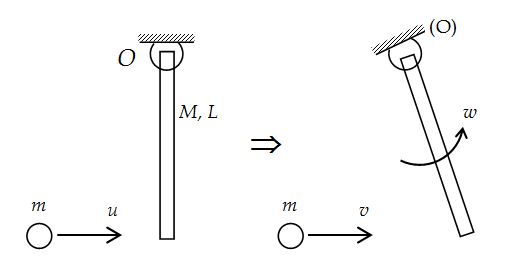
(i) Collision force between mass m and the rod, which is internal force for (mass + rod) system and they cancel out from Newton’s IIIrd Law.
(ii) Reaction force at hinge point (O). For (disc + rod) system this is external force. But about hinge, it’s torque is zero.
So, net external torque on system about hinge is zero. Applying conservation of angular momentum. about hinge (O) for mass + rod system we get,
initial (Lmass + Lrod ) = final (Lmass + Lrod ).
mul + 0 = mvl + (I0w)
mul = mvl + \displaystyle \frac{{M{{l}^{2}}}}{3}w … (i)
For point of impact
coefficient of restitution can be written as \displaystyle e=\frac{{(\omega l)-v}}{u} … (ii)
Solving equation (i) and (ii) we find w & v.
Note : If the rod is not hinged but free then apply conservation of angular momentum about the c.m.
Illustration
A uniform disc of mass M and radius R is rotating with angular speed ω on a smooth horizontal plane as shown.
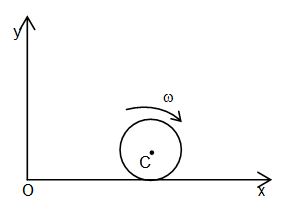
A uniform disc of mass M and radius R is rotating with angular speed w on a smooth horizontal plane as shown.
(a) Find the magnitude and sense of angular momentum about centre of mass .
(b) Find the magnitude and sense of angular momentum about O.
(c) In case disc is rolling with angular speed ω on a horizontal plane as shown, find magnitude of angular momentum about (i) C (ii) O
Solution
Angular momentum about any point,
\displaystyle {{\vec{L}}_{P}}={{\vec{L}}_{{cm}}}+M{{\vec{r}}_{{cm,\,P}}}\times {{\vec{v}}_{{cm}}}
(a) On smooth horizontal plane, only disc is rotating,
so, Lcm = Icmw = \displaystyle \frac{1}{2}M{{R}^{2}}\omega clockwise sense.
(b) same as in part (a)
(c) Lcm = Icmw = \displaystyle \frac{1}{2}M{{R}^{2}}\omega clockwise sense
L0 = Lcm + MRvcm = \displaystyle \frac{1}{2}M{{R}^{2}}\omega +MR\omega R = \displaystyle \frac{3}{2}M{{R}^{2}}\omega clockwise sense.
Illustration
A disc of mass M and radius R is rolling with angular speed w on a horizontal plane as shown. What is the magnitude of angular momentum of the disc about the origin O is
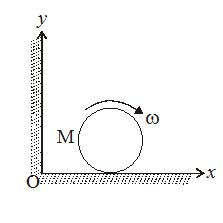
Solutions
From the theorem
\displaystyle \overrightarrow{{{{L}_{0}}}}\,\,=\,\,{{\overrightarrow{L}}_{{com}}}\,\,+\,\,(\overrightarrow{{r\,}}\,\times \,m{{\vec{v}}_{{\text{cm}}}})\, ….(i)
We may write
Angular momentum about O = Angular momentum about COM + Angular momentum of COM about origin
\displaystyle {{L}_{0}}\,\,=\,\,I\,\omega \,\,+\,\,MRv
\displaystyle =\frac{1}{2}\,\,M{{R}^{2}}\,\omega \,\,+\,\,MR\,\,(R\,\omega )
\displaystyle =\frac{3}{2}\,\,M{{R}^{2}}\,\omega
Illusrtation
The disc is freely rotating with an angular speed w on a smooth horizontal plane. It is hooked at a rigid peg P and rotates about P without bouncing. What is its angular speed after the impact.
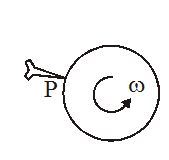
Solution:
During the impact, the impact forces pass through the point P. Therefore, the torque produced by it about P is equal to zero.
Consequently the angular momentum of the disc about P, just before and after the impact remains the same.
L2 = L1 … (i)
where L1 = angular momentum of the disc about P just before the impact
= lw = \displaystyle \frac{1}{2}mr2w.
L2 = angular momentum of the disc about P just after the impact
= Iw = \displaystyle \left( {\frac{1}{2}\ m{{r}^{2}}+m{{r}^{2}}} \right)\ \omega =\frac{3}{2}\ m{{r}^{2}}{\omega }’
\displaystyle \frac{3}{2}\ m{{r}^{2}}{\omega }’=\frac{{m{{r}^{2}}}}{2}\,\omega
\displaystyle {\omega }’=\frac{1}{3}\,\omega
Illustration
A uniform rod AB of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to the end B perpendicular to the length of the rod. The time taken by the rod to turn a angle θ is \frac{{\pi mL}}{{24P}}. Find θ
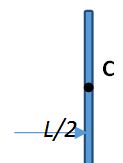
Solution angular impulse = Lf – Li
\frac{{PL}}{2}=\frac{{M{{L}^{2}}\omega }}{{12}}– 0
ω = \frac{{6P}}{{mL}}
θ = ωt = \frac{{6P}}{{mL}}\times \frac{{\pi mL}}{{24P}}=\frac{\pi }{4}
Objective Assignment
1.
Conservation of angular momentum is applicable on a system only if
(a) net external force is zero
(b) net external torque is zero
(c) net external force is non-zero
(d) net external torque is non-zero
Ans (b)
2.
If a man standing in centre of a rotating stool with his arms outstretched lower his hands then his moment of inertia about axis of rotation
(a)increases
(b) decreases
(c) remains same
(d) may increase or decrease
Ans (b)
3.
Angular momentum of a body depends on time with relation \overrightarrow{{L\,}}=(5{{t}^{2}}-5t+5)\hat{k}Nms. Find magnitude of torque at time t = 0
(a) 5 Nm
(b) 10 Nm
(c) 2.5 Nm
(d) none of these
Ans (a)
4.
A particle of mass m is moving along the line y = 3x + 5 with speed V. The magnitude of angular momentum about origin is
(a) \displaystyle \frac{{\sqrt{5}}}{2}mV
(b) \displaystyle \frac{5}{2}mV
(c) \displaystyle \frac{1}{2}mV
(d) \displaystyle \frac{1}{{\sqrt{3}}}mV
Ans (a)
5.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 s-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
(a)3125 J, 62.5 kg m2/s
(b)3125 J, 60.03125 J,
(c) 3125 J, 63.5 kg m2/s
(d)3125 J, 60.5 kg m2/s
Ans (a)
6.
A 40 kg flywheel in the form of a uniform circular disc 200 cm in diameter is making 120 revolutions per minute. Calculate angular momentum.
(a)260.4 kg m2 s-1
(b)251.4 kg m2 s-1
(c)258.4 kg m2 s-1
(d)227.4 kg m2 s-1
Ans (b)
7.
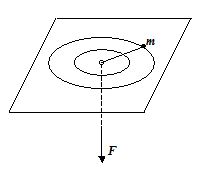
Figure shows a particle of mass m moving in a circle with the centripetal force provided by a rope that passes through a hole in the table. The initial angular momentum is Lo. The force is changed in such a way that the radius of the motion decreases from r1to r2.
(a)
How does the force vary as a function of r?
(a) \frac{{L_{o}^{3}}}{{m{{r}^{3}}}}
(b) \frac{{L_{o}^{-3}}}{{m{{r}^{3}}}}
(c) \frac{{L_{o}^{-2}}}{{m{{r}^{3}}}}
(d) \frac{{L_{o}^{2}}}{{m{{r}^{3}}}}
Ans (d)
(b)
Calculate the work done by the force in changing the radius.
(a) \displaystyle \frac{{L_{o}^{-3}}}{{5m}}\left( {\frac{1}{{r_{2}^{2}}}-\frac{1}{{r_{1}^{2}}}} \right)
(b) \displaystyle \frac{{L_{o}^{2}}}{{2m}}\left( {\frac{1}{{r_{2}^{2}}}-\frac{1}{{r_{1}^{2}}}} \right)
(c) \displaystyle \frac{{L_{o}^{-3}}}{{3m}}\left( {\frac{1}{{r_{2}^{2}}}-\frac{1}{{r_{1}^{2}}}} \right)
(d) \displaystyle \frac{{L_{o}^{2}}}{{2m}}\left( {\frac{1}{{r_{2}^{-2}}}-\frac{-1}{{r_{1}^{-2}}}} \right)
Ans (b)
(c)
What is the change in kinetic energy of the particle?
(a) ΔK = W
(b) ΔK = –W
(c) ΔK = 2W
(d) ΔK =5 W
Ans (a)
(d)
Does the work energy theorem apply?
(a)Yes
(b)Partially Applied
(c) No
Ans (a)
8.
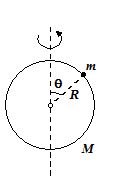
The figure shows a thin ring of mass M = 1 kg and radius R = 0.4m spinning about a vertical diameter. (Take I = 1/2MR2). A small bead of mass m = 0.2 kg can slide without friction along the ring. When the bead is at the top of the ring, the angular velocity is 5 rad/s What is the angular velocity when the bead slips halfway to the horizontal (when Θ = 45o)
(a) 4.50 rad/s
(b) 4.00 rad/s
(c) 5.00 rad/s
(d) 4.16 rad/s
Ans (d)
Subjective Assignment
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
