Video Lecture
Theory For Making Notes
ACCELERATION DUE TO GRAVITY ON THE SURFACE OF EARTH
Consider a mass m placed on the surface of the earth of mass M. The mass experience a force F due to gravitation of earth
where F=G\frac{{Mm}}{{{{R}^{2}}}}
But the force with which a body is attracted towards the Earth gives the weight of the body.
∴ F = mg
∴ mg=G\frac{{Mm}}{{{{R}^{2}}}} or g=\frac{{GM}}{{{{R}^{2}}}}
Variation in acceleration due to gravity with height
Consider a body kept at a height h above the surface of earth. The force of attraction due to the earth on the body is F’. Where F’=G\frac{{Mm}}{{{{{(R+h)}}^{2}}}}but F’=mg’
\displaystyle \therefore mg’=G\frac{{Mm}}{{{{{(R+h)}}^{2}}}}
hence g’=\frac{{GM}}{{{{{(R+h)}}^{2}}}}
we know that at the surface of the earth, g=\frac{{GM}}{{{{R}^{2}}}}
On dividing g’ by g we get
\frac{{g’}}{g}=\frac{{{{R}^{2}}}}{{{{{(h+R)}}^{2}}}}
Hence g’=\frac{{g{{R}^{2}}}}{{{{{(h+R)}}^{2}}}} ——-(i)
( From the above equation we can find gravity at any height)
Variation of gravity with height
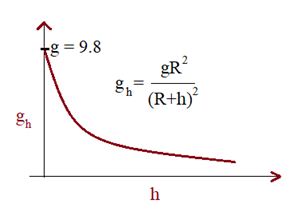
But also we can use an approximation to find gravity at a small height i.e. if h<<R as follows
g’=\frac{{g{{R}^{2}}}}{{{{{(h+R)}}^{2}}}} hence g’=\frac{g}{{{{{\left( {1+\frac{h}{R}} \right)}}^{2}}}}
So, with increase in height, g decreases. If h<<R.
g’=g\,{{\left[ {1+\frac{h}{R}} \right]}^{{-2}}}=g\ \left[ {1-\frac{{2h}}{R}} \right] (Use bionomial approximation)
hence g’=g\ \left[ {1-\frac{{2h}}{R}} \right]
so as height increases gravity decreases linearly for small heights.
Loss in weight at heighth (<<R)
We know that, g’=g\left( {1-\frac{{2h}}{R}} \right)
mg’=mg\left( {1-\frac{{2h}}{R}} \right)=mg-\frac{{2mgh}}{R}
or mg’-mg=\frac{{-2mgh}}{R}
or mg-mg’=\frac{{2mgh}}{R}
loss in weight =\frac{{2mgh}}{R}
Variation in acceleration due to gravity with depth
At the surface of the earth,
g=\frac{{GM}}{{{{R}^{2}}}}
for a point at a depth d below the surface,
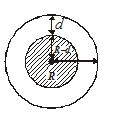
g’=\frac{{GM}}{{{{R}^{3}}}}\ \left[ {R-d} \right] (see video lecture to reach this step)
\frac{{g’}}{g}=\left( {\frac{{R-d}}{R}} \right) i.e., g’= g\ \left[ {1-\frac{d}{R}} \right]
So with increase in depth below the surface of the earth, g decreasing and at the center of the earth it becomes zero as shown in the graph given below.
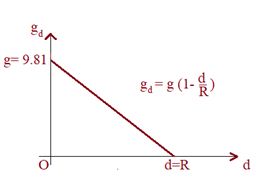
Comparison of height and depth for the same change in ‘g’
As we have seen above, the value of g decreases as we go above the surface of Earth or when we go below the surface of Earth. This can be taken to mean that value of g is maximum on the surface of Earth. hence {{g}_{{\max }}}=\frac{{GM}}{{{{R}^{2}}}}
Now {{g}_{h}}=g\left( {1-\frac{{2h}}{R}} \right)and {{g}_{d}}=g\left( {1-\frac{d}{R}} \right)
When {{g}_{h}}={{g}_{d}},then 1-\frac{{2h}}{R}=1-\frac{d}{R}\ -\frac{{2h}}{R}=-\frac{d}{R}
or 2h=d or d=2h. Take care that this result is applicable for small heights only. Because while deriving the relation {{g}_{h}}=g\left( {1-\frac{{2h}}{R}} \right) we took this assumption that h<<R
Variation in acceleration due to gravity due to rotation of earth and latitude angle
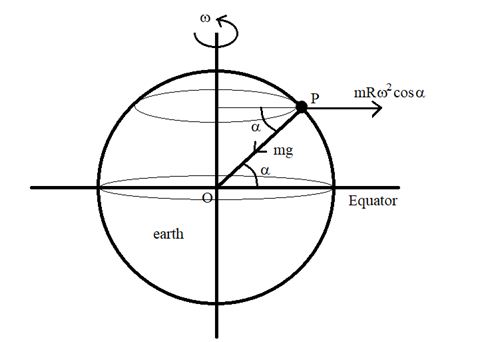
∴The earth is rotating about its axis from west to east. So, the earth is a non-inertial frame of reference. Every body on its surface experiences a centrifugal force mRw2 cosa. Where a is latitude of the place.
The net force on a particle on the surface of the earth is the resultant of these two forces which can be calculated by using law of parallelogram.
F = \sqrt{{{{m}^{2}}{{g}^{2}}+{{m}^{2}}{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha \,+\,2\,(mg)\,(m{{\omega }^{2}}R\cos \alpha )\,[\cos \,(180-\alpha )]}} (the angle between the two forces is 180 -a as clear from the diagram)
This net force produces the weight of the body hence F=mg’ ( where g’ is the net gravity at a latitude a
Therefore, mg’ = \sqrt{{{{m}^{2}}{{g}^{2}}+{{m}^{2}}{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha \,+\,2\,(mg)\,(m{{\omega }^{2}}R\cos \alpha )\,[\cos \,(180-\alpha )]}}
taking m2 as common from RHS and cancelling m from both sides we get g’=\sqrt{{{{g}^{2}}+{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha \,+\,2\,g\,{{\omega }^{2}}R\cos \alpha )\,[\cos \,(180-\alpha )]}}
hence g’=\sqrt{{{{g}^{2}}+{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha \,-\,2\,g\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha )]}}
taking g2 as common on RHS
g’=\sqrt{{{{g}^{2}}\left[ {1+\frac{{{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha }}{{{{g}^{2}}}}\,-\frac{{2\,g\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha }}{{{{g}^{2}}}}\,} \right]}} \Rightarrow g’=g\sqrt{{\left[ {1+\frac{{{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha }}{{{{g}^{2}}}}\,-\frac{{2\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha }}{g}\,} \right]}}
here w is the angular velocity of rotation of earth about its own axis which can be given as
\displaystyle \omega =\frac{{2\pi }}{T}=\frac{{2\pi }}{{24hrs}}=\frac{{2\pi }}{{24\times 60\times 60\sec }}=0.0000727rad/\sec . hence it Is a very small number therefore w4 becomes negligible so the whole term \displaystyle \frac{{{{\omega }^{4}}{{R}^{2}}{{{\cos }}^{2}}\alpha }}{{{{g}^{2}}}} from the above equation of g’ can be neglected hence we get g’=g{{\left[ {1-\frac{{2\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha }}{g}\,} \right]}^{{1/2}}}
again here \displaystyle \frac{{{{\omega }^{2}}R}}{{{{g}^{{}}}}}is a small term so we can use binomial approximation and can write the above equation of g’ as follows
g’=g\left[ {1-\frac{1}{2}\times \frac{{2\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha }}{g}\,} \right]
\Rightarrow g’=g\left[ {1-\frac{{\,{{\omega }^{2}}R{{{\cos }}^{2}}\alpha }}{g}\,} \right]
hence finally we get g’=g-\,{{\omega }^{2}}R{{\cos }^{2}}\alpha \,
Important points to remember
(i) at the pole, a = 90°cos a = minimum = 0 hence g’ is maximum and is equal to g
(ii) at equator a = 0°, so g’ is minimum and is equal to g-w2R
(iii) due to rotation of earth the gravity on the surface is decreased except at poles.
Important data :
Mass of earth We know that g=\frac{{GM}}{{{{R}^{2}}}} or M=\frac{{g{{R}^{2}}}}{G}
Here, R = 6.4 × 106 m, G = 6.67 × 10–11 Nm2 kg–2 and g = 9.8 ms–2 \ M=\frac{{9.8\times 6.4\times {{{10}}^{6}}\times 6.4\times {{{10}}^{6}}}}{{6.67\times {{{10}}^{{11}}}}}\text{kg} =6.018\times {{10}^{{24}}}\text{kg}
| Mean density of earth We know that g=\frac{{GM}}{{{{R}^{2}}}} If r be the mean density of Earth, then M=\frac{4}{3}\pi {{R}^{3}}\rho ∴ g=\frac{G}{{{{R}^{2}}}}\times \frac{4}{3}\pi {{R}^{3}}\rho =\frac{4}{3}\pi GR\rho or \rho =\frac{{3g}}{{4\pi GR}} g=9.8\,\text{m}{{\text{s}}^{{-2}}},G=6.67\times {{11}^{{-11}}}\text{N}{{\text{m}}^{2}}\text{k}{{\text{g}}^{{-2}}}, R=6400\,\text{km}=\text{6}\text{.4}\times \text{1}{{\text{0}}^{\text{6}}}\text{m}
∴ \rho =\frac{{3\times 9.8\times 7}}{{4\times 22\times 6.67\times {{{10}}^{{-11}}}\times 6.4\times {{{10}}^{6}}}}\text{kg}\,{{\text{m}}^{{-3}}} = 5478.4 kg m–3 |
1. Mass of earth =6.018\times {{10}^{{24}}}\text{kg} 2. Mean density of earth= 5478.4 kg m–3 3. Radius of Earth= 6400 km = 6.4 × 106 m |
Example-5:
Calculate the acceleration due to gravity at the surface of Mars if its diameter is 6760 km and mass one tenth that of the earth. The diameter of earth is 12742 km and acceleration due to gravity on the earth is 9.8 m/s2.
Solution:
We know that
g=\frac{{GM}}{{{{R}^{2}}}}
\frac{{{{g}_{M}}}}{{{{g}_{E}}}}=\left( {\frac{{{{M}_{M}}}}{{{{M}_{E}}}}} \right)\,{{\left( {\frac{{{{R}_{E}}}}{{{{R}_{M}}}}} \right)}^{2}}=\left[ {\frac{1}{{10}}} \right]\ {{\left[ {\frac{{12742}}{{6760}}} \right]}^{2}}
or, \frac{{{{g}_{M}}}}{{{{g}_{E}}}}=0.35
gM = 0.35 x gE = 9.8 x 0.35 = 3.48 m/s2
Illustration
A simple pendulum of length one metre is taken to a height R, which is the radius of earth. If the acceleration due to gravity on the surface of earth is p2 m/s2, what is the period of the pendulum at this height?
(a) 1 s (b) 2 s
(c) 3 s (d) 4 s
Solution
As we know that time period of simple pendulum i.e. T = 2\pi \sqrt{{\frac{l}{g}}}
Where g is acceleration due to gravity on the surface of earth and is given as π2 m/s2.
At height R the acceleration due to gravity
i.e g’ = \frac{{{{\pi }^{2}}}}{4} m/s2
∴ T=2\pi \sqrt{{\frac{1}{{\left( {{{\pi }^{2}}/4} \right)}}}}=4s
(d)
Illustration
A planet has twice the density of earth but the acceleration due to gravity on its surface is exactly the same as on the surface of earth. Its radius in terms of earth R will be
(a) R/4
(b) R/2
(c) R/3
(d) R/8
Solution
We have g = \frac{{GM}}{{{{R}^{2}}}}=\frac{G}{{{{R}^{2}}}}\left[ {\frac{4}{3}\pi {{R}^{3}}\rho } \right]
where r is the density of the earth.
For the planet g’ = \frac{G}{{{{{\left( {R’} \right)}}^{2}}}}\left[ {\frac{4}{3}\pi R{{‘}^{3}}\left( {2\rho } \right)} \right]
According to the question
g = g’
\frac{G}{{{{R}^{2}}}}\left[ {\frac{4}{3}\pi {{R}^{3}}\rho } \right]=\frac{G}{{R{{‘}^{2}}}}\times \frac{4}{3}\pi R{{‘}^{3}}\left( {2\rho } \right)
R’ = \frac{R}{2}
(b)
Practice Questions (Basic Level)
1.
Considering the earth to be a homogeneous sphere. Scientist A goes deep down in a mine and scientist B goes high up in a balloon. The gravitational field measured by
(a) A goes on decreasing and that B goes on increasing
(b) Both A and B goes on increasing
(c) B goes on decreasing and that by A goes on increasing
(d) Both A and B goes on decreasing
Ans (d)
2.
As we go from equator to the poles the value of g
(a) remains the same
(b) decreases
(c) increases
(d) decreases upto a latitude of 45° and then increases
Ans (c)
3.
A planet has twice the values of mass and radius of earth. Acceleration due to gravity on the surface of the planet is
(a) 9.8 m/sec2
(b) 4.9 m/sec2
(c) 980 m/sec2
(d) 19.6 m/sec2
Ans (b)
4.
The value of g will be 1% of its value at the surface of earth at a height of (Re= 6400 km)
(a) 6400 km
(b) 57600 km
(c) 2560 km
(d) 64000 km
Ans (b)
5.
The variation of acceleration due to gravity as one moves away from earth centre is given by
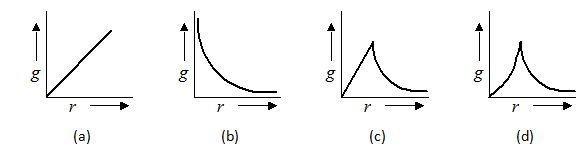
Ans (c)
Practice Questions (JEE Main Level)
1.
If the radius of earth were to shrink by 1% its mass remaining the same, the acceleration due to gravity on the earth’s surface would
(a) increase by 1%
(b) increase by 2%
(c) decrease by 2%
(d) decrease by 1%
Ans (b)
Practice Questions (JEE Advance Level)
1.
Two equal masses m and m are hung from a balance whose scale pans differ in vertical height by h. Calculate the error in weighing, if any, in terms of density of earth r.
(a) \frac{8}{3}\pi \rho Gmh
(b) \frac{-8}{3}\pi \rho Gmh
(c) \frac{5}{3}\pi \rho Gmh
(d) \frac{-5}{3}\pi \rho Gmh
Ans (a)
2.
A body of mass m is raised to a height h (h<<R) from the surface of the earth where the acceleration due to gravity is g. The loss in weight is
(a) \frac{{mgh}}{R}
(b) \frac{{mgh}}{{2R}}
(c) \frac{{2mgh}}{R}
(d) \frac{{mgh}}{{4R}}
Ans (c)
3.
Let be the force acting on particle at a height \left( {\frac{{\sqrt{5}-1}}{2}} \right){{R}_{e}} above the earth’s surface and be the force acting on the same particle at a depth \left( {\frac{{\sqrt{5}-1}}{2}} \right){{R}_{e}} below the earth’s surface then ( = radius of Earth)
(a) {{F}_{a}}>{{F}_{b}}
(b) {{F}_{a}}<{{F}_{b}}
(c) {{F}_{a}}={{F}_{b}}
(d) none of these
Ans (c)
