Video Lecture
Theory For Making Notes
Electric dipole
Two equal and opposite charges separated by a finite distance constitute an electric dipole. If -q and +q are charges at distance 2a apart.
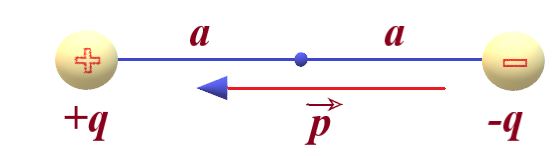
The dipole moment \vec{p} is given as \vec{p}=q\times 2\vec{a} with a direction from negative to positive charge and \left| p \right|=2qa
It has dimension [LTA] and SI unit (coulomb x m) and experimental unit is Debye.
Electric field due to a dipole at axial point
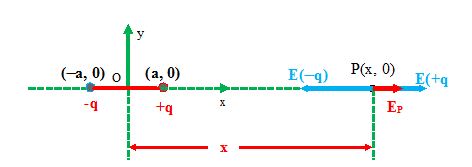
Let the charges (-q) and +q are kept at point (-a, 0) & (a, 0) respectively in xy plane. The electric field at point P(x, 0) will be then the vector sum of the two electric fields produced by the two charges of the dipole
\displaystyle {{\vec{E}}_{{axial}}} = \displaystyle {{\vec{E}}_{{+q}}}+{{\vec{E}}_{{-q}}} = \displaystyle \frac{{Kq}}{{{{{\left( {x-a} \right)}}^{{_{2}}}}}}\hat{i}-\frac{{Kq}}{{{{{\left( {x+a} \right)}}^{2}}}}\hat{i} , where \displaystyle \hat{i} is the unit vector along axis.
\displaystyle =Kq.\frac{{\left( {{{{\left( {x+a} \right)}}^{2}}-{{{\left( {x-a} \right)}}^{2}}} \right)}}{{{{{\left( {{{x}^{2}}-{{a}^{2}}} \right)}}^{2}}}}\hat{i}\stackrel{\scriptscriptstyle\to}=Kq.\frac{{\left( {2x} \right)\left( {2a} \right)}}{{{{{\left( {{{x}^{{_{2}}}}-{{a}^{2}}} \right)}}^{2}}}}\hat{i}
hence \displaystyle {{E}_{{axial}}}=\frac{{2K\vec{p}x}}{{{{{\left( {{{x}^{2}}-{{a}^{2}}} \right)}}^{2}}}}\hat{i}
Special Case
For a short dipole x>>a hence neglecting a from the denominator we get \displaystyle \,{{\vec{E}}_{{axial}}}=\frac{{2K\vec{p}}}{{{{x}^{3}}}}
Note that the net electric field I parallel to the dipole moment
Electric field on equatorial line or perpendicular bisector of dipole
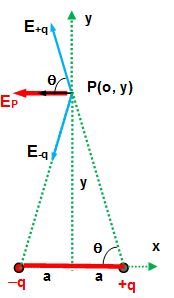
At P there are two electric fields due to two charges of dipole.
\displaystyle {{\vec{E}}_{{+q}}}=\frac{{Kq}}{{\left( {{{y}^{2}}+{{a}^{2}}} \right)}}(-\cos \theta \hat{i}+\sin \theta \hat{j})
\displaystyle {{\vec{E}}_{{-q}}}=\frac{{Kq}}{{\left( {{{y}^{2}}+{{a}^{2}}} \right)}}(-\cos \theta \hat{i}-\sin \theta \hat{j});
The net electric field \displaystyle \,\,{{\vec{E}}_{P}} is the sum of the two vectors hence
\displaystyle \,\,{{\vec{E}}_{P}}={{\vec{E}}_{{+q}}}+{{\vec{E}}_{{-q}}}=\frac{{-2Kq}}{{\left( {{{y}^{2}}+{{a}^{2}}} \right)}}\cos \theta \hat{i}
\displaystyle \Rightarrow {{\vec{E}}_{p}}=-2\left[ {\frac{{Kq}}{{{{y}^{2}}+{{a}^{2}}}}} \right].\frac{a}{{{{{\left( {{{a}^{2}}+{{y}^{2}}} \right)}}^{{{}^{1}\!\!\diagup\!\!{}_{2}\;}}}}}\hat{i}
\displaystyle ={\leftarrow}\stackrel{\scriptscriptstyle\to}{\leftarrow}\frac{{-K\left( {2aq} \right)}}{{{{{\left( {{{y}^{2}}+{{a}^{2}}} \right)}}^{{{}^{3}\!\!\diagup\!\!{}_{2}\;}}}}}\hat{i}
\frac{{-K\vec{p}}}{{{{{({{y}^{2}}+{{a}^{2}})}}^{{3/2}}}}}
Electric field at any point due to a short dipole
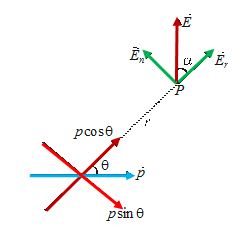
Consider a dipole of moment \vec{p} and P is a point at distance r where field is required. Now, the \vec{p} has two components p\cos \theta and p\sin \theta . The point P is an axial point for the former and is an equatorial point for the later component. Therefore, the radial component of field at P due to p\cos \theta component is
{{E}_{r}}=\frac{{2kp\cos \theta }}{{{{r}^{3}}}} …(i)
and the normal component of field at P due to p\sin \theta component is
{{E}_{n}}=\frac{{kp\sin \theta }}{{{{r}^{3}}}} …(ii)
Squaring of (i) and (ii) and adding then
E=\frac{{kp}}{{{{r}^{3}}}}\sqrt{{4{{{\cos }}^{2}}\theta +{{{\sin }}^{2}}\theta }}
E=\frac{{kp}}{{{{r}^{3}}}}\sqrt{{3{{{\cos }}^{2}}\theta +1}}
\tan \alpha =\frac{{{{E}_{n}}}}{{{{E}_{r}}}}=\frac{1}{2}\tan \theta
Dipole in electric field
When a dipole is placed in a uniform field as shown in figure. The net force on it is zero.
Force, F=q\,\,E is acting on each charge but in opposite direction so they form a couple.
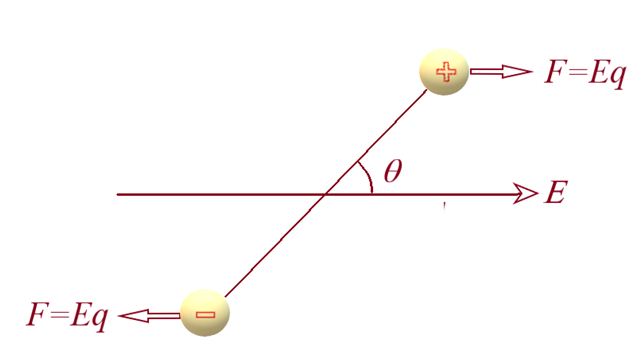
Net torque = moment of the couple
= Force x arm of couple
=qE\times 2a\sin \theta
\tau =pE\sin \theta
\because \,\,\,\,\,\vec{\tau }=\vec{p}\times \vec{E}
Note
(i)
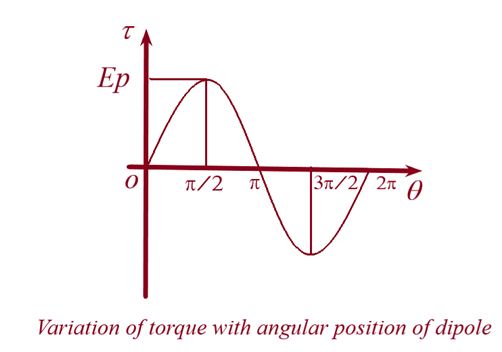
when \theta =0, \tau =0 ,it is called the stable equilibrium position of dipole
(ii)
when \theta =90{}^\circ , torque is maximum and given by {{\tau }_{{\max }}}=PE
(iii)
when \theta =180{}^\circ , \tau =0 , it is called unstable equilibrium position of dipole
Work done in rotating a dipole in uniform field
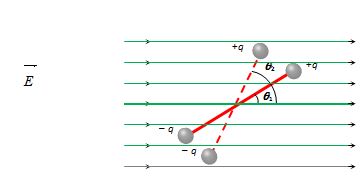
Let a dipole is placed in an electric field at an initial angle θ1. It is to be rotated to a new position where it makes an angle θ2 with the electric field. Now let us rotate the dipole through a small angle d\theta . If dW be the work done, it will be given as dW=\tau \,\,d\,\,\theta
to get the total work done we integrate it sd follows
\int{{dW}}=\int_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}{{\,pE\sin \theta \,\,d\theta }}
W=-pE[\cos {{\theta }_{1}}-\cos {{\theta }_{2}}]
if {{\theta }_{1}}=0 and {{\theta }_{2}}=\theta , then W=pE[1-\cos \theta ]
{{W}_{{\min }}}=0 , when \theta =0 i.e., dipole is parallel to the field.
{{W}_{{\max }}}=2PE when \theta =180{}^\circ i.e., dipole is antiparallel to the field.
When electric field is non-uniform net force on dipole is non-zero.
Potential Energy: In case of a dipole, potential energy of dipole is defined as work done in rotating a dipole from a direction perpendicular to the fieldto the given direction, e.,
If {{\theta }_{1}}=90{}^\circ ,\,\,{{\theta }_{2}}=\theta
U=PE(0-\cos \theta )
i.e., U=-pE\cos \theta =-\vec{p}\,.\vec{E}
The potential energy of a dipole in an external field is given by
\displaystyle U=-\vec{p}\,.\,\vec{E}
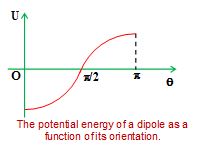
The potential energy as a function of the angle q is shown in Figure the minimum potential energy occurs at q = 0, and the maximum at q = p. The dipole is in stable equilibrium at q = 0. If it is allowed to rotate, it oscillates about the direction of the field.
Force acting on a dipole in an External Non-uniform field.
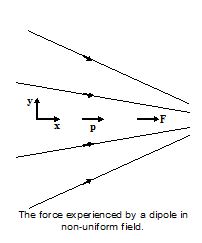
The charges of a dipole experience unequal forces, therefore, the net force on the dipole is not equal to zero. The magnitude of the force is given by the negative derivative of the potential energy with respect to distance along the axis of the dipole.
F = \displaystyle -\frac{{dU}}{{dx}}
= – \displaystyle p.\frac{{dE}}{{dx}}
Illustration
A dipole is formed by two charges of 5μC and -5μC at a distance of 8 mm. Find electric field at
(a) a point 25 cm away from dipole centre at its axis.
(b) a point 20 cm away on its a line perpendicular to the axis and passing through its centre
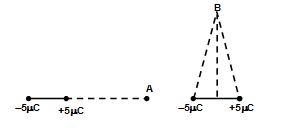
Solution:
(a)
E = \displaystyle \frac{{2p}}{{4\pi {{\varepsilon }_{0}}{{r}^{3}}}} = \displaystyle \frac{{2\times 5\times {{{10}}^{{-6}}}\times 8\times {{{10}}^{{-3}}}\times 9\times {{{10}}^{9}}}}{{{{{\left( {25} \right)}}^{3}}\times {{{10}}^{{-6}}}}} = 4.6 x 104 N/C
(b)
E = – \displaystyle \frac{p}{{4\pi {{\varepsilon }_{0}}{{r}^{3}}}} = \displaystyle -\frac{{5\times {{{10}}^{{-6}}}\times 8\times {{{10}}^{{-3}}}\times 9\times {{{10}}^{9}}}}{{{{{\left( {20} \right)}}^{3}}\times {{{10}}^{{-6}}}}} = – 4.5 x 104 N/C
Illustration
Two tiny spheres, each of mass M, and charges +q and -q respectively, are connected by a massless rod of length, L. They are placed in a uniform electric field at an angle q with the \vec{E} (q» 0o). Calculate the minimum time in which the system aligns itself parallel to the \vec{E}
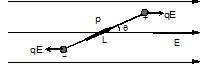
τ = pE sin θ, (as θ → 0,sin θ → θ)
τ = -(pE)q (If we assume angular displacement to be anti-clockwise, torque is clockwise)
a = \displaystyle -\left( {\frac{{pE}}{I}} \right)\theta =-ω2θ
As torque is proportional to ‘θ’ and oppositely directed, there will be an S.H.M.
Here, p = qL and moment of inertia,
I = M (L/2)2 + M (L/2)2 = ML2/2
\displaystyle \therefore \,\,\,\text{Time period,}\stackrel{\scriptscriptstyle\to}{\leftarrow}\text{ T = }2\pi \sqrt{{\frac{I}{{pE}}}}
The minimum time required to align itself along electric field is \displaystyle \frac{T}{4}
Practice Questions (Basic Level)
Q. 1
An electric dipole placed in a uniform electric field experiences, in general
(a) a force and a torque
(b) a force only
(c) a torque only
(d) neither a force nor a torque
Ans. (c)
Q.2
A and B are two points on the axis and the perpendicular bisector respectively of an electric dipole. And B are far away from the dipole and at equal distances from it. The fields at A and B are A and B.
(a) A = B
(b) A=2B
(c) A=-2B
(d) |EB|=1/2|EA|, and B perpendicular to A
Ans. (c)
Q.3
an electric dipole of moment is placed in a uniform electric field , with parallel to . It is then rotted by an angle q. The work done is
(a) pE sin q
(b) pE cosq
(c) pE(1-cosq)
(d) pE(1-sin T)
Ans. (c)
Q. 4
In which of the following states is the potential energy of an electric dipole maximum ?

Ans (a)
Q.5
An electric dipole of moment p is placed normal to the lines of force of electric field E, then the work done in deflecting it through an angle of 180 degrees is
(1) pE
(2) + 2pE
(3) –
(4) Zero
Ans. (4)
Q.6
An electric dipole is placed in an uniform electric field such that the dipole moment makes an angle b ( ¹ 0) with The force and torque acting on the dipole are respectively given by
(1) \displaystyle 0,\,\,\overrightarrow{{p\,}}\times \overrightarrow{{E\,}}
(2) \displaystyle \overrightarrow{{p\,}}\cdot \overrightarrow{{E\,}},\,\,\,\overrightarrow{{p\,}}\times \overrightarrow{{E\,}}
(3) \displaystyle \overrightarrow{{p\,}}\times \overrightarrow{{E\,}},\,\,0
(4) \displaystyle \overrightarrow{{p\,}}\times \overrightarrow{{E\,}},\,\,\overrightarrow{{E\,}}\times \overrightarrow{{p\,}}
Ans. (1)
Q.7
An electric dipole is put in north-south direction in a sphere filled with water. Which statement is correct?
(1) Electric flux is coming towards sphere
(2) Electric flux is coming out of sphere
(3) Electric flux entering into sphere and leaving the sphere are same
(4) Water does not permit electric flux to enter into sphere.
Ans. (3)
Practice Questions (JEE Main Level)
Q.1
An electric dipole is placed at the orgin and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to the y-axis. OP makes an angle q with the x-axis,
(a) tan q=Ö3 (b) tan q= Ö2 (c) q= 45° (d) tan q=1/Ö2
Ans. (b)
Q.2
Electric charges q, q and -2q are placed at the corners of an equilateral triangle ABC of side L. The magnitude of electric dipole moment of the system is
(A) qL (B) 2qL (C) (Ö3)qL (D) 4qL
Ans. (C)
Q.3
An electric dipole is kept in non-uniform electric field. It experiences
(a) A force and a torque
(b) A force but not a torque
(c) A torque but not a force
(d) Neither a force nor a torque
Ans. (a)
Q.4
Three electric charges 2q each are placed at the corners of an equilateral triangle ABC of side l. Another charge -6q is placed at the centroid of the triangle. The magnitude of electric dipole moment of the system is
(a) q
(b) 2ql
(c) \displaystyle \sqrt{3}ql
(d) zero
Ans. (d)
Q.5
If the magnitude of intensity of electric field at a distance x on axial line and at a distance y on equatorial line on a given dipole are equal, then x : y is
(a) 1 : 1
(b) \displaystyle 1:\sqrt{2}
(c) 1 : 2
(d) \displaystyle \sqrt[3]{2}:1
Ans. (d)
Q.6
For a dipole \displaystyle q=2\times {{10}^{{-6}}}C and d = 0.01 m. Calculate the maximum torque for this dipole if \displaystyle E=5\times {{10}^{5}}N/C
(a) \displaystyle 1\times {{10}^{{-3}}}N{{m}^{{-1}}}
(b) \displaystyle 10\times {{10}^{{-3}}}N{{m}^{{-1}}}
(c) \displaystyle 10\times {{10}^{{-3}}}Nm
(d) \displaystyle 1\times {{10}^{2}}N{{m}^{2}}
Ans. (c)
Q.7
An electric dipole is placed along the x-axis at the origin O. A point P is at a distance of 20cm from this origin such that OP makes an angle \displaystyle \frac{\pi }{3} with the x-axis. If the electric filed at P makes an angle θ with x-axis, the value of θ would be
(a) \displaystyle \frac{\pi }{3}
(b) \displaystyle \frac{\pi }{3}+{{\tan }^{{-1}}}\left( {\frac{{\sqrt{3}}}{2}} \right)
(c) \displaystyle \frac{{2\pi }}{3}
(d) \displaystyle {{\tan }^{{-1}}}\left( {\frac{{\sqrt{3}}}{2}} \right)
Ans. (b)
Q.8
Two electric dipoles of moment P and 64 P are placed in opposite direction on a line at a distance of 25 cm. The electric field will be zero at point between the dipoles whose distance from the dipole of moment P is
(a) 5 cm
(b) \displaystyle \frac{{25}}{9}cm
(c) 10 cm
(d) \displaystyle \frac{4}{{13}}cm
Ans. (a)
Q.9
Two short dipoles \displaystyle p\,\hat{k} and \displaystyle \frac{p}{2}\,\hat{k} are located at (0, 0, 0) & (1m, 0, 2m) respectively. The resultant electric field due to the two dipoles at the point (1m, 0, 0) is
(a) \displaystyle \frac{{9p}}{{32\,\pi \,{{\varepsilon }_{0}}}}\,\hat{k}
(b) \displaystyle \frac{{-7p}}{{32\,\pi \,{{\varepsilon }_{0}}}}\,\hat{k}
(c) \displaystyle \frac{{7p}}{{32\,\pi \,{{\varepsilon }_{0}}}}\,\hat{k}
(d) None of these
Ans. (b)
Q.10
An electric dipole is kept on the axis of a uniformly charged ring at distance from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
(a) \displaystyle \frac{{p\,Q}}{{3\,\pi \,{{\varepsilon }_{0}}\sqrt{3}\,{{R}^{2}}}}
(b) \displaystyle \frac{{4p\,Q}}{{3\,\pi \,{{\varepsilon }_{0}}\sqrt{3}\,{{R}^{2}}}}
(c) \displaystyle \frac{{p\,Q}}{{3\,\pi \,{{\varepsilon }_{0}}\,{{R}^{2}}}}
(d) zero
Ans. (d)
Q.11
The force acting between two dipoles is proportional to xn . Where x is their mutual distance and n is
(a) -4 (b) -3 (c) 4 (d) -2
Ans. (a)
Q.12
In which of the following states is the potential energy of an electric dipole maximum ?
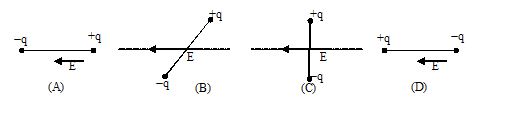
Ans. (a)
Q.13
Two connected charges of +q and -q respectively are at fixed distance AB apart in a non uniform electric field whose lines of force are shown in the figure
The resultant effect on the two charges is
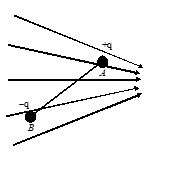
(A) a torque vector in the plane of the paper and no resultant force.
(B) a resultant force in the plane of the paper and no torque.
(C) a torque vector normal to the plane of the paper and no resultant force.
(D) a torque vector normal to the plane of the paper and a resultant force in the plane of the paper.
Ans. (d)
Q.14
We have two electric dipoles. Each dipole consists of two equal and opposite point charges at the end of an insulating rod of length d. The dipoles are placed along the x‑axis at a large distance r apart oriented as shown. The dipole on the left
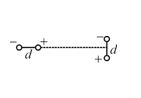
(a) will feel a force upwards and a torque trying to make it rotate clockwise.
(b) will feel a force upwards and a torque trying to make it rotate counterclockwise.
(c) will feel a force upwards and no torque about its centre.
(d) will feel a force downwards and a torque trying to make it rotate clockwise.
Ans. (b)
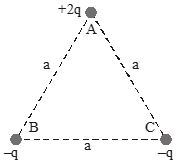
Q.15
Three charges of (+2q), (–q) and (–q) are placed at the corners A, B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
(a) \displaystyle qa
(b) Zero
(c) \displaystyle qa\sqrt{3}
(d) \displaystyle \frac{2}{{\sqrt{3}}}qa
Ans. (c)
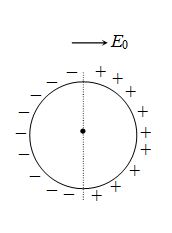
16.
Half part of ring is uniformly positively charged and other half is uniformly negatively charged. Ring is in equilibrium in uniform electric field as shown and free to rotate about an axis passing through its centre and perpendicular to plane. The equilibrium is
(a) stable
(b) unstable
(c) neutral
(d) can be stable or unstable
Ans (a)
17.
The magnitude of electric field intensity at point B (2, 0, 0) due to a dipole of dipole moment, \vec{P}=\hat{i}+\sqrt{3}\hat{j}kept at origin is (assume that the point B is at large distance from the dipole and k=\frac{1}{{4\pi {{\varepsilon }_{0}}}})
(a) \displaystyle \frac{{\sqrt{{13}}k}}{8}
(b) \frac{{\sqrt{{13}}k}}{4}
(c) \frac{{\sqrt{7}k}}{8}
(d) \frac{{\sqrt{7}k}}{4}
Ans (c)
18.
A dipole of dipole moment p is kept at the centre of a ring of radius R and charge q. The dipole moment has direction along the axis of the ring. The resultant force on the ring due to the dipole is
(a) zero
(b) \frac{{pq}}{{4\pi {{\varepsilon }_{0}}{{R}^{3}}}}
(c) \frac{{pq}}{{2\pi {{\varepsilon }_{0}}{{R}^{3}}}}
(d) \frac{{pq}}{{4\pi {{\varepsilon }_{0}}{{R}^{3}}}}only if the charge is uniformly distributed on the ring.
Ans (b)
Comprehension Based Questions (19 and 20)
A dipole consists of two point charges ±2 nC separated by 4 cm.
19.
What is the dipole moment ?
(i) 9 x 10–11 C-m
(ii) 8 x 10–11 C-m
(iii) 6 x 10–11 C-m
(iv) 3 x 10–11 C-m
Ans (ii)
20.
What is the change in potential energy when the dipole rotates from alignment along a field E =105 N/C to an orientation 90° to E?
(i) 2 x 10–6 J
(ii) 8 x 10–6 J
(iii) 10 x 10–6 J
(iv) 5 x 10–6 J
Ans (ii)
Practice Questions (JEE Advance Level)
Q.1
Imagine a dipole is at the centre of a spherical surface. If magnitude of electric field at a certain point on the surface of sphere is 10 N/C, then which of the following cannot be the magnitude of electric field anywhere on the surface of sphere
(a) 4 N/C (b) 8 N/C (c) 16 N/C (d) 18 N/C
Ans. (a)
Q.2
Two positive point charges are kept along x-axis on each side of origin in x-y plane at An electric dipole of length a is kept along y-axis with its mid point at origin such that its dipole moment is along +ve y-axis. The dipole is released from given position then
(a) the dipole will vibrate in SHM along y-axis with mean position at origin
(b) the dipole will move linearly along +y axis
(c) the dipole will be in rotational as well as translation motion
(d) the dipole will oscillate on y-axis
Ans. (b)
Q.3
A non-conducting ring of mass m and radius r is lying at rest in the vertical xy plane on a smooth non-conducting horizontal xy plane. Charges +q and –q are distributed uniformly on the ring. On the two sides of the vertical diameter of the ring, a constant and uniform electric field \displaystyle \vec{E} is set up along the x-direction. The ring is given a small rotation about the vertical diameter of the ring and released. Find the period of oscillation of the ring.
(a) \displaystyle 2\pi \sqrt{{\frac{{mr}}{{4qE}}}}
(b) \displaystyle 2\omega \sqrt{{\frac{{mr}}{{10qE}}}}
(c) \displaystyle 2\mu \sqrt{{\frac{{mr}}{{4qE}}}}
(d) \displaystyle 2\pi \sqrt{{\frac{{mr}}{{16qE}}}}
Ans (a)
4.
An electric dipole is placed along the x-axis at the origin O. A point P is at a distance of 20cm from the origin such that OP makes an angle \frac{\pi }{3} with the x-axis. If the electric field at P makes an angle q with the positive direction of x-axis, the value of q would be
(a) \frac{\pi }{3}
(b) \frac{\pi }{3}+{{\tan }^{{-1}}}\left( {\frac{{\sqrt{3}}}{2}} \right)
(c) \frac{{2\pi }}{3}
(d) {{\tan }^{{-1}}}\left( {\frac{{\sqrt{3}}}{2}} \right)
Ans (b)
Comprehension Based Question (5 and 6)
The figure shows a combination of charges called an electric quadrupole. Find the electric field strength
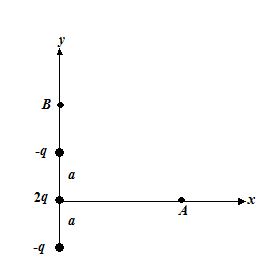
5.
At point A at (r, 0) and
(a) \frac{{2kq}}{{{{r}^{2}}}} \left[ {5-{{{\left( {2+\frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{-3/2}}}} \right]
(b) \frac{{2kq}}{{{{r}^{2}}}} \left[ {3-{{{\left( {5+\frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{-3/2}}}} \right]
(c) \frac{{2kq}}{{{{r}^{2}}}} \left[ {9-{{{\left( {3+\frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{-3/2}}}} \right]
(d) \frac{{2kq}}{{{{r}^{2}}}} \left[ {1-{{{\left( {1+\frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}}^{{-3/2}}}} \right]
Ans (d)
6.
At point B at (0, r)
(a) \frac{{5kq{{a}^{3}}({{a}^{2}}-3{{r}^{2}})}}{{{{r}^{2}}{{{({{r}^{2}}-{{a}^{2}})}}^{2}}}}
(b) \frac{{9kq{{a}^{2}}({{a}^{5}}-3{{r}^{2}})}}{{{{r}^{2}}{{{({{r}^{2}}-{{a}^{5}})}}^{2}}}}
(c) \frac{{2kq{{a}^{2}}({{a}^{2}}-3{{r}^{2}})}}{{{{r}^{2}}{{{({{r}^{2}}-{{a}^{2}})}}^{2}}}}
(d) \frac{{2kq{{a}^{2}}({{a}^{2}}-3{{r}^{2}})}}{{{{r}^{2}}{{{({{r}^{4}}-{{a}^{4}})}}^{4}}}}
Ans (c)
