Video Lecture
Theory For Making Notes
Gauss Theorem
The statement of the Gauss’s law may be written as follows :
The flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ε0. In symbols,
\displaystyle \oint\limits_{{surface}}{{\overrightarrow{E}\,\cdot \,\overrightarrow{{dS}}}}\,\,=\,\,\frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}} …(i)
where qin is the net charge enclosed by the surface through which the flux is calculated.
It should be carefully noted that the electric field on the left-hand side of equation (i) is the resultant electric field due to all the charges existing in the space, whereas, the charge appearing on the right-hand side includes only those which are inside the closed surface.
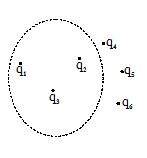
For example for the situation show in diagram the Guass’s law can be written as
\displaystyle \oint{{(\overrightarrow{{{{E}_{1}}}}+}}\overrightarrow{{{{E}_{2}}}}+\overrightarrow{{{{E}_{3}}}}+\overrightarrow{{{{E}_{4}}}}+\overrightarrow{{{{E}_{5}}}}+\overrightarrow{{{{E}_{6}}}})\,\,\cdot \,\,\overrightarrow{{dS}}\,\,\,=\,\,\frac{{{{q}_{1}}+{{q}_{2}}+{{q}_{3}}}}{{{{\varepsilon }_{0}}}}
What is the total flux produced by a charge?
Consider a charge q . Construct a spherical surface around it with charge at the center. Now the flux passing through the spherical surface is same as that produced by the charge.
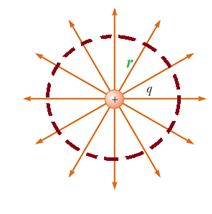
The flux passing through the spherical surface can be calculated using the equation \displaystyle \phi =EA\cos \theta .
hereE is the electric field produced by the charge hence \displaystyle E=\frac{{kq}}{{{{r}^{2}}}},
A is the surface area of the sphere hence \displaystyle A=4\pi {{r}^{2}}
andq =0 as the electric field is radial hence it is along the normal to the surface.
So \displaystyle \phi =\frac{{kq}}{{{{r}^{2}}}}.4\pi {{r}^{2}}.\cos (0)=kq4\pi
\displaystyle \Rightarrow \phi =\frac{1}{{4\pi {{\varepsilon }_{o}}}}q4\pi
hence \displaystyle \phi =\frac{q}{{{{\varepsilon }_{o}}}} This is the flux passing through the spherical surface and actually it is produced by the charge q place at the center. So we conclude that a charge q produce a total flux equal to \displaystyle \frac{q}{{{{\varepsilon }_{o}}}}.
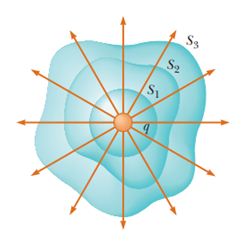
Hence if a charge is surrounded by a number of closed surfaces of any shape as shown then the flux passing through every surface is equal to that produced by the charge i.e. \displaystyle \frac{q}{{{{\varepsilon }_{o}}}}.
Application of Gauss’s Law
Using Gauss’s law in some cases with symmetry arguments, we can derive several important results in electrostatic situations. (For detailed derivation please see the video lectures)
1.
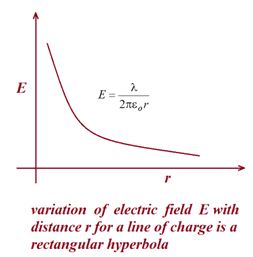
The electric field at any point due to an infinite line of charge with uniform linear charge density λ is perpendicular to the line of charge and has magnitude
E=\frac{\lambda }{{2\pi {{\varepsilon }_{o}}r}} (line of charge)
wherer is the perpendicular distance from the line of charge to the point.
2.
The electric field due to an infinite nonconducting sheet with uniform surface charge density σ is perpendicular to the plane of the sheet and has magnitude
E=\frac{\sigma }{{2{{\varepsilon }_{o}}}} (sheet of charge)
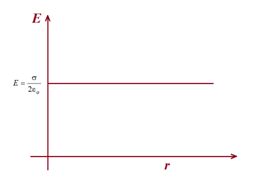
Note that this electric field does not depend on the distance r from the sheet,hence it is a constant.
3.
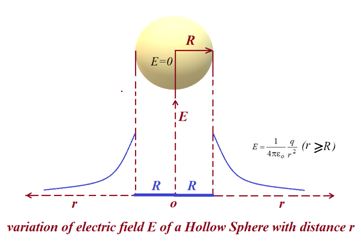
The electric field outside a spherical shell of charge with radius R and total charge q is directed radially and has magnitude
E=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{q}{{{{r}^{2}}}} (spherical shell, for r ≥ R).
Here r is the distance from the center of the shell to the point at which E is measured. (The charge behaves, for external points, as if it were all located at the center of the sphere). The field inside a uniform spherical shell of charge is exactly zero.
E=0 (spherical shell, for r<R).
4.
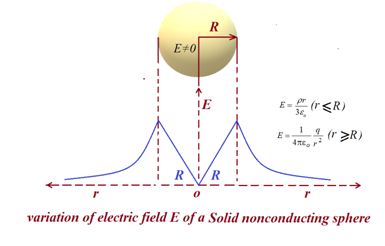
The electric field inside a uniformly charged non conducting sphere is directed radially and has magnitude
E=\left( {\frac{q}{{4\pi {{\varepsilon }_{o}}{{R}^{3}}}}} \right)r=\frac{{\rho r}}{{3{{\varepsilon }_{o}}}}
whereas outside it is given as E=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{q}{{{{r}^{2}}}}
Illustration
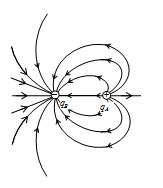
The electric field of two point charges separated by 4.14 cm is as shown in figure (a) What is the nature of charges? (b) What is the ratio of magnitude of charges? (c) Is the field uniform ? (d) Apart from infinity where is the neutral point?
Solution
(a) As lines of force are starting from A and terminating on B, A is positive charge while B negative charge
(b) As number of lines of force emerging or terminating on a charge is proportional to its magnitude.
\displaystyle \left| {\frac{{{{q}_{A}}}}{{{{q}_{B}}}}} \right|\,\,=\,\,\frac{{12}}{6}\,\,=\,\,\frac{2}{1}\, i.e. \displaystyle \left| {{{q}_{A}}} \right|\,\,=\,\,2|\,\,{{q}_{B}}\,|\,
(c) As the lines of force are not equidistant straight lines, the field is not uniform.
(d) As charge \displaystyle {{q}_{A}} is positive while \displaystyle {{q}_{B}} negative neutral point cannot be between them. So if neutral point is at a distance x from B on the line AB.
them. So if neutral point is at a distance x from B on the line AB.
\displaystyle \frac{{{{q}_{A}}}}{{{{{(d+x)}}^{2}}}}\,\,+\,\,\frac{{{{q}_{B}}}}{{{{x}^{2}}}}\,\,=\,\,0 or \displaystyle \frac{{2{{q}_{B}}}}{{{{{(4.14+x)}}^{2}}}}\,\,=\,\,\frac{{{{q}_{B}}}}{{{{x}^{2}}}}
Or \displaystyle \sqrt{2}\,\,(x)\,\,=\,\,(4.14\,+\,x) or x = 10 cm
i.e., neutral point is at C such that BC = 10 cm
Illustration
A spherical shell of radius a is placed in a uniform electric field \displaystyle \vec{E}. Find the amount of flux entering into the shell
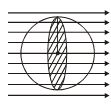
Solution
It is the shaded circular area or projected area of shell which is intercepting the flux hence flux entering depends on this area
Φ = E . S = E .πa^2
Illustration
Derive Gauss’ law from Coulomb’s law.
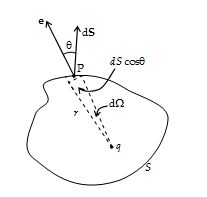
Solution
Let us consider a point charge q inside an arbitrary closed surface S.
The electric field due to q at the position of a differential element \displaystyle d\overrightarrow{S} is given by
\displaystyle \overrightarrow{E}=\frac{q}{{4\pi {{\in }_{0}}{{r}^{2}}}}\hat{e}
where \displaystyle \hat{e} is the unit vector pointing radially outwards from the charge
The flux through \displaystyle d\overrightarrow{S} is given by
\displaystyle d\Phi =\overrightarrow{E}.d\overrightarrow{S}=\frac{q}{{4\pi {{\in }_{0}}{{r}^{2}}}}\hat{e}.d\overrightarrow{S}=\frac{q}{{4\pi {{\in }_{0}}}}\frac{{dS\cos \theta }}{{{{r}^{2}}}}=\frac{q}{{4\pi {{\in }_{0}}}}d\Omega
Thus, \displaystyle \Phi =\int{{d\Phi }}=\frac{q}{{4\pi {{\in }_{0}}}}\int{{d\Omega }}=\frac{I}{{4\pi {{\in }_{0}}}}[4\pi ]\,\,=\,\,\frac{q}{{{{\in }_{0}}}}
Illustration
Determine the field at a point distant r from a uniformly charged plane with surface charge density σ.
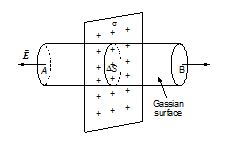
Solution
By symmetry, we conclude the \displaystyle \overrightarrow{E} can only be normal to the charged plane. Also, at points A and B, symmetric with respect to the plane, \displaystyle \overrightarrow{E} should have same magnitude but opposite directions. Hence, a right cylinder is chosen as Gaussian surface.
The flux through the lateral surface is zero. If ΔS is the area of each end face,the total flux is
ΔΦ = EΔS + EΔS = 2EΔS.
Then according to Gauss’s Law,
2EΔS = \frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}}\text{ }=\text{ }\frac{{\sigma \Delta S}}{{{{\varepsilon }_{0}}}}
\displaystyle E=\frac{\sigma }{{2{{\varepsilon }_{0}}}}
Illustration
A uniform positive charge density r (charge per unit volume) exists throughout a spherical volume of radius R. Find the electric field (a) outside the sphere and (b) inside the sphere. Also show how electric field varies as the distance of the point from the centre increases from zero to infinite.
Solution
By symmetry, we conclude that the field \displaystyle \overrightarrow{E} can only be radially outward, both inside and outside the sphere. Moreover, for a given value of r, \displaystyle \overrightarrow{E} has the same magnitude everywhere. To match this symmetry, we choose a Gaussian surface in the form of a sphere of radius r, centred on the spherical volume.
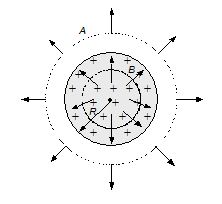
(a)
For any point outside the sphere, r > R :
The total charge inside the spherical volume (surface A) is
\displaystyle Q=\int{{\rho dV}}=\rho \left( {\frac{4}{3}\pi {{R}^{3}}} \right) …(i)
Applying Gauss’s Law,
\oint{{\vec{E}.d\vec{S}}} = \frac{{{{q}_{{\text{in}}}}}}{{{{\varepsilon }_{0}}}}
\displaystyle E(4\pi {{r}^{2}})=\frac{Q}{{{{\varepsilon }_{0}}}}
or \displaystyle E=\frac{Q}{{4\pi {{\varepsilon }_{0}}{{r}^{2}}}} …(ii)
This is just the inverse-square-law field for a point charge Q. In fact, this result is valid for any charged sphere, whether solid or hollow, conducting or non-conducting. The sphere behaves as if whole charge is concentrated at its centre. We can express the result of Eqn.(ii) in terms of the given parameters by using Eqn. (i),
\displaystyle E=\frac{Q}{{4\text{ }\pi {{\varepsilon }_{0}}{{r}^{2}}}}=\frac{1}{{4\text{ }\pi {{\varepsilon }_{0}}{{r}^{2}}}} \rho \left( {\frac{4}{3}\pi {{R}^{3}}} \right)=\frac{{\rho {{R}^{3}}}}{{3\text{ }{{\varepsilon }_{0}}}} \frac{1}{{{{r}^{2}}}}
i.e. E ∝ \displaystyle \frac{1}{{{{r}^{2}}}}
(b)
For any point inside the sphere (r<R) :
We now choose a Gaussian surface B, so that r<R. The charge inside this sphere is
\displaystyle {{q}_{{in}}} = \int\limits_{0}^{r}{{\rho dV}} = \rho \left( {4\text{/3 }\pi {{r}^{3}}} \right)
Applying Gauss’s law,
\displaystyle \oint{{\overrightarrow{E}\,\,.\,\,d\overrightarrow{S}}} = \frac{{{{q}_{{in}}}}}{{{{\varepsilon }_{0}}}}
or \displaystyle E(4\text{ }\pi \text{ }{{r}^{2}})\text{ }=\text{ }\frac{{4\text{ }\rho \text{ }\pi \text{ }{{r}^{3}}}}{{3{{\varepsilon }_{0}}}}
or E = \displaystyle \frac{\rho }{{3{{\varepsilon }_{0}}}}r
i.e. E ∝ r
Thus, inside the sphere of uniform charge, the field is directly proportional to the distance r from the centre. The variation of E with distance r is shown in the figure.
Illustration
Determine and draw the graph of electric field due to infinitely large non conducting sheet of thickness t and uniform volume charge density σ as a function of distance x from its symmetry plane for .
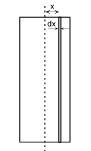
(a) \displaystyle x\le \frac{t}{2}
(b) \displaystyle x\ge \frac{t}{2}
Solution
We can assume thick sheet to be made of large number of uniformly charged thin sheets. Consider an elementary thin sheet of width dx at a distance x from symmetry plane.
Charge in sheet = ρAdx
(A : assumed area of sheet)
surface charge density
\sigma =\frac{{\rho Adx}}{A}
so, electric field intensity due to elementary sheet. dE=\frac{{\rho dx}}{{2{{\varepsilon }_{0}}}}
(a)
When x < t/2
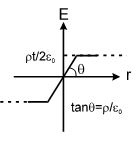
{{E}_{{net}}}=\int\limits_{{-t/2}}^{x}{{\frac{{\rho dx}}{{2{{\varepsilon }_{0}}}}}}-\int\limits_{x}^{{t/2}}{{\frac{{\rho dx}}{{2{{\varepsilon }_{0}}}}}}=\frac{{\rho x}}{{{{\varepsilon }_{0}}}}
(b)
When x > t/2
{{E}_{{net}}}=\int\limits_{{-t/2}}^{{t/2}}{{\frac{{\rho dx}}{{2{{\varepsilon }_{0}}}}}}=\frac{{\rho t}}{{2{{\varepsilon }_{0}}}}
Illustration
Two conducting plates of large surface area M and N are placed parallel to each other. M is given a charge \displaystyle {{Q}_{1}} and N is given a charge \displaystyle {{Q}_{2}}. Find the distribution of charges on the four surfaces.
Solution
Consider the closed Gaussian surface as indicated by the dashed line. The flux through two faces which lie inside the plates is zero because there is no electric field inside the conductors. The flux through other four surface is zero because electric field lines do not pass through there surfaces.
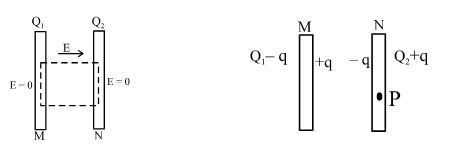
Therefore, the electric flux through the closed surface is zero. From gauss’s law, the total charge enclosed should be zero. Hence, the charge on two opposite faces should be equal and opposite. The distribution is shown in the other figure.
To find q, we consider a point P inside plate N. Let the area of the plates be A.
Using formula E=\frac{\sigma }{{2{{\varepsilon }_{o}}}}
the electric field at P due to
charge Q1-q = \frac{{{{Q}_{1}}-q}}{{2A{{\varepsilon }_{0}}}} ( rightward)
charge + q = \frac{q}{{2A{{\varepsilon }_{0}}}} ( rightward)
charge – q = \frac{q}{{2A{{\varepsilon }_{0}}}} ( leftward)
charge Q2+q = \frac{{{{Q}_{2}}+q}}{{2A{{\varepsilon }_{0}}}} ( leftward)
E=\frac{{{{Q}_{1}}-q}}{{2A{{\varepsilon }_{0}}}}+\frac{q}{{2A{{\varepsilon }_{0}}}}-\frac{q}{{2A{{\varepsilon }_{0}}}}-\frac{{{{Q}_{2}}+q}}{{2A{{\varepsilon }_{0}}}}
Since point P is inside the conductor, this field should be zero.
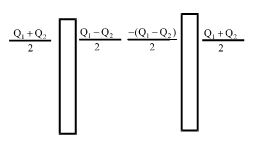
Therefore Q1-q = Q2+q or q=\frac{{{{Q}_{1}}+{{Q}_{2}}}}{2}
Therefore the charge distribution is as shown in the figure below.
Some important Cases
(3)
If a closed body (not enclosing any charge) is placed in an electric field (either uniform or non-uniform) total flux linked with it will be zero
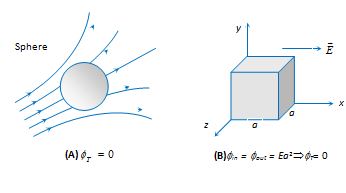
(4)
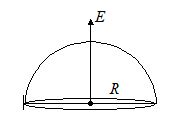
If a hemispherical body is placed in uniform electric field then flux linked with the curved surface calculated as follows
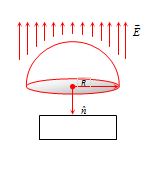
{{\varphi }_{{Curved}}}+{{\varphi }_{{Circular}}}=0
{{\varphi }_{{Curved}}}=-{{\varphi }_{{Circular}}}
=-\,(E\times \pi {{R}^{2}}\cos 180{}^\circ )
=+\pi {{R}^{2}}E
(5)
If a hemispherical body is placed in non-uniform electric field as shown below. then flux linked with the circular surface calculated as follows
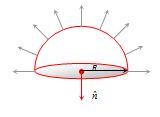
{{\varphi }_{{Circular}}}=-{{\varphi }_{{Curved}}}
{{\varphi }_{{Circular}}}=-\,(E\times 2\pi {{R}^{2}}\cos 0{}^\circ )
=-\,2\pi {{R}^{2}}E
(6)
If charge is kept at the centre of cube
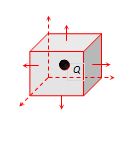
{{\varphi }_{{total}}}=\frac{1}{{{{\varepsilon }_{0}}}}.(Q)
{{\varphi }_{{face}}}=\frac{Q}{{6{{\varepsilon }_{0}}}}
{{\varphi }_{{corner}}}=\frac{Q}{{8{{\varepsilon }_{0}}}}
{{\varphi }_{{edge}}}=\frac{Q}{{12{{\varepsilon }_{0}}}}
(7)
If charge is kept at the centre of a face : First we should enclosed the charge by assuming a Gaussian surface (an identical imaginary cube)
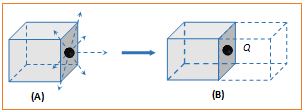
Total flux emerges from the system (Two cubes) {{\varphi }_{{total}}}=\frac{Q}{{{{\varepsilon }_{0}}}}
Flux from given cube (i.e. from 5 face only) {{\varphi }_{{cube}}}=\frac{Q}{{2{{\varepsilon }_{0}}}}
(8)
If a charge is kept at the corner of a cube
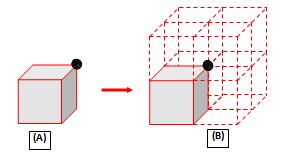
For enclosing the charge seven more cubes are required so total flux from the 8 cube system is fT = \frac{Q}{{{{\varepsilon }_{0}}}} .
Flux from given cube {{\varphi }_{{cube}}}=\frac{Q}{{8{{\varepsilon }_{0}}}} .
Flux from one face opposite to change, of the given cube {{\varphi }_{{face}}}=\frac{{Q/8{{\varepsilon }_{0}}}}{3}=\frac{Q}{{24{{\varepsilon }_{0}}}} (Because only three faces are seen).
(9)
A long straight wire of charge density λ penetrates a hollow body as shown. The flux emerges from the body is
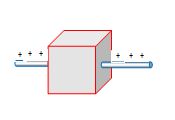
φ = λx (Length of the wire inside the body)
Practice Questions (Basic Level)
Q.1
A charge Q is located at the centre of a cube. The electric flux through any face of the cube is
(a) Q/12 eo
(b) 4p Q/eo
(c) Q/6 eo
(d) Q/4 peo
Ans. (c)
Q.2
How many electrons must be added to a spherical conductor of radius 10 cm to produce a field of 2 ´ 10–3 N/C just above the surface
(a) 1.39 ´ 104
(b) 1.6 ´ 105
(c) 3 ´ 104
(d) 9.1 ´ 104
Ans. (a)
Q.3
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The total flux for the surface of the cylinder is given by
(a) 2pR2E
(b) 2pR2/E
(c) zero
(d) none of these
Ans. (c)
Q.4
A hemispherical surface of radius R is placed with its cross-section perpendicular to a uniform electric field E as shown in figure. Flux linked with its curved surface is
(a) zero
(b) 2\pi {{R}^{2}}E
(c) pR2E
(d) \frac{E}{{2{{\varepsilon }_{o}}}}
Ans. (c)
Q.5
A hollow conducting sphere of charge does not produce an electric field at any
(1) Interior point
(2) Outer point
(3) Point beyond 2 metre
(4) Point beyond 10 metre
Ans. (1)
Q.6
A positive point charge, which is free to move, is placed inside a hollow conducting sphere, placed away from it centre. The conducting sphere is uniformly charged with negative charge. The positive charge will
(1) Move towards the centre
(2) Move towards the nearer wall of the conductor
(3) Remain stationary
(4) Oscillate between the centre and the nearer wall
Ans. (3)
Q.7
How does the electric field strength vary when we enter a uniformly charged spherical cloud ?
(1) Decreases inversely as the square of the distance from the surface.
(2) Decreases directly as the square of the distance from the surface
(3) Increase directly as the square of the distance from the centre
(4) Increases directly as the distance from the centre.
Ans. (4)
Q.8
Gauss’s law helps in
(1) Determination of electric force between point charges
(2) Situations where Coulomb’s law fails
(3) Determination of electric field due to symmetric charge distributions
(4) Determining electric potential due to symmetric charge distributions.
Ans. (3)
Q.9
Which one of the following graphs, figures shows the variation of electric field strength E with distance d from the centre of the hollow conducting sphere ?
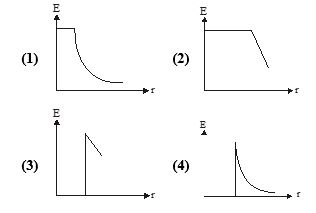
Ans (4)
10.
If an insulated non-conducting sphere of radius R has charge density r. The electric field at a distance r from the centre of sphere (r<R) will be
(a) \frac{{\rho R}}{{3{{\varepsilon }_{0}}}}
(b) \frac{{\rho r}}{{{{\varepsilon }_{0}}}}
(c) \frac{{\rho r}}{{3{{\varepsilon }_{0}}}}
(d) \frac{{3\rho R}}{{{{\varepsilon }_{0}}}}
Ans (c)
11.
Shown in the figure is a distribution of charges. The flux of electric field due to these charges through the surface is
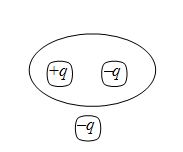
(a) 3 q / e0
(b) 2 q / e0
(c) q / e0
(d) Zero
Ans (d)
12.
The inward and outward electric flux for a closed surface in units of N-m2/coulomb are respectively 8 × 103 and 4 × 103. Then the total charge inside the surface is
(a) 4 × 103 coulomb
(b) – 4 × 103 coulomb
(c) -\frac{{4\times {{{10}}^{3}}}}{{{{\varepsilon }_{0}}}}coulomb
(d) – (4 × 103 )e0 coulomb
Ans (d)
Practice Questions (JEE Main Level)
Q.1
Which of the following statements are correct?
(a) Electric field calculated by Gauss law is the field due to only those charges which are enclosed inside the Gaussian surface.
(b) Gauss law is applicable only when there is a symmetrical distribution of charge.
(c) Electric flux through a closed surface will depends only on charges enclosed within that surface only.
(d) None of these
Ans. (c)
Q.2
A charged body has an electric flux f associated with it. The body is now placed inside a metallic container. The electric flux f1 outside the container will be
(a) f1 = 0 (b) 0 < f1 < f (c) f1 = f (d) f1 > f
Ans. (c)
Q.3
Two large parallel planes charged uniformly with surface charge density s and –s are located as shown in the figure. Which one of the following graphs shows the variation of electric field along a line perpendicular to the planes as one moves from A to B?
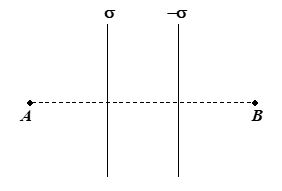
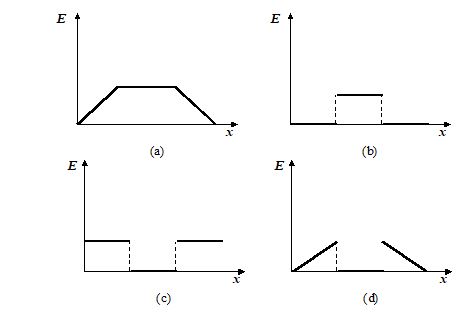
Ans. (b)
Q.4
Due to a charge inside the cube, the electric field is: Ex = 600×1/2, Ey = 0, Ez = 0. The charge inside the cube is nearly
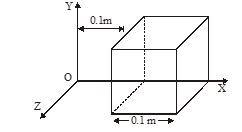
(a) 600µC
(b) 60µC
(c) 7µµC
(d) 6µµC
Ans. (c)
Q.5
An isolated solid metal sphere of radius R is given an electric charge. Which one of the following best represents the way in which the density of charge varies with distance r from the centre of the sphere?
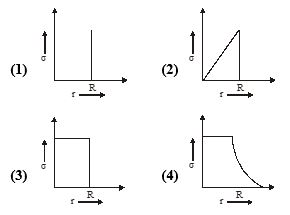
Ans. (a)
Q.6
A charge q is distributed uniformly on a ring of radius r. A sphere of equal radius r is constructed with its centre at the perihery of the ring (figure). The electric flux through the surface of the sphere is
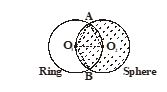
(a) \displaystyle \frac{q}{{{{\varepsilon }_{0}}}}
(b) \displaystyle \frac{{2q}}{{{{\varepsilon }_{0}}}}
(c) \displaystyle \frac{q}{{2{{\varepsilon }_{0}}}}
(d) \displaystyle \frac{q}{{3{{\varepsilon }_{0}}}}
Ans. (d)
Q.7
A cylinder of radius r and length l is placed in an uniform electric field in such a way that the axis of the cylinder is parallel to the field. The flux of the field through the cylindrical surface is
(a) \displaystyle \frac{{100Q}}{{\pi {{\varepsilon }_{0}}}}
(b) \displaystyle \frac{l}{{{{\varepsilon }_{0}}}}
(c) \displaystyle \frac{{2\pi rl}}{{{{\varepsilon }_{0}}}}
(d) zero
Ans : (d)
Q.8
Charge is distributed non-uniformly in the volume of a solid insulating sphere of radius ‘a’ such that volume charge density (ρ) varies with distance from the centre (r) as \displaystyle \rho (r)=C{{r}^{2}},\,\,r\le a here C is a constant. Magnitude of electric field strength outside the sphere, i.e., for is :
(a) \displaystyle \frac{{C{{a}^{5}}}}{{5{{\varepsilon }_{0}}{{r}^{2}}}}
(b) \displaystyle \frac{{C{{r}^{3}}}}{{5{{\varepsilon }_{0}}}}
(c) \displaystyle \frac{{C{{r}^{2}}}}{{2{{\varepsilon }_{0}}}}
(d) \displaystyle \frac{{C{{a}^{3}}}}{{{{\varepsilon }_{0}}{{r}^{2}}}}
Q.9
A charge is placed at the centre of a cube with side L. The electric flux linked with cubical surface is :
(a) \displaystyle (Q/6{{L}^{2}}{{\varepsilon }_{0}})
(b) \displaystyle (Q/{{L}^{2}}{{\varepsilon }_{0}})
(c) \displaystyle (Q/{{\varepsilon }_{0}})
(d) zero
Ans : (c)
Q.10
A charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is :
(a) \displaystyle (Q/{{\varepsilon }_{0}})
(b) \displaystyle (Q/2{{\varepsilon }_{0}})
(c) \displaystyle (Q/4{{\varepsilon }_{0}})
(d) \displaystyle (Q/6{{\varepsilon }_{0}})
Ans : (d)
Q.11
A cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
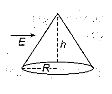
(a) \displaystyle E\pi {{R}^{2}}
(b) \displaystyle \frac{{EhR}}{2}
(c) \displaystyle \frac{{EhR}}{2}
(d) \displaystyle E{{h}^{2}}
Ans : (b)
Q.12
A point charge +Q is positioned at the centre of the base of a square pyramid as shown. The flux through one of the four identical upper faces of the pyramid is
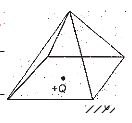
(a) \displaystyle \frac{Q}{{16{{\varepsilon }_{0}}}}
(b) \displaystyle \frac{Q}{{4{{\varepsilon }_{0}}}}
(c) \displaystyle \frac{Q}{{8{{\varepsilon }_{0}}}}
(d) None of these
Ans: (c)
Q.13
Electric charge is uniformly distributed along a along straight wire of radius 1mm. The charge per centimeter length of the wire is Q coulomb. Another Cylindrical surface of radius 50 cm and length 1 m symmetrically encloses the wire ask shown in figure. The total electric flux passing through the cylindrical surface is
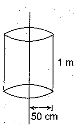
(a) \displaystyle \frac{Q}{{{{\varepsilon }_{0}}}}
(b) \displaystyle \frac{{100Q}}{{{{\varepsilon }_{0}}}}
(c) \displaystyle \frac{{10Q}}{{\pi {{\varepsilon }_{0}}}}
(d) \displaystyle \frac{{100Q}}{{\pi {{\varepsilon }_{0}}}}
Ans : (b)
Q.14
A spherical portion has been removed from a solid sphere having a charge distributed uniformly in its volume as shown in the Fig. The electric field inside the emptied space is :

(a) zero everywhere
(b) non-zero and uniform
(c) none-uniform
(d) zero only at its centre
Ans : (b)
Q.15
Two concentric conducting thin spherical shells A and B having radii \displaystyle {{r}_{A}} and \displaystyle {{r}_{B}}({{r}_{B}}>{{r}_{A}})are charged to QA and –QB \displaystyle (|{{Q}_{B}}|>{{Q}_{A}}|). The electric field along a line (passing through the centre) is :

Ans. (a)
Practice Questions (JEE Advance Level)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
