Video Lecture
Theory For Making Notes
Electric Field
Electric Field is the space around a charge in which its influence (electric forces) can be experienced. In principle the electric field of a charge extends upto infinity.
In other words an electric charge influences its surroundings by creating an electric field. The second charge does not interact directly with the first, rather, it responds to whatever field it encounters.
Electric Field Intensity
The electric field strength or intensity due to a point source charge q at any point P at a distance r from it is given by the force acting on a unit positive test charge placed at that point.
The electric field strength \vec{E} at a point is defined as the force \vec{F} per unit charge experienced by a vanishing small positive test charge q0
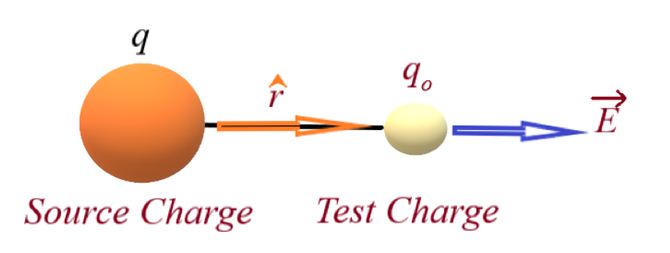
\displaystyle \vec{E}=\underset{{{{q}_{0}}\to 0}}{\mathop{{\lim }}}\,\frac{F}{{{{q}_{0}}}}
\vec{E} is also called the electric field intensity or simply the electric field.
Note that \vec{E} at a point is equal to the force experienced by a unit positive charge placed at that point. Obviously, if \vec{E} is the electric field at any point, then the force experienced by a charge q at that point is
\vec{F}= q \vec{E}
SI unit of \displaystyle \vec{E} is Newton per coulomb (N/C), which is same as volt per metre (V/m):
unit of E\text{ }=\text{ }\frac{\text{N}}{\text{C}}\text{ }=\text{ }\frac{\text{J}}{\text{m}}\text{ }\times \text{ }\frac{\text{1}}{\text{C}}\text{ }=\text{ }\frac{\text{J}}{\text{C}}\text{ }\times \text{ }\frac{\text{1}}{\text{m}}\text{ }=\text{ }\frac{\text{V}}{\text{m}}
The dimensions of E are [MLT–3A–1].
The electric field created by a point charge q is given by
\displaystyle \vec{E} = \displaystyle \frac{{kq}}{{{{r}^{2}}}}\hat{r}
where the unit vector r has it origin at the source charge q as shown in the figure
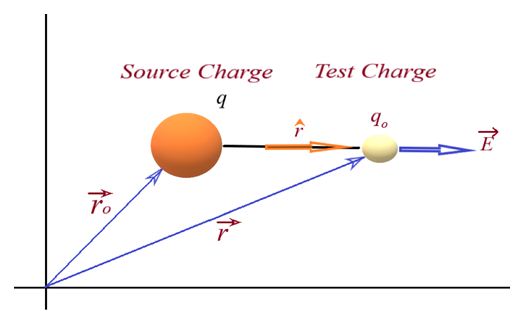
Vector form of electric field at position vector \displaystyle \vec{r} due to a point charge q placed at a point whose position vector is \displaystyle {{\vec{r}}_{0}} is given as \displaystyle \vec{E}=\frac{{kq\left( {\vec{r}-{{{\vec{r}}}_{0}}} \right)}}{{|\vec{r}-{{{\vec{r}}}_{0}}{{|}^{3}}}}
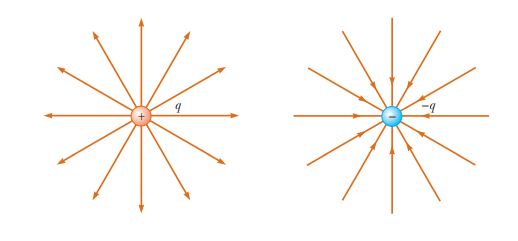
The electric field due to a charge points away from the charge if it is positive and towards it if the charge is negative as shown in the diagram given below
Principle of superposition
Since the principle of superposition is valid for Coulomb’s law, it is also valid for the electric field. To calculate the field strength at point due to a system of charges, we first find the individual field intensity {{\vec{E}}_{1}} due to q1, {{\vec{E}}_{2}} due to q2 and so on.
For N point charges, the resultant field intensity is the vector sum of all the individual electric fields due to different charges, so if \vec{E} is the net electric field then it is given by
\vec{E} = {{\vec{E}}_{1}} + {{\vec{E}}_{2}} + …….. + {{\vec{E}}_{N}}
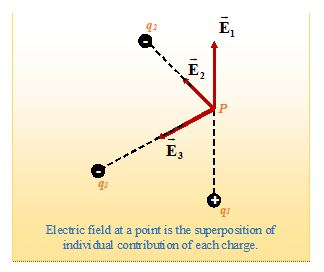
Let the point charges \displaystyle {{q}_{1}},\,\,{{q}_{2}},\,\,{{q}_{3}},\,\,…… placed at the points whose position vectors are \displaystyle {{\vec{r}}_{1}},\,\,{{\vec{r}}_{2}},\,\,{{\vec{r}}_{3}},\,\,……. respectively. Then their net electric field at a point whose position vector \displaystyle \vec{r} is given as
\displaystyle \vec{E}\,\,=\,\frac{{k{{q}_{1}}\,\left( {\vec{r}-{{{\vec{r}}}_{1}}} \right)}}{{|\vec{r}-{{{\vec{r}}}_{1}}{{|}^{3}}}}\,+\,\frac{{k{{q}_{2}}\,\left( {\vec{r}-{{{\vec{r}}}_{2}}} \right)}}{{|\vec{r}-{{{\vec{r}}}_{2}}{{|}^{3}}}}\,+\,\frac{{k{{q}_{3}}\,\left( {\vec{r}-{{{\vec{r}}}_{3}}} \right)}}{{|\vec{r}-{{{\vec{r}}}_{3}}{{|}^{3}}}}+\,……..=k\sum\limits_{{i=1}}^{{i=N}}{{\frac{{k{{q}_{i}}\,\left( {\vec{r}-{{{\vec{r}}}_{i}}} \right)}}{{|\vec{r}-{{{\vec{r}}}_{i}}{{|}^{3}}}}}}
This is also known as superposition principle.
Motion of a charged particle in an electric field
Let a particle of mass m, charge q be situated in an electric field of strength E, then force on the charged particle is given by \overset{\to }{\mathop{F}}\,=q.\overset{\to }{\mathop{E}}\,
The acceleration a produced by this force is \overset{\to }{\mathop{a}}\,=\frac{{\overset{\to }{\mathop{F}}\,}}{m}=\frac{{q\overset{\to }{\mathop{E}}\,}}{m} …(i)
If the particle is at rest at t = 0, then velocity of charged particle after time t is
\vec{v}=\vec{u}+\vec{a}t=0+\frac{{q\vec{E}}}{m}t
or \vec{v}=\frac{{q\vec{E}}}{m}t …(ii)
and distance traversed by the particle is \vec{s}=\vec{u}t+\frac{1}{2}\left( {\frac{{q\vec{E}}}{m}} \right){{t}^{2}}
or \vec{s}=\frac{1}{2}\left( {\frac{{q\vec{E}}}{m}} \right){{t}^{2}} …(iii)
and kinetic energy K =\frac{1}{2}m\left( {\frac{{qE}}{m}{{t}^{2}}} \right) =\frac{1}{2}m\frac{{{{q}^{2}}{{E}^{2}}}}{{{{m}^{2}}}}{{t}^{2}}
K=\frac{{{{q}^{2}}{{E}^{2}}}}{{2m}}{{t}^{2}} …(iv)
If a charged particle enter in field in perpendicular direction, then force on the particle is along Y-axis is given by {{\overset{\to }{\mathop{F}}\,}_{Y}}=q.\overset{\to }{\mathop{E}}\,
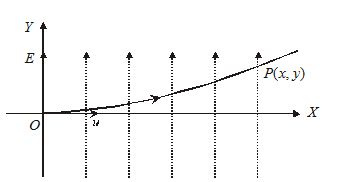
Acceleration of the particle along Y–axis {{\overset{\to }{\mathop{a}}\,}_{Y}}=\frac{{{{{\overset{\to }{\mathop{F}}\,}}_{Y}}}}{m}
Initial velocity is u along x – axis and it is zero along Y–axis. The deflection after time t along y-axis is
y=\frac{1}{2}\frac{{qE}}{m}{{t}^{2}} …(v)
As there is no acceleration along X-axis, therefore the distance traversed by particle in time t along X–axis
x=ut …(vi)
From (v) and (vi), we get
y=\frac{1}{2}.\frac{{qE}}{m}{{\left( {\frac{x}{u}} \right)}^{2}} \Rightarrow y\propto {{x}^{2}}
This shows that the path of the charged particle in perpendicular field is a parabola.
Electric field due to a uniformly charged ring on its axis.
Let a total positive charge Q is distributed uniformly around a thin, circular, non-conducting ring of radius a. Let us calculate its electric field E at a point P along the axis of the ring, at a distance x from the centre, as shown in figure.
Consider a element charge dq on the ring and its electric field is written at the point P
As \displaystyle \vec{E}=\frac{{kdq}}{{{{r}^{2}}}}\hat{r} , where the magnitude \displaystyle dE = \frac{{k dq}}{{({{a}^{2}}+{{x}^{2}})}} . We can find its two components one along the x axis i.e. dEx the other perpendicular to x axis i.e. dE⊥
Note the symmetry. Every element dq can be paired with a similar element on the opposite side of the ring. Every component dE⊥ perpendicular to the x-axis is thus cancelled by an equal component dE⊥ in the opposite direction. In the summation process, all the perpendicular components dE⊥ add to zero. Thus, we are to add only the dE⊥ components.
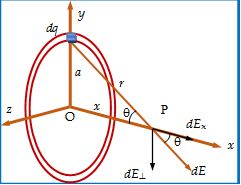
Its x-component is
\displaystyle d{{E}_{\text{x}}} = dE \text{cos} \theta = \frac{{k dq}}{{({{a}^{2}}+{{x}^{2}})}}.\frac{x}{{\sqrt{{{{a}^{2}}+{{x}^{2}}}}}}
E = Ex = \displaystyle \int{{d{{E}_{x}}}} = k\int{{\frac{{x dq}}{{{{{({{a}^{2}}+{{x}^{2}})}}^{{3/2}}}}}}}
As we integrate around the ring,
\displaystyle \int{{dq}}=Q
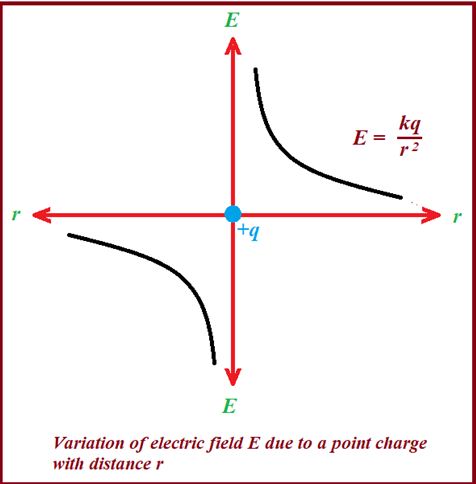
\displaystyle E = \frac{{k x Q}}{{{{{({{a}^{2}}+{{x}^{2}})}}^{{3/2}}}}}
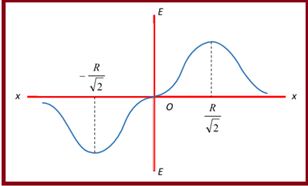
Note that At centre x = 0 so Ecentre = 0
Whereas at a point on the axis such that x>>a. On neglecting a from the denominator we get E=\frac{{kQ}}{{{{x}^{2}}}}
If we differentiate E with respect to x and putting dE/dx equal to zero we get x=\pm \frac{R}{{\sqrt{2}}}, It is the point where the electric field becomes maximum with magnitude {{E}_{{\max }}}=\frac{Q}{{6\sqrt{3}\pi {{\varepsilon }_{0}}{{a}^{2}}}}
Graph showing the variation of electric field of a ring with distance x
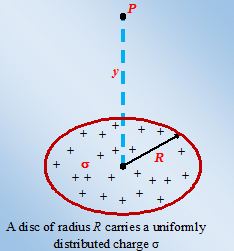
Electric field due to charged Disc On its Axis
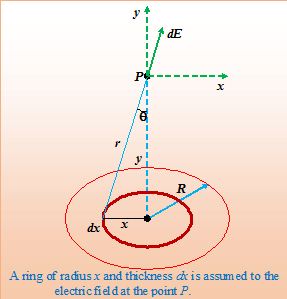
Let us calculate the field intensity at a distance y from the centre along the central axis of a circular disc of radius R and surface charge density σ(C/m2).
Due to circular symmetry of the disc, a ring of radius x and width dx is chosen. All points of the ring are equidistant from the point P.
Consider a component of the field parallel to the plane of the disc. Any contribution of this component from some point on the ring has an equal and opposite contribution from the diametrically opposite part of the ring.
Thus, due to symmetry, there is no component of the field parallel to the plane of the disc
i.e. Ex= 0
The y-component of the field is
dEy = dE cos θ = \frac{{kdq}}{{{{r}^{2}}}}\,\frac{y}{r}
where dq = σdA = σ(2pxdx)
and r2 = x2 + y2
dEy= \frac{{k\sigma \left( {2\pi xdx} \right)y}}{{{{{({{x}^{2}}\,+{{y}^{2}})}}^{{3/2}}}}}
On integrating
Ey= πkσy \int\limits_{0}^{R}{{\frac{{2x\,\,dx}}{{{{{({{x}^{2}}\,+{{y}^{2}})}}^{{3/2}}}}}}}
or Ey= 2πkσ \left[ {1\,-\,\frac{y}{{{{{({{R}^{2}}\,+\,{{y}^{2}})}}^{{1/2}}}}}} \right] (i)
Note
When y >>R, using binomial theorem.
\frac{y}{{{{{({{y}^{2}}\,+\,{{R}^{2}})}}^{{1/2}}}}}\,=\,{{\left( {1\,+\,\frac{{{{R}^{2}}}}{{{{y}^{2}}}}} \right)}^{{-1/2}}}\,\approx \,\,1\,-\frac{{{{R}^{2}}}}{{2{{y}^{2}}}}
Thus, the expression reduces to
Ey= \frac{{\pi k\sigma {{R}^{2}}}}{{{{y}^{2}}}}
or Ey= \frac{{kq}}{{{{y}^{2}}}} since q = s(pR2)
Which represents the electric field due to a point charge
As R →∞, the disc behaves like an infinite sheet and the expression (i) reduces to
E = 2πkσ = σ/2εo
Illustration
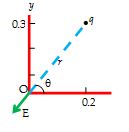
A 5.0µC point charge is placed at the point x = 0.2 cm, y = 0.3 cm. Find the magnitude of \displaystyle \overrightarrow{E} due to it (a) at the origin and (b) at point A with coordinates x = 1.0m, y = 1.0 m.
Solution
(a) The direction of \displaystyle \overrightarrow{E} at the origin is shown in figure
The distance of point O from the charge is
\displaystyle r=\sqrt{{{{{(0.2)}}^{2}}+{{{(0.3)}}^{2}}}}=0.36\text{m}
also \displaystyle \tan \theta =\frac{{0.3}}{{0.2}}=1.5 Þ q = tan–1 1.5 = 56.3°
The magnitude of electric intensity is
\displaystyle E=\frac{{kq}}{{{{r}^{2}}}}=\frac{{(9\times {{{10}}^{9}})\,\,(5\times {{{10}}^{{-6}}})}}{{{{{(0.36)}}^{2}}}}=3.46\times {{10}^{5}}\text{N}{{\text{C}}^{{-1}}}
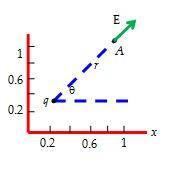
(b) The distance between the charge q and the point A is
\displaystyle r=\sqrt{{{{{(1.0-0.2)}}^{2}}+{{{(1.0-0.3)}}^{2}}}}=1.06\text{m}
\displaystyle \tan \theta =\frac{{0.7}}{{0.8}}=\frac{7}{8}
\displaystyle \theta ={{\tan }^{{-1}}}\frac{7}{8}=41.2{}^\circ
The magnitude of E is
\displaystyle E=\frac{{kq}}{{{{r}^{2}}}}=\frac{{(9\times {{{10}}^{9}})\,(5\times {{{10}}^{{-6}}})}}{{{{{(1.06)}}^{2}}}}=4\times {{10}^{4}}\text{N}
Illustration
The figure shows a system of two charges. A point charge \displaystyle {{q}_{1}} = 20nC is at (-1,0) while \displaystyle {{q}_{2}} = -10nC is at (+1,0). Find the resultant field intensity at a point P with coordinates (2,2).
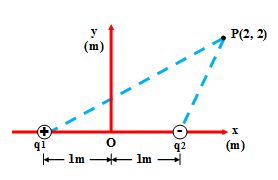
Solution
1.
The field vector \displaystyle {{E}_{1}} points away from the charge \displaystyle {{q}_{1}} while the vector \displaystyle {{E}_{2}} points toward the charge \displaystyle {{q}_{2}}.
2.
The distance \displaystyle {{r}_{1}} and \displaystyle {{r}_{2}} are
\displaystyle {{r}_{1}} = \sqrt{{{{{(2+1)}}^{2}}\,+{{2}^{2}}}}\,=\sqrt{{13}}=3.6\,m
\displaystyle {{r}_{2}} = \sqrt{{{{1}^{2}}\,+{{2}^{2}}}}\,=\sqrt{5}\,=\,2.2\,m
The magnitude of the fields are
\displaystyle {{E}_{1}} = \frac{{k{{q}_{1}}}}{{r_{1}^{2}}}\,\,=\,\,\frac{{\left( {9\,\,\times \,{{{10}}^{9}}} \right)\,\,\left( {20\,\,\times \,{{{10}}^{{-9}}}} \right)}}{{{{{(3.6)}}^{2}}}} =\,13.8\,N{{C}^{{-1}}}
\displaystyle {{E}_{2}} = \displaystyle \frac{{k{{q}_{2}}}}{{r_{2}^{2}}}\,\,=\,\,\frac{{\left( {9\,\,\times \,{{{10}}^{9}}} \right)\,\,\left( {10\,\,\times \,{{{10}}^{{-9}}}} \right)}}{{{{{(2.2)}}^{2}}}} \displaystyle =\,18\,\,N{{C}^{{-1}}}
3.
The components of the resultant field are
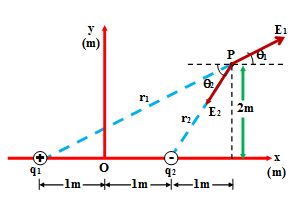
\displaystyle {{E}_{x}}={{E}_{1}}\cos {{\theta }_{1}}-{{E}_{2}}\cos {{\theta }_{2}}
\displaystyle {{E}_{y}}={{E}_{1}}\cos {{\theta }_{1}}-{{E}_{2}}\cos {{\theta }_{2}}
were \displaystyle \cos {{\theta }_{1}} = \frac{3}{{3.6}} ; \displaystyle \cos {{\theta }_{2}}= \frac{1}{{2.2}}
and \displaystyle \sin {{\theta }_{1}} = \frac{2}{{3.6}} ; \displaystyle \sin {{\theta }_{2}} = \frac{2}{{2.2}}
Thus, Ex = (13.8) \frac{3}{{3.6}}\,-\,18\,\left( {\frac{1}{{2.2}}} \right)\,=\,3.3\,N/C
Ey = (13.8) \frac{2}{{3.6}} – 18 \left( {\frac{2}{{2.2}}} \right) = -8.7 NC–1
Finally, \displaystyle \overrightarrow{E}=3.3\hat{i}-8.7\hat{j}\,N{{C}^{{-1}}}
Illustration
Three point charges are placed at the corners of an equilateral triangle as shown in figure. What is the value of electric field at the centre.
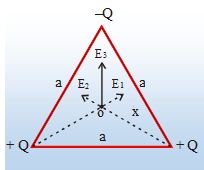
Solution
Let us take origin at the centre and x and y-axis as shown in figure.
E1, E2 and E3 are the electric field due to +Q, +Q and – Q.
\displaystyle {{\vec{E}}_{1}}=\frac{Q}{{4\pi {{\in }_{0}}{{{\left( {\frac{a}{{\sqrt{3}}}} \right)}}^{2}}}}(\cos 30{}^\circ \hat{i}+\sin 30{}^\circ \hat{j})
\displaystyle {{\vec{E}}_{2}}=\frac{Q}{{4\pi {{\in }_{0}}{{{\left( {\frac{a}{{\sqrt{3}}}} \right)}}^{2}}}}(-\cos 30{}^\circ \hat{i}+\sin 30{}^\circ \hat{j})
\displaystyle {{\vec{E}}_{3}}=\frac{Q}{{4\pi {{\in }_{0}}{{{\left( {\frac{a}{{\sqrt{3}}}} \right)}}^{2}}}}(+\hat{j})
\displaystyle {{\vec{E}}_{{net}}}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}+{{\vec{E}}_{3}}
\displaystyle =\frac{{6Q}}{{4\pi {{\in }_{0}}{{a}^{2}}}}\hat{j}
Illustration
Find the field intensity at a point P at a distance R from a finite line of charge of length L and linear charge density l C/m, as shown in the Fig. (A).
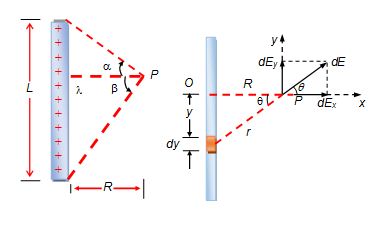
Solution
Consider a small element of length dy at a distance y, as shown in Fig. (B). The magnitude of the contribution to the field at point P due to this element is
\displaystyle dE=\frac{{k\text{ }\lambda dy}}{{{{r}^{2}}}} …(i)
To carry out the integration we express the variables in terms of the angle q. From the figure,
r = R sec q and y = R tan q
on differentiating, dy = R sec2q. Thus, Eqn. (i) becomes
\displaystyle dE=\frac{{k\text{ }\lambda (Rse{{c}^{2}}\theta \text{ }d\theta )}}{{{{{(R \sec \theta )}}^{2}}}} = \frac{{k\text{ }\lambda d\theta }}{R}
The components of dE along x-axis and y-axis are
dEx = dE cos q; dEy = dE sin q
On integrating, we get
\displaystyle {{E}_{\text{x}}} = \frac{{k\text{ }\lambda }}{R} \int\limits_{{-\beta }}^{{+\alpha }}{{}}\cos \text{ }\theta d\theta = \frac{{k\text{ }\lambda }}{R}\text{ }\left. {\left( {\sin \text{ }\theta } \right)} \right|_{{-\beta }}^{{+\alpha }} = \displaystyle \frac{{k\text{ }\lambda }}{R}\text{ }\left( {\sin \text{ }\alpha \text{ }+\text{ }\sin \text{ }\beta } \right)
and \displaystyle {{E}_{\text{y}}} = \frac{{k\text{ }\lambda }}{R} \int\limits_{{-\beta }}^{{+\alpha }}{{}}\sin \text{ }\theta d\theta = \frac{{k\text{ }\lambda }}{R}\text{ }\left. {\left( {-\cos \text{ }\theta } \right)} \right|_{{-\beta }}^{{+\alpha }} = \displaystyle \frac{{k\lambda }}{R}\text{ }\left( {\text{cos }\beta \text{ }-\text{ cos }\alpha } \right)
The magnitude of the net field at point P will be
\displaystyle E=\sqrt{{E_{x}^{2}+E_{y}^{2}}}
Important Points
(i)
If the point P is at the perpendicular bisector of the line charge then a = b
andEx = \displaystyle \frac{{k\text{ }\lambda }}{R} 2 sin a = \displaystyle \frac{{k\text{ }\lambda }}{R} \displaystyle \frac{L}{{\sqrt{{{{{\left( {{}^{L}\!\!\diagup\!\!{}_{2}\;} \right)}}^{2}}+{{R}^{2}}}}}}
Ey = 0
(ii)
If the charge were distributed over an infinite length the both a and b approaches π/2.
Illustration
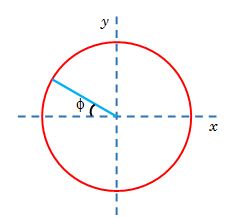
A thin conducting ring of radius R is charged with a linear density \lambda ={{\lambda }_{0}}\cos \varphi , where {{\lambda }_{0}} is a positive constant and \varphi is the angle shown in fig. Find the electric field intensity E at the center of the ring.
Solution
Consider a differential element of charge dq whose field at center O.
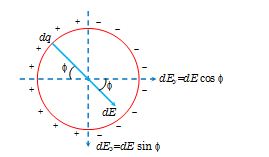
the components of its field are d{{E}_{x}}=dE\cos \varphi =\frac{{kdq}}{{{{R}^{2}}}}\cos \varphi =\frac{{k\lambda R\varphi }}{{{{R}^{2}}}}\cos \varphi
{{E}_{x}}=\int{{d{{E}_{x}}=\frac{k}{R}{{\lambda }_{0}}\int\limits_{0}^{{2\pi }}{{{{{\cos }}^{2}}\varphi }}\,\,d\,\,\varphi }}
=\frac{{k{{\lambda }_{0}}}}{{2R}}\int\limits_{0}^{{2\pi }}{{\left( {1-\cos 2\varphi } \right)d\varphi }}
or {{E}_{x}}=\frac{{k{{\lambda }_{0}}}}{{2R}}\left[ {\int\limits_{0}^{{2\pi }}{{d\varphi -\int\limits_{0}^{{2\pi }}{{\cos 2\varphi d\varphi }}}}} \right]
=\frac{{k{{\lambda }_{0}}}}{{2R}}2\pi =\frac{{k{{\lambda }_{0}}\pi }}{R}=\frac{{{{\lambda }_{0}}}}{{4{{\varepsilon }_{0}}R}}
Similarly,
{{E}_{y}}=\int\limits_{0}^{{2\pi }}{{\frac{{k{{\lambda }_{0}}}}{{2R}}\sin \varphi \cos \varphi \,d\varphi }}
or {{E}_{y}}=\frac{{k{{\lambda }_{0}}}}{{2R}}\int\limits_{0}^{{2\pi }}{{\sin 2\varphi d\varphi =\frac{{k{{\lambda }_{0}}}}{{4R}}\left[ {-\cos 2\varphi } \right]_{0}^{{2\pi }}=0}}
Hence the net field at O is along the x-axis and its magnitude is \frac{{{{\lambda }_{0}}}}{{4{{\varepsilon }_{0}}R}}. The symmetry of this distribution also implies that the field is directed along x-axis.
Practice Questions (Basic Level)
Q.1
Figure shows a charge +Q a distance 2d from a charge –Q and a point X distance d from –Q. The field strength at X is numerically, using SI units
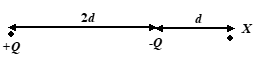
(a) \frac{Q}{{4\pi {{\varepsilon }_{o}}{{d}^{2}}}}
(b) \frac{Q}{{36\pi {{\varepsilon }_{o}}{{d}^{2}}}}
(c) \frac{{3Q}}{{4\pi {{\varepsilon }_{o}}{{d}^{2}}}}
(d) \frac{{2Q}}{{9\pi {{\varepsilon }_{o}}{{d}^{2}}}}
Ans .(d)
Q.2
A positively charged pendulum is oscillating in a uniform electric field as shown in the figure. Its time period as compared to that when it was uncharged
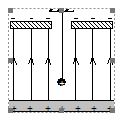
(a) will increase
(b) will decrease
(c) will not change
(d) will first increase then decrease
Ans. (a)
Q.3
A drop of oil density r and radius r carries a charge q when placed in a electric field E, its moves upwards with a velocity n.
If r0 is the density of air, h be the viscosity of the air, then which of the following forces is directed upwards ?
(a) 6 p h r n
(b) q E
(c) \frac{4}{3}\pi {{r}^{3}}(\rho -{{\rho }_{0}})g
(d) qE + 6 p r h n
Ans. (b)
Q.4
The diagram shows electric lines of force. If EA and EB are electric fields at A and B and distance AB = r, then
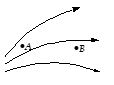
(a) EA > EB
(b) EA = EB/r
(c) EA < EB
(d EA = EB/r
Ans (a)
Q.5
Charges 2Q and –Q are placed as shown. The point at which electric field intensity is zero will be
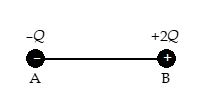
(a) somewhere between –Q and 2Q
(b) somewhere on the left of –Q
(c) somewhere on the right of 2Q
(d) somewhere on the right bisector of line joining –Q and 2Q
Ans. (b)
Q.6
Five point charges (+q each) are placed at the five vertices of a regular hexagon of side 2a. What is the magnitude of the net electric field at the centre of the hexagon?
(a) \frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{q}{{{{a}^{2}}}}
(b) \frac{q}{{16\pi {{\varepsilon }_{o}}{{a}^{2}}}}
(c) \frac{{\sqrt{2}\,q}}{{4\pi {{\varepsilon }_{o}}{{a}^{2}}}}
(d) \frac{{5q}}{{16\pi {{\varepsilon }_{o}}{{a}^{2}}}}
Ans . (b)
Q. 7
In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges of magnitude Q are placed at (n-1) corners. The field at the centre is
(a) k \frac{Q}{{r2}}
(b) (n-1)k \frac{Q}{{r2}}
(c) \frac{n}{{n-1}}k \frac{Q}{{r2}}
(d) \frac{{n-1}}{n}k \displaystyle \frac{Q}{{r2}}
Ans . (a)
Q.8
Charge Q is given a displacement =aî+bĵ in an electric field =E1î+E2ĵ. The work done is
(a) Q(E1a+E2b)
(b) Q \sqrt{{(E1a)2+(E2b)2}}
(c) Q(E1+E2) \sqrt{{a2+b2}}
(d) Q \displaystyle \sqrt{{(E12+(E22}}
Ans .(a)
Q.9
Which of the following is not true for a region with a uniform electric field?
(a) It can have free charges
(b) It may have uniformly distributed charge.
(c) It may contain dipoles.
(d) None of the above.
Ans. (d)
Q.10
A simple pendulum of time period T is suspended above a large horizontal metal sheet with uniformly distributed positive charge. If the bob is given some negative charge, its time period of oscillation will be
(a) >T
(b) <T
(c) T
(d) proportional to its amplitude.
Ans. (b)
Q. 11
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be :
(a) \displaystyle \frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\frac{q}{{3\sqrt{3}{{R}^{2}}}}
(b) \displaystyle \frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\frac{{2q}}{{3{{R}^{2}}}}
(c) \displaystyle \frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\frac{{2q}}{{3\sqrt{3}{{R}^{2}}}}
(d) \displaystyle \frac{1}{{4\pi {{\varepsilon }_{0}}}}\,\,\frac{{3q}}{{2\sqrt{2}{{R}^{2}}}}
Ans. (c)
Q.12
Two particles A and B (B is right of A) having charges and , respectively, are held fixed with separation of 20 cm. Where should a third charged particle be placed so that it does not experience a net electric force.
(a) 5cm right of B
(b) 5cm left of A
(c) 20cm left of A
(d) 20cm right of B
Ans. (d)
Q.13
Two particles of masses in the ratio 1 : 2, with charges in the ratio 1 : 1, are placed at rest in a uniform electric field. They are released and allowed to move for the same time. The ratio of their kinetic energies will be finally
(a) 2 : 1
(b) 8 : 1
(c) 4 : 1
(d) 1 : 4
Ans. (a)
Q.14
An electron of mass , initially at rest, moves through a certain distance in a uniform electric field in time . A proton of mass also initially at rest, takes time to move through an equal distance in this uniform electric field. Neglecting the effect of gravity, the ratio is nearly equal to
(a) 1
(b) \displaystyle \sqrt{{{{M}_{p}}/{{M}_{e}}}}
(c) \displaystyle \sqrt{{{{M}_{e}}/{{M}_{p}}}}
(d) 1836
Ans. (b)
15.
Two point charges +8q and -2q are located at x = 0 and x = L respectively. The location of a point on the x-axis at which the net electric field due to these two point charges is zero, is
(a) 2 L
(b) \frac{L}{4}
(c) 8 L
(d) 4 L
Ans (a)
Practice Questions (JEE Main Level)
Q.1
The intensity of electric field due to a ring of radius R at a distance x from its centre on the axis of ring carrying charge Q is given by
E = \frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{{Qx}}{{{{{\left( {{{R}^{2}}+{{x}^{2}}} \right)}}^{{3/2}}}}}
The distance from the centre of the ring where intensity of electric field will be maximum is
(a) x = R
(b) x = R/2
(c) x = \sqrt{2}R
(d) x = \frac{R}{{\sqrt{2}}}
Ans. (d)
Q.2
A spring-block system undergoes vertical oscillation above a large horizontal metal sheet with uniform positive charge. The time period of the oscillation is T. If the block is given a charge Q, its time period of oscillation will be
(a) T (b) >T (c) T if Q is positive and
Ans. (a)
Q.3
A large flat metal surface has a uniform charge density +s. An electron of mass m and charge e leaves the surface at point A with speed u, and returns to it at point B. Disregard gravity. The maximum value of AB is
(a) \frac{{u2m\varepsilon 0}}{{\sigma e}}
(b) \frac{{u2e\varepsilon 0}}{{m\sigma }}
(c) \frac{{u2e}}{{\varepsilon 0\sigma m}}
(d) \frac{{u2\sigma e}}{{\varepsilon 0m}}
Ans. (a)
Q.4
An extremely long wire is uniformly charged. An electron is revolving about the wire and making 108 revolutions per second in an orbit of radius 2cm. Linear charge density of the wire is nearly :
(a) 50 nC (b) 25 nC (c) 62.5 nC (d) 12.5 nC
Ans. (a)
Q.5
Four identical charges Q are fixed at the four corners of a square of side a. The electric field at a point P located symmetrically at a distance from the center of the square is
(a) \displaystyle \frac{Q}{{2\sqrt{2}\pi {{\varepsilon }_{0}}{{a}^{2}}}}
(b) \displaystyle \frac{Q}{{\sqrt{2}\pi {{\varepsilon }_{0}}{{a}^{2}}}}
(c) \displaystyle \frac{{2\sqrt{2}Q}}{{\pi {{\varepsilon }_{0}}{{a}^{2}}}}
(d) \displaystyle \frac{{\sqrt{2}Q}}{{\pi {{\varepsilon }_{0}}{{a}^{2}}}}
Ans. (b)
Q.6
One of the two parallel metallic plates is uniformly charged with charge +q and the other one is charged with charge –q. In this case, the electric field between them is E. When the negatively charged plate is discharged then recharged with a positive charge 4q, the magnitude of electric field between the plates becomes
(a) 1.5 E (b) 2.5 E (c) 3 E (d) 5 E
Ans..(a)
Q.7
Consider three identical metal spheres A, B and C. Spheres A carries charge + 6q and sphere B carries charge – 3 Sphere C carries no charge. Spheres A and B are touched together and then separated. Sphere C is then touched to sphere A and separated from it. Finally the sphere C is touched to sphere B and separated from it. Find the final charge on the sphere C.
Ans. \displaystyle \frac{{9Q}}{8}
Q.8
Two positive point charges of magnitude Q each are separated by a distance “2a”. A test charge is located in a plane which is normal to the line joining these charges and midway between them. The locus of the points in this plane for which the force on the test charge has a maximum value is
(a) a circle of radius r=a/\sqrt{2}
(b) a circle of radius r=a
(c) a straight line
(d) an ellipse
Ans. (a)
Q.9
A particle of mass m and charge q is placed at rest in a uniform electric field E as shown and released. The kinetic energy it attains after moving a distance y is
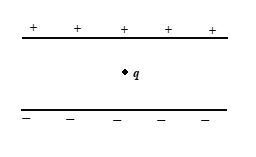
(a) \frac{1}{2}qEy
(b) qEy
(c) qE2y
(d) \frac{1}{2}m(qEy)
Ans. (b)
Q.10
The electric field on two sides of a charged plate is shown in the figure. The charge density on the plate is given by
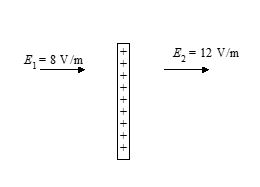
(a) 2eo
(b) 4eo
(c) 10eo
(d) zero
Ans. (b)
Q.11
A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge –Q is uniformly distributed along the lower half. The electric field E at P, the center of the semicircle, is
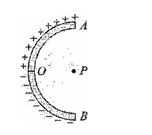
(a) \displaystyle \frac{Q}{{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}}}
(b) \displaystyle \frac{{2Q}}{{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}}}
(c) \displaystyle \frac{{4Q}}{{{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}}}
(d) \displaystyle \frac{Q}{{4{{\pi }^{2}}{{\varepsilon }_{0}}{{r}^{2}}}}
Ans. (a)
Q.12
A block of mass m having charge q, is hinged by a spring of spring constant k in a vertical electrostatic field E. The spring extension in equilibrium will be
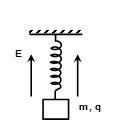
(A)\displaystyle\frac{{mg}}{k}
(B) \displaystyle \frac{{qE}}{k}
(C) \displaystyle \frac{{mg+qE}}{k}
(D) \displaystyle \frac{{mg-qE}}{k}
Q. 13
Two identical point charges are placed at a separation of l. P is a point on the line joining the charges, at a distance x from any one charge. The field at P is E. E is plotted against x for values of x from close to zero to slightly less than l. Which of the following best represents the resulting curve?
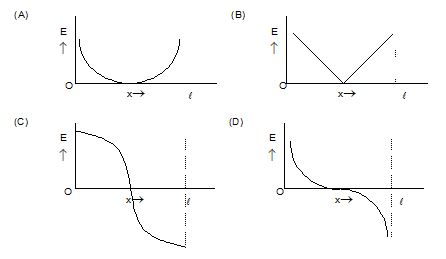
Ans. (d)
Q.14
Figure shows a uniformly charged hemispherical shell. The direction of electric field at point p, that is off-centre (but in the plane of the largest circle of the hemisphere), will be along
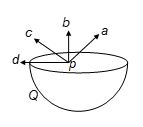
(a) pa
(b) pb
(c) pc
(d) pd
Ans. (b)
Q.15
Three charges + 2Q, – 3Q and –Q are arranged in a line as shown in the figure. The number of points along the line at which the net electric field is zero is
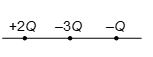
(a) 1
(b) 2
(c) 3
(d) More than 3
Ans. (b)
Practice Questions (JEE Advance Level)
Q.1
A particle of mass m and charge –q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement.
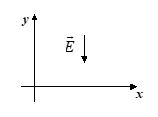
(a) The kinetic energy after a displacement y is qEy.
(b) The horizontal and vertical components of acceleration are ax = 0, ay = \frac{{qE}}{m}
(c) The equation of trajectory is y = \frac{1}{2}\left( {\frac{{qE{{x}^{2}}}}{{m{{v}^{2}}}}} \right)
(d) The horizontal and vertical displacements x and y after a time t are x = vt and
y = \frac{1}{2}{{a}_{y}}{{t}^{2}}
Ans. (a)
Q.2
A small ball of mass m and charge +q tied with a string of length l, is rotating in a vertical circle under gravity and a uniform horizontal electric field E as shown. The tension in the string will be minimum for
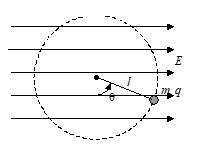
(a) \theta ={{\tan }^{{-1}}}\left( {\frac{{qE}}{{mg}}} \right)
(b) q = p
(c) q = p – {{\tan }^{{-1}}}\left( {\frac{{qE}}{{mg}}} \right)
(d) q = p + {{\tan }^{{-1}}}\left( {\frac{{qE}}{{mg}}} \right)
Ans. (d)
Q.3
The variation of electric field between the two charges q1 and q2 along the line joining the charges is plotted against distance from q1 (taking rightward direction of electric field as positive) as shown in the figure. Then the correct statement is
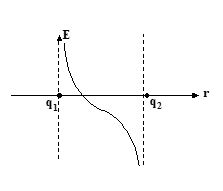
(a) q1 and q2 are positive and q1 < q2
(b) q1 and q2 are positive and q1 > q2
(c) q1 is positive and q2 is negative and q1 < q2
(d) q1 and q2 are negative and q1 < q2
Ans. (a)
Q.4
Consider a regular cube with positive point charge + Q in all corners except for one which has a negative point charge – Q. Let the distance from any corner to the center of the cube be r. The magnitude of electric field at point P, the center of the cube will be
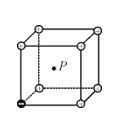
(a) E = 7keQ/r2
(b) E = 1keQ/r2
(c) E = 2keQ/r2
(d) E = 6keQ/r2
Ans. (d)
Q.5
The figure shows, two point charges q1 = 2Q ( > 0) and
q2 = –Q. The charges divide the line joining them in three parts I, II and III.
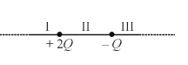
(a) Region III has a local maxima of electric field.
(b) Region I has a local minima of electric field.
(c) Equilibrium position for a test charge lies in region II.
(d) The equilibrium for constrained motion along the line joining the charges is stable for a positive test charge.
Ans. (a)
Q.6
A simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density \sigma =\frac{{2mg{{\in }_{0}}}}{q} . If suddenly a charge +q is given to the bob and it is released from the position shown in figure. The maximum angle through which the string is deflected from vertical will be
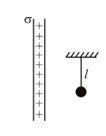
(a) 90°
(b) 60°
(c) 45°
(d) 30°
Ans. (a)
Q.7
A particle of mass m and negative charge q is thrown in a gravity free space with speed u from the point A on the large non conducting charged sheet with surface charge density s, as shown in figure. The maximum distance from A on sheet where the particle can strike will be
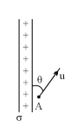
(a) \frac{{m{{u}^{2}}{{\varepsilon }_{0}}}}{{q\sigma }}
(b) \frac{{\sqrt{2}\ m{{u}^{2}}{{\varepsilon }_{0}}}}{{q\sigma }}
(c) \displaystyle \frac{{2m{{u}^{2}}{{\varepsilon }_{0}}}}{{q\sigma }}
(d) \frac{{m{{u}^{2}}{{\varepsilon }_{0}}}}{{2q\sigma }}
Ans. (c)
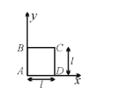
Q.8
A square loop of side ‘l‘ each side having uniform linear charge density ‘l’ is placed in ‘xy’ plane as shown in the figure. There exists a non-uniform electric field \vec{E}=\frac{a}{l}(x+l)\,\hat{i} where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons), if l = 10 cm, l = 20 mC/m and a = 5 × 105 N/C.
(a) 9N
(b) 6N
(c) 45N
(d) 30N
Ans. (b)
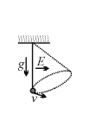
Q. 9
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists. The particle is drawn aside so that the string becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
(a) 9N
(b) 6N
(c) 45N
(d) 30N
Ans. (b)
Q. 9
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists. The particle is drawn aside so that the string becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

(a) \frac{{e\lambda }}{{\pi {{\varepsilon }_{0}}\,mR}}\,\,\left( {\frac{{3\,-\,2\sqrt{2}}}{{4\,\sqrt{6}}}} \right)
(b) \frac{{e\lambda }}{{\pi {{\varepsilon }_{0}}\,mR}}\,\,\left( {\frac{{3\,+\,2\sqrt{2}}}{{4\,\sqrt{6}}}} \right)
(c) \frac{{e\lambda }}{{\pi {{\varepsilon }_{0}}\,mR}}\,\,\left( {\frac{{3\,+\,2\sqrt{2}}}{{4\,\sqrt{3}}}} \right)
(d) None of these
Ans. (a)
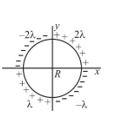
Q.11
The charge per unit length of the four quadrant of the ring is 2l, – 2l, l and – l respectively. The electric field at the centre is
(a) \frac{\lambda }{{2\pi {{\varepsilon }_{0}}R}}\ \hat{i}
(b) \frac{\lambda }{{2\pi {{\varepsilon }_{0}}R}}\ \hat{j}
(c) \frac{{\sqrt{2}\ \lambda }}{{4\pi {{\varepsilon }_{0}}R}}\ \hat{i}
(d) None of these
Ans. (b)
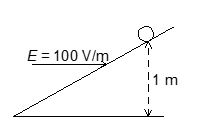
Q.12
An inclined plane making an angle of 30° with the horizontal is placed in a uniform electric field E of 100 V/m (see figure). A particle of mass 1 kg and charge 0.01 C is allowed to slide down from rest from a height of 1 m. If the coefficient of friction is 0.2, the time taken by the particle to reach the bottom will be
(a) 1.2 sec
(b) 1.337 sec
(c) 1.447 sec
(d) 1.5 sec
Ans. (a)
Q.13
A particle of mass m and charge Q is placed in an electric field E which varies with time t as . It will undergo simple harmonic motion of amplitude.
(a) \frac{{QE_{0}^{2}}}{{m{{\omega }^{2}}}}
(b) \frac{{Q{{E}_{0}}}}{{m{{\omega }^{2}}}}
(c) \sqrt{{\frac{{Q{{E}_{0}}}}{{m\omega }}}}
(d) \frac{{Q{{E}_{0}}}}{{m\omega }}
Ans. (b)
Q.14
A nonconducting ring of radius R has uniformly distributed positive charge Q. A small part of the ring, of length d, is removed (d << R). The electric field at the centre of the ring will now be
(a) directed towards the gap, inversely proportional to R3.
(b) directed towards the gap, inversely proportional to R2.
(c) directed away from the gap, inversely proportional to R3.
(d) directed away from the gap, inversely proportional to R2.
Ans. (a)
Q.15
Electric field in a space is given as E={{E}_{0}}x(x-1)(x-2)(x-3) N/C along X. axis. Where E0 is a positive constant.
(a) Electric field is along positive direction at x=\frac{1}{2}
(b) Electric field is along negative direction at x=\frac{3}{2}
(c) A positive charge is in stable equilibrium at x=2
(d) A negative charge is in stable equilibrium at x=2
Ans. (c)
Q.16
Two infinitely long charged wires with linear densities l and 3l are placed along x and y axis respectively determined the slope of electric field and any point on the line y=\sqrt{{3x}}.
Ans. 30°
Q.17
Three charges + 2Q, – 3Q and –Q are arranged in a line as shown in the figure. The number of points along the line at which the net electric field is zero is
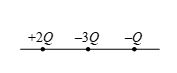
(a) 1 (b) 2 (c) 3 (d) More than 3
Ans. (b)
18.
Two semi-infinite line charges with linear density + \displaystyle \lambda C/m and – \displaystyle \lambda C/m lie along the x-axis with their ends located at x = –a and x = +a, as shown in fig. What is the electric field strength at the origin ?
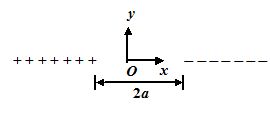
(a) \frac{{2k\lambda }}{a}
(b) \frac{{k\lambda }}{a}
(c) \frac{{9k\lambda }}{a}
(d) \frac{{5k\lambda }}{a}
Ans (a)
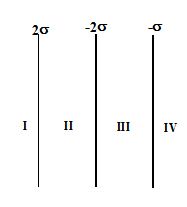
19.
Three infinite parallel charged sheets are placed as shown .The electric field on the four regions indicated in the figure in respective order must be
(a) \displaystyle {{E}_{I}}=\frac{\sigma }{{5{{\varepsilon }_{o}}}},{{E}_{{II}}}=\frac{{5\sigma }}{{2{{\varepsilon }_{o}}}},{{E}_{{III}}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{IV}}}=-\frac{\sigma }{{5{{\varepsilon }_{o}}}}
(b) \displaystyle {{E}_{I}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{II}}}=\frac{{2\sigma }}{{2{{\varepsilon }_{o}}}},{{E}_{{III}}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{IV}}}=-\frac{\sigma }{{2{{\varepsilon }_{o}}}}
(c) \displaystyle {{E}_{I}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{II}}}=\frac{{5\sigma }}{{2{{\varepsilon }_{o}}}},{{E}_{{III}}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{IV}}}=-\frac{\sigma }{{2{{\varepsilon }_{o}}}}
(d) \displaystyle {{E}_{I}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{II}}}=\frac{{5\sigma }}{{2{{\varepsilon }_{o}}}},{{E}_{{III}}}=\frac{\sigma }{{2{{\varepsilon }_{o}}}},{{E}_{{IV}}}=-\frac{\sigma }{{2{{\varepsilon }_{o}}}}
Ans : (d)
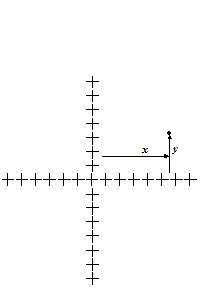
20.
Two infinite lines of charge with equal linear charge densities \displaystyle \lambda C/m are placed along the x and y axes, as in figure. What is the electric field strength at an arbitrary point (x, y) ?
(a) \frac{\lambda }{{2\pi {{\varepsilon }_{o}}}} \left( {\frac{1}{x}\hat{i}\,+\frac{1}{y}\,\hat{j}} \right)
(b) \frac{\lambda }{{pi {{\varepsilon }_{o}}}} \left( {\frac{1}{x}\hat{i}\,+\frac{1}{y}\,\hat{j}} \right)
(c) \frac{\lambda }{{1\pi {{\varepsilon }_{o}}}} \left( {\frac{1}{x}\hat{i}\,+\frac{1}{y}\,\hat{j}} \right)
(d) \frac{\lambda }{{8\pi {{\varepsilon }_{o}}}} \left( {\frac{1}{x}\hat{i}\,+\frac{1}{y}\,\hat{j}} \right)
Ans (a)
Comprehension Question (21 To 23)
An electron is accelerated from rest by a uniform field of magnitude 105 N/C
(21)
How long does it take to reach 0.1c, where c = 3 ´ 10 8 m/s is the speed of light ?
(i) 1.5 ns
(ii) 1.3 ns
(iii) 1.7 ns
(iv)1.2 ns
Ans (iii)
(22)
How far does it travel in this time?
(i) 2.00 cm
(ii) 1.5 cm
(iii) 2.56 cm
(iv) 3.5 cm
Ans (iii)
(23)
What is the final kinetic energy?
Neglect relativistic effects.
(i) 4.1 ´ 10–16 J
(ii) 3.5 ´ 10–16 J
(iii) 2 ´ 10–16 J
(iv) 7 ´ 10–16 J
Ans (i)
24.
Point charge q and -q are located at the vertices of a square with diagonals 2l as shown in figure. Find the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of the square at a distance x from its center.
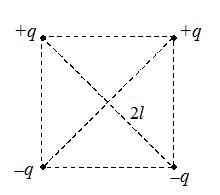
(a) \frac{{ql}}{{\sqrt{2}\,\pi {{\varepsilon }_{o}}{{{\left( {{{l}^{2}}+{{x}^{2}}} \right)}}^{{1/2}}}}}
(b) \frac{{ql}}{{\sqrt{3}\,\pi {{\varepsilon }_{o}}{{{\left( {{{l}^{2}}+{{x}^{2}}} \right)}}^{{4/6}}}}}
(c) \frac{{ql}}{{\sqrt{2}\,\pi {{\varepsilon }_{o}}{{{\left( {{{l}^{5}}+{{x}^{2}}} \right)}}^{{1/5}}}}}
(d) \frac{{ql}}{{\sqrt{2}\,\pi {{\varepsilon }_{o}}{{{\left( {{{l}^{2}}+{{x}^{2}}} \right)}}^{{3/2}}}}}
Ans (d)
25.
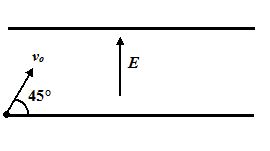
An electron is fired with an initial speed vo at 45° to the horizontal from the bottom plate of a parallel plate arrangement as shown. The plates are separated by 2 cm and are very long. What is the maximum value of vofor the electron not to hit the upper plate ? Take E = 103 N/C.
(a) 1.75 ´ 106 m/s
(b) 3.75 ´ 106 m/s
(c) 5.75 ´ 106 m/s
(d) 3.5 ´ 106 m/s
Ans (b)
