Video Lecture
Theory For Making Notes
Pascal’s Law And Its Application In Manometer
Pressure In a Fluid
When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contact with it, such as a container wall or a body immersed in the fluid.
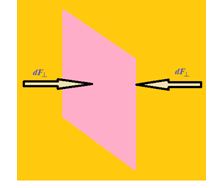
While the fluid as a whole is at rest, the molecules that makes up the fluid are in motion, the force exerted by the fluid is due to molecules colliding with their surrounding.
If we think of an imaginary surface within the fluid, the fluid on the two sides of the surface exerts equal and opposite forces on the surface, otherwise the surface would accelerate and the fluid would not remain at rest.
Consider a small surface of area dA centered on a point on the fluid, the normal force exerted by the fluid on each side is d^. The pressure P is defined at that point as the normal force per unit area, i.e., P=\frac{{d{{F}_{\bot }}}}{{dA}}
If the pressure be the same at all points of a finite plane surface with area A, then P=\frac{{{{F}_{\bot }}}}{A}
Where F^ is the normal force on one side of the surface. The SI unit of pressure in pascal, where
(1 pascal = 1 Pa = 1.0 N/m2)
One unit used principally in meterology is the Bar, which is equal to 105 Pa.
1 Bar = 105 Pa.
Atmospheric Pressure (P0)
It is pressure of the earth’s atmosphere. This changes with weather and elevation. Normal atmospheric pressure at sea level (an average) is 1.013 × 105 Pa. Thus,
1 atm = 1.013 × 105 Pa.
Note:Fluid pressure acts perpendicular to any surface in the fluid no matter how that surface is oriented. Hence, pressure has no intrinsic direction of its own, it’s a scalar. By contrast, force is a vector with a definite direction.
Absolute Pressure And Gauge Pressure
The excess pressure above atmospheric pressure is usually called gauge pressure and the total pressure is called absolute pressure. Thus,
Gauge pressure = absolute pressure – atmospheric pressure
Absolute pressure is always greater than or equal to zero. While gauge pressure can be negative also.
Variation In Pressure With Depth
If the weight of the fluid can be neglected, the pressure in a fluid is the same throughout its volume. But often the fluid’s weight is not negligible and under such condition pressure increases with increasing depth below the surface.
Let us now derive a general relation between the pressure P at any point in a fluid at rest and the elevation y of that point.
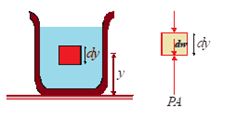
We will assume that the density r and the acceleration due to gravity g are the same throughout the fluid. If the fluid is in equilibrium, every volume element is in equilibrium.
Consider a thin element of fluid with height dy. The bottom and top surfaces each have area A, and they are at elevation y and +yd above some reference level where y = 0. The weight of the fluid element is
dW = (volume) (density) (g) = (A dy) (r) (g)
or dW = rgAdy
What are the other forces in y-direction on this fluid element? Call the pressure at the bottom surface P, the total y component of upward force is PA. The pressure at the top surface is P + dP and the total y-component of downward force on the top surface is (P + dP) A. The fluid element is in equilibrium, so the total y-component of force including the weight and the forces at the bottom and top surfaces must be zero.
´∑Fy = 0
PA – (P + dP)A – rgAdy = 0
or, \frac{{dP}}{{dy}}=-\rho g …(i)
This equation shows that when y increases, P decreases, i.e., as we move upward in the fluid, pressure decreases.
If P1 and P2 be the pressure at elevations y1 and y2 and if r and g are constant, then integration equation (i), we get
\int_{{{{P}_{1}}}}^{{{{P}_{2}}}}{{dP}}=-\rho g\int_{{{{y}_{1}}}}^{{{{y}_{2}}}}{{dy}}
or {{P}_{2}}-{{P}_{1}}=-\rho g({{y}_{2}}-{{y}_{1}}) … (ii)
It’s often convenient to express equation (ii) in terms of the depth below the surface of a fluid. Take point 1 at depth h below the surface of fluid and let P represents pressure at this point. Take point 2 at the surface of the fluid, where the pressure is P0 (subscript zero for zero depth). The depth of point 1 below the surface is, h = y2 – y1
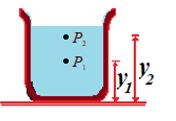
And equation (ii) becomes {{P}_{0}}-P=-\rho g({{y}_{2}}-{{y}_{1}})=-\rho gh
P={{P}_{0}}+\rho gh …(iii)
Thus, pressure increases linearly with depth, if r and g are uniform. A graph between P and h is shown below.
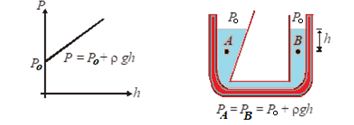
Further, the pressure is the same at any two pints at the same level in the fluid. The shape of the container does not matter.
Illustration
What is the pressure at the bottom of a tank filled with water upto a height of 4 m? Atmospheric pressure is equal to 10 m of water.
Solution:
Pressure at the bottom of the vessel
= atmospheric pressure + pressure due to water column
= 10 m of water + 4 m of water
= 14 m of water
= hrg
= (14 m)(1000 kg/m3)(9.8 m/s2)
= 1.37 x 105 N/m2
Illustration
If the atmospheric pressure is 76 cm of mercury at what depth of water the pressure will be equal to 2 atmosphere?
Density of mercury = 13600 kg/m3.
Solution:
Let the pressure be 2 atm at a depth h below the water surface.
Of this pressure, one atmosphere is due to the atmospheric pressure over the surface of water and hence the pressure due to the water column alone = 1 atm.
= 76 cm of mercury
= (0.76)(13600)(9.8) N/m2
Now a height of h m of water column produces this pressure and we are required to find this height h.
(hrg)water = (hrg)mercury
hx 1000 x 9.8 = 0.76 x 13600 x 9.8
h = \frac{{0.76\,\,\times \,\,13600\,\,\times \,\,9.8}}{{1000\,\,\times \,\,9.8}} = 10.336 m
Hence the height of water barometer corresponding to standard atmospheric pressure is 10.336 m.
Pascal’s Law
It states that “pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel”.
A well known application of Pascal’s law is the hydraulic lift used to support or lift heavy objects. It is schematically illustrated in figure.
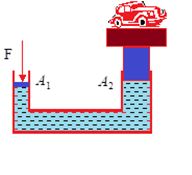
A piston with small cross section area A1 and exerts a force F1 on the surface of a liquid such as oil. The applied pressure P=\frac{{{{F}_{1}}}}{{{{A}_{1}}}}is transmitted through the connecting pipe to a larger piston of area A2. The applied pressure is the same in both cylinders, so
P=\frac{{{{F}_{1}}}}{{{{A}_{1}}}}=\frac{{{{F}_{2}}}}{{{{A}_{2}}}} or {{F}_{2}}=\frac{{{{A}_{2}}}}{{{{A}_{1}}}}.{{F}_{1}}
Now, since A2>A1, therefore, F2>F1. Thus, hydraulic lift is a force multiplying device with a multiplication factor equal to the ratio of the areas of the two pistons. Dentist’s chairs, car lifts and jacks, many elevators and hydraulic brakes all use this principle.
Illustration
Figure shows a hydraulic press with the larger piston of diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10 cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston. The density of oil in the press is 750 kg/m3. Take g = 9.8 m/s2.
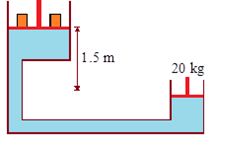
Solution:
Pressure on the smaller piston =\frac{{20\times 9.8}}{{\pi \times {{{(5\times {{{10}}^{{-2}}})}}^{2}}}}\text{N/}{{\text{m}}^{2}}
Pressure on the larger piston =\frac{F}{{\pi \times {{{(5\times {{{10}}^{{-2}}})}}^{2}}}}\text{N/}{{\text{m}}^{2}}
The difference between the two pressures = hrg
Where h = 1.5m and r = 750 kg/m3
Thus, \frac{{20\times 9.8}}{{\pi \times {{{(5\times {{{10}}^{{-2}}})}}^{2}}}}-\frac{F}{{\pi \times {{{(17.5\times {{{10}}^{{-2}}})}}^{2}}}}=1.5\times 750\times 9.8
Which gives, F = 1.3 × 103N
SOME IMPORTANT POINTS
At same point on a fluid pressure is same in all directions.
In the figure, P1 = P2 = P3 = P4
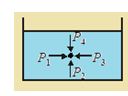
Forces acting on a fluid in equilibrium have to be perpendicular to its surface. Because its cannot sustain the shear stress.
(iii) In the same liquid pressure will be same at all points at the same level.
For example, in the figure:
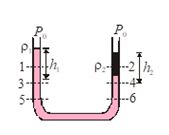
{{P}_{1}}\ne {{P}_{2}}
{{P}_{3}}={{P}_{4}} and {{P}_{5}}={{P}_{6}}
Further, {{P}_{3}}={{P}_{4}}
{{P}_{0}}+{{\rho }_{1}}g{{h}_{1}}={{P}_{0}}+{{\rho }_{2}}g{{h}_{2}}
or {{\rho }_{1}}{{h}_{1}}={{\rho }_{1}}={{\rho }_{2}}{{h}_{2}} or h\propto \frac{1}{\rho }
Barometer:
It is a device used to measure atmospheric pressure.
In principle, any liquid can be used to fill the barometer, but mercury is the substance of choice because its great density makes possible an instrument of reasonable size.
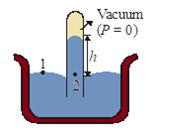
P1 = P2
Here, P1 = atmospheric pressure (P0)
And {{P}_{2}}=0+\rho gh=\rho gh
Here, r = density of mercury
{{P}_{0}}=\rho gh
Thus, the mercury barometer reads the atmospheric pressure (P0)
Directly from the height of the mercury column.
For example if the height of mercury in a barometer is 760 mm, then atmospheric pressure will be,
{{P}_{0}}=\rho gh =(13.6\times {{10}^{3}})(9.8)(0.760) =1.01\times {{10}^{5}}\text{N/}{{\text{m}}^{\text{2}}}
Manometer:
It is a device used to measure the pressure of a gas inside a container.
The U-shaped tube often contains mercury.
P1 = P2
Here, P1 = pressure of the gas in the container (P)
and P2 = atmospheric pressure (P0) + rgh
P={{P}_{0}}+h\rho g
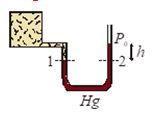
This can also be written as P – P0 = gauge pressure = hrg
(vi)
Free body diagram of a liquid: The free body diagram of the liquid (showing the vertical forces only) is shown in figure (b). For the equilibrium of liquid.
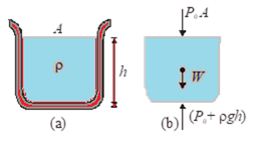
Net downward force = net upward force
{{P}_{0}}A+W=({{P}_{0}}+\rho gh)A
or W = rghA
Illustartion
Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water tat the second vessel requires to fill up to a particular common height. Is the force exerted by water on the base of the vessel the same in the two cases? It so, way do the vessels filled with water to that same height give different readings on a weighing scale?
Solution:
Pressure (and therefore force) on the two equal base areas are identical. But force is exerted by water on the sides of the vessels also, which has a non-zero vertical component when the sides of the vessel are not perfectly normal to the base. This net vertical component of force by water on the sides of the vessel is greater for the first vessel than the second. Hence, the vessels weight different when force on the base is the same in the two cases.
Liquid in accelerated vessel
A Liquid in accelerated vessel can be considered as in the rigid body motion i.e. motion without deformation as though it were a solid body. As in case of static liquid to determine the pressure variation we apply Newton’s law, the same is applicable in case of liquid in accelerated vessel also.
Case I: Variation of pressure and force of buoyancy in a liquid kept in vertically accelerated vessel
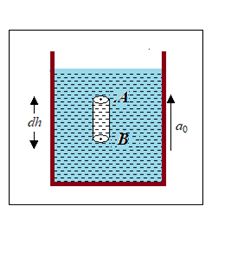
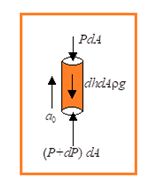
Consider a liquid of density \displaystyle \rho kept in a vessel moving with acceleration a0 in upward direction.
Let A and B are two points separated vertically by a distance dh. The forces acting and vertical liquid column of cross sectional area dA are shown in the figure. For the vertical motion of this liquid column,
(P + dP) dA – PdA – (dh)dA \displaystyle \rho g = (dh)dA \displaystyle \rho a0
dp = \displaystyle \rho (g + a0) dh
If pressure at the free surface of liquid is P0 them pressure P at a depth h from the free surface is given by
\int\limits_{{{{P}_{0}}}}^{P}{{dp=\int\limits_{0}^{h}{{s\left( {g+{{a}_{0}}} \right)}}}}dh
P = P0 + \displaystyle \rho (g + a0) h
On the basis of similar calculation, pressure at any depth h from free surface in case of liquid in downward accelerated vessel can be written of P = P0 + \displaystyle \rho (g– a0) h
We can generalize the above results and conclude that in liquid for a vertically accelerated vessel the pressure at any depth h below the free surface, P = P0 + \displaystyle \rho geffh
Where geff = g + a0 in case of up ward acceleration and geff = g – a0 in case of downward acceleration
Also we can say the force of buoyancy FB on a body in liquid in vertically accelerated vessel is given by FB= V \displaystyle \rho geff
Where V is volume of liquid displaced by the body.
Case II: Shape of free surface of liquid in horizontally accelerated vessel
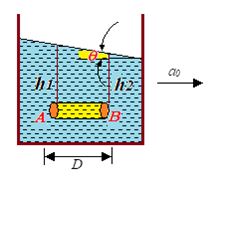
When a vessel filled with liquid accelerates horizontally. We observe its free surface inclined at some angle with horizontal. To find angle \displaystyle \theta made by free surface with horizontal consider a horizontal liquid column including two points, A and B at depths h1 and h2 from the inclined free surface of liquid as shown in figure. D is length of liquid column. Horizontal forces acting on the liquid column are as shown in diagram, for horizontal motion of column we can write,
P1dA – P2dA = \displaystyle \rho (dA) D(a0)
(h1 – h2) g = Pa0
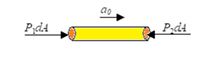
\frac{{{{h}_{1}}-{{h}_{2}}}}{D}=\frac{{{{a}_{0}}}}{g}Þtan \displaystyle \theta = \frac{{{{a}_{0}}}}{g}Þ \theta ={{\tan }^{{-1}}}\frac{{{{a}_{0}}}}{g}
Practice Questions (Basic Level)
Q.1
The vessel shown in the figure has two sections of cross-section A1 and A2. A liquid of density r fills both the sections, up to a height h in each. Neglect atmospheric pressure. Which is the following is incorrect?
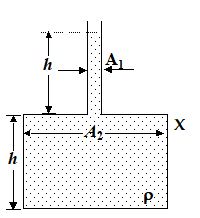
(a) The pressure at the base of the vessel is 2hrg
(b) The force exerted by the liquid on the base of the vessel is 2hrgA2.
(c) The weight of the liquid is 2hrgA2.
(d) The walls of the vessel at the level x exert a downward force hrg(A2 – A1) on the liquid.
Ans. (c)
Q.2
Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. The densities are rA, rB and rC with rA < rB < rC. The force on the base will be
(a) maximum in vessel A
(b) maximum in vessel B
(c) maximum in vessel C
(d) equal in all the vessels
Ans. (d)
Q.3
As a bubble comes from the bottom of a lake to the top, its radius:
(a) Increases (b) Decreases (c) Does not change (d) Becomes zero
Ans. (a)
Q.4
Pressure at a point inside a liquid does not depend on:
(a) The depth of the point below the surface of the liquid
(b) The nature of the liquid
(c) The acceleration due to gravity at that point
(d) The shape of the containing vessel
Ans. (d)
Q.5
Pressure is applied to an enclosed fluid. It is:
(a) Increased and applied to every part of the fluid
(b) Diminished and transmitted to the walls of the container
(c) Increased in proportion to the mass of the fluid and then transmitted
(d) Transmitted unchanged to every portion of the fluid and the walls of container
Ans. (d)
Q.6
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm2. What maximum pressure would smaller piston have to bear?
(a) 6.25 ´ 105 Pa
(b) 2.25 ´ 105 Pa
(c) 4.63 ´ 105 Pa
(d) 6.92 ´ 105 Pa
Ans (d)
Q.7
What force does water exert on the base of a house tank of base area 1.5 m2 when it is filled with water up to a height of 1m? [Density of water is 103 kg/m3 and g = 10 m/s2]
(a) 0.2 ´ 104 N
(b) 5.36 ´ 104 N
(c) 1.5 ´ 104 N
(d) 9.37 ´ 104 N
Ans (c)
Q.8
The three vessels shown in figure have same base area. Equal volumes of a liquid are poured in the three vessels. The force on the base will be
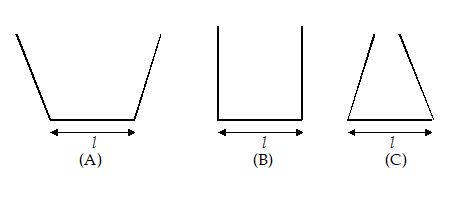
(a) maximum in vessel A
(b) maximum in vessel B
(c) maximum in vessel C
(d) equal in all the vessels
Ans. (c)
Q.9
A vessel contains liquid of density r as shown in figure. The gauge pressure at the point P is:
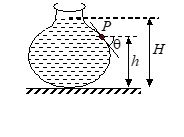
(a) hrg
(b) Hrg
(c) (H – h)rg
(d) (H – h)rg cos q
Ans. (c)
Q.10
The manometer shown in figure, contains oil of density 850 kg/m3. What is the absolute pressure of the gas in the bulb? The atmospheric pressure is
101 kPa.
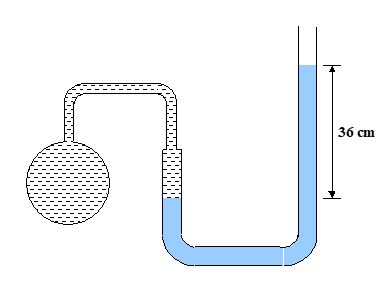
(a) 100 kPa
(b) 104 kPa
(c) 147 kPa
(d) 296 kPa
Ans (b)
Practice Questions (JEE Main Level)
Q.1
The height of water in a vessel is h. The vessel wall of width b is at an angle q to the vertical. The net force exerted by the water on the wall is
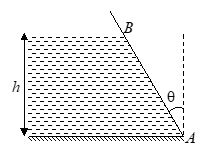
(a) \frac{1}{3}\rho bg{{h}^{2}}g\cos \theta
(b) b{{h}^{2}}\rho g b{{h}^{2}}\rho g
(c) \frac{1}{2}\rho b{{h}^{2}}g\sec \theta
(d) zero
Ans (c)
Q.2
A U shaped tube contains a liquid of density r and it is rotated about the line as shown in the figure. Find the difference in the levels of liquid column.
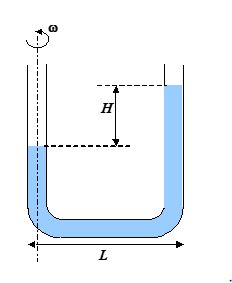
(a) H=\frac{{{{\omega }^{2}}{{L}^{3}}}}{{g}}
(b) H=\frac{{{{\omega }^{2}}{{L}^{5}}}}{{2g}}
(c) H=\frac{{{{\omega }^{2}}{{L}^{2}}}}{{2g}}
(d) H=\frac{{{{\omega }^{2}}{{L}^{3}}}}{{7g}}
Ans (c)
Q.3
Two liquids that do not mix are poured into a U shaped tube as shown in figure. Find the difference in fluid heights in terms of r1, r2 and h.
(a) H = (r1 + r2)h/r2
(b) H = (r1 – r2)h/r2
(c) H = (2r1 – r2)h/r2
(d) H = (r1 – 2r2)h/r2
Ans (b)
Q.4
A dam has a height H and a width b. Assuming that the water level reaches the top, find the net pressure force exerted on the dam. Calculate the magnitude of the force for H = 60 m and b = 200m.
(a) \frac{1}{2}\rho gb{{H}^{2}}; F= 1.453 ´ 109 N
(b) \frac{1}{2}\rho gb{{H}^{2}}; F= 3.528 ´ 109 N
(c) \frac{1}{2}\rho gb{{H}^{3}}; F= 3.528 ´ 109 N
(d) \frac{1}{2}\rho gb{{H}^{-3}}; F= 3.528 ´ 109 N
Ans (b)
Comprehension ( Q.5 to Q.6)
An open U-tube of uniform cross-section contains mercury. When 27.2 cm of water is poured into one limb of the tube, [Relative density of Hg = 13.6]
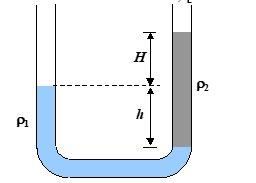
Q.5
how high the mercury rise in the other limb from its initial level?
(a) 1 cm
(b) 5 cm
(c) 15 cm
(d) 50 cm
Ans (a)
Q.6
what is the difference in levels of liquids of the two sides?
(a) 22.2 cm
(b) 20.1 cm
(c) 15.3 cm
(d) 25.2 cm
Ans (d)
Q.7.
Two identical cylindrical vessels with their bases at the same level each contains a liquid of density r. The height of the liquid in one vessel is h1 and that in the other vessel is h2. The area of either base is A. The work done by gravity in equalizing the levels, when the two vessels are connected is:-
(a) (h1 ~ h2)gr
(b) (h1 ~ h2)gAr
(b) (1/2) (h1 ~ h2)2 gAr
(d) (1/4) (h1 ~ h2)2 gAr
Ans. (d)
Practice Questions (JEE Advance Level)
Comprehension ( Q.1 to Q.2)
A cylinder of radius R = 1 m and length H = 3 m, two-third filled with water, is rotated about its vertical axis as shown in figure. Determine the speed of rotation when
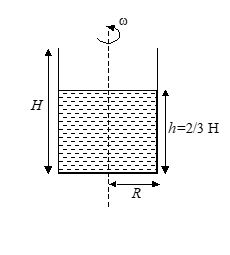
Q.1
The water just starts spilling over the brim
(a) \sqrt{{5}} rad/s
(b) \sqrt{{55}} rad/s
(c) \sqrt{{3}} rad/s
(d) \sqrt{{40}} rad/s
Ans (d)
Q.2
The point at the center of base is just exposed
(a) \sqrt{{55}} rad/s
(b) \sqrt{{60}} rad/s
(c) \sqrt{{44}} rad/s
(d) \sqrt{{5}} rad/s
Ans (b)
Q.3
The interface of two liquids of densities r and 2r respectively lies at the point in a light U tube at rest. The height of liquid column above A is , where AB = a. The cross-sectional area of the tube is S. With what angular velocity it must be whirled about a vertical axis at a distance a such that the interface of the liquids shifts towards B by 2a/3.
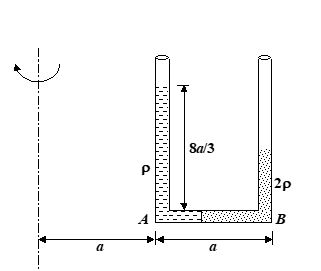
(a) 2\sqrt{{\frac{9}{{20\,\,a}}2g}}
(b) 2\sqrt{{\frac{9}{{20\,\,a}}g}}
(c) 2\sqrt{{\frac{3}{{20\,\,a}}g}}
(d) \sqrt{{\frac{9}{{20\,\,a}}g}}
Ans (d)
Q.4
A liquid stands at the plane level in the U-tube when at rest. If area of cross-section of both the limbs are equal, what will be the difference in heights h of the liquid in the two limbs of U-tube, when the system is given an acceleration a in horizontal direction towards right as shown ?
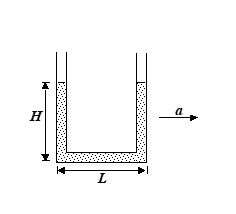
(a) \frac{g}{a}\frac{{{{L}^{2}}}}{H}
(b) \frac{{La}}{g}
(c) \frac{{{{L}^{2}}}}{H}\frac{a}{g}
(d) \frac{{Hg}}{a}
(L = length of horizontal portion of tube, H = initial height of liquid in both limbs)
Ans. (b)
