Video Lecture
Potentiometer
A potentiometer is an instrument which allows the measurement of potential difference without drawing any current from the circuit being measured. Hence, it acts as an infinite-resistance voltmeter.
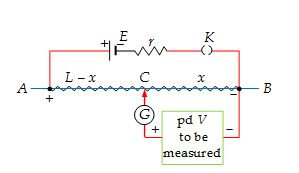
The resistance between A and B is a uniform wire of length L, with a sliding contact C at a distance x and B. The potential difference V is measured by sliding the contact until the galvanometer G reads zero. The no-deflection condition of the galvanometer ensures that there is no current through the branch containing G and the potential difference to be measured. The length x for no-deflection is called as the balancing length.
If l is the resistance per unit length of the wire AB, under balanced condition (i.e., when no current is indicated by galvanometer G), the pd to be measured is given as
\displaystyle V={{V}_{{CB}}}={{V}_{{AB}}}\frac{{{{R}_{{CB}}}}}{{{{R}_{{AB}}}}}={{V}_{{AB}}}\frac{{\lambda \left( x \right)}}{{\lambda L}}
= \left( {\frac{{{{V}_{{\text{AB}}}}}}{L}} \right)\times x
The ratio VAB/L is called the potential gradient in the wire AB.
Comparing Two Cells using Potentiometer
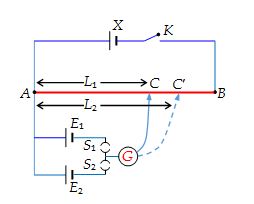
A potentiometer is commonly used for comparison of emfs of cells. A battery X is connected across a long uniform wire AB. The cells E1 and E2 (whose emfs are to be compared) are connected as shown along with a galvanometer.
First the key S1 is pressed which brings E1 in the circuit. The sliding contact C is moved till the galvanometer shows no deflection. Let the length AC = L1. Next S1 is opened and S2 is closed. This brings E2 in the circuit. Let C’ be the new null point and let AC’ = L2. Then, clearly,
\displaystyle \frac{{{{E}_{1}}}}{{{{E}_{2}}}}=\frac{{{{L}_{1}}}}{{{{L}_{2}}}}
Measurement of Internal Resistance of a Cell
A potentiometer can be used to find the internal resistance of a cell. First the emfE of the cell is balanced against a length AC = L. A known resistance R is then connected across the cell as shown. The terminal voltage V is now balanced against a smaller length AC’ = L’.
Then, \displaystyle \frac{E}{V}=\frac{L}{{{L}’}}
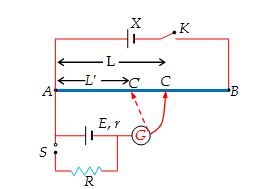
But we know that \displaystyle \frac{E}{V}=\frac{{R+r}}{R}
\displaystyle \frac{{R+r}}{R}=\frac{L}{{{L}’}}
\displaystyle r=\left( {\frac{L}{{{L}’}}-1} \right)R
Illustration
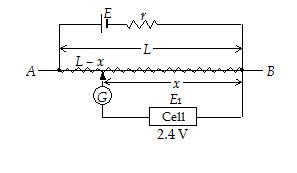
A battery of emf 4 V is connected across a 10 m long potentiometer wire having a resistance per unit length 1.6 W m–1. A cell of emf 2.4 V is connected so that its negative terminal is connected to the low potential end of the potentiometer wire and the other end is connected through a galvanometer to a sliding contact along the wire. It is found that the no-deflection point occurs against the balancing length of 8 m. Calculate the internal resistance of the 4 V battery.
Solution
emf of cell = (potential gradient) X (balancing length)
\displaystyle {{E}_{1}}=\frac{{{{V}_{{AB}}}}}{L}\times x
or \displaystyle 2.4=\frac{{{{V}_{{AB}}}}}{{10}}\times 8
⇒ VAB = 3 V
Consider the loop containing E. Applying potential divider concept,
\displaystyle {{V}_{{AB}}}=E\frac{{{{R}_{{AB}}}}}{{{{R}_{{AB}}}+r}}
⇒ \displaystyle 3=4\frac{{1.6\times 10}}{{1.6\times 10+r}}
⇒ r = 16/3 Ω
Note that as there is no current through the cell and galvanometer, the battery E, the internal resistance r and the potentiometer wire AB are in series.
