Video Lecture
Theory For Notes Making
Potential Due to a Continuous Charge Distribution
The potential due to a continuous charge distribution may be obtained by integration.
First find the potential at the given point (see figure) due to an infinitesimally small point
charge dq.
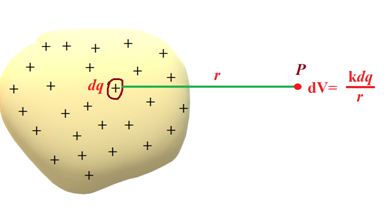
That is dV = \frac{{kdq}}{r}
Now integrate this expression over the whole charge distribution
V = k \int{{\frac{{dq}}{r}}}
Potential due to a uniformly charged ring on its axis
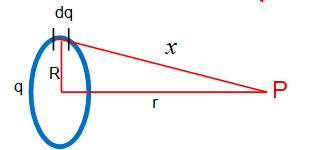
Consider a charge element dq,.Its potential at P is dV where \displaystyle dV=\frac{{kdq}}{x}
Here \displaystyle \text{ }x=\sqrt{{{{R}^{2}}+{{r}^{2}}}} and \displaystyle k=\frac{1}{{4\pi {{\varepsilon }_{o}}}}
\displaystyle \begin{array}{l}\Rightarrow V=-\frac{{KQ}}{R}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}\\\end{array}
Hence dV = \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{{dq}}{{\sqrt{{{{r}^{2}}+{{R}^{2}}}}}} now integrate it to get the total potential V
V = ∫dV = \frac{1}{{4\pi {{\varepsilon }_{0}}\sqrt{{{{r}^{2}}+{{R}^{2}}}}}}∫dq
V = \frac{q}{{4\pi {{\varepsilon }_{0}}\sqrt{{{{r}^{2}}+{{R}^{2}}}}}}
Potential due to a uniformly charged disc
Let the charge on the disc = q, and surface charge density is s = \frac{q}{{\pi {{R}^{2}}}}
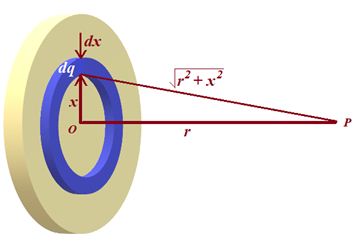
Consider a ring element of radius x and thickness dx. Let the charge on the ring is dq. and the area of the ring is = 2πxdx.
We know that \sigma =\frac{{dq}}{{da}} hence dq=\sigma da=\sigma .2\pi xdx.
Let dV be the potential due to this ring on its axis at point P.
dV=\frac{{kdq}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}}
\displaystyle \Rightarrow dV=\frac{1}{{4\pi {{\varepsilon }_{o}}}}\frac{{\sigma (2\pi xdx)}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}} on integrating we get total potential due to whole disc
\displaystyle \Rightarrow V=\int{{dV=\frac{\sigma }{{2{{\in }_{o}}}}\int\limits_{0}^{R}{{\frac{{xdx}}{{\sqrt{{{{r}^{2}}+{{x}^{2}}}}}}}}}}
Now using the method of substitution to solve this integration we get final answer as
\displaystyle V=\frac{\sigma }{{2{{\in }_{o}}}}[\sqrt{{{{R}^{2}}+{{r}^{2}}}}-r]
Potential due to a uniformly charged spherical shell
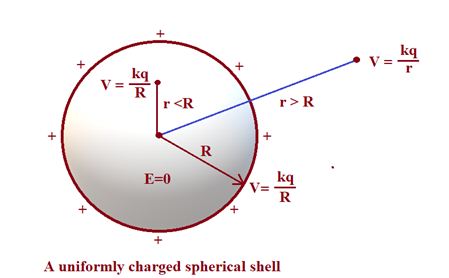
Let the charge on the shell is q. We know that outside the shell
i.e. For r > R, \displaystyle E=\frac{{kq}}{{{{r}^{2}}}}
Also since E = – \frac{{dV}}{{dr}}
Therefore \displaystyle \Rightarrow dV=-E\times dr
On integration from \displaystyle \infty to r, we get \displaystyle \text{ }\int\limits_{\infty }^{r}{{dV}}\text{= -}\int\limits_{\infty }^{\text{r}}{{Edr}}
\displaystyle \Rightarrow \text{ }\left[ V \right]_{\infty }^{r}\text{=-}\int\limits_{\infty }^{\text{r}}{{\frac{{\text{Kq}}}{{{{\text{r}}^{\text{2}}}}}dr}}
\displaystyle \Rightarrow \text{ }\left[ {{{V}_{r}}-{{V}_{\infty }}} \right]\text{= -Kq}\int\limits_{\infty }^{\text{r}}{{\frac{{dr}}{{{{\text{r}}^{\text{2}}}}}}}
But conventionally \displaystyle {{V}_{\infty }}=0 hence \displaystyle {{\text{V}}_{r}}\text{= -Kq}\left[ {-\frac{1}{r}} \right]_{\infty }^{r}
\displaystyle \Rightarrow {{\text{V}}_{r}}\text{= Kq}\left[ {\frac{1}{r}-\frac{1}{\infty }} \right]
Hence finally we get \displaystyle {{\text{V}}_{r}}\text{= }\frac{{\text{Kq}}}{r}\text{ where r R}
For potential on the the surface of shell put r = R in the final result obtained ,
hence Vsurface= \displaystyle \frac{{Kq}}{R}
For potential inside the shell i.e. for r < R
We know that inside a uniformly charge spherical shell electric field is zero
In the relation \displaystyle E=-\frac{{dV}}{{dr}} if we put E = 0 we get \displaystyle \frac{{dV}}{{dr}}=0 . This shows that V is constant in side the shell. Hence the potential varies out side the shell till the surface where the potential becomes maximum and is given by Vsurface= \displaystyle \frac{{Kq}}{R}. Then inside it remain equal to that on the surface as the electric field vanishes as we enter the shell.
So we conclude that Vinside = Vsurface= \displaystyle \frac{{Kq}}{R}.
Note : Remember that where the electric field is zero the potential may be zero or nonzero but it must be constant .
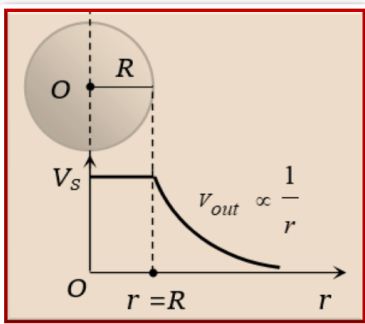
The diagram shows the variation of potential due to a uniformly charged spherical shell.
Potential due to uniformly charged non conducting solid spherical volume
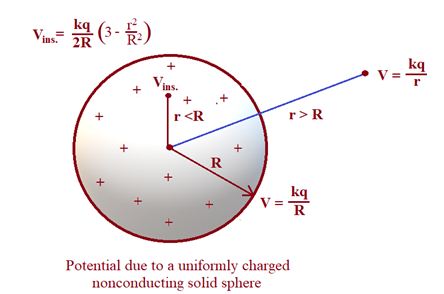
Let the charge in the spherical volume is q and distributed uniformly.
Outside the sphere i.e. For r > R, \displaystyle E=\frac{{kq}}{{{{r}^{2}}}}
Also since E = – \frac{{dV}}{{dr}}
Therefore \displaystyle \Rightarrow dV=-E\times dr
On integration from \displaystyle \infty to r, we get \displaystyle \text{ }\int\limits_{\infty }^{r}{{dV}}\text{= -}\int\limits_{\infty }^{\text{r}}{{Edr}}
\displaystyle \Rightarrow \text{ }\left[ V \right]_{\infty }^{r}\text{=-}\int\limits_{\infty }^{\text{r}}{{\frac{{\text{Kq}}}{{{{\text{r}}^{\text{2}}}}}dr}}
\displaystyle \Rightarrow \text{ }\left[ {{{V}_{r}}-{{V}_{\infty }}} \right]\text{= -Kq}\int\limits_{\infty }^{\text{r}}{{\frac{{dr}}{{{{\text{r}}^{\text{2}}}}}}}
But conventionally \displaystyle {{V}_{\infty }}=0 hence \displaystyle {{\text{V}}_{r}}\text{= -Kq}\left[ {-\frac{1}{r}} \right]_{\infty }^{r}
\displaystyle \Rightarrow {{\text{V}}_{r}}\text{= Kq}\left[ {\frac{1}{r}-\frac{1}{\infty }} \right]
Hence finally we get \displaystyle {{\text{V}}_{r}}\text{= }\frac{{\text{Kq}}}{r}\text{ where r R} (This result is same as that of uniformly charged shell)
For potential on the surface of sphere put r = R in the final result obtained ,
hence Vsurface= \displaystyle \frac{{Kq}}{R} (This result is also same as that of uniformly charged shell)
For potential inside the solid non conducting spherei.e. for r < R
Inside a non conducting solid sphere let the electric field is E
where \displaystyle {{E}_{{in}}}=\frac{{\rho .r}}{{3{{\varepsilon }_{o}}}}=\frac{{Q.r}}{{\frac{4}{3}\pi \text{ }{{\text{R}}^{\text{3}}}\text{.3}{{\varepsilon }_{\text{o}}}}}
\displaystyle \Rightarrow {{E}_{{in}}}=\frac{{Q.r}}{{4\pi {{\varepsilon }_{o}}{{R}^{3}}}}=\frac{{KQ.r}}{{{{R}^{3}}}}
Also we know that outside the non conducting solid sphere the electric field is \displaystyle {{E}_{{out}}}=\frac{{kq}}{{{{r}^{2}}}}
As we know that the potential at any point is the work done to carry a unit positive charge from infinity to that point and is given by the relation \displaystyle \text{ V= -}\int\limits_{\infty }^{\text{r}}{{Edr}} . in this relation E is the electric field between infinity and given point. But in case of solid nonconducting sphere the electric field outside and inside is different so in this case we can define the potential as work done in carrying a unit positive charge from infinity to the surface and then from surface to point inside the sphere.Hence we break the limits of integration as follows
\displaystyle V=-\left[ {\int\limits_{\infty }^{R}{{{{E}_{{out}}}}}dr\text{ + }\int\limits_{\text{R}}^{\text{r}}{{{{\text{E}}_{{in}}}\text{dr}}}} \right]
\displaystyle \Rightarrow V=-\int\limits_{\infty }^{R}{{\frac{{KQ}}{{{{r}^{2}}}}}}\text{ dr }-\text{ }\int\limits_{\text{R}}^{\text{r}}{{\frac{{\text{KQr}}}{{{{\text{R}}^{\text{3}}}}}\text{ dr}}}
\displaystyle \Rightarrow V=-KQ\int\limits_{\infty }^{R}{{\frac{{dr}}{{{{r}^{2}}}}}}\text{ }-\text{ }\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\int\limits_{\text{R}}^{\text{r}}{{\text{r dr}}}
\displaystyle \Rightarrow V=-KQ\left[ {-\frac{1}{r}} \right]_{\infty }^{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\left[ {\frac{{{{r}^{2}}}}{2}} \right]_{R}^{r}
\displaystyle \Rightarrow V=KQ\left[ {\frac{1}{R}-\frac{1}{\infty }} \right]-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\text{ }\left[ {\frac{{{{r}^{2}}}}{2}-\frac{{{{R}^{2}}}}{2}} \right]
\displaystyle \Rightarrow V=\frac{{KQ}}{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}
\displaystyle \Rightarrow V=\frac{{KQ}}{R}-\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{r}^{2}}}}{2}+\frac{{\text{KQ}}}{{{{\text{R}}^{\text{3}}}}}\frac{{{{R}^{2}}}}{2}
\displaystyle \Rightarrow V=\frac{{KQ}}{R}\left[ {1-\frac{{{{r}^{2}}}}{{2{{R}^{2}}}}+\frac{1}{2}} \right]
\displaystyle \Rightarrow V=\frac{{\text{KQ}}}{\text{R}}\left[ {\frac{3}{2}-\frac{{{{r}^{2}}}}{{2{{R}^{2}}}}} \right]
\displaystyle \Rightarrow V=\frac{{\text{KQ}}}{{\text{2R}}}\left[ {3-\frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right]
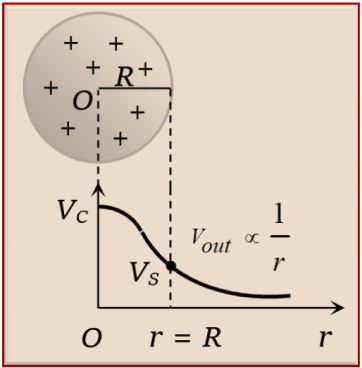
The diagram shows the variation of potential due to a uniformly charged non conducting sphere.
For conducting solid sphere:
(i) (r < R), E = 0, V = \displaystyle \frac{{KQ}}{R}
(ii) (r = R), E = \displaystyle \frac{{KQ}}{{{{R}^{2}}}} , V= \displaystyle \frac{{KQ}}{R}
(iii) (r > R), E = \displaystyle \frac{{KQ}}{{{{r}^{2}}}} , V= \displaystyle \frac{{KQ}}{r}
Illustration
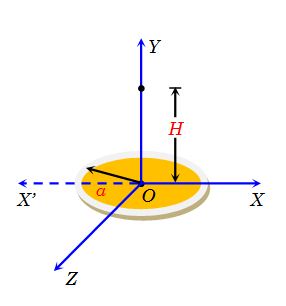
A non-conducting disc of radius ‘a’ and uniform positive surface charge density s is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped along the axis of the disc, from a height H with zero initial velocity. The particle has \frac{q}{m}=\frac{{4{{\varepsilon }_{o}}g}}{\sigma }
(a) Find the value of H the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
Solution
To solve this problem we use the concept of conservation of mechanical energy as the electric field and gravitational field is conservative in nature. Hence mechanical energy at P= Mechanical energy at O.
mgH+q{{V}_{P}}=q{{V}_{0}}
where {{V}_{P}}= Potential at P due to the disc
= {{V}_{P}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left( {2\pi \sigma } \right)\left[ {\sqrt{{{{H}^{2}}+{{a}^{2}}}}-H} \right]
and {{V}_{0}}= Potential at O due to the disc = {{V}_{0}}=\frac{1}{{4\pi {{\varepsilon }_{0}}}}(2\pi \sigma a)
We have taken the reference line X’OX to measure the gravitational potential energy .
mgH = \frac{1}{{4\pi {{\varepsilon }_{0}}}}(2\pi \sigma a) q-\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left( {2\pi \sigma q} \right)\left[ {\sqrt{{{{H}^{2}}+{{a}^{2}}}}-H} \right]
After solving this above equations and using \frac{q}{m}=\frac{{4{{\varepsilon }_{0}}g}}{\sigma } , we get H=\frac{{4a}}{3} .
Note that this problem is solved using force method and work energy theorem.
(b)
Potential energy of particle at height ,
U=\frac{{\sigma q}}{{2{{\varepsilon }_{0}}}}\left[ {\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]+mgy …(i)
Using \frac{q}{m}=\frac{{4{{\varepsilon }_{0}}g}}{\sigma }
U=2mg\left[ {\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]+mgy
U=mg\left[ {2\sqrt{{{{y}^{2}}+{{a}^{2}}}}-y} \right]
For equilibrium , \frac{{dU}}{{dy}}=0
mg\left[ {\frac{{2.2{{y}_{0}}}}{{2\sqrt{{{{y}^{2}}+{{a}^{2}}}}}}-1} \right]= 0
{{y}_{0}}=\frac{a}{{\sqrt{3}}}
As \frac{{{{d}^{2}}U}}{{d{{y}^{2}}}}=mg\left[ {\frac{{2\sqrt{{{{y}^{2}}+{{a}^{2}}}}-2y\times \frac{1}{2}{{{({{y}^{2}}+{{a}^{2}})}}^{{-{1}/{2}\;}}}.2y}}{{({{y}^{2}}+{{a}^{2}})}}} \right]
at y={{y}_{0}}\frac{a}{{\sqrt{3}}} is +ve i.e., \frac{{{{d}^{2}}U}}{{d{{y}^{2}}}}>0
for y={{y}_{0}}=\frac{a}{{\sqrt{3}}}.
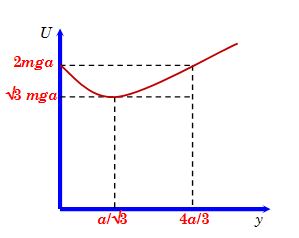
implies that U is minimum at equilibrium.
Umin = \sqrt{3}mga, [Put y=\frac{a}{{\sqrt{3}}} in (i)]
It is interesting at y=\frac{{4a}}{3}, U=2mga
and at y=0, U=2mga.
Potential energy as function of Y is shown in figure.
Potential of concentric conducting spheres: Superposition Principle
Let us consider two spheres of radii r1 and r2 with uniformly distributed charges q1 and q2as shown in the figure .Using the principle of superposition, the potential of the small and large sphere may be written as
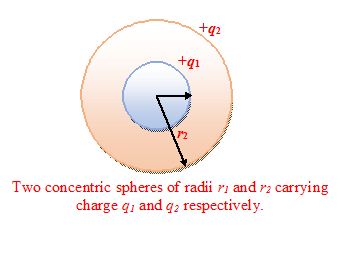
V1 = \frac{{k{{q}_{1}}}}{{{{r}_{1}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}
V2 = \frac{{k{{q}_{1}}}}{{{{r}_{2}}}}\,+\frac{{k{{q}_{2}}}}{{{{r}_{2}}}}
Redistribution of Charge

If two conductors are brought into contact, the charges from one of them will flow over to the other until their potentials become equal. The equality of potential implies that charges on each sphere as shown in figure is proportional to its radius
i.e. \frac{{{{q}_{1}}}}{{{{R}_{1}}}}\,\,=\frac{{{{q}_{2}}}}{{{{R}_{2}}}}
For a uniform surface charge density σ, the total charge q = 4πR2σ,so the above equation becomes
\frac{{{{\sigma }_{1}}}}{{{{\sigma }_{2}}}}\,=\frac{{{{R}_{2}}}}{{{{R}_{1}}}}
The surface charge density of each sphere is inversely proportional to the radius.
Illustration
Given two concentric conducting spheres of radii r and R ( r <R)
The inner surface carries a charge qoand the outer sphere is earthed
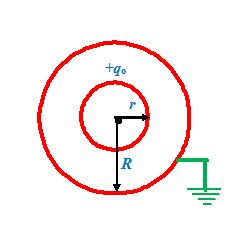
(a) Find the charge on the outer sphere
(b) Find the potential of the inner surface
Solution
(a)
Let q be the final charge on the outer sphere.
Using equation , the potential on the outer sphere is given by
V2 = \frac{{k{{q}_{o}}}}{R}\,+\frac{{kq}}{R}
Since it has been earthed, therefore, V2 = 0
Thus, \frac{{k{{q}_{o}}}}{R}\,+\frac{{kq}}{R} = 0
q = –qo
(b)
The potential of the inner sphere may be obtained using equations
V1 = \frac{{k{{q}_{o}}}}{r}\,-\frac{{k{{q}_{o}}}}{R}
= kqo \left[ {\frac{1}{r}\,-\frac{1}{R}} \right]
Illustration
In the previous example if the outer sphere carries a charge +qo and the inner sphere is earthed, then find
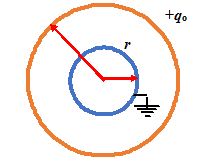
(a) the charge on the inner sphere, and
(b) the potential of the outer sphere.
Solution
(a)
Let q be the charge on the inner sphere.
since it is earthed so its total potential should be zero
hence \frac{{kq}}{r}\,+\frac{{k{{q}_{o}}}}{R}\,=0
Thus q = –qo \frac{r}{R}
(b)
The potential of the outer sphere is given by
V2= \frac{k}{R}\left( {-{{q}_{o}}\frac{r}{R}} \right) + \frac{{k{{q}_{0}}}}{R}
or V2= \frac{{k{{q}_{o}}}}{R}\,\left[ {1\,-\frac{r}{R}} \right]
Practice Questions (Basic Level)
1.
Two infinitely long parallel conducting plates having surface charge densities +s and –s respectively, are separated by a small distance `d’. The medium between the plates is vacuum. If e0 is the dielectric permittivity of vacuum, then the potential difference between the plates is
(a) zero
(b) \displaystyle \frac{{\sigma d}}{{2{{\varepsilon }_{o}}}}
(c) \displaystyle \frac{{\sigma d}}{{{{\varepsilon }_{o}}}} (d) \displaystyle \frac{{2\sigma d}}{{{{\varepsilon }_{o}}}}
Ans (c)
2.
Two spheres of radii r and R carry charges q and Q respectively. When they are connected by a wire, there will be no loss of energy of the system if
(a) qr = QR
(b) qR = Qr
(c) qr2 = QR2
(d) qR2 = Qr2
Ans (b)
3.
In the figure shown, conducting shells A and B have charges Q and 2Q distributed uniformly over A and B .Value of VA – VB is
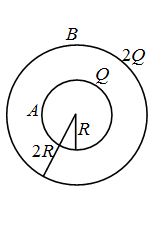
(a) \frac{Q}{{4\pi {{\varepsilon }_{0}}R}}
(b) \frac{Q}{{8\pi {{\varepsilon }_{0}}R}}
(c) \frac{{3Q}}{{4\pi {{\varepsilon }_{0}}R}}
(d) \frac{{3Q}}{{8\pi {{\varepsilon }_{0}}R}}
Ans (b)
4.
A solid conducting sphere of radius 5 cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
(a) 5 V
(b) 10 V
(c) 15 V
(d) zero
Ans (b)
5.
Two concentric conducting shells A and B are of radii R and 2R. A charge q is placed at the centre of shells. Shell B is earthed and a charge q is given to shell A. If charges on outer surface of A and B are QA and QB respectively, then
(a) QA = q, QB = 0 (b) QA = 2q, QB = q
(c) QA = 2q, QB = 0 (d) QA = q, QB = q
Ans (c)
6.
Two spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of
5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surface of spheres A and B is
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 2 : 1
Ans (d)
Practice Questions (JEE Main Level)
1.
Two spheres A and B of radius 4cm and 6cm are given charges of 80mC and 40mC respectively. If they are connected by a fine wire, the amount of charge flowing from one to the other is
(a) 20 \displaystyle \mu C from A to B
(b) 16 \displaystyle \mu C from A to B
(c) 32 \displaystyle \mu C from B to A
(d) 32 \displaystyle \mu C from A to B
Ans (d)
2.
A point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the centre of the shell. The electric potential at the centre of shell will be \frac{1}{{4\pi {{\varepsilon }_{0}}}} times (potential at infinity is zero)
(a) \frac{q}{{2R}}
(b) \frac{{4q}}{{3R}}
(c) \frac{{5q}}{{6R}}
(d) \frac{{2q}}{{3R}}
Ans (c)
3.
A solid hemispherical uniform charged body having charge Q is kept symmetrically along the y-axis as shown in figure. The electric potential at a distance d from the origin along the x-axis at point P will be
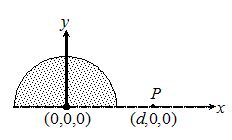
(a) \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{d}
(b) less than \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{d}
(c) more than \frac{1}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}} and less than \frac{2}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}}
(d) more than \frac{2}{{4\pi {{\varepsilon }_{0}}}}\frac{Q}{{{{d}^{{}}}}}
Ans (a)
Practice Questions (JEE Advance Level)
Q.1
A cone made of insulating material has a total charge Q spread uniformly over its sloping surface. Calculate the energy required to bring up a small test charge q from infinity to the apex of the cone. The cone has a slope length L.
(a) \displaystyle \frac{{pQ}}{{8\pi {{\varepsilon }_{o}}L}}
(b) \displaystyle \frac{{qQ}}{{2\pi {{\varepsilon }_{o}}L}}
(c) \displaystyle \frac{{qQ}}{{\pi {{\varepsilon }_{o}}L}}
(d) \displaystyle \frac{{qP}}{{2\pi {{\varepsilon }_{o}}L}}
Ans. (b)
Q.2
Consider the potential at the corner of a uniformly charged cube of dimension L to be directly proportional to \rho {{L}^{2}}, where r is the volume charge density. What is the value of the ratio of the potential at the center to the potential at the corner of the cube?
(a) 4 : 1 (b) 3 : 2 (c) 8 : 1 (d) 2 : 1
Ans. (d)
Q.3
Two concentric shells of radii R and 2R are shown in fig. Initially, a charge q is imparted to the inner shells. Now, key \displaystyle {{K}_{1}} is closed and opened and then key \displaystyle {{K}_{2}} is closed and opened. After the keys \displaystyle {{K}_{1}} and \displaystyle {{K}_{2}} are alternately closed n times each, find the potential difference between the shells. Note that finally key \displaystyle {{K}_{2}} remains closed.
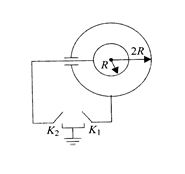
(a) \displaystyle \frac{{-q}}{{5\pi {{\varepsilon }_{0}}{{2}^{{n+5}}}R}}
(b) \displaystyle \frac{q}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
(c) \displaystyle \frac{{-q}}{{\pi {{\varepsilon }_{0}}{{2}^{{n+\theta }}}R}}
(d) \displaystyle \frac{{-q}}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
Ans. (d)
Q.4
Figure shows, in cross section, two solid spheres with uniformly distributed charge throughout their volumes. Each has radius R. Point P lies on a line connecting the centers of the spheres, at radial distance R/2 from the center of sphere 1. If the net electric field at point P is zero, and \displaystyle {{Q}_{1}} is 64 \displaystyle \mu C and \displaystyle {{Q}_{2}} =
8 \displaystyle x\mu C, What is the value of x.
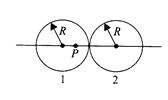
(a) 7 (b) 5 (c) 9 (d) 12
Ans. (c)
Q.5
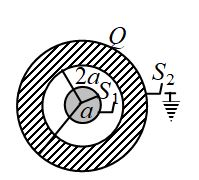
A thick hollow metallic sphere of inner and outer radii 2a and 4a, respectively, encloses a solid concentric metallic sphere of radius ‘a’. these spheres are connected to the earth through switches {{S}_{1}} and {{S}_{2}} as shown in the figure. First, switch {{S}_{1}} is closed and after some time {{S}_{1}} is opened. Then, {{S}_{2}} is closed and after some time {{S}_{2}} is opened. This completes one cycle. Initially, charge Q is given to the outer sphere with both {{S}_{1}} and {{S}_{2}} open. The charge on the inner sphere after n cycles of earthing the inner and outer spheres is
(a) -\frac{Q}{3}
(b) \displaystyle -\frac{Q}{{{{3}^{n}}}}
(c) -{{\left( {\frac{2}{3}} \right)}^{2}}Q
(d) \frac{Q}{{{{3}^{n}}}}
Ans. (b)
Q.6
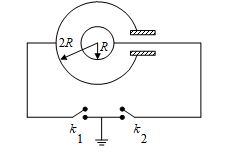
The following figure shows two concentric shells of radii R and 2R. A charge q is initially imparted to the inner shell. After the keys k1 and k2 are alternately closed n times, find the potential difference between the shells.
(a) \frac{q}{{4\pi {{\varepsilon }_{0}}\ R}}
(b) \frac{q}{{4\pi {{\varepsilon }_{0}}\ {{2}^{n}}\ R}}
(c) \frac{q}{{4\pi {{\varepsilon }_{0}}\ {{2}^{{n\ +\ 1}}}\ R}}
(d) \frac{q}{{4\pi {{\varepsilon }_{0}}\ {{2}^{{n\ +\ 2}}}\ R}}
Ans. (c)
Q.7
Figure shows a uniformly charged hemispherical shell. The direction of electric field at point p, that is off-centre (but in the plane of the largest circle of the hemisphere), will be along
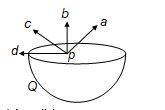
(a) pa (b) pb (c) pc (d) pd
Ans. (b)
Q.8
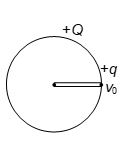
A charge +Q is uniformly distributed in a fixed solid spherical volume of radius R. A particle of charge +q and mass m is projected with velocity from the surface of the spherical volume in small passage made from surface to centre. The minimum value of such that it just reaches the centre of spherical volume (assume no resistance) is
(a) \sqrt{{\frac{{Qq}}{{2\pi {{\in }_{0}}mR}}}}
(b) \sqrt{{\frac{{Qq}}{{\pi {{\in }_{0}}mR}}}}
(c) \sqrt{{\frac{{2Qq}}{{\pi {{\in }_{0}}mR}}}}
(d) \sqrt{{\frac{{Qq}}{{4\pi {{\in }_{0}}mR}}}}
Ans. (d)
Q.9
A charge q is placed at O in the cavity in a spherical uncharged conductor. Point S is outside the conductor. If the charge is displaced from O towards S still remaining within the cavity,
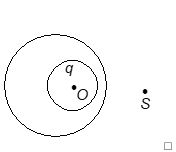
(a) electric field at S will increase
(b) electric field at S will decrease
(c) electric field at S will first increase and the decrease
(d) electric field at S will not change
Ans. (d)
Q.10
A solid sphere having uniform volume charge density r & radius R is shown in fig. A spherical cavity of radius R/2 hollowed out. Find the potential difference between the centre of sphere O & centre of cavity O1
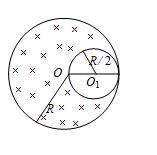
(a) \frac{{\rho {{R}^{2}}}}{{3{{\varepsilon }_{0}}}}
(b) \frac{{\rho {{R}^{2}}}}{{2{{\varepsilon }_{0}}}}
(c) \frac{{\rho {{R}^{2}}}}{{12{{\varepsilon }_{0}}}}
(d) \frac{{\rho {{R}^{2}}}}{{6{{\varepsilon }_{0}}}}
Ans. (c)
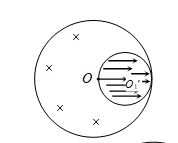
Q.11
The diagram shows three concentric conducting spherical shells having radii R, 2R and 3R. The initial potential of each shell is as mentioned in the figure. If the inner most shell is earth then the charge present on its outer surface would be equal to
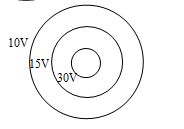
(a) zero
(b) 40\pi {{\varepsilon }_{0}}R
(c) 4\pi {{\varepsilon }_{0}}R
(d) -\pi {{\varepsilon }_{0}}R
Ans. (a)
Q.12
Along solid non-conducting cylinder of radius R has a uniform volume charge density r. Find the potential, difference between the axis and the surface of the cylinder.
(a) \frac{{\rho {{R}^{2}}}}{{7{{\varepsilon }_{0}}}}
(b) \frac{{\rho {{R}^{2}}}}{{{{\varepsilon }_{0}}}}
(c) \frac{{\rho {{R}^{2}}}}{{6{{\varepsilon }_{0}}}}
(d) \frac{{\rho {{R}^{2}}}}{{4{{\varepsilon }_{0}}}}
Ans. (d)
Comprehension Based Question (13 to 15)
A metal sphere of radius a carrying a charge +Q is at the centre of an uncharged thick metal shell of inner radius b and outer radius c, as in fig. Determine the electric field in the following regions:
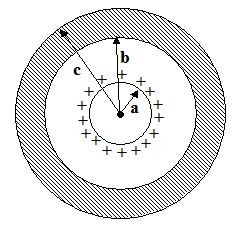
13.
a<r <b.
(i) \frac{{kQ}}{{{{r}^{2}}}}
(ii) \frac{{kQ}}{r}
(iii) \frac{{kQ}}{{{{r}^{6}}}}
(iv) \frac{{kQ}}{{1r}}
Ans (i)
14.
b<r <c.
(i) 0
(ii) 1
(iii) 2
(iv) 3
Ans (i)
15.
r >c.
(i) \frac{{kQ}}{{{{r}^{2}}}}
(ii) \frac{{kQ}}{r}
(iii) \frac{{kQ}}{{{{r}^{6}}}}
(iv) \frac{{kQ}}{{1r}}
Ans (i)
Comprehension Based Question (16 to 17)
A conducting sphere S1of radius r is attached to an insulating handle. Another conducting sphere S2of radius R is mounted on an insulating stand. S2is initially uncharged. S1is given a charge Q, brought into contact with S2, and removed. S1is recharged such that the charge on it is again Q and it is again brought into contact with S2and removed. This procedure is repeated n times.
16.
Find the electrostatic energy of S2after n such contacts with S1.
(a) \frac{{{{Q}^{5}}}}{{3\pi {{\varepsilon }_{o}}R}}{{x}^{5}}{{\left( {\frac{{1-{{x}^{n}}}}{{1-x}}} \right)}^{5}}; x= \frac{R}{{R+r}}
(b) \frac{{{{Q}^{2}}}}{{8\pi {{\varepsilon }_{o}}R}}{{x}^{9}}{{\left( {\frac{{1-{{x}^{n}}}}{{1-x}}} \right)}^{5}} ;x= \frac{R}{{R+r}}
(c) \frac{{{{Q}^{2}}}}{{8\pi {{\varepsilon }_{o}}R}}{{x}^{2}}{{\left( {\frac{{1-{{x}^{n}}}}{{1-x}}} \right)}^{2}}; x= \frac{R}{{R+r}}
(d) \frac{{{{Q}^{2}}}}{{3\pi {{\varepsilon }_{o}}R}}{{x}^{3}}{{\left( {\frac{{1-{{x}^{n}}}}{{1-x}}} \right)}^{3}}; x= \frac{R}{{R+r}}
Ans (c)
17.
What is the limiting value of this energy as n® \displaystyle \infty ?
(a) \frac{{{{Q}^{2}}R}}{{8\pi {{\varepsilon }_{o}}{{r}^{2}}}}
(b) \frac{{{{Q}^{5}}R}}{{8\pi {{\varepsilon }_{o}}{{r}^{5}}}}
(c) \frac{{{{Q}^{3}}R}}{{8\pi {{\varepsilon }_{o}}{{r}^{3}}}}
(d) \frac{{{{Q}^{7}}R}}{{8\pi {{\varepsilon }_{o}}{{r}^{7}}}}
Ans (a)
Comprehension Based Question (18 to 20)
A conducting spherical shell has inner radius R1and outer radius R2with uniform charges densities s C/m2 on the inner and -s C/m2 on the outer
18.
What can you say about the charge within the cavity ?
(a) -2ps
(b) -7ps
(c) -4ps
(d) -7ps
Ans (c)
19.
What can you say about the net charge on the shell ?
(a) -4 \displaystyle \pi \displaystyle \sigma (R_{2}^{2}\,-\,R_{3}^{2})
(b) -5 \displaystyle \pi \displaystyle \sigma (R_{2}^{2}\,-\,R_{1}^{2})
(c) -4 \displaystyle \pi \displaystyle \sigma (R_{2}^{2}\,-\,R_{1}^{2})
(d) -7 \displaystyle \pi \displaystyle \sigma (R_{2}^{2}\,-\,R_{1}^{2})
Ans (c)
20
Find the field outside the shell ?
(a) \frac{{-\sigma \,R_{2}^{2}}}{{{{\varepsilon }_{o}}{{r}^{2}}}}
(b) \frac{{-\sigma \,R_{3}^{5}}}{{{{\varepsilon }_{o}}{{r}^{5}}}}
(c) \frac{{-\sigma \,R_{2}^{7}}}{{{{\varepsilon }_{o}}{{r}^{3}}}}
(d) \frac{{-\sigma \,R_{2}^{5}}}{{{{\varepsilon }_{o}}{{r}^{4}}}}
Ans (a)
Comprehension Based Questions 21 to 24
A metal sphere of radius R1has a charge Q1. It is enclosed by a conducting spherical shell of radius R2that has a charge –Q2. Determine

21.
the potential V1of the inner surface.
(a)k \left( {\frac{{{{Q}_{2}}}}{{{{R}_{2}}}}\,-\frac{{{{Q}_{5}}}}{{{{R}_{5}}}}} \right)
(b)k \left( {\frac{{{{Q}_{2}}}}{{{{R}_{2}}}}\,-\frac{{{{Q}_{3}}}}{{{{R}_{3}}}}} \right)
(c)k \left( {\frac{{{{Q}_{1}}}}{{{{R}_{1}}}}\,-\frac{{{{Q}_{2}}}}{{{{R}_{2}}}}} \right)
(d)k \left( {\frac{{{{Q}_{1}}}}{{{{R}_{1}}}}\,-\frac{{{{Q}_{4}}}}{{{{R}_{4}}}}} \right)
Ans (c)
22.
the potential V1of the outer surface
(a)k \left( {\frac{{{{Q}_{2}}-{{Q}_{2}}}}{{{{R}_{2}}}}} \right)
(b)k \left( {\frac{{{{Q}_{1}}-{{Q}_{2}}}}{{{{R}_{2}}}}} \right)
(c)k \left( {\frac{{{{Q}_{1}}-{{Q}_{4}}}}{{{{R}_{4}}}}} \right)
(d)k \left( {\frac{{{{Q}_{3}}-{{Q}_{3}}}}{{{{R}_{3}}}}} \right)
Ans (b)
23.
the potential difference V1–V2
(a) kQ1 \left( {\frac{9}{{{{R}_{1}}}}\,-\frac{1}{{{{R}_{5}}}}} \right)
(b) kQ1 \left( {\frac{1}{{{{R}_{1}}}}\,-\frac{1}{{{{R}_{2}}}}} \right)
(c) kQ1 \left( {\frac{2}{{{{R}_{1}}}}\,-\frac{1}{{{{R}_{3}}}}} \right)
(d) kQ1 \left( {\frac{3}{{{{R}_{1}}}}\,-\frac{1}{{{{R}_{2}}}}} \right)
Ans (b)
24.
under what condition V1= V2.
(a) Q1= 3
(b) Q1= 4
(c) Q1= 0
(d) Q1= 6
Ans (c)
25.
A system consists of two concentric metallic shells of radii R1and R2with charges q1and q2respectively. Find the total energy of the system if R2>R1.
(a) \frac{1}{{4\pi {{\varepsilon }_{o}}}}\,\left( {\frac{{q_{1}^{6}}}{{2{{R}_{1}}}}\,+\frac{{q_{2}^{6}}}{{2{{R}_{2}}}}\,+\frac{{{{q}_{1}}{{q}_{2}}}}{{{{R}_{3}}}}} \right)
(b) \frac{1}{{4\pi {{\varepsilon }_{o}}}}\,\left( {\frac{{q_{1}^{2}}}{{2{{R}_{1}}}}\,+\frac{{q_{2}^{2}}}{{2{{R}_{2}}}}\,+\frac{{{{q}_{1}}{{q}_{2}}}}{{{{R}_{2}}}}} \right)
(c) \frac{2}{{5\pi {{\varepsilon }_{o}}}}\,\left( {\frac{{q_{1}^{5}}}{{2{{R}_{1}}}}\,+\frac{{q_{2}^{2}}}{{2{{R}_{2}}}}\,+\frac{{{{q}_{1}}{{q}_{2}}}}{{{{R}_{2}}}}} \right)
(d) \frac{1}{{2\pi {{\varepsilon }_{o}}}}\,\left( {\frac{{q_{1}^{2}}}{{2{{R}_{1}}}}\,+\frac{{q_{2}^{2}}}{{2{{R}_{2}}}}\,+\frac{{{{q}_{1}}{{q}_{2}}}}{{{{R}_{2}}}}} \right)
Ans (b)
Comprehension Based Questions (26 and 27)
Three concentric spherical conductors A, B and C are of radii R, 2R and 4R respectively. A &C are shorted and B is uniformly charged (charge = +Q). Find
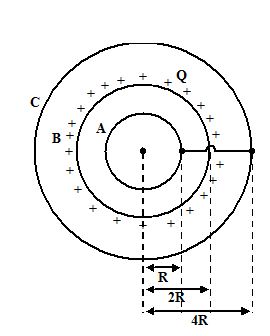
26.
charges on conductors A and C.
(a) \displaystyle {{Q}_{A}}=-Q/8; {{Q}_{C}}=Q/3
(b) {{Q}_{A}}=-Q/3; {{Q}_{C}}=Q/3
(c) \displaystyle {{Q}_{A}}=-Q/4; {{Q}_{C}}=Q/3
(d) \displaystyle {{Q}_{A}}=-Q/2; {{Q}_{C}}=Q/3
Ans (c)
27.
potentials of A and B.
(a) {{V}_{A}}=\frac{Q}{{8\pi {{\varepsilon }_{o}}R}}
(b) {{V}_{A}}=\frac{Q}{{6\pi {{\varepsilon }_{o}}R}}
(c) {{V}_{A}}=\frac{Q}{{16\pi {{\varepsilon }_{o}}R}}
(d) {{V}_{A}}=\frac{Q}{{20\pi {{\varepsilon }_{o}}R}}
Ans (c)
28.
Two concentric shells of radiiR and 2R are shown in figure . Initially a charge q is imparted to the inner shell. After the keys K1&K2 are alternately closed n times each, find the potential difference between the shells. Note that finally the key K2 remains closed.
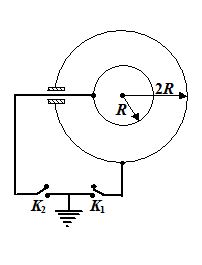
(a) \frac{{-q}}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
(b) \frac{{-q}}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
(c) \frac{{-q}}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
(d) \frac{{-q}}{{4\pi {{\varepsilon }_{0}}{{2}^{{n+1}}}R}}
29.
An electric field is given = 2x – 3y2 N/C. Find the change in potential from the position {{\vec{r}}_{A}}\,=\,\hat{i}\,-\,2\hat{j}\,m to {{\hat{r}}_{B}}=\,2\,\hat{i}\,+\,\hat{j}\,+\,3\,\hat{k} m.
(a) +3V
(b) 2V
(c) +6V
(d) -6V
Ans (c)
